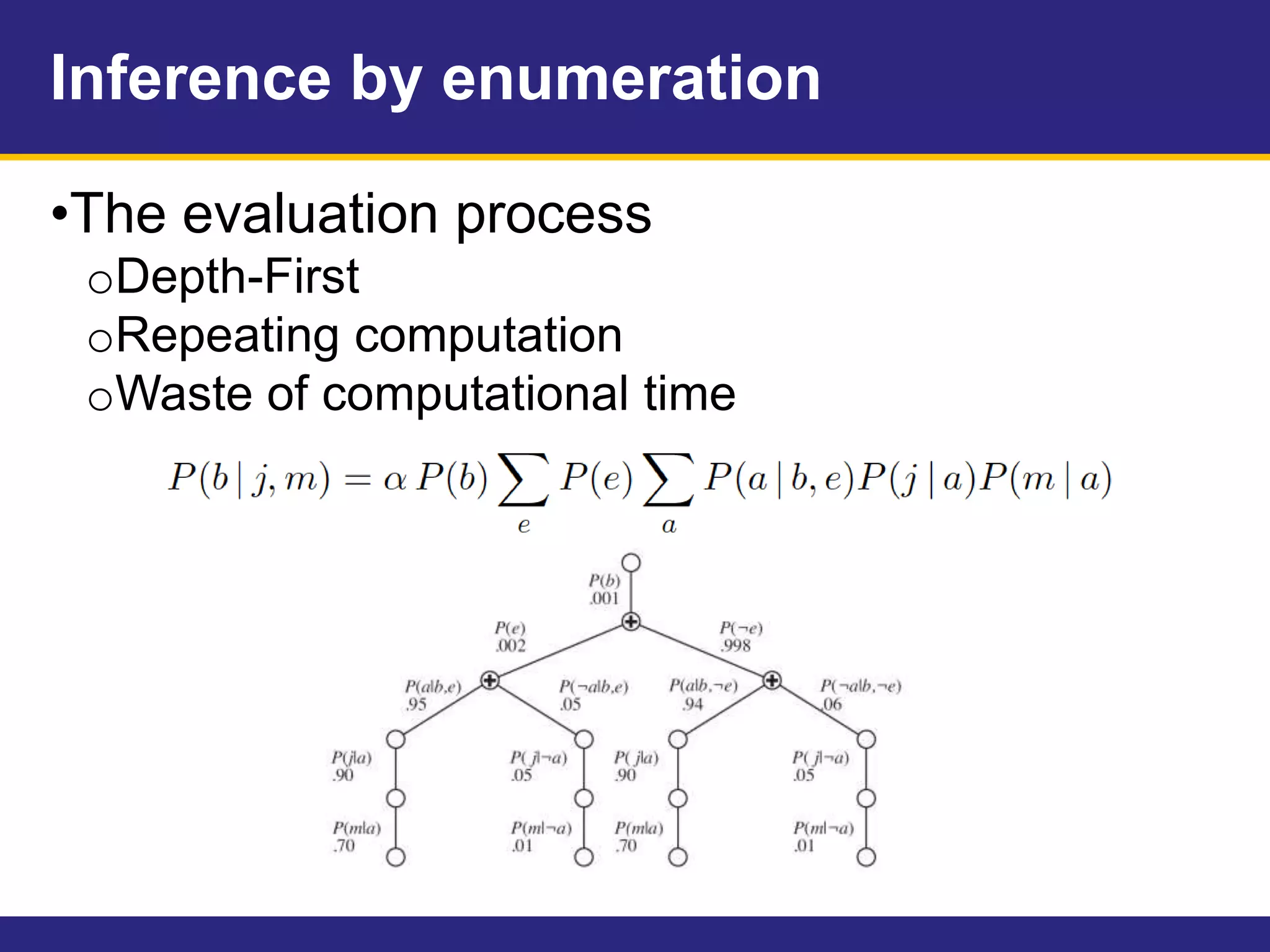
This document provides an overview of Chapter 14 on probabilistic reasoning and Bayesian networks from an artificial intelligence textbook. It introduces Bayesian networks as a way to represent knowledge over uncertain domains using directed graphs. Each node corresponds to a variable and arrows represent conditional dependencies between variables. The document explains how Bayesian networks can encode a joint probability distribution and represent conditional independence relationships. It also discusses techniques for efficiently representing conditional distributions in Bayesian networks, including noisy logical relationships and continuous variables. The chapter covers exact and approximate inference methods for Bayesian networks.

1. PROBABLISTIC RESONING
Artificial Intelligence Modern Approach CH.14
2017.05.19(Fri)
Junya Tanaka(M1)

2. Introduction
•Chapter 13
othe basic elements of probability theory
othe importance of independence and conditional
independence relationships
•This Chapter
oBayesian networks
systematic way to represent such relation- ships explicitly

3. Agenda
•14.1 Representing Knowledge in an Uncertain Domain
•14.2 The Semantics of Bayesian Networks
•14.3 Efficient Representation of Conditional
Distributions
•14.4 Exact Inference in Bayesian Networks
•14.5 Approximate Inference in Bayesian Networks
•14.6 Relational and First-Order Probability Models
•14.7 Other Approaches to Uncertain Reasoning

4. 14.1 Representing Knowledge in an Uncertain Domain
•Bayesian Networks
oA directed graph in which each node is annotated
with quantitative probability information
oDefinition
1. Each node corresponds to a random variable, which
may be discrete or continuous
2. A set of directed links or arrows connects pairs of
nodes. ( If there is an arrow from node X to node Y , X is
said to be a parent of Y. )
3. The graph has no directed cycle.
4. Each node Xi has a conditional probability distribution
P(Xi|Parents(Xi)) that quantifies the effect of the parents
on the node.

5. Simple Example of Bayesian Networks
•The variables Toothache , Cavity, Catch, and
Weather
oWeather is independent of the other variables
oToothache and Catch are conditionally
independent, given Cavity
Cavity is a direct cause of
Toothache and Catch
no direct causal relationship
exists between Toothache
and Catch.

6. Complex Example of Bayesian Networks(1/4)
•The variables Burglary, Earthquake, Alarm,
MaryCalls and JohnCalls
oNew burglar alarm installed at home
oFairly reliable at detecting a burglary
oResponds on occasion to minor earthquakes
oTwo neighbors, John and Mary
oThey call you at work when they hear the alarm
oJohn nearly always calls when he hears the alarm
oBut sometimes confuses the telephone ringing
oMary likes rather loud music and misses the alarm
Give the evidence of who has or has not called,
then estimate the probability of a burglary

7. Complex Example of Bayesian Networks(2/4)
Burglary and Earthquakes
directly affect the probability
of the alarm’s going off
John and Mary call depends
only on the alarm
The network represents our assumptions that they do not perceive
burglaries directly, they do not notice minor earthquakes, and they
do not confer before calling

8. Complex Example of Bayesian Networks(3/4)
•Conditional Probability Table(CPT)
oEach row contains the conditional probability of each node value
oConditioning case is a combination of values for the parent nodes
oEach row must sum to 1
oThe entries represent an exhaustive set of cases for the variable
oFor Boolean variables, The probability of a true value is p, the
probability of false must be 1 – p
oBoolean variable with k Boolean parents contains 2k specifiable
probabilities
oA node with no parents has only one row, representing the prior
probabilities of each possible value of the variable

9. Complex Example of Bayesian Networks(4/4)

10. 14.2 The Semantics of Bayesian Networks
•The two ways to understand the meaning of
Bayesian Networks
oTo see the network as a representation of the joint
probability distribution
To be helpful in understanding how to construct networks,
oTo view it as an encoding of a collection of
conditional independence statements
To be helpful in designing inference procedures

11. Representing the full joint distribution
•Full joint distribution
𝑃 𝑥1 , … . . , 𝑥 𝑛 =
𝑖=1
𝑛
𝑃 𝑥𝑖 𝑥𝑖−1 , … . . , 𝑥1 )
•Ex.
oThe alarm has sounded(a), but neither a burglary(b)
nor an earthquake has occurred(e), and both John(j)
and Mary(m) call
P(j,m,a,¬b,¬e)
= P(j|parents(j))P(m|parents(m)P(a|parents(a))
P(¬b |parents(¬b))P(¬e |parents(¬e))
= P(j|a)P(m|a)P(a|¬b∧¬e)P(¬b)P(¬e)
= 0.90×0.70×0.001×0.999×0.998=0.000628

12. A method for constructing Bayesian networks(1)
•How to construct a GOOD Bayesian network
•Full Joint Distribution
𝑃 𝑥1 , … . . , 𝑥 𝑛 = 𝑖=1
𝑛
𝑃 𝑥𝑖 𝑥𝑖−1 , … . . , 𝑥1 )
𝑃 𝑥1 , … . . , 𝑥 𝑛 = 𝑖=1
𝑛
𝑃 𝑥𝑖 𝑃𝑎𝑟𝑒𝑛𝑡(𝑥𝑖 ))
•Correct representation
oonly if each node is conditionally independent of
its other predecessors in the node ordering, given
its parents
The parents of node Xi should contain all those
nodes in X1,..,Xi−1 that directly influence Xi.

13. A method for constructing Bayesian networks(2)
•Ex
oSuppose we have completed the network in
Figure except for choices of parents for MaryCalls
MaryCalls is certainly influenced by whether there is a
Burglary or an Earthquake, but not directly influenced
Also, given the state of the alarm, whether John calls has
no influence on Mary’s calling
P(MaryCalls | JohnCalls, Alarm, Earthquake, Burglary)
= P(MaryCalls | Alarm)

14. Compactness and node ordering
•Bayesian network can often be far more
compact than the full joint distribution
•It may not be worth the additional complexity
in the network for the small gain in accuracy.
•The correct procedure for adding a node is to
first add the root cause first and then give the
variables that they affect

15. Compactness and node ordering
•We will get a compact Bayesian network only
if we choose the node ordering well
•What happens if we happen to choose the
wrong order?
MaryCalls→JohnCalls
→ Alarm→Burglary
→Earthquake
MaryCalls→JohnCalls
→Earthquake→Burgla
ry→Alarm
Burglary→Earthquake
→Alarm→MaryCalls
→JohnCalls

16. Conditional independence relations in Bayesian networks
•“Numerical” semantics
oFull Joint Distribution
•“Nopological” semantics
oConditional independence relationships by the
graph structure
The “numerical” semantics and the
“topological” semantics are equivalent

17. Conditional independence relations in Bayesian networks
•The topological semantics specifies that each
variable is conditionally independent of its
non-descendants, given its parents
•Ex.
oJohnCalls is independent of Burglary, Earthquake,
and MaryCalls given the value of Alarm

18. Conditional independence relations in Bayesian networks
•A node is conditionally independent of all
other nodes in the network, given its parents,
children, and children’s parents(Markov
blanket)
•Ex.
•Burglary is independent of JohnCalls and
MaryCalls, given Alarm and Earthquake

19. Conditional independence relations in Bayesian networks
A node X is
conditionally
independent of its non-
descendants (e.g., the
Zijs) given its parents
(the Uis shown in the
gray area)
A node X is
conditionally
independent of all other
nodes in the network
given its Markov
blanket (the gray area).

20. 14.3 Efficient Representation of Conditional Distributions
•CPT cannot handle large number or continuous
value varibles.
•Relationships between parents and children are
usually describable by some proper canonical
distribution.
•Use the deterministic nodes to demonstrate
relationship.
oValues are specified by some function.
onondeterminism(no uncertainty)
oEx. X = f(parents(X))
oCan be logical
NorthAmerica ↔ Canada ∨ US ∨ Mexico
oOr numercial
Water level = inflow + precipitation – outflow - evaporation

21. 14.3 Efficient Representation of Conditional Distributions
•Uncertain relationships can be characterized
by noisy logical relationships.
•Ex. noisy-OR relation.
oLogical OR with probability
oEx. Cold ∨ Flu ∨ Malaria → Fever
In the real world, catching a cold sometimes does not
induce fever.
There is some probability of catching a cold and having a
fever.

22. 14.3 Efficient Representation of Conditional Distributions
•Noisy-OR
oAll possible causes are listed. (the missing can be
covered by leak node)
oCompute probability from the inhibition probability

23. 14.3 Efficient Representation of Conditional Distributions
•Suppose these individual inhibition
probabilities are as follows:
Variable depends
on k parents can
be described
using O(k)
parameters
instead of O(2k)

24. Bayesian nets with continuous variables
•Many real world problems involve continuous
quantities
oInfinite number of possible values
oImpossible to specify conditional probabilities
•Discretization
odividing up the possible values into a fixed set of
intervals
oIt’s often results in a considerable loss of accuracy
and very large CPTs
To define standard families of probability density
functions(Gaussian,etc )

25. Bayesian nets with continuous variables
•Hybrid Bayesian network
oHave both discrete and continuous variables
oTwo new kinds of distributions
Continuous variable given discrete or continuous parents
Discrete variable given continuous parents
•Example
Customer buys some fruit depending
on its cost which depends in turn on
the size of the harvest and whether
the government’s subsidy scheme is
operating.
D C
C
D

26. Hybrid Bayesian network
•P(Cost|Harvest , Subsidy )
oSubsidy(Discrete)
P(Cost|Harvest,subsidy) and P(Cost|Harvest,¬subsidy)
oHarvest(Continuous)
How the distribution over the cost c depends on the
continuous value h of Harvest
Specify the parameters of the cost distribution as a
function of h
D C
C
D

27. Hybrid Bayesian network
•The linear Gaussian distribution
oMost common choice
oThe child has a Gaussian distribution
GD has μ varies linearly with the value of the parent
GD has standard deviation σ that is fixed
oTwo distributions, subsidy and ¬subsidy, with
different parameters at, bt, σt, af , bf , and σf:

28. Hybrid Bayesian network
•A : P(Cost|Harvest,subsidy)
•B : P(Cost|Harvest,¬subsidy)
•C : P (c | h)
oaveraging over the two possible values of Subsidy
oassuming that each has prior probability 0.5

29. Other Distribution
•Distributions for discrete variables with
continuous parents
•Consider the Buys node
oCustomer will buy if the cost is low
oCustomer will not buy if it is high
o the probability of buying varies smoothly
•Probit Distribution
•Logit Distribution
D C
C
D

30. 14.4 Exact Inference in Bayesian Networks
•The task for probabilistic inference system
ogiven some observed event
some assignment of values to a set of evidence
variables
ocompute the posterior probability distribution for a
set of query variables
•Ex(In the burglary network)
oobserve JohnCalls = true and MaryCalls = true
othe probability that a burglary has occurred:

31. Inference by enumeration
•Chapter 13
oAny conditional probability can be computed by
summing terms from the full joint distribution
X denotes the query variable;
E denotes the set of evidence variables E1, . . . ,Em, and
e is a particular observed event;
Y will denotes the nonevidence, nonquery variables Y1, .
. . , Yl (called the hidden variables)
The complete set of variables is X={X}∪ E ∪Y
the posterior probability distribution P(X | e).

32. Inference by enumeration
•P(X | e) can be answered using a Bayesian
network by computing sums of products of
conditional probabilities from the network
•Ex
oConsider the query P(Burglary | JohnCalls
=true,MaryCalls =true)
oThe hidden variables for this query are
Earthquake and Alarm

33. Inference by enumeration
oFor simplicity, we do this just for Burglary =true:
O(n2 𝑛
)
O(2 𝑛
)
the P(b) term is a constant and can be moved
outside the summations over a and e
The chance of a burglary, given calls from both neighbors, is about 28%

34. Inference by enumeration
•The evaluation process
oDepth-First
oRepeating computation
oWaste of computational time

35. The variable elimination algorithm
•The enumeration algorithm can be improved
by eliminate repeated calculations
•The idea is :
odo the calculation once and save the results for
later use(dynamic programming)

36. Clustering algorithms
•Not Clustering of ML
•Join tree algorithms
oThe time can be reduced
oThe basic idea of clustering is to join individual
nodes of the network to form cluster
oNodes in such a way that the resulting network is
a polytree

37. 14.5 Approximate Inference in Bayesian Networks
•Difficult to calculate multiply connected
networks
•It is essential to consider approximate
inference methods
•Monte Carlo algorithms
oRandomized sampling algorithms
otwo families of algorithms: direct sampling and
Markov chain sampling
oApply to the computation of posterior probabilities

38. Direct sampling methods
•Primitive element is the generation of
samples from a known probability distribution
•Sampling process for Bayesian networks
generates events from a network
•In topological order
•The probability distribution is conditioned on
the values already assigned to the variable’s
parents

39. Direct sampling methods
•Ex. Assuming an ordering
[Cloudy, Sprinkler, Rain, WetGrass]
1.Sample from P(Cloudy)
P(Cloudy) = <0.5, 0.5>
Cloudy = True

40. Direct sampling methods
•Ex. Assuming an ordering
[Cloudy, Sprinkler, Rain, WetGrass]
2.Sample from P(Sprinkler|Cloudy=true)
P(S|C=true) = <0.1, 0.9>
Sprinkler = false

41. Direct sampling methods
•Ex. Assuming an ordering
[Cloudy, Sprinkler, Rain, WetGrass]
3.Sample from P(Rain|Cloudy=true)
P(R|C=true) = <0.8, 0.2>
Rain = true

42. Direct sampling methods
•Ex. Assuming an ordering
[Cloudy, Sprinkler, Rain, WetGrass]
4.Sample from P(W|S=false, R=true)
P(W|S=false, R=true) = <0.9, 0.1>
WetGrass = true
•In this case, the event
[Cloudy, Sprinkler, Rain, WetGrass]
= [true, false, true, true]

43. Rejection sampling in Bayesian networks
•Producing samples from a hard-to-sample
distribution used an easy-to-sample
distribution
•1. It generates samples from the prior
distribution
•2. It rejects all those that do not match the
evidence
•3. The estimate P(X =x | e) is obtained by
counting how often X =x occurs in the
remaining samples

44. Rejection sampling in Bayesian networks
•Ex. Estimate P(Rain|Sprinkler=true) using
100 samples.
o27 samples have Sprinkler = true
The rest 73s are false → ignore those 73.
oOf the 27 remaining samples.
n(Rain=true) : n(Rain=false) = 8 : 19
oP^(Rain|Sprinkler=true)
= <8/27 : 19/27>
= <0.296 : 0.704>
•Rejection sampling is consistent for large
number of sampling

45. Likelihood weighting
•Sample only nonevidence variables, and
weight each sample by the likelihood it
accords to the evidence

46. Likelihood weighting
•Ex. P(Rain|Cloudy = true, WetGrass = true)
oEvidence variable : Cloudy, WetGrass
•Order = Cloudy, Sprinkler, Rain, WetGrass
•Cloudy (evid.)
oUpdate weight w
ow ← w x P(Cloudy = true) = 0.5
•Sprinkler(non evid.)
oSample
oP(Sprinkler|Cloudy=true) = <0.1, 0.9>
oSprinkler = false
•Rain(non evid.)
oSample
oP(Rain|Cloudy=true) = <0.8, 0.2>
oRain = true
•WetGrass(evid.)
oUpdate weight w
ow ← w x P(WetGrass=true|Sprinkler = false, Rain=true) =
0.5x0.9 = 0.45

47. Inference by Markov chain simulation
•Markov chain
oRandom process in state space, each state is
independent of the previous state(memoryless)
•Monte Carlo
oA class of randomized algorithm whose running
time is deterministic
•Markov chain Monte Carlo(MCMC)
oA random sampling algorithm sampling each
event(state) by randomly moving to the new one

48. Gibbs sampling in Bayesian networks
•A randomized sampling method based on
MCMC
•Suitable for Bayesian network
•Start with an arbitrary state with fixed
evidence variables at their observed state
•Randomly sampling a value for one of the
nonevidence variables Xi
oThe sampling is done conditioned on the current
values of the variables in the Markov blanket of Xi
oMarkov blanket = parents, children, children’s
parents

49. Gibbs sampling in Bayesian networks
•Example
•P(Rain|Sprinkler = true, WetGrass = true)
oEvidence var = Sprinkler, WetGrass
oNonevidence var = Rain, Cloudy
o1.Arbitrarily initialize Rain and Cloudy(say true,
false)
[Cloudy, Sprinkler, Rain, WetGrass] = [T,T,F,T]

50. Gibbs sampling in Bayesian networks
•Ex. Sampling
P(Rain|Sprinkler = true, WetGrass = true)
oCurrent state
[Cloudy, Sprinkler, Rain, WetGrass] = [T,T,F,T]
o2.Sample Cloudy
Its Markov’s blanket consists of Sprinkler, Rain.
Sample from P(Cloudy|Sprinkler=true, Rain=false)
Suppose we get false
Move to the next state with changed Cloudy
[Cloudy, Sprinkler, Rain, WetGrass] = [F,T,F,T]

51. Gibbs sampling in Bayesian networks
•Ex. Sampling
P(Rain|Sprinkler = true, WetGrass = true)
oCurrent state
[Cloudy, Sprinkler, Rain, WetGrass] = [F,T,F,T]
o3.Sample Rain
Its Markov’s blanket consists of Sprinkler, Cloudy,
WetGrass.
Sample from
P(Rain|Sprinkler=true, Cloudy=false, WetGrass = true)
Suppose we get true.
Move to the next state with changed Cloudy
[Cloudy, Sprinkler, Rain, WetGrass] = [F,T,T,T]

52. Gibbs sampling in Bayesian networks
•Ex. Sampling
P(Rain|Sprinkler = true, WetGrass = true)
oCurrent state
o4. Keep doing 2,3 until reaching the number of
sampling
Suppose we need to do 80 samplings.
Get 20 states where Rain = true
60 where Rain = False
P(Rain|Sprinkler = true, WetGrass = true)
= α<20,60>
= <0.25, 0.75>

53. Gibbs sampling
•Gibbs sampling works at large number of
sampling saying that it has reached its
stationary distribution.(Converge)
oTime spent at each state equals to proportional to
its posterior distribution.
•Main computation problem
oHard to tell if it has converged.
oIf Markov’s blanket is large, consume a lot of
computational time

54. 14.6 Relational and First-order Probability models
•Bayesian networks are essentially
propositional logic.
•The set of random variables is fixed and finite.
•However, if the number becomes large,
intractable.
•Need another method to represent the model

55. 14.6 Relational and First-order Probability models
•The set of first-order models is infinite.
•Use database semantics instead called
“Relational Probability models”.
•Make unique names assumption and assume
domain closure.
•Like first-order logic
oConstant
oFunction
oPredicate symbols
•Assume type signature

56. 14.6 Relational and First-order Probability models
•Example
oAn online book retailer would like to provide
overall evaluations of products based on
recommendations received from its customers
oFor a single customer C1, recommending a single
book B1, the Bayes net might look like :

57. 14.6 Relational and First-order Probability models
•Example
oWith two customers and two books, the Bayes net
looks like
oFor larger numbers of books and customers, it
becomes completely impractical to specify the
network by hand

58. 14.6 Relational and First-order Probability models
•We would like to say something like
oA customer’s recommendation for a book depends
on the customer’s honesty and kindness and the
book’s quality
•This section develops a language that lets us
say exactly this, and a lot more besides

59. Relational probability model
•Ex. Book recommendation
“Customer” C recommends some book B by giving
score based on its “Quality” but score might vary
according to his “Kindness” and “Honesty”
•Type signature = Customer, Book
•Function and predicates
oHonest : Customer → {true, false}
oKindness : Customer → {1, 2, 3, 4, 5}
oQuality : Book → {1, 2, 3 ,4 5}
oRecommendation : Customer x Book → {1, 2, 3, 4, 5}
•Constants are whatever customer and book
names appear in the data.
oEx. “Harry Potter and the ……..” or “John”

60. Relational probability model
•Ex. Book recommendation(Cont.)
“Customer” C recommends some book B by giving
score based on its “Quality” but score might vary
according to his “Kindness” and “Honesty”
•Finally, assign dependencies that govern the
variables.
oHonest(c) ~ <0.99, 0.01>
oKindness(c) ~ <0.1, 0.1, 0.2, 0.3, 0.3>
oQuality(b) ~ <0.05, 0.2, 0.4, 0.2, 0.15>
oRecommendation(c, b) ~ RecCPT(Honest(c),
Kindness(c), Quality(b))
oRecCPT is separately defined conditional distribution
with 2 x 5 x 5 = 50 rows with 5 entries(Score 1-5)

61. Relational probability model
•We can redefine a model by specifying the
model to follow another defined rules.
•This is called “context-specific independence”
•For example, dishonest customers ignore quality
when giving a recommendation.
The criteria has no concerned → criteria functions
become independent.
Recommendation(c, b) is independent of Kindness(c),
Quality(b) when Honest(c) = false.
Recommendation(c, b) ~
if Honest(c) then
HonestRecCPT(Kindness(c), Quality(b))
else <0.4, 0.1, 0.0, 0.1, 0.4>

62. Relational probability model
•Inference in RPMs
•The idea is similar to propositionalization.
•Unrolling
oCollect evidences, query, and constant symbols
oConstruct equivalent Bayesian network
oApply any inference methods previously mentioned
•Problem
oValue of everything in the network must be known
beforehand.
oEx. Author = {A1, A2}, Author(Book1) = ?
Haven’t specified Author(Book1), but must be A1 or A2.
Uncertainty in the value of Author(Book1) is called relational
uncertainty

63. Open-universe probability models
•Database semantics is good at the setting where
every relevant objects exist and can be identified
unambiguously.
•Real-world setting is not in that form.
oEx. Father’s wife, aunt’s sister, grandma’s daughter → my
mom
•Bayesian network
oGenerate each possible world, event by event in order by
assignment of value to a variable.
•RPM
oGenerate entire sets of events defined by the possible
instantiations of the logical variables.
•OUPM
oAdd object to the world under construction.
oNot assigning value, but create the very existence of the
object

64. 14.7 Other Approaches to Uncertain Reasoning
•Rule-based methods for uncertain reasoning
•Emerged from logical inference
•Require 3 desirable properties
oLocality : If A B, we can conclude B given
evidence A without worrying about any other rules.
But in probabilistic systems, we need to consider all
evidence.
oDetachment : If we can derive B, we can use it
without caring how it was derived.
oTruth-functionality : truth value of complex
sentences can be computed from the truth of the
components.
Probability combination does not work this way

65. Representing ignorance: Dempster–Shafer theory
•Designed to deal with
ouncertainty : nothing is certain
oignorance : no idea whether evidence is real
•Not compute the probability of a proposition.
•Compute the probability that the evidence
supports the proposition.
•Belief function Bel(X): Show how trustable the
evidence is for event X.

66. Representing ignorance: Dempster–Shafer theory
Ex. Pick a coin from a magician’s pocket.
Rather not believe that the coin is fair.
•Bel(Head) = 0 x 0.5
•Bel(¬Head) = 0
Ex. A coin made by expert with 90% certainty
that the coin is fair.
•Bel(Head) = 0.9 x 0.5 = 0.45
•Bel(¬Head) = 0.9 x (1 – 0.5) = 0.45
•1 – 0.45 – 0.45 = 0.1 ← gap not accounted
for by the evidence

67. Representing ignorance: Dempster–Shafer theory
•Assign masses to sets of possible event.
•Masses is added to 1 over all possible event.
•Bel(A) is sum of masses for all events that are
subsets of A, including A.
•B(A) + B(¬A) is at most 1.
•Interval between Bel(A) and 1 – Bel(¬A) is
bounding the probability of A.

68. Representing vagueness: Fuzzy sets and fuzzy logic
•Fuzzy set theory : specifying how well an
object satisfies a vague description.
oEx.170 is tall or short?
Available answer = {tall, short}
Reality = “sort of…”
•Everything doesn’t need to be on extreme left
or right, somewhere in the middle is
acceptable, no sharp boundary.
oEx. Tall or Short are called fuzzy predicates.
oTall(X) ranges between 0 and 1.
•Fuzzy set theory ≠ uncertain reasoning
method.

69. Representing vagueness: Fuzzy sets and fuzzy logic
•Fuzzy logic : method for reasoning with
logical expression describing membership in
fuzzy sets.
•Suppose T(Tall(A)) = 0.6, T(Heavy(A)) = 0.4
oT(Tall(A) ∧ Heavy(A)) = 0.4
o“A is not that tall and heavy.”
T(A ∧ B) = min(T(A), T(B)
T(A ∨ B) = max(T(A), T(B)
T(¬A) = 1 – T(A)

70. Representing vagueness: Fuzzy sets and fuzzy logic
•Fuzzy control
oa methodology for constructing control systems
where the mapping between real-valued input and
output parameters is represented by fuzzy rules.
oSuccessful in commercial products such as
automatic transmission, video cameras, etc.
oLikely to become successful because of small rule
bases, no chaining inferences, etc.

71. Summary
oA Bayesian network is a directed acyclic graph
whose nodes correspond to random variables;
each node has a conditional distribution for the
node, given its parents.
oBayesian networks provide a concise way to
represent conditional independence
relationships in the domain.
oA Bayesian network specifies a full joint
distribution; each joint entry is defined as the
product of the corresponding entries in the local
conditional distributions. A Bayesian network is
often exponentially smaller than an explicitly
enumerated joint distribution

72. Summary
oMany conditional distributions can be represented
compactly by canonical families of distributions.
Hybrid Bayesian networks, which include both
discrete and continuous variables, use a variety of
canonical distributions.
oInference in Bayesian networks means computing
the probability distribution of a set of query
variables, given a set of evidence variables. Exact
inference algorithms, such as variable
elimination, evaluate sums of products of
conditional probabilities as efficiently as possible

73. Summary
oStochastic approximation techniques such as
likelihood weighting and MCMC can give reasonable
estimates of the true posterior probabilities in a
network and can cope with much larger networks than
can exact algorithms.
oProbability theory can be combined with
representational ideas from first-order logic to produce
very powerful systems for reasoning under uncertainty.
Relational probability models (RPMs) include
representational restrictions that guarantee a well-
defined probability distribution that can be expressed
as an equivalent Bayesian network. Open-universe
probability models handle existence and identity
uncertainty, defining probability distributions over the
infinite space of first-order possible worlds.

74. Summary
oVarious alternative systems for reasoning under
uncertainty have been suggested. Generally
speaking, truth-functional systems are not well
suited for such reasoning.