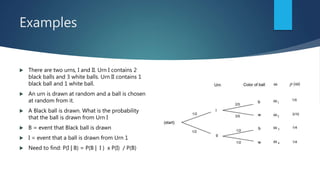
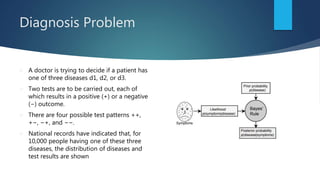
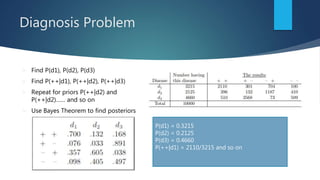
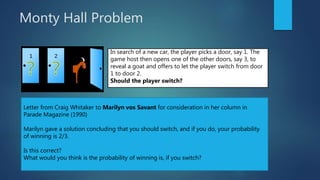
This document provides an introduction to probability and statistical concepts using R. It defines key terms like random variables, sample space, events, and probability. It discusses definitions of probability, conditional probability, independent and dependent events. It provides examples of calculating probabilities for things like coin tosses, dice rolls, and card draws. It also introduces Bayes' theorem and provides examples of how to calculate conditional probabilities using this approach. Finally, it discusses how naive Bayes classification works in machine learning by applying Bayes' theorem.

1. Statistical Analysis-2
USING R

2. Introduction to
probability
2.1. Basic probability : Definition and examples
2.2. Conditional probability
2.3. Bayes theorem
2.4 Applications of Bayes theorem in real life
scenario

3. Definitions
 A variable is a symbol (A, B, x, y, etc.) that can take on any of a specified set of values.
 When the value of a variable is the outcome of a statistical experiment, that variable is a random
variable.
 Sample Space = set of all possible outcomes of an experiment.
 Event = subset of the Sample Space. (example coin toss)
 Generally, statisticians use a capital letter to represent a random variable and a lower-case letter,
to represent one of its values. For example,
 X represents the random variable X.
 P(X) represents the probability of X.
 P(X = x) refers to the probability that the random variable X is equal to a particular value,
denoted by x. As an example, P(X = 1) refers to the probability that the random variable X is
equal to 1.

4. Definitions : Statistical Experiment
All statistical
experiments
have three
things in
common:
The experiment can have more than one possible outcome.
Each possible outcome can be specified in advance.
The outcome of the experiment depends on chance.

5. Probability of an Event

6. Probability of an event
Throwing two dice
Event(e): Sum of the two dice is 6.
What is the probability of the above
event?
List all possible outcomes.
There are 36 of them.
P(e) = 5/36

7. Interpreting Probability
If P(A) equals zero, event A will almost definitely not occur.
If P(A) is close to zero, there is only a small chance that event A will occur.
If P(A) equals 0.5, there is a 50-50 chance that event A will occur.
If P(A) is close to one, there is a strong chance that event A will occur.
If P(A) equals one, event A will almost definitely occur.

8. Probability: definitions
P(E) >= 0 and P(E) <= 1
If E1, E2, E3, E4…. En are outcomes of a statistical experiment,
P(Ei) >= 0 and P(Ei) <= 1 and P(E1) + P(E2) + …. P(En) = 1
Two events are mutually exclusive or disjoint if they cannot occur at the
same time.

9. Probability: definitions
The probability that Events A and B both occur is the probability of
the intersection of A and B.
The probability of the intersection of Events A and B is denoted by P(A ∩ B).

10. Probability: definitions
The probability that Events A or B occur is the probability of the union of
A and B.
The probability of the union of Events A and B is denoted by P(A ∪ B) .

11. Probability: definitions
The complement of an event is the event not occurring.
The probability that Event A will not occur is denoted by P(A').
P(A) = 1 - P(A')

12. Probability: definitions
If the occurrence of Event A changes the probability of Event B,
then Events A and B are dependent.
If the occurrence of Event A does not change the probability of
Event B, then Events A and B are independent.

13. Probability: definitions
The probability that Event A occurs, given that Event B has
occurred, is called a conditional probability.
The conditional probability of Event A, given Event B, is denoted by
the symbol P(A|B).

14. Independent Events
Independence Probability of event A occurring does NOT depend on probability of
event B occurring.
 Fair Coin in tossed 2 times.
 Event A = head in first toss.
 Event B = head in 2nd toss.
 Probability of a Head in the 2nd toss is ½, irrespective of whether there was a head
or a tail in the first toss.
 A and B are Independent
 Event A = It will rain in Bangalore today, Event B = It will rain in Hosur today. (Are
they independent?)

15. Independent Events
PROBABILITY OF A AND B
When two events are independent, the probability of both occurring is the
product of the probabilities of the individual events. More formally, if events A
and B are independent, then the probability of both A and B occurring is: P(A
and B) = P(A) x P(B)
Draw a card from a deck of cards, put it back, and then draw another card. What
is the probability that the first card is a heart and the second card is black? Since
there are 52 cards in a deck and 13 of them are hearts, the probability that the
first card is a heart is 13/52 = 1/4. Since there are 26 black cards in the deck, the
probability that the second card is black is 26/52 = 1/2. The probability of both
events occurring is therefore 1/4 x 1/2 = 1/8

16. Independent Events
PROBABILITY OF A OR B
If Events A and B are independent, the probability that either Event A or Event B occurs is: P(A
or B) = P(A) + P(B) - P(A and B)
when we say "A or B occurs" we include three possibilities:
 A occurs and B does not occur
 B occurs and A does not occur
 Both A and B occur
If you throw a six-sided die and then flip a coin, what is the probability that you will get either
a 6 on the die or a head on the coin flip (or both)? Using the formula,
P(6 or head) = P(6) + P(head) - P(6 and head)
= (1/6) + (1/2) - (1/6)(1/2)
= 7/12

17. Conditional Probability
PROBABILITY OF A GIVEN B : P(A|B)
If Events A and B are independent, P(A|B) = P(A)
When A and B are NOT independent
What is the probability that two cards drawn at random from a deck of playing cards
will both be aces?
Can you simply multiply 4/52 x 4/52 = 1/169? (incorrect because A and B are NOT
independent)
P(ace on second draw | an ace on the first draw)
Since after an ace is drawn on the first draw, there are 3 aces out of 51 total cards left.
This means that the probability that one of these aces will be drawn is 3/51 = 1/17.

18. Conditional Probability
PROBABILITY OF A GIVEN B : P(A|B)
If Events A and B are independent, P(A|B) = P(A)
What is the probability that two cards drawn at random from a deck of playing cards
will both be aces?
P(ace on second draw | an ace on the first draw)
Since after an ace is drawn on the first draw, there are 3 aces out of 51 total cards left.
This means that the probability that one of these aces will be drawn is 3/51 = 1/17.
If Events A and B are not independent, then P(A and B) = P(A) x P(B|A).
Applying this to the problem of two aces, the probability of drawing two aces from a
deck is 4/52 x 3/51 = 1/221.

19. Examples
 Experiment: rolling a dice once.
 Outcome: X
 Event : F is the event {X = 6}, and E is the event {X > 4}.
 Distribution function m(ω)=1/6 for ω = 1, 2,..., 6. Thus, P(F)=1/6.
 Now suppose that the dice is rolled and we are told that the event E
has occurred.
 This leaves only two possible outcomes: 5 and 6. In the absence of
any other information, we would still regard these outcomes to be
equally likely, so the probability of F becomes 1/2, making
P(F|E)=1/2.

20. Examples
 There are two urns, I and II. Urn I contains 2 black balls and
3 white balls. Urn II contains 1 black ball and 1 white ball.
 An urn is drawn at random and a ball is chosen at random
from it.
 A Black ball is drawn. What is the probability that the ball is
drawn from Urn I
 B = event that Black ball is drawn
 I = event that a ball is drawn from Urn 1
 Need to find: P(I | B) = P(B | I ) x P(I) / P(B)

21. Examples
 There are two urns, I and II. Urn I contains 2
black balls and 3 white balls. Urn II contains 1
black ball and 1 white ball.
 An urn is drawn at random and a ball is chosen
at random from it.
 A Black ball is drawn. What is the probability
that the ball is drawn from Urn I
 B = event that Black ball is drawn
 I = event that a ball is drawn from Urn 1
 Need to find: P(I | B) = P(B | I ) x P(I) / P(B)

22. Joint Distribution Functions
 In a group of 60 people, we have the numbers of
who do or do not smoke and do or do not have
cancer.
Let Ω be the sample space consisting of these 60 people.
A person is chosen at random from the group.
Let C(ω) = 1 if this person has cancer and 0 if not, and
S(ω) = 1 if this person smokes and 0 if not.
Joint Distribution: {C, S} =
{cancer & smoking ;
cancer & non-smoking;
no-cancer &smoking;
no-cancer & non-smoking}

23. Marginal Distribution Functions
The distributions of the individual random variables are called
marginal distributions
Probability (Cancer) = 10/60
Probability(No Cancer) = 50/60
Probability (Smoking) = 47/60
Probability(NotSmoking) = 13/60

24. Checking Independence
Are the random variables S and C Independent?
Condition for Independence
P(C = 1 and S = 1) = 3/60
P(C = 1) x P(S = 1) = 10/60 x 13 /60
Therefore C and S are NOT independent
E and F are independent if and only if
P(E ) > 0 and P(F ) > 0 AND

25. Bayes Theorem
Bayes’ Theorem is a way of finding a probability when we know certain other
probabilities.
P(H |E) = P(H) P(E|H) / P(E)
How often H happens given that E happens, written P(H|E),
When we know:
How often E happens given that H happens, written P(E|H)and
How likely H is on its own, written P(H) and
How likely E is on its own, written P(E)

26. Bayes Theorem
Two events
P(H |E) = P(H) P(E|H) / P(E)
More than two events

27. Bayes Theorem: Example 1
Hunter (a cat) says she is itchy.
There is a test for Allergy to Cats, but this test is not always right:
For cats that really do have the allergy, the test says "Yes" 80%of the time
For cats that do not have the allergy, the test says "Yes" 10% of the time
("false positive")
If 1% of the population have the allergy, and Hunter's test says "Yes", what
are the chances that Hunter really has the allergy?

28. Bayes Theorem: Example 1
For cats that really do have the allergy, the test says "Yes" 80% of the time.
P(+|allergy) = 0.8
For cats that do not have the allergy, the test says "Yes" 10% of the time.
P(+|no allergy) = 0.1
If 1% of the population have the allergy,
P(allergy) = 0.01
Hunter's test says "Yes", what are the chances that Hunter really has the
allergy?
To find: P(allergy | +)

29. Bayes Theorem:
Example 1
P(Yes|allergy) = 0.8
P(Yes|no allergy) = 0.1
P(allergy) = 0.01
To find: P(allergy | +)
P(Yes) = P(Yes | allergy) x P(allergy) +
P(Yes|noallergy)xP(noallergy)

30. Bayes Theorem: Example 1
P(Yes|allergy) = 0.8
P(Yes|no allergy) = 0.1
P(allergy) = 0.01
To find: P(allergy | +)
Answer?
Try to create a probability tree.

31. Bayes Theorem: Example 2
If dangerous fires are rare (1%) but smoke is fairly common (10%) due to barbecues,
and 90% of dangerous fires make smoke then "Probability of dangerous Fire when
there is Smoke"
P(Fire) means how often there is fire (1%)
P(Smoke) means how often we see smoke (10%)
P(Fire|Smoke) means how often there is fire when we can see smoke
P(Smoke|Fire) means how often we can see smoke when there is fire (90%)
So the formula kind of tells us "forwards/posterior" P(Fire|Smoke) when we know
"backwards" P(Smoke|Fire) and prior P(Smoke)

32. Bayes Theorem: Example 2
P(Fire) means how often there is fire (1%)
P(Smoke) means how often we see smoke
(10%)
P(Smoke|Fire) means how often we can
see smoke when there is fire (90%)
P(Fire|Smoke) means how often there is fire
when we can see smoke

33. Bayes Theorem: Example 3
Suppose that a test for using a particular drug is 99% sensitive and
99% specific. That is, the test will produce 99% true positive results for drug
users and 99% true negative results for non-drug users.
Suppose that 0.5% of people are users of the drug. What is
the probability that a randomly selected individual with a positive test is a
drug user?

34. Bayes Theorem: Example 3
Formulate the problem in terms of probabilities.
Draw the probability tree.
Answer?

35. Bayes Theorem: Example 3

36. Bayes Theorem: Example 3

37. Bayes Theorem: Example 4
Pam put in 15 paintings, 4% of her works have won First Prize.
Pia put in 5 paintings, 6% of her works have won First Prize.
Pablo put in 10 paintings, 3% of his works have won First Prize.
What is the chance that Pam will win First Prize?

38. Bayes Theorem: Example 4

39. Bayes Theorem Uses
 Bayes probabilities are particularly appropriate for medical diagnosis.
 A doctor is anxious to know which of several diseases a patient might
have.
 She collects evidence in the form of the outcomes of certain tests.
 From statistical studies the doctor can find the prior probabilities of the
various diseases before the tests, and the probabilities for specific test
outcomes, given a particular disease.
 What the doctor wants to know is the posterior probability for the
particular disease, given the outcomes of the tests

40. Naïve Bayes in Machine Learning
 In machine learning one is often interested in selecting the best hypothesis
(h) given data (d).
 In a classification problem, our hypothesis (h) may be the class to assign
for a new data instance (d).
 One of the easiest ways of selecting the most probable hypothesis given
the data that we have that we can use as our prior knowledge about the
problem. Bayes’ Theorem provides a way that we can calculate the
probability of a hypothesis given our prior knowledge.

41. Naïve Bayes in Machine Learning
Bayes’ Theorem is stated as:
P(h|d) = (P(d|h) * P(h)) / P(d)
 P(h|d) is the probability of hypothesis h given the data d. This is called the posterior
probability.
 P(d|h) is the probability of data d given that the hypothesis h was true.
 P(h) is the probability of hypothesis h being true (regardless of the data). This is called
the prior probability of h.
 P(d) is the probability of the data (regardless of the hypothesis).
After calculating the posterior probability for a number of different hypotheses, you can
select the hypothesis with the highest probability. This is the maximum probable hypothesis
and may formally be called the maximum a posteriori(MAP) hypothesis.

42. Diagnosis Problem
 A doctor is trying to decide if a patient has
one of three diseases d1, d2, or d3.
 Two tests are to be carried out, each of
which results in a positive (+) or a negative
(−) outcome.
 There are four possible test patterns ++,
+−, −+, and −−.
 National records have indicated that, for
10,000 people having one of these three
diseases, the distribution of diseases and
test results are shown

43. Diagnosis Problem
 Find P(d1), P(d2), P(d3)
 Find P(++|d1), P(++|d2), P(++|d3)
 Repeat for priors P(++|d2) and
P(++|d2)…… and so on
 Use Bayes Theorem to find posteriors
P(d1) = 0.3215
P(d2) = 0.2125
P(d3) = 0.4660
P(++|d1) = 2110/3215 and so on

44. Monty Hall Problem
In search of a new car, the player picks a door, say 1. The
game host then opens one of the other doors, say 3, to
reveal a goat and offers to let the player switch from door
1 to door 2.
Should the player switch?
Letter from Craig Whitaker to Marilyn vos Savant for consideration in her column in
Parade Magazine (1990)
Marilyn gave a solution concluding that you should switch, and if you do, your probability
of winning is 2/3.
Is this correct?
What would you think is the probability of winning is, if you switch?

45. Monty Hall Problem

46. Birthday Problem
If there are 25 people in a room, what is the probability that at least two of them share the same
birthday.
25/365 = 0.068
What is the probability that no two people have the same birthday. Once we know this probability, we
can simply subtract it from 1 to find the probability that two people share a birthday.

47. Birthday Problem
If we choose two people at random, what is the probability that they do not share a birthday?
Let's define P2 as the probability that the second person drawn does not share a birthday with
the person drawn previously.
P2 = 364/365
Let's define P3 as the probability that the third person drawn does not share a birthday with the persons
drawn previously.
P3 = 363/365
P4 = 362/365, P5 = 361/365, and so on up to P25 = 341/365.

48. Birthday Problem
If we choose two people at random, what is the probability that they do not share a birthday?
Let's define P2 as the probability that the second person drawn does not share a birthday with
the person drawn previously.
P2 = 364/365
Let's define P3 as the probability that the third person drawn does not share a birthday with the persons
drawn previously.
P3 = 363/365
P4 = 362/365, P5 = 361/365, and so on up to P25 = 341/365.

49. Birthday Problem
 In order for there to be no matches, the second person must not match any previous
person and the third person must not match any previous person, and the fourth person must
not match any previous person, etc.
 Since P(A and B) = P(A)P(B), all we have to do is multiply P2, P3, P4 ...P25 together.
 P(no two bday’s matching) = P2 x P3 x P4 x …. P25 = 0.431
 Therefore the probability of at least one match is 0.569.

50. Problem Set
Exercise 1
1% of people have a certain genetic defect.
90% of tests for the gene detect the defect (true positives).
9.6% of the tests are false positives.
If a person gets a positive test result, what are the odds they actually have the genetic
defect?

51. Problem Set
Exercise 2
Given the following statistics, what is the probability that a woman has cancer if she has a
positive mammogram result?
 One percent of women over 50 have breast cancer.
 Ninety percent of women who have breast cancer test positive on mammograms.
 Eight percent of women will have false positives.

52. Problem Set
Solution 1.1
 The first step into solving Bayes’ theorem problems is to assign letters to events:
 A = chance of having the faulty gene. That was given in the question as 1%. That also means
the probability of not having the gene (~A) is 99%.
 X = A positive test result.

53. Problem Set
Solution 1.2
 P(A|X) = Probability of having the gene given a positive test result.
 P(X|A) = Chance of a positive test result given that the person actually has the gene. That was
given in the question as 90%.
 p(X|~A) = Chance of a positive test if the person doesn’t have the gene. That was given in the
question as 9.6%
 Now we have all of the information we need to put into the equation:
P(A|X) = (.9 * .01) / (.9 * .01 + .096 * .99) = 0.0865 (8.65%).
 The probability of having the faulty gene on the test is 8.65%.

54. Problem Set
Solution 2
 Assign events to A or X. You want to know what a woman’s probability of having cancer is,
given a positive mammogram. For this problem, actually having cancer is A and a positive test
result is X.
 List out the parts of the equation (this makes it easier to work the actual equation):
P(A)=0.01
P(~A)=0.99
P(X|A)=0.9
P(X|~A)=0.08
 Insert the parts into the equation and solve.
(0.9 * 0.01) / ((0.9 * 0.01) + (0.08 * 0.99) = 0.10.

55. Problem Set