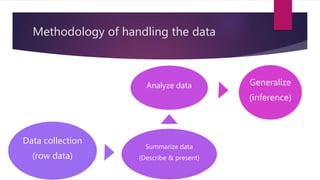
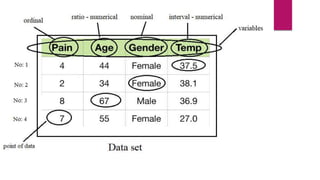
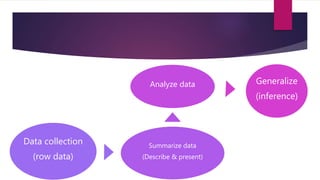
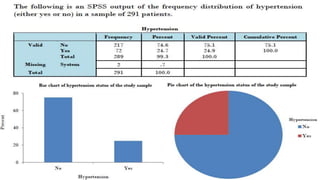
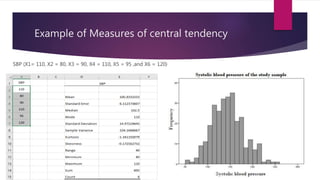
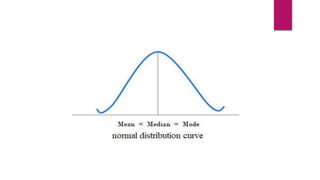
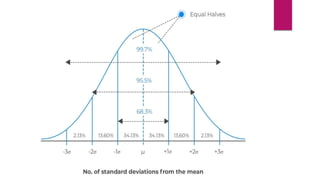
The document provides an overview of basic statistics, covering concepts such as data collection, organization, analysis, and the distinction between statistics and parameters. It outlines the types of variables, descriptive statistics for both categorical and continuous data, as well as measures of central tendency and dispersion. Additionally, it discusses inferential statistics, including confidence intervals, hypothesis testing, and examining associations between variables.

1. Statistics - Basic concepts
BY
Ibrahim Abdelmonaem
ZMRS TEAM

2. Statistics
what
when
why

3. What … ?
 Statistics is the science concerned with collection, organization, analysis,
interpretation and presentation of data.
 Why … ??
 When … ??

4. Methodology of handling the data
Data collection
(row data)
Summarize data
(Describe & present)
Analyze data Generalize
(inference)

5. Data Vs Information
 Data: row materials (individual values)
 Information: processed data – management of data
 Variable !!!

6. Variable …
 Any thing can change and can be measured and observed
Types of variables – four types:
 Nominal variables (dichotomous / multi nominal)
 Ordinal variables
 Interval variables
 Ratio variables

8. Data
 Quantitative Data (numerical)
 Qualitative Data (categorical)

9. Data collection
(row data)
Summarize data
(Describe & present)
Analyze data Generalize
(inference)

10. Statistic Vs Parameter
 Statistic
 A statistical value that is calculated from all the values in a sample.
 Latin letters are used for the sample statistics
 Parameter
 A statistical value that is calculated from all the values in a whole population.
 Greek letters are used for the population parameters

12. Descriptive statistics
 Descriptive statistics are the techniques used to summarize and describe the main features
of a sample (measure variability).
 The type of descriptive statistics depends on types of variables
 Descriptive statistics for categorical (nominal / ordinal) variables
 Descriptive statistics for continuous variables

13. Describing categorical (nominal / ordinal) variables
 Frequency distribution table
 Graph presentation
 Bar chart
 Pie chart

15. Describing continuous variables
 Summary values:
 Measures of central tendency
 Mean
 Median
 mode
 Measure of dispersion
 Range
 Inter quartile range (IQR)
 variance
 Standard deviation (SD)
 Graph presentation
 Histogram
 Normal distribution curve (Gaussian curve)

16. Example of Measures of central tendency
SBP (X1= 110, X2 = 80, X3 = 90, X4 = 110, X5 = 95 ,and X6 = 120)

17. Inferential statistics
 Inferential statistics is a type of statistics that is used to draw conclusions on a population used
data that was collected on a sample.
 A statistical step performed to generalize the results found in the study to the population under
consideration.
 There are two main types of inferential statistics:
 Confidence interval.
 Hypothesis testing (p-value).

18. Probability and Hypothesis
 Inferential statistics is highly related to probability distributions.
 Probability distribution is a statistical function describing the probability of all possible values
of a continuous variable.
 The most frequently used distribution is the normal distribution.

21. Examining the associations between two variables
 Absolute risk
 A measure to indicate the probability of an event to occur.
 Relative risk / Risk ratio
 A measure to assess the association between two different groups.
 Risk difference / Attributable risk
 A measure to indicate the difference in the risks between the exposure groups.
 Difference in means

22. THANK YOU