The document discusses image enhancement techniques in digital image processing, focusing on spatial domain methods. It covers various approaches like contrast stretching, histogram processing, and spatial filtering, explaining mechanisms such as pixel manipulation and the application of filters. Additionally, it distinguishes between linear and non-linear filtering techniques and their roles in enhancing image quality.

1. DIGITAL IMAGE PROCESSING
Spatial Domain
&
Spatial Filtering
November 30, 2016 1

2. INTRODUCTION TO IMAGE
ENHANCEMENT
Enhancement is to process an image so that the result is more suitable than
the original image for a specific application
Two approaches use for image enhancement:
Spatial domain: Refer to the image plane itself. Direct manipulation of pixels in
an image
Frequency Domain: Based on modifying the Fourier Transform of an image
November 30, 2016 2

3. 3
GOOD IMAGES
• For human visual
– The visual evaluation of image quality is a highly
subjective process.
– It is hard to standardize the definition of a good
image.
• For machine perception
– The evaluation task is easier.
– A good image is one which gives the best machine
recognition results.
• A certain amount of trial and error usually is
required before a particular image enhancement
approach is selected.

4. 4
SPATIAL DOMAIN
• Procedures that operate
directly on pixels.
g(x,y) = T[f(x,y)]g(x,y) = T[f(x,y)]
where
– f(x,y)f(x,y) is the input image
– g(x,y)g(x,y) is the processed image
– TT is an operator on ff defined
over some neighborhood of
(x,y)(x,y)

5. 5
MASK/FILTER
• Neighborhood of a point (x,y) can
be defined by using a
square/rectangular (common used)
or circular subimage area centered
at (x,y)
• The center of the subimage is
moved from pixel to pixel starting
at the top of the corner
•
(x,y)

6. 6
POINT PROCESSING
• Neighborhood = 1x1 pixel
• gg depends on only the value of ff at (x,y)(x,y)
• TT = gray level (or intensity or mapping)
transformation function
s = T(r)s = T(r)
• Where
– rr = gray level of f(x,y)f(x,y)
– ss = gray level of g(x,y)g(x,y)

7. GRAY LEVEL IMAGE TRANSFORMATION
The value of pixels before and after processing are denoted by r and s,
s = T(r), Where T is Transformation
Basic types of function used for image enhancement:
Linear: Negative and identity transformations
Logarithm: Log and inverse log transformations
Power-low: n-th power and n-th root transformations
November 30, 2016 7

8. LOG AND POWER
TRANSFORMATIONS
Log transformations:
s = clog(1+r) where, c is a constant, r>=0
Power-low transformations:
s=crγ,
where c and γ are positive constants
Gamma Corrections:
The exponent of the power law equation is referred to
as gamma. The process used to correct this power law
response phenomena is called gamma correction.
November 30, 2016 8

9. IMAGE ENHANCEMENT IN THE SPATIAL DOMAIN
(CONTRAST STRETCHING)
November 30, 2016 9
 Contrast stretching is piecewise-linear transformation
function.
 to increase the dynamic range of the gray levels in the
image being processed
T(r)
(r2, s2)
L/2
L/4
3L/4
(r1, s1)
L-1L/2 3L/4
L-1
L/40
Input gray level, r
outputgraylevel,s

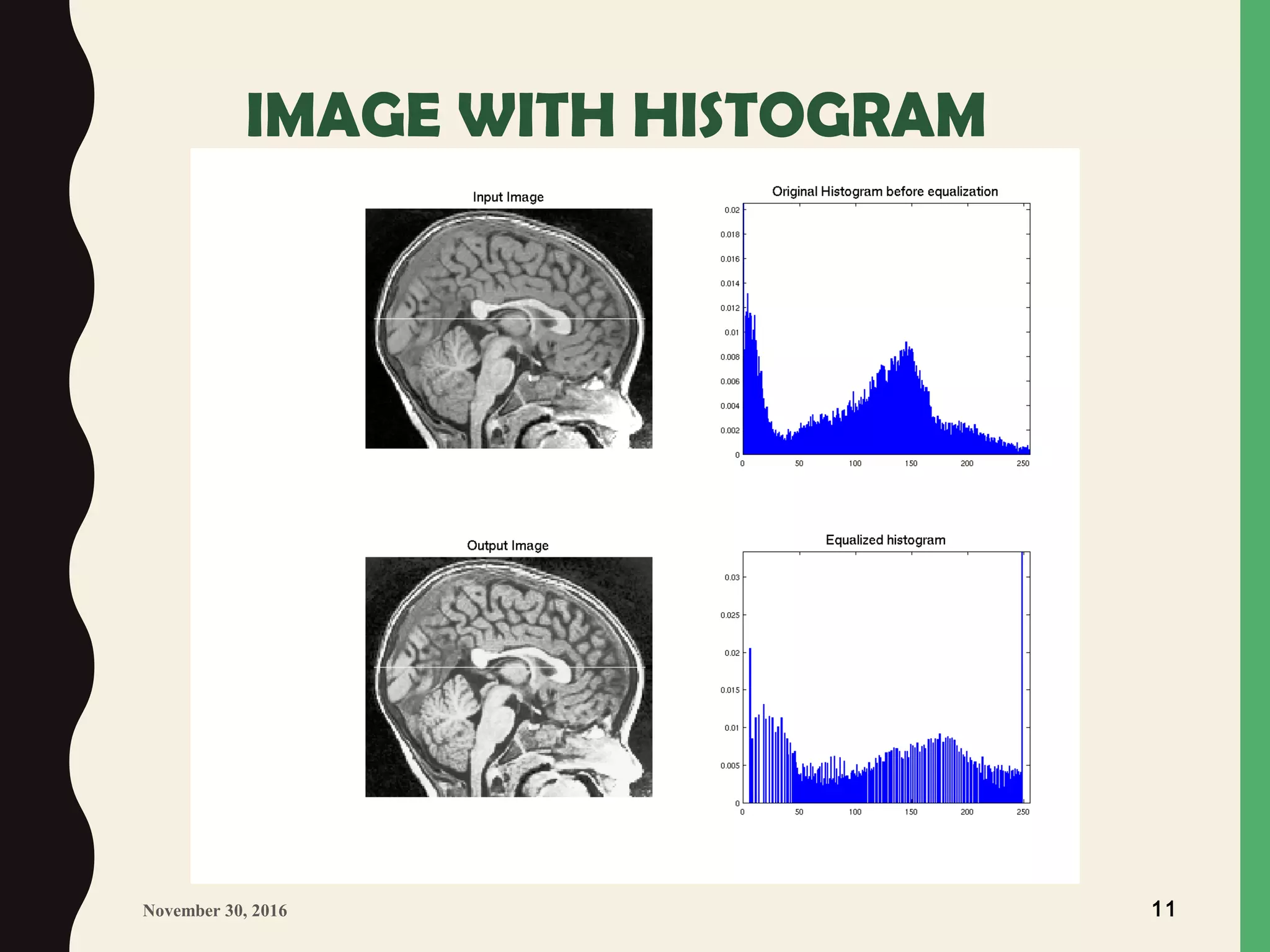
10. IMAGE ENHANCEMENT IN THE
SPATIAL DOMAIN
(HISTOGRAM PROCESSING)
Intensity distribution in the image
The histogram functions count the number
of elements within a range and display each range
as a rectangular bin. The height (or length
when using rose) of the bins represents the
number of values that fall within each range.
for (int i=0;i<width;i++){
for (int j=0;j<height;j++){
int x = pixels[i][j];
histData[x] =histData[x]+1;
}
}
November 30, 2016 10

11. IMAGE WITH HISTOGRAM
November 30, 2016 11

12. HISTOGRAM EQUALIZATION
The probability of occurrence of gray
level rk in an image is approximated
by,
Where k =0,1,2,---L-1; n is the total
number of pixels, nk is the number of
pixels that have gray level rk.
A plot pr(rk) vs. rk is called histogram
The transformation (mapping) sk is
called histogram equalization
∑ ∑= =
===
k
j
k
j
j
jrkk
n
n
rPrTs
0 0
)()(
November 30, 2016 12
( ) k
k
n
P r
n
=

13. HISTOGRAM EQUALIZATION ALGORITHM
1. Calculate Histogram
loop over i ROWS of input image
loop over j COLS of input image
k = input_image[i][j]
hist[k] = hist[k] + 1
end loop over j
end loop over i
2. calculate the sum of hist
loop over i gray levels
sum = sum + hist[i]
sum_of_hist[i] = sum
end loop over i
November 30, 2016 13
 3. Transform input image to
output image
area = area of image (ROWS x COLS)
Dm = number of gray levels in output
image
loop over i ROWS
loop over j COLS
k = input_image[i][j]
out_image[i][j] = (Dm/area) x sum_of_hist[k]
end loop over j
end loop over i

14. COMPARISON OF IMAGE:
BEFORE AND AFTER HISTOGRAM EQUALIZATION
November 30, 2016 14
Make low bright region
to higher bright
Reduce the number of
gray level

15. IMAGE ENHANCEMENT IN THE
SPATIAL DOMAIN:
November 30, 2016 15
Local Enhancement:
Enhancement of image in a particular area to reduce
noise.
Image ArithmaticImage Arithmatic
Image subtraction, addition, multiplication, division
g (x, y) = f (x, y) – h (x, y)
g (x, y) = f (x, y) + h (x, y)

16. BASICS OF SPATIAL FILTERING
Some neighborhood operations work with the values of the
image pixels in the neighborhood and the corresponding values
of a sub-image that has a same dimensions as the neighborhood.
This sub-image is called filter, mask, kernel, template or
window.
The values in a filter sub-image are referred to as coefficients,
rather than pixels
Filtering operations that are performed directly on the pixels of
an image is called spatial Filtering.
November 30, 2016 16

17. BASICS OF SPATIAL FILTERING
November 30, 2016 17
(0,0)
Mask
Image f(x,y)
y
x
W(-1,-1) W(-1,0) W(-1,1)
W(1,0)W(1,-1)
W(0,-1) W(0,0) W(0,1)
W(1,1)
f(x+1,y+1)f(x+1,y)f(x+1,y-1)
f(x,y-1)
f(x,y+1)
f(x-1,y+1)f(x-1,y)f(x-1,y-1)
f(x,y)
Pixels of image
section under mask
Mask coefficients

18. BASICS OF SPATIAL FILTERING
Moving the filter mask from point to point in an image At
each point (x,y), the response of the filter at that point is
calculated using a predefined relationship
The response is given by a sum of products of the filter
coefficients and the corresponding image pixels in the area
spanned by the filter mask.
Limitation near boundary:
to limit the excursions of the center of the mask to be at a
distance no less than (n-1)/2
padding by 0 or constant gray level, then stripped
November 30, 2016 18

19. SMOOTHING SPATIAL FILTERS
November 30, 2016 19
Smoothing Linear Filter:
The output (response) of a smoothing, linear spatial filter is simply the average
of the pixels contained in the neighborhood of the filter mask. These filters
sometimes are called averaging filters or low pass filters.
1
9
×
11
11
1
1
1
11
1
16
×
12
42
1
2
1
12
3x3 smoothing filter masks

20. SMOOTHING SPATIAL FILTERS
November 30, 2016 20
Non-Linear Spatial Filter:
The nonlinear spatial filter whose response is based on ordering the pixels
contained in the image area encompassed by the filter and then replacing the
value of the center pixel with the value determined by the ranking result. The
best known filter is median filters.
Max Filters: use to find the brightest point
Min Filters:use to find the darkest point

21. SHARPENING SPATIAL FILTERS
Sharpening is to highlight fine detail in an image
First-order derivative: of an one dimensional function, f(x)
Second-Order derivative
November 30, 2016 21
( 1) ( )
f
f x f x
x
∂
= + −
∂
2
2
( 1) ( 1) 2 ( )
f
f x f x f x
x
∂
= + + − −
∂

22. EXAMPLE OF FIRST AND SECOND
ORDER DERIVATIVES
November 30, 2016 22
1st
derivative
2nd
derivative
05 023 145
f(x-1) f(x) f(x+1)
0 6 0 0 0
-1, -1, -1, -1, -1, 0, 0, 6, -6, 0
7 7 ..
-1, 0, 0, 0, 0, 1, 0, 6, -12, 6
First order derivative produce thick edge
2nd
order derivative produce much finer one and strong response at
isolated point

23. Thank You