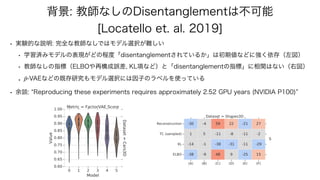
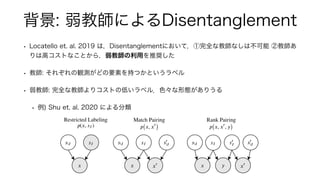
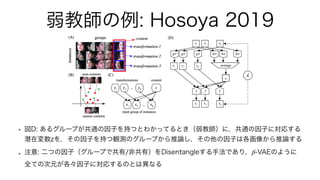
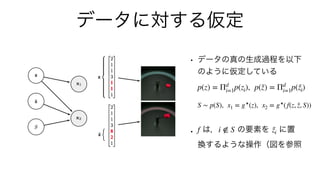
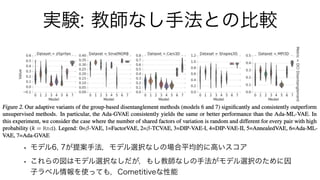
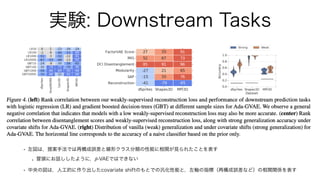
1. The document presents a method for deep learning using variational autoencoders that model the relationship between pairs of data points (x1, x2). 2. It introduces variables to represent latent vectors z and z~ that are used to generate x1 and x2, as well as a subset S of dimensions that relate x1 and x2. 3. The method works by training an encoder qφ(z|x) to approximate a prior p(z) and maximize the likelihood of generating x1 and x2 from their respective latent representations, while minimizing the KL divergence between the encoder and prior.

1. DEEP LEARNING JP
[DL Papers]
http://deeplearning.jp/

3. z = [z1, . . . , zd]T
̂z = [ ̂z1, . . . , ̂zd]T
̂z
f π i zi = fi( ̂zπ(i))
z

4. P(z) f
p(z) = p( f(z)) z, f(z)
i, j
∂fi(u)
∂uj
for a . e . u ∈ supp(z)
P( f(z)) p( f(z)) p(z)
β
q(z) =
∫
q(z|x)pdata(x)dx
q(z) p(z) p( f(z))
p(z)

5. β

7. β

8. (x1, x2)
(x1, x2) k ≥ 1

9. (x1, x2)
(x1, x2) k ≥ 1

10. p(z) = Πd
i=1p(zi), p(˜z) = Πd
i=1p(˜zi)
S ∼ p(S), x1 = g⋆
(z), x2 = g⋆
(f(z, ˜z, S))
f i ∉ S ˜zi

11. (x1, x2)
(x1, x2) k ≥ 1

12. (x1, x2) ∼ p(x1, x2) =
∫ ∫ ∫
p(x1, x2, z, ˜z, S)dzd˜zdS
|S| = k
S, S′ ∼ p(S) P(S ∩ S′ = {i}) > 0,∀i ∈ [d]
p( ̂zi) q(x1 | ̂z) p( ̂S)
q( ̂z) =
∫
q( ̂z|x1)p(x1)dx

13. S x1, x2
zi∈S zi∉S ̂zi∈T ̂zi∉T
(x1, x2) ∼ p(x1, x2 |S)
S

14. p (zi |x1) = p (zi |x2) ∀i ∈ S
p (zi |x1) ≠ p (zi |x2) ∀i ∈ ¯S
k S
k
k S

15. max
ϕ,θ
𝔼(x1,x2)
𝔼˜qϕ( ̂z|x1)
log (pθ (x1 | ̂z))
+𝔼˜qϕ( ̂z|x2)
log (pθ (x2 | ̂z))
−βDKL (˜qϕ ( ̂z||x1)|p( ̂z))
−βDKL (˜qϕ ( ̂z||x2)|p( ̂z))
˜qϕ ( ̂zi |x1) = a (qϕ ( ̂zi |x1), qϕ ( ̂zi |x2)) ∀i ∈ ̂S
˜qϕ ( ̂zi |x1) = qϕ ( ̂zi |x1)
(x1, x2)
i ∈ ̂S qϕ ( ̂zi |x1), qϕ ( ̂zi |x2) a
δi = DKL (qϕ ( ̂zi |x1) ∥qϕ ( ̂zi |x2))

16. (x1, x2)
(x1, x2) k ≥ 1

17. β β

20. β

22. k (x1, x2)
(x1, x2)