This document summarizes a research paper on semi-supervised learning with deep generative models. It presents the key formulas and derivations used in variational autoencoders (VAEs) and their extension to semi-supervised models. The proposed semi-supervised model has two lower bounds - one for labeled data that maximizes the likelihood of inputs given labels, and one for unlabeled data that maximizes the likelihood based on inferred labels. Experimental results show the model achieves better classification accuracy compared to supervised models as the number of labeled samples increases.

1. Semi-supervised Learning with Deep Generative Model By Kingma
mabonki0725
()1 論文読会
October 30, 2017

2. Variational Formula
General Variational Formula From PRML Ÿ10
log pθ(x) = −
∫
qϕ(z) log
pθ(z|x)
qϕ(z)
dz +
∫
qϕ(z) log
pθ(z, x)
qϕ(z)
dz (1)
log pθ(x) = KL(qϕ(z)||pθ(z|x)) +
∫
qϕ(z) log
pθ(z, x)
qϕ(z)
dz (2)
log pθ(x) = KL(qϕ(z)||pθ(z|x)) − L (3)
log pθ(x) ≥ −L (4)
2 / 16

3. VAE
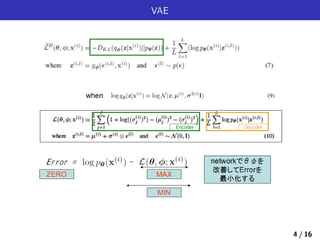
log pθ(x(1)
, · · · , x(N)
) =
N∑
i=1
log pθ(x(i)
) (5)
log pθ(x(i)
) = DKL(qϕ(z|x(i)
)||pθ(z|x(i)
)) + L(θ, ϕ : x(i)
) (6)
log pθ(x(i)
) ≥ L(θ, ϕ : x(i)
) (7)
L(θ, ϕ : x(i)
) = Eqϕ(z|x)[− log qϕ(z|x) + log pθ(x, z)] (8)
= −DKL(qϕ(z|x(i)
)||pθ(z)) + Eqϕ(z|x(i))[log pθ(x(i)
|z)] (9)
3 / 16

4. VAE
4 / 16

5. VAE
5 / 16

6. VAE Programming
6 / 16

7. VAE Programming
7 / 16

8. Lower Band
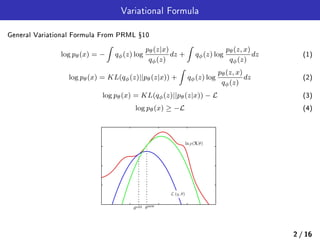
General Lower Band Formula from PRML Ÿ10
−L =
∫
qϕ(z) log
pθ(z, x)
qϕ(z)
dz (10)
−L = Eqϕ(z)[log pθ(z, x) − log qϕ(z)] (11)
−L =
∫
qϕ(z) log
pθ(x|z)pθ(z)
qϕ(z)
dz (12)
−L =
∫
qϕ(z)
(
log pθ(x|z) + log
pθ(z)
qϕ(z)
)
dz (13)
−L = Eqϕ(z)[log pθ(x|z)] − KL(pθ(z)||qϕ(z)) (14)
8 / 16

9. Semi-supervised Model
x:Unsupervised value
y:Semi-supervised value
z:Latent value
Figure: Encoder and Decorder Graphical Model
9 / 16

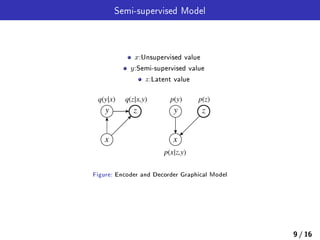
10. Lower Bands of Semi-supervised Model
Lower Band for Semi-supervised for z by x and y (labeled Band)
−L(x, y) = Eqϕ(z|x,y)[log pθ(x|y, z)] − KL(pθ(z)pθ(y)||qϕ(z|x, y)) (15)
= Eqϕ(z|x,y)[log pθ(x|y, z) + log pθ(z) + log pθ(y) − log qϕ(z|x, y)] (16)
Lower Band for Semi-supervised for y and z by x (unlabeled Band)
−U(x) = Eqϕ(z,y|x)[log pθ(x|y, z)] − KL(pθ(z)pθ(y)||qϕ(z, y|x)) (17)
= Eqϕ(z,y|x)[log pθ(x|y, z) + log pθ(z) + log pθ(y) − log qϕ(z, y|x)] (18)
10 / 16

11. Detail : Semi-supervised for y and z by x (Unlabeled Band)
We use qϕ(z, y|x) = qϕ(z|y, x)qϕ(y|x)
−U(x) = Eqϕ(z|y,x)qϕ(y|x)
[log pθ(x|y, z) + log pθ(z) + log pθ(y) − log(qϕ(z|y, x)qϕ(y|x))](19)
=
∑
y
qϕ(y|x)(Eqϕ(z|y,x)
[log pθ(x|y, z) + log pθ(z) + log pθ(y) − log qϕ(z|y, x)
− log qϕ(y|x)]) (20)
=
∑
y
qϕ(y|x)
(
L(x, y) − Eqϕ(z|y,x)[log qϕ(y|x)]
)
(21)
=
∑
y
qϕ(y|x)
(
L(x, y) − log qϕ(y|x)
)
(22)
=
∑
y
qϕ(y|x) (L(x, y)) − H[qϕ(y|x)] (23)
Here we use
∑
y
qϕ(y|x)[log pϕ(y|x)] = H[qϕ(y|x)] (24)
11 / 16

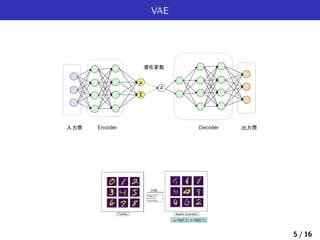
12. Loss Function and VAE Structure
J =
∑
(x,y)∼plabel
L(x, y) +
∑
x∼punlabel
U(x) (25)
Add Classification LossforM2Model
=
∑
(x,y)∼plabel
L(x, y) +
∑
x∼punlabel
U(x) + α · Ep(x,y)[− log qϕ(y|x)] (26)
12 / 16

13. Supervised VAE Structure M1 model
−L(x, y) = Eqϕ(z|x,y)[log pθ(x|y, z) + log pθ(z) + log pθ(y) − log qϕ(z|x, y)]
Figure: Supervised Model
13 / 16

14. Semi-Supervised VAE Structure M1 model
−U(x) =
∑
y
qϕ(y|x) (L(x, y)) − H[qϕ(y|x)]
J =
∑
(x,y)∼plabel
L(x, y) +
∑
x∼punlabel
U(x)
Figure: xLyL:Labeled xU Unlabeled
14 / 16

15. Semi-Supervised VAE Result
Figure: 50000 records N:Labeled Error rate
15 / 16

16. Semi-Supervised VAE Result
Figure: lower: Fixed type and any class
16 / 16