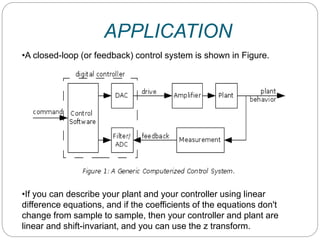
The document discusses the z-transform as a tool for analyzing closed-loop control systems, emphasizing its applications in linear and shift-invariant systems. It explains how the z-transform converts difference equations into algebraic equations, facilitating easier problem-solving and system behavior prediction. Additionally, it highlights the efficiency of using software to convert transfer functions into z-domain equations and subsequently into difference equations, streamlining the control system design process.

2. APPLICATION
•A closed-loop (or feedback) control system is shown in Figure.
•If you can describe your plant and your controller using linear
difference equations, and if the coefficients of the equations don't
change from sample to sample, then your controller and plant are
linear and shift-invariant, and you can use the z transform.

3. HOW?
 Suppose xn=output of the plant at sample time n
un=command to the DAC at sample time n
a and b=constants set by the design of the plant
 You can solve the behaviour equation of the plant over
time.
 Furthermore you can also investigate what happens when
you add feedback to the system.
 The z transform allows you to do both of these things.

4. THERE’S MORE…
 Deals with many common feedback control
problems using continuous-time control.
 Also used in sampled-time control situations to
deal with linear shift-invariant difference
equations.

5. Z-Transform at WORK
 Z-Transform takes a sequence of xn numbers
and transforms it into an expression X(Z) that
depends on the variable Z but not n. That's the
transform part.
 So the problem is transformed from the sampled
time domain (n) to the z domain.

6. Z-Transform Formation
 The z transform of x is denoted as Z(x) and
defined as,

7. EXAMPLE
 Figure shows a motor and gear train that we
might use in a servo system.
 Here the difference equation that describes the
plant might look like

8.  We can take the z transform of the
behaviour equation without knowing
what xn or un are and get,
 Notice a cool thing: We've turned the
difference equation into an algebraic
equation!
 This one of the many things that makes
the z transform so useful because we
can now easily solve the algebraic

9. Transfer Function
 The function H(Z) is called the “Transfer
Function" of the system – it shows how the input
signal is transformed into the output signal.
H(Z)=Y(Z)/X(Z)
 In Z domain, the Transfer Function of a system
isn't affected by the nature of the input signal, nor
does it vary with time.

10.  We can predict the behavior of the motor
using H(Z).
 Let's say we want to see what the motor will
do if x goes from 0 to 1 at time n = 0, and
stays there forever. This is called the ‘unit step
function’ and the Z-Transform of the unit step
response is H(Z)=Z/(Z-1).
 Thus we can know everything about the
system behaviour and avoid undesirable
situations.

11. SOFTWARE
 You can write software from the Z-Transform with
utter ease.
 Like, if you have a Transfer Function of a system,
then the software turns it into a Z-domain
equation which can then be converted into a
difference equation which in turn can be turned
into a software very quickly.
 This saves the manual work and a software for a
plant can be produced within seconds.

12. THANK YOU