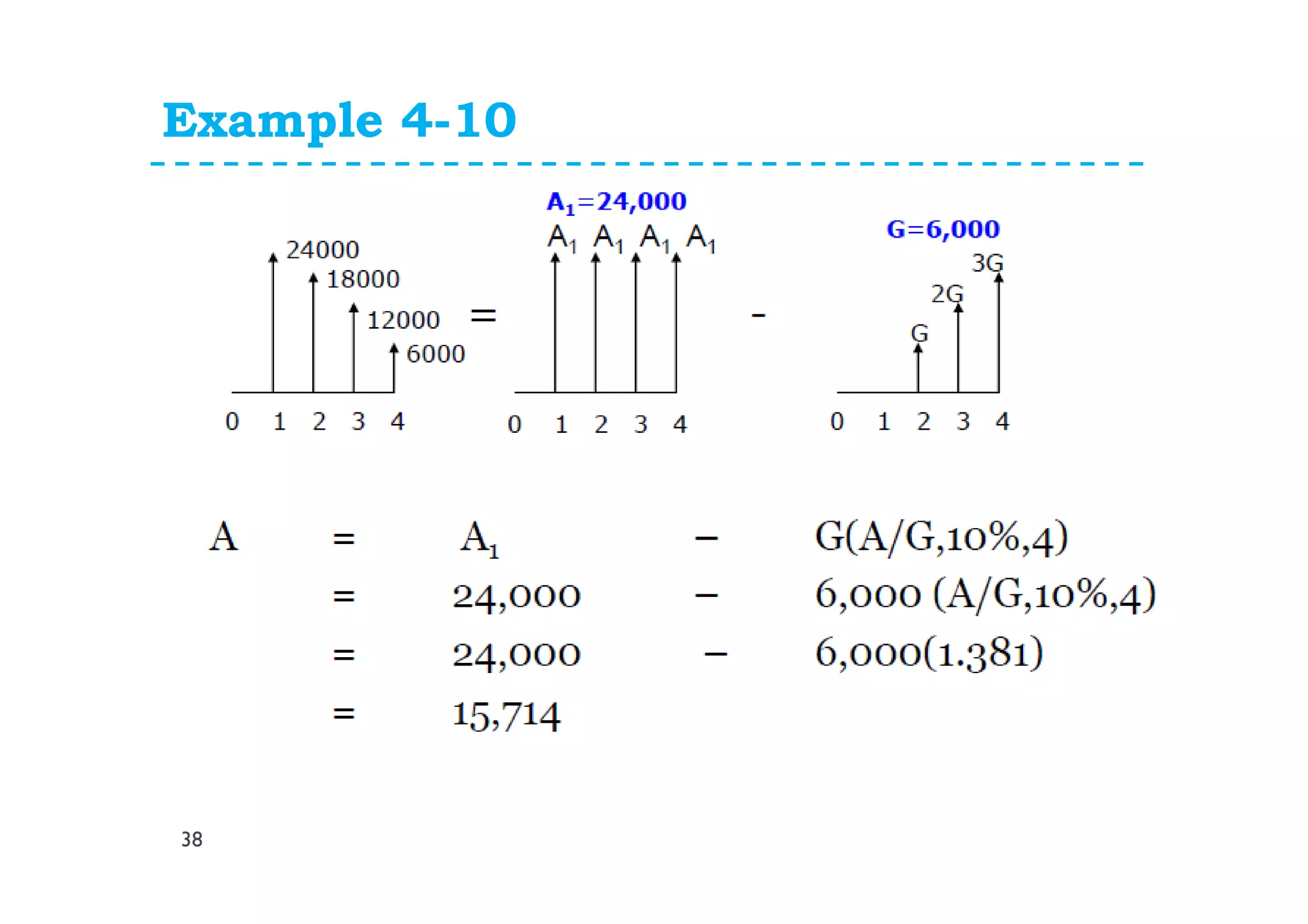
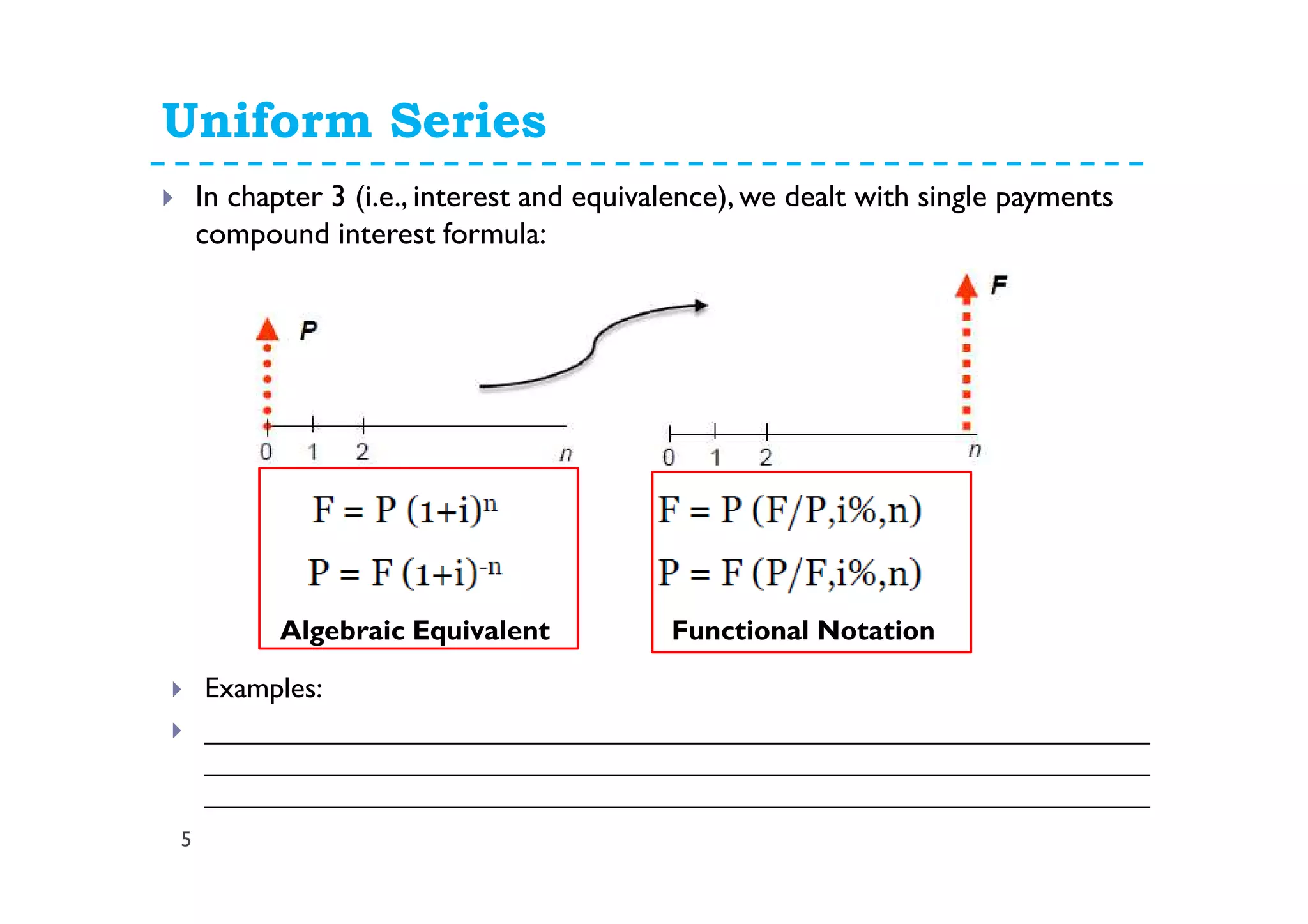
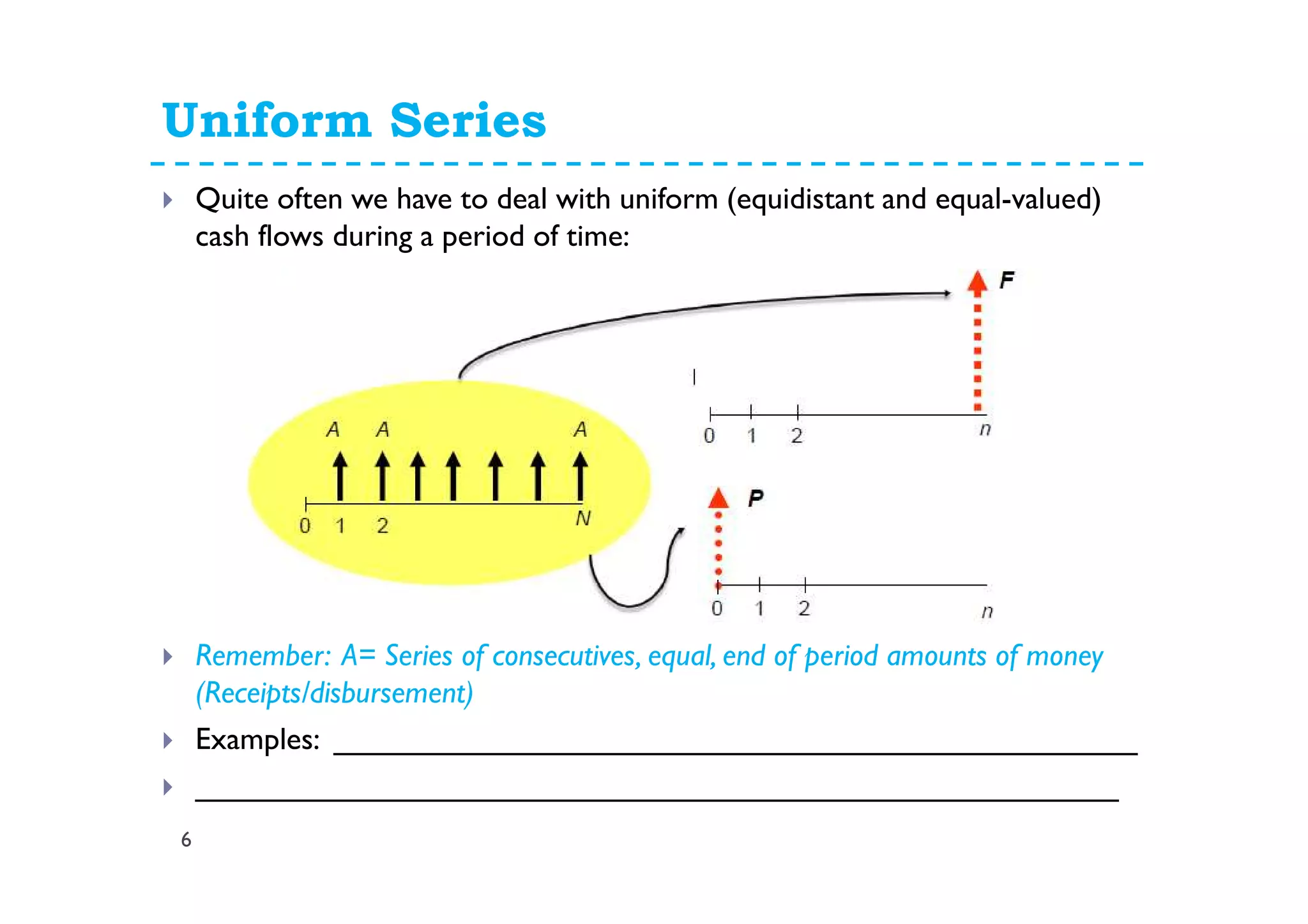
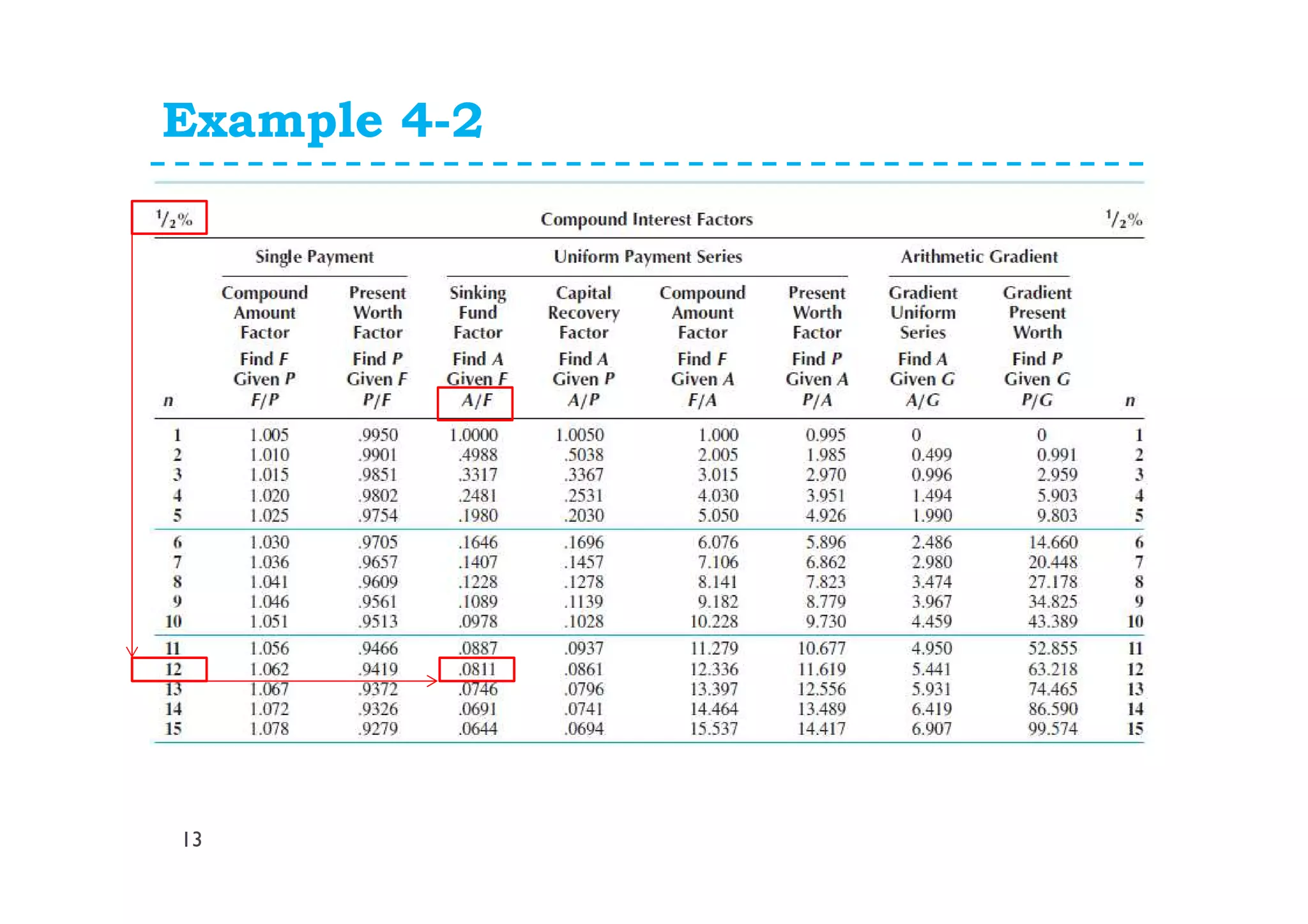
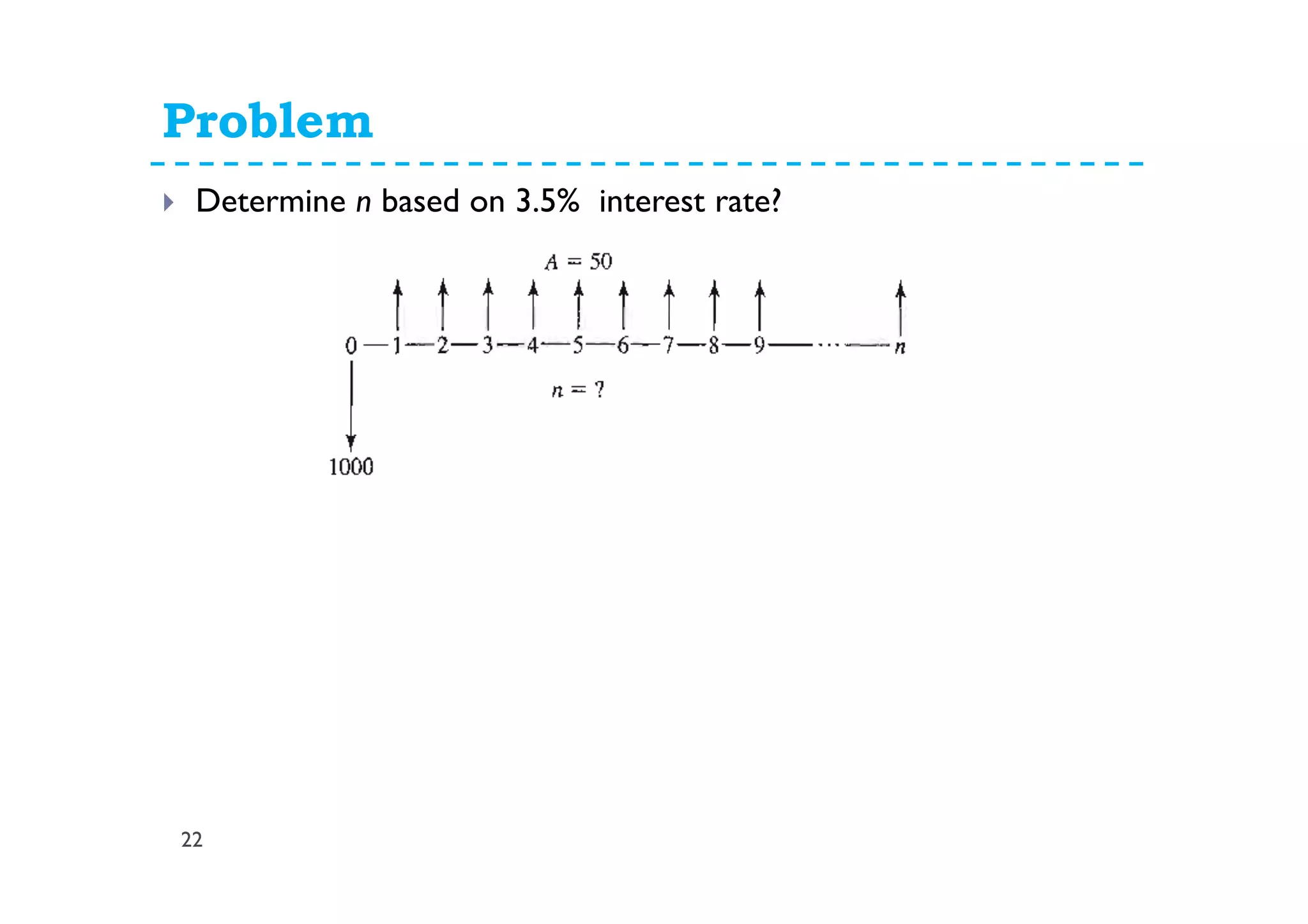
This document provides lecture notes on uniform series and arithmetic gradient interest formulas. It begins by deriving the uniform series compound interest formula and defines the uniform series compound amount factor. It then derives the uniform sinking fund formula and defines the uniform series sinking fund factor. Similar derivations are shown for the uniform capital recovery factor and present worth factor. The document then discusses arithmetic gradient series where cash flows increase by a fixed amount each period. It derives the arithmetic gradient future worth factor and present worth factor. Examples are provided to demonstrate applying these formulas.

1. 5. More Interest Formulas
Dr. Mohsin Siddique
Assistant Professor
msiddique@sharjah.ac.ae
Ext: 29431
Date: 21/10/2014
Engineering Economics
University of Sharjah
Dept. of Civil and Env. Engg.

2. 2
Part I

3. Outcome of Today’s Lecture
3
After completing this lecture…
The students should be able to:
Understand uniform series compound interest formulas

4. More interest Formulas
4
Uniform Series
Arithmetic Gradient
Geometric Gradient
Nominal and Effective Interest
Continuous Compounding

5. Uniform Series
5
In chapter 3 (i.e., interest and equivalence), we dealt with single payments
compound interest formula:
Functional NotationAlgebraic Equivalent
Examples:
__________________________________________________________
__________________________________________________________
__________________________________________________________

6. Uniform Series
6
Quite often we have to deal with uniform (equidistant and equal-valued)
cash flows during a period of time:
Remember: A= Series of consecutives, equal, end of period amounts of money
(Receipts/disbursement)
Examples: _______________________________________________
______________________________________________________

7. Deriving Uniform Series Formula
7
Let’s compute Future Worth, F, of a stream of equal, end-of-period
cash flows, A, at interest rate, i, over interest period, n
0 1 2 3 4
F
0 1 2 3 4
A
F1
0 1 2 3 4
A
F2
0 1 2 3 4
A
F4
0 1 2 3 4
A
F3
0 1 2 n-1 n
A
F
= +
++
F=F1+F2+F3+F4
Recall
( )3
1F1 iA += ( )2
1F2 iA +=
( )1
1F3 iA += ( )0
1F4 iA +=
Let n=4

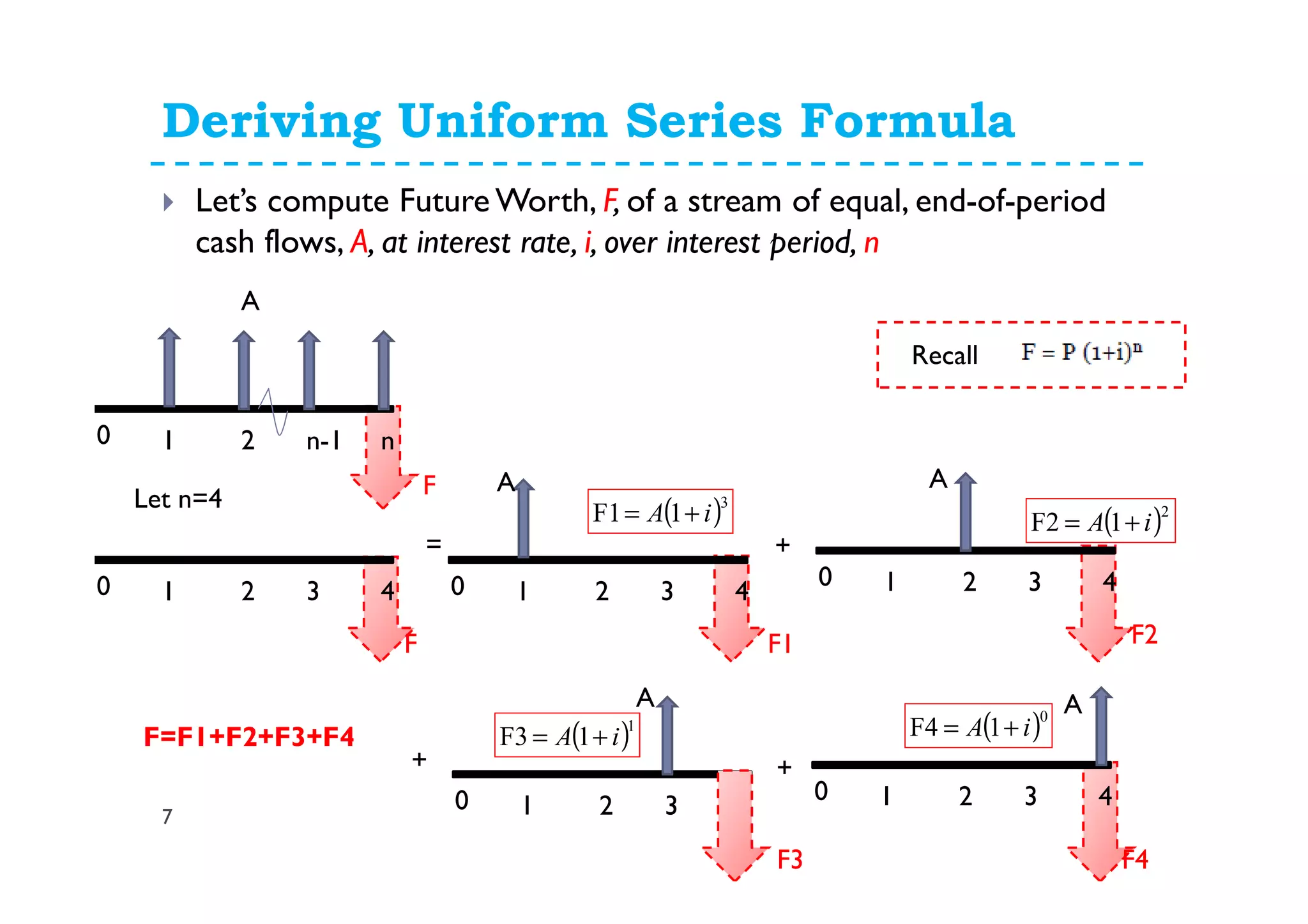
8. Deriving Uniform Series Formula
0 1 2 3 4
A F
F=F1+F2+F3+F4
( )3
1F1 iA += ( )2
1F2 iA +=
( )1
1F3 iA += ( )0
1F4 iA +=
F =
+ +
+
( ) ( ) ( ) AiAiAiA ++++++=
123
111F
For general case, we can write that
Multiplying both sides with (1+i)
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )[ ]iiiiAi
iAiAiAiAi
nnn
nnn
++++++++=+
++++++++=+
−−
−−
1...1111F
1...1111F
21
21
( ) ( ) ( )
( ) ( ) ( )[ ]1...111
...111
321
321
+++++++=
+++++++=
−−−
−−−
nnn
nnn
iiiAF
AiAiAiAF
Eq. (1)
Eq. (2)

9. Deriving Uniform Series Formula
9
Eq. (2)-Eq. (1)
( ) ( ) ( ) ( ) ( )[ ]iiiiAi
nnn
++++++++=+
−−
1...1111F
21
( ) ( ) ( )[ ]1...111
321
+++++++=
−−− nnn
iiiAF
Eq. (2)
Eq. (1)
-
( )[ ]11iF −+=
n
iA
( ) [ ]niAFA
i
i
A
n
%,,/
11
F =




 −+
=
Eq. (3)
Eq. (4)
( )





 −+
i
i
n
11
Where is called uniform series compound
amount factor and has notation [ ]niAF %,,/

10. Deriving Uniform Series Formula
10
Eq. (4) can also be written as
( )
[ ]niFAF
i
i
F n
%,,/
11
A =





−+
=
( ) 





−+ 11
n
i
i
Where is called uniform series sinking fund
factor and has notation [ ]niFA %,,/
Eq. (5)






ni
given
Find
%,,

11. Example 4-1
11

12. Example 4-2
12
( )
=





−+
=
11
A n
i
i
F

13. Example 4-2
13

14. Deriving Uniform Series Formula
14
If we use the sinking fund formula (Eq. 5) and substitute the single payment
compound amount formula, we obtain
( )
( )
( ) 





−+
+=





−+
=
11
1
11
A n
n
n
i
i
iP
i
i
F ( )n
iPF += 1Q
( )
( )
( )niPAP
i
ii
P n
n
%,,/
11
1
A =





−+
+
=
It means we can determine the values of A when the present sum P
is known
Where is called uniform series capital
recovery factor and has notation
( )
( ) 





−+
+
11
1
n
n
i
ii
( )niPAP %,,/
Eq. (6)

15. Deriving Uniform Series Formula
15
Eq. (6) can be rewritten as
( )
( )
( )niAPA
ii
i
A n
n
%,,/
1
11
P =





+
−+
=
It means we can determine present sum P when the value of A is
known
Where is called uniform series present
worth factor and has notation
( )
( ) 





+
−+
n
n
ii
i
1
11
( )niAPA %,,/
Eq. (7)

16. Example 4-3
16

17. Example 4-6
17

18. Example 4-6
18

19. Example 4-6
19

20. Example 4-7
20
0 1 2 3 4

21. 21

22. Problem
22
Determine n based on 3.5% interest rate?
Solution:
P = A (P/A, 3.5%, n)
$1,000 = $50 (P/A, 3.5%, n)
(P/A, 3.5%, n) = 20
From the 3.5% interest table, n = 35.

23. Problem
23
A sum of money is invested at 2% per 6 month period (semi-annually) will
double in amount in approximately how much years?
P = $1 n = unknown number of
semiannual periods
i = 2% F = 2
F = P (1 + i)n
2 = 1 (1.02)n
2 = 1.02n
n = log (2) / log (1.02)
= 35
Therefore, the money will double in 17.5 years.

24. 24
Part II
(from next class bring interest tables and formula sheet)

25. Outcome of Today’s Lecture
25
After completing this lecture…
The students should be able to:
Understand arithmetic gradient interest formulas

26. More interest Formulas
26
Uniform Series
Arithmetic Gradient
Geometric Gradient
Nominal and Effective Interest
Continuous Compounding

27. Arithmetic Gradient Series
27
It’s frequently happen that the cash
flow series is not constant amount.
It probably is because of operating
costs, construction costs, and
revenues to increase of decrease
from period to period by a
constant percentage

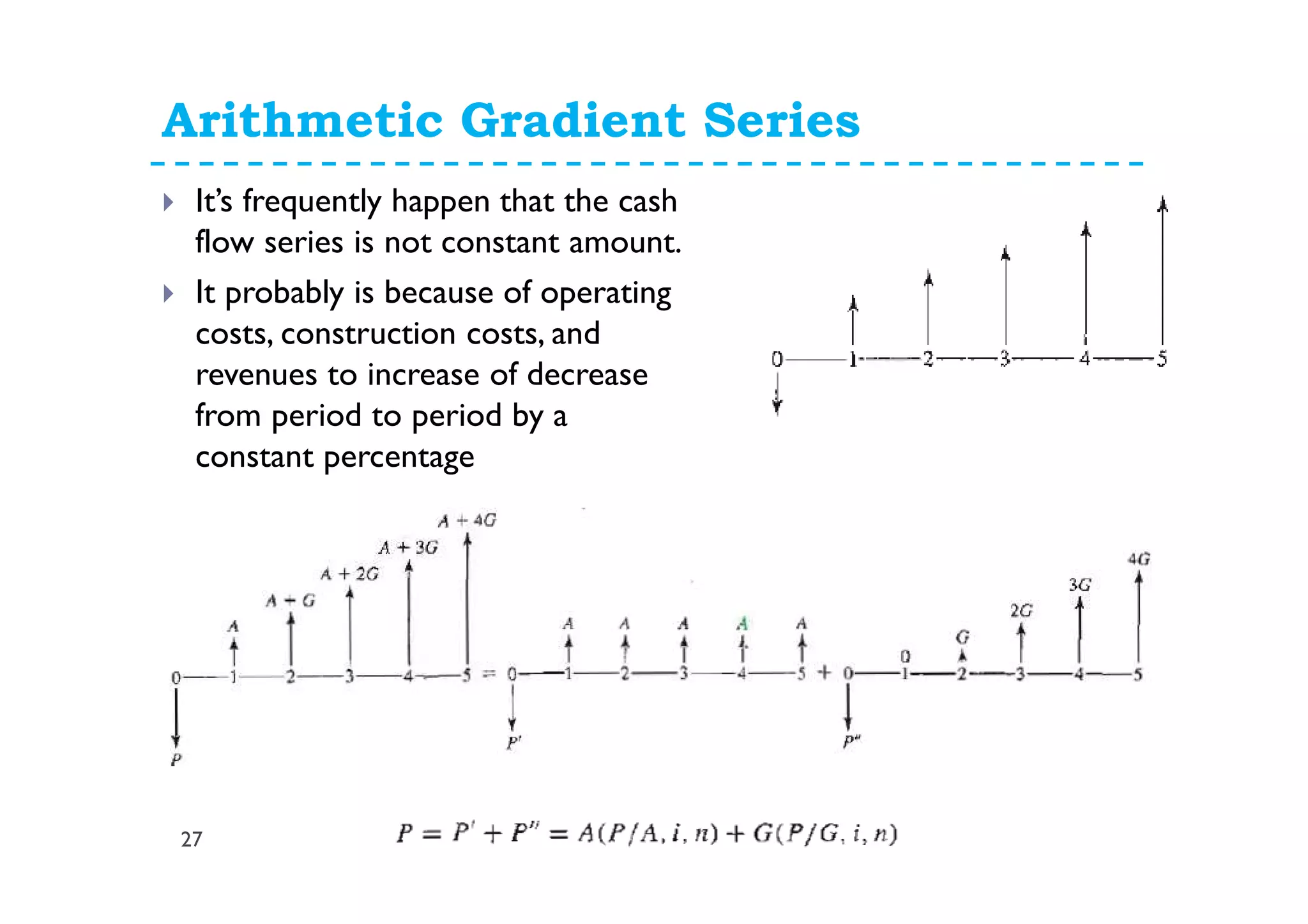
28. Arithmetic Gradient Series
28
Let the cash flows increase/decrease by a uniform fixed amount G
every subsequent period
Eq. (1)
Recall
( ) ( ) ( )
( ) ( ) ( )[ ])1(1)2(...121F
)1()1(1)2(...121F
132
0132
−++−+++++=
+−++−+++++=
−−
−−
niniiG
iGniGniGiG
nn
nn

29. Arithmetic Gradient Series
29
Multiplying Eq. (1) with (1+i), we get
( ) ( ) ( ) ( )[ ]1221
)1)(1(1)2(...121Fi1 ininiiG
nn
+−++−+++++=+
−−
( ) ( ) ( ) ( )[ ]1221
)1)(1(1)2(...121Fi1 ininiiG
nn
+−++−+++++=+
−−
( ) ( ) ( )[ ])1(1)2(...121F
132
−++−+++++=
−−
niniiG
nn
( ) ( ) ( ) ( )[ ]
( ) ( ) ( ) ( )[ ] nGiiiiG
niiiiG
nn
nn
−+++++++++=
+−++++++++=
−−
−−
111...11iF
111...11iF
1221
1221
Eq. (2)-Eq. (1)
Eq. (2)
-
( )
( ) ( )





 −−+
=





−
−+
=
−




 −+
=
2
1111
11
iF
i
nii
Gn
i
i
i
G
F
nG
i
i
G
nn
n
( ) [ ]niGFG
i
ini
GF
n
%,,/
11
2
=




 −−+
=
Eq. (3)
Eq. (4)
Arithmetic
gradient future
worth factor

30. 30
( ) ( ) ( ) ( ) ( ) ( )[ ] ( )
( ) ( ) ( ) ( )[ ]
( )[ ]
( ) nG
i
i
GiF
nGiiGiiF
nGiiiiG
inGiiiiiGi
n
n
nn
nn
−




 −+
=
−−+=
−+++++++++=
+−++++++++++=+
−−
−
11
11
111...11iF
1111...111iF
1221
231
-

31. Arithmetic Gradient Series
31
Substituting F from single payment compound formula, we can write
Eq.(4) as
( )
( )
[ ]niGPG
ii
ini
GP n
n
%,,/
1
11
2
=





+
−−+
=
Eq. (5)
(P/G ,i%, n) is known as Arithmetic gradient present worth factor
Now substituting value of F from uniform series compound amount
factor, we can write Eq. (4) as
Recall
( ) ( )
( )( )
( )( )
( )niGAGA
ii
inii
GA
i
i
A
i
ini
GF
n
n
nn
%,,/
11
11
1111
2
2
=






−+
−−+
=





 −+
=




 −−+
=
( )





 −+
=
i
i
A
n
11
FQ
(A/G, i%, n) is known as Arithmetic gradient uniform series factor

32. Arithmetic Gradient Series
32

33. Example 4-8
33
Suppose you buy a car.You wish to set up enough money in a bank
account to pay for standard maintenance on the car for the first five
years.You estimate the maintenance cost increases by G = $30 each
year.The maintenance cost for year 1 is estimated as $120. i = 5%.
Thus, estimated costs by year are $120, $150, $180, $210,
$240.
=

34. Example 4-8
34

35. Example 4-9
35
Maintenance costs of a machine start at $100 and go up by $100
each year for 4 years.What is the equivalent uniform annual
maintenance cost for the machinery if i= 6%.
=
A=?

36. Example 4-9
36

37. Example 4-10
37

38. Example 4-10
38

39. Example
39
(Hint: look for differences in time axis.)

40. 40
ThankYou
Feel Free to Contact
msiddique@sharjah.ac.ae
Tel. +971 6 5050943 (Ext. 2943)