The document provides information on capital investment problems and cash flows, focusing on factors related to how time and interest affect money. It discusses single payment factors to find the future or present value of a single amount. It also covers uniform series factors to relate the present worth, future worth, or annual equivalent of a uniform series of cash flows. Finally, it examines gradient formulas, including arithmetic gradients where cash flows change by a constant amount each period, and geometric gradients where they change by a constant percentage each period. Formulas and examples are provided for each type of cash flow problem.

1. EGN 3203 Engineering Economics
LO 2 – b
Capital Investment Problems &
Cash Flow

2. Factors: How Time and Interest Affect
Money.
PURPOSE
Account for the time value
of money using
tabulated factors,
spreadsheet functions,
and calculator functions
TOPICS
 Single amount factors –
F/P, P/F
 Uniform series factors –
P/A, A/P, F/A, A/F
 Gradients – arithmetic and
geometric
 Spreadsheet/calculator use

3. Fundamental equation determines amount F accumulated after
t = 1, 2, …, n years for a single present amount P
F1 = P + Pi = P(1 + i)
F2 = F1 + F1i
= P(1 + i) + P(1 + i)i
= P(1 + i)2
Ft = P(1 + i)t
Fn = P(1 + i)n
Factors: How Time and Interest Affect
Money: Single Payment Factors

4. Factors: How Time and Interest Affect
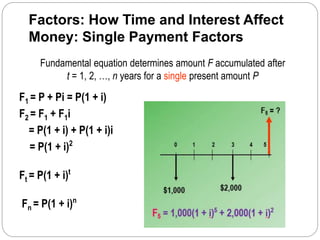
Money: Single Payment Factors
Find F, given P
Formula: F = P(1 + i)n
Notation: F=P(F/P,i%,n)
(1+i)n
= single-payment compound
amount factor
Spreadsheet: = FV(i%,n,,P)
Calculator: FV(i,n,A,P)
Find P, given F
Formula: P = F[1/(1 + i)n
]
Notation: P=F(P/F,i%,n)
1/(1+i)n
= single-payment present
worth factor
Spreadsheet: = PV(i%,n,,F)
Calculator: PV(i,n,A,F)

5. Find F, given P
Formula: F = P(1 + i)n
Notation: F=P(F/P,i%,n)
(1+i)n
= single-payment compound
amount factor
Spreadsheet: = FV(i%,n,,P)
Calculator: FV(i,n,A,P)
Find P, given F
Formula: P = F[1/(1 + i)n
]
Notation: P=F(P/F,i%,n)
1/(1+i)n
= single-payment present
worth factor
Spreadsheet: = PV(i%,n,,F)
Calculator: PV(i,n,A,F)
Factors: How Time and Interest Affect
Money: Single Payment Factors

6. Example: Ada, Inc. can pay $10,000 now or $15,000 five years from now for power back-
up equipment. Are P and F values equivalent at 5% per year?
Factors: How Time and Interest Affect
Money: Single Payment Factors

7. Example: Ada, Inc. can pay $10,000 now or $15,000 five years from now for power back-
up equipment. Are P and F values equivalent at 5% per year?
Factors: How Time and Interest Affect
Money: Single Payment Factors

8. Single Payment Factors F/P :Example
Sol.

9. Single Payment Factors P/F : Example
Sol.

10.  Notes

11. UNIFORM SERIES FORMULAS
(A/F, F/A) (P/A, A/P )
There are four uniform series formulas that involve A, where A
means that:
 The cash flow occurs in consecutive interest periods, and
 The cash flow amount is the same in each period.
The formulas relate a
present worth P or a future
worth F to a uniform
series amount A. The two
equations that relate P and
A are as follows.
The uniform series
formulas that relate A and
F are as follow.

12. Uniform Series Involving
P/A and A/P
0 1 2 3 4 5
A = ?
P = Given
The cash flow diagrams are:
Standard Factor NotationP = A(P/A,i,n) A = P(A/P,i,n)
Note: P is one period Ahead of first A value
(1) Cash flow occurs in consecutive interest periods
The uniform series factors that involve P and A are derived as follows:
(2) Cash flow amount is same in each interest period
0 1 2 3 4 5
A = Given
P = ?

13. Example: Uniform Series Involving P/A
A chemical engineer believes that by modifying the structure of a certain water
treatment polymer, his company would earn an extra $5000 per year. At an interest
rate of 10% per year, how much could the company afford to spend now to just
break even over a 5 year project period?
(A) $11,170 (B) 13,640 (C) $15,300 (D) $18,950
The cash flow diagram is as follows:
P = 5000(P/A,10%,5)
= 5000(3.7908)
= $18,954
Answer is (D)
0 1 2 3 4 5
A = $5000
P = ? i =10%
Solution:

14. Uniform Series Involving F/A and A/F
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
2-14
(1) Cash flow occurs in consecutive interest periods
The uniform series factors that involve F and A are derived as follows:
(2) Last cash flow occurs in same period as F
0 1 2 3 4 5
F = ?
A = Given
0 1 2 3 4 5
F = Given
A = ?
Note: F takes place in the same period as last A
Cash flow diagrams are:
Standard Factor NotationF = A(F/A,i,n) A = F(A/F,i,n)

15. Example: Uniform Series Involving
F/A
An industrial engineer made a modification to a chip manufacturing
process that will save her company $10,000 per year. At an interest rate
of 8% per year, how much will the savings amount to in 7 years?
(A) $45,300 (B) $68,500 (C) $89,228 (D) $151,500
The cash flow diagram is:
A = $10,000
F = ?
i = 8%
0 1 2 3 4 5 6 7
Solution:
F = 10,000(F/A,8%,7)
= 10,000(8.9228)
= $89,228
Answer is (C)

16. Uniform Series Involving
P/A and A/P

17. Uniform Series Involving F/A and A/F

18. Uniform Series Involving F/A and A/F

19. GRADIENT FORMULAS
 The previous four equations involved cash flows
of the same magnitude A in each interest period.
 Sometimes the cash flows that occur in
consecutive interest periods are not the same
amount (not an A value), but they do change in a
predictable way.
 These cash flows are known as gradients, and
there are two general types: arithmetic and
geometric.

20. © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
2-20
Arithmetic Gradients
Arithmetic gradients change by the same amount each period
The cash flow diagram for the PG
of an arithmetic gradient is:
0
1 2 3 n
G
2G
4
3G
(n-1)G
PG = ?
G starts between periods 1 and
2
(not between 0 and 1)
This is because cash flow in year 1 is
usually not equal to G and is handled
separately as a base amount
(shown on next slide)
Note that PG is located Two
Periods Ahead of the first
change that is equal to G
Standard factor notation is
PG = G(P/G,i,n)

21. © 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
2-21
Typical Arithmetic Gradient Cash Flow
PT = ?
i = 10%
0 1 2 3 4 5
400
450
500
550
600
PA = ?
i = 10%
0 1 2 3 4 5
400 400 400 400 400
PG = ?
i = 10%
0 1 2 3 4 5
50
100
150
200
+
This diagram = this base amount plus this gradient
PA = 400(P/A,10%,5) PG = 50(P/G,10%,5)
PT = PA + PG = 400(P/A,10%,5) + 50(P/G,10%,5)
Amount
in year 1
is base
amount
Amount in year 1
is base amount

22. Converting Arithmetic Gradient to A
© 2012 by McGraw-Hill, New York, N.Y All Rights Reserved
2-22
i = 10%
0 1 2 3 4 5
G
2G
3G
4G
i = 10%
0 1 2 3 4 5
A = ?
Arithmetic gradient can be converted into equivalent A value using G(A/G,i,n)
General equation when base amount is involved is
A = base amount + G(A/G,i,n)
0 1 2 3 4 5
G
2G
3G
4G
For decreasing gradients,
change plus sign to minus
A = base amount - G(A/G,i,n)

23. Example: Arithmetic Gradient
The present worth of $400 in year 1 and amounts increasing by
$30 per year through year 5 at an interest rate of 12% per year is
closest to:
(A) $1532 (B) $1,634 (C) $1,744 (D) $1,829
0 1 2 3 Year
430
460
4
490
520
PT = ?
5
400
i = 12%
G = $30
= 400(3.6048) + 30(6.3970)
= $1,633.83
Answer is (B)
PT = 400(P/A,12%,5) + 30(P/G,12%,5)
The cash flow could also be converted
into an A value as follows:
A = 400 + 30(A/G,12%,5)
= 400 + 30(1.7746)
= $453.24
Solution:

24.  P/G factor formula for gradient only
 A/G factor for annual equivalent, gradient only
 P/G and A/G factors are tabulated. There are no
direct spreadsheet or calculator functions
Gradient Formulas:
Arithmetic Gradients

25.  Example: Estimated annual revenue of $5,000
increases by $500 per year starting next year. Find
P and A over an 8-year period at i = 10%.
Arithmetic Gradients

26.  Solution:
P = A(P/A,i%,n) + G(P/G,i%.n)
= 5000(P/A,10%,8) + 500(P/G,10%,8) = $34,689
A = 5000 + 500(A/G,10%,8)
= 5000 + 500(A/G,10%,8) = $6,502 per year
Arithmetic Gradients

27. Arithmetic Gradients

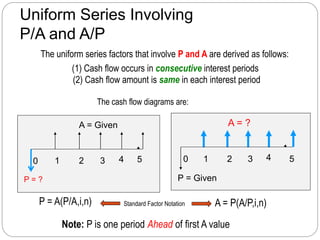
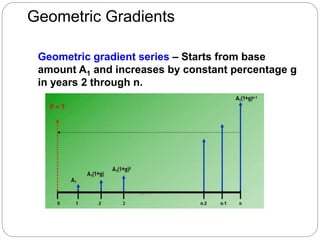
28. Geometric Gradients
Geometric gradients change by the same percentage each period
0
1 2 3 n
A1
A 1(1+g)1
4
A 1(1+g)2
A 1(1+g)n-1
Pg = ?
There are no tables for geometric factors
Use following equation for g ≠ i:
Pg = A1{1- [(1+g)/(1+i)]n}/(i-g)
where: A1 = cash flow in period 1
g = rate of increase
If g = i, Pg = A1n/(1+i)
Note: If g is negative, change signs in front of both g values
Cash flow diagram for present worth
of geometric gradient
Note: g starts between
periods 1 and 2

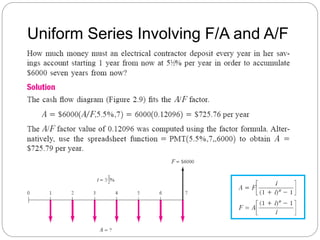
29. Example: Geometric Gradient
Find the present worth of $1,000 in year 1 and amounts
increasing by 7% per year through year 10. Use an
interest rate of 12% per year.
(a) $5,670 (b) $7,333 (c) $12,670 (d) $13,550
0
1 2 3 10
1000
1070
4
1145
1838
Pg = ? Solution:
Pg = 1000[1-(1+0.07/1+0.12)10]/(0.12-0.07)
= $7,333
Answer is (b)
g = 7%
i = 12%
To find A, multiply Pg by (A/P,12%,10)

30. Geometric gradient series – Starts from base
amount A1 and increases by constant percentage g
in years 2 through n.
Geometric Gradients

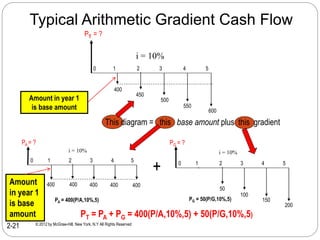
31. Geometric gradient series
Gradient Formulas:
 Present worth – No
tabulated factors
 This is P for all cash
flows, including A1
 Term in brackets is
(P/A,g,i%,n) factor
 When g = i, relation
reduces to
P = A1[n/(1+i)]
Example: Payroll totals
$250,000 this year;
expected to grow at 5%
per year through year 5.
Find P at i = 12%.
Year 1: $250,000
Year 5: 250,000(1.05)4
= 303,876
= 250,000(3.94005)
= $985,013
Geometric Gradients

32. Geometric Gradients : Example

33. Notes