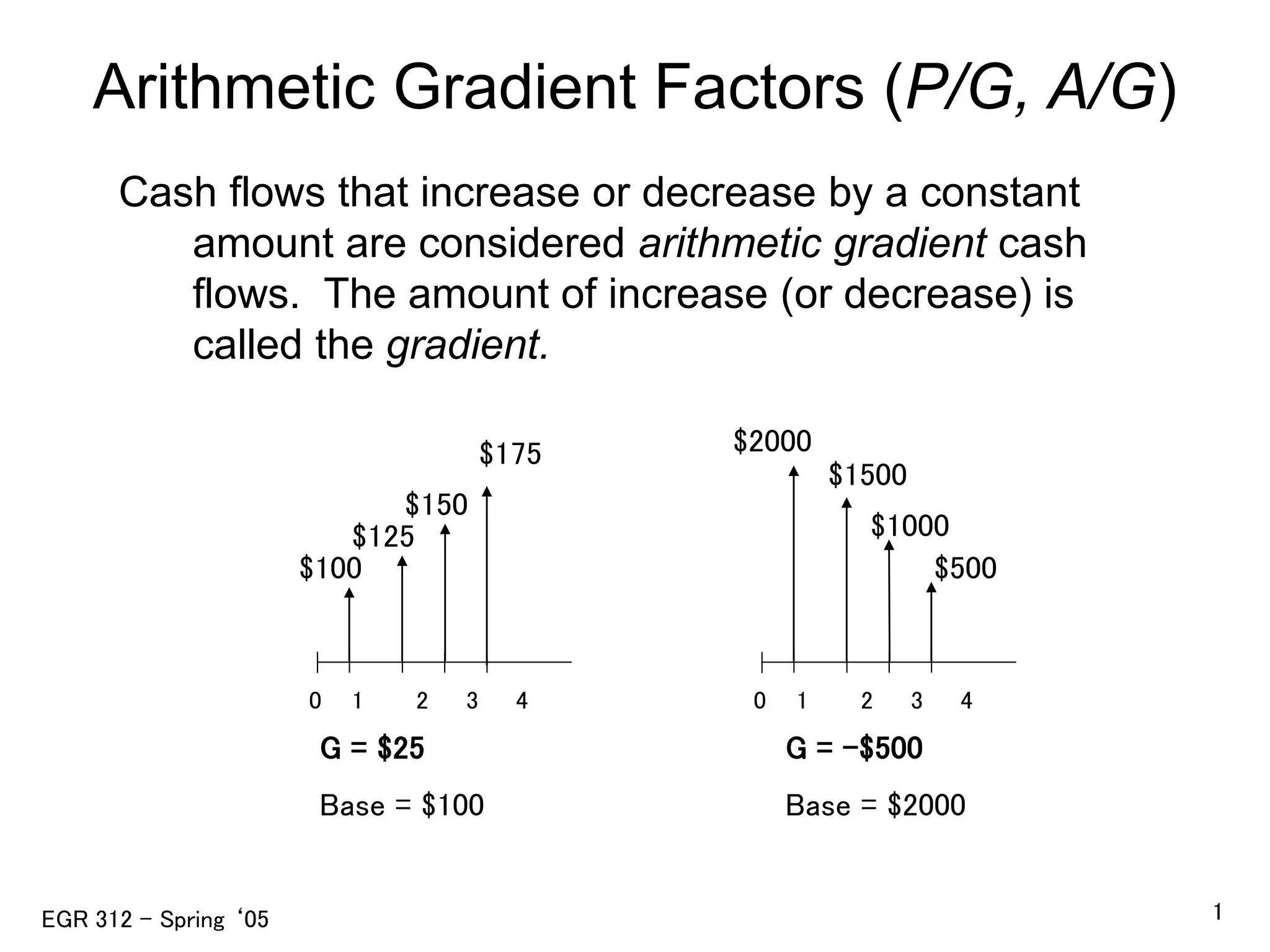
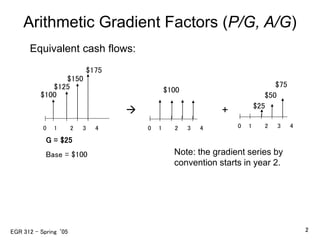
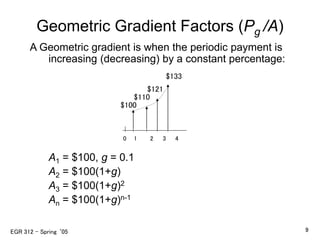
This document discusses arithmetic and geometric gradient cash flows. It defines arithmetic gradient cash flows as those that increase or decrease by a constant amount each period, called the gradient. It provides formulas to calculate the present value (P) of arithmetic gradient cash flows using the gradient (G) and arithmetic gradient factors. It also discusses determining unknown interest rates and number of periods from single-payment and uniform-series cash flows using formulas, tables, and Excel functions.

1. EGR 312 – Spring ‘05 1
Arithmetic Gradient Factors (P/G, A/G)
Cash flows that increase or decrease by a constant
amount are considered arithmetic gradient cash
flows. The amount of increase (or decrease) is
called the gradient.
$100
$125
$150
$175
G = $25
Base = $100
0 1 2 3 4
$2000
$1500
$1000
$500
G = -$500
Base = $2000
0 1 2 3 4

2. EGR 312 – Spring ‘05 2
Arithmetic Gradient Factors (P/G, A/G)
Equivalent cash flows:
 +
Note: the gradient series by
convention starts in year 2.
$100
$125
$150
$175
G = $25
Base = $100
0 1 2 3 4 0 1 2 3 4
$100
0 1 2 3 4
$25
$50
$75

3. EGR 312 – Spring ‘05 3
Arithmetic Gradient Factors (P/G, A/G)
To find P for a gradient cash flow that starts at the end
of year 2 and end at year n:
or P = G(P/G,i,n)
where (P/G,i,n) =
0 1 2 3 …
n
G
2G
nG
P











 n
n
n
i
n
i
i
i
i
G
P
)
1
(
)
1
(
1
)
1
(











n
n
n
i
n
i
i
i
i )
1
(
)
1
(
1
)
1
(
1

4. Problems
1. The maintenance on a machine is
expected to be $155 at the end of the
first year, and increasing $35 each year
for the following seven years. What
present of money would need to be set
aside now to pay the maintenance for the
eight year period ? Assume 6% of
interest.
EGR 312 – Spring ‘05 4

5. 2. The tuition fee in a school are expect to
inflate at the rate of 8%per year and the
tuition at year 1 is P60,000. The parents are
then given a financial planning by the bank
that says they must deposit an amount of
money today that will cover for their child’s
whole 4-year education. If the amount
deposited has an interest rate of 5% per year
compounded annually, how much money
must be deposited to the bank today.
EGR 312 – Spring ‘05 5

6. EGR 312 – Spring ‘05 6
Arithmetic Gradient Factors (P/G, A/G)
To find P for the arithmetic gradient cash flow:
 +
P = $100(P/A,i,4) + $25(P/G,i,4)
$155
$125
$150
$175
0 1 2 3 4 0 1 2 3 4
$155
0 1 2 3 4
$35
$70
$105

7. EGR 312 – Spring ‘05 7
Arithmetic Gradient Factors (P/G, A/G)
To find P for the declining arithmetic
gradient cash flow:
 --
P = $2000(P/A,i,4) - $500(P/G,i,4)
$2000
$1500
$1000
$500
0 1 2 3 4 0 1 2 3 4
$2000
0 1 2 3 4
$500
$1000
$1500

8. EGR 312 – Spring ‘05 8
Arithmetic Gradient Factors (P/G, A/G)
To find the uniform annual series, A, for an arithmetic
gradient cash flow G:

A = G(P/G,i,n) (A/P,i,4)
= G(A/G,i,n)
Where (A/G,i,n) =
0 1 2 3 …
n
G
2G
nG
0 1 2 3 … n
A









1
)
1
(
1
n
i
n
i

9. EGR 312 – Spring ‘05 9
Geometric Gradient Factors (Pg /A)
A Geometric gradient is when the periodic payment is
increasing (decreasing) by a constant percentage:
A1 = $100, g = 0.1
A2 = $100(1+g)
A3 = $100(1+g)2
An = $100(1+g)n-1
$100
$110
$121
$133
0 1 2 3 4

10. EGR 312 – Spring ‘05 10
Geometric Gradient Factors (Pg /A)
To find the Present Worth, Pg , for a geometric gradient
cash flow G:
Pg
$100
$110
$121
$133
0 1 2 3 4
i
g
i
n
A
P
i
g
g
i
i
g
A
P
g
n
g



































1
1
1
1
1
1

11. EGR 312 – Spring ‘05 11
Determining Unknown Interest Rate
To find an unknown interest rate from a single-payment
cash flow or uniform-series cash flow, the following
methods can be used:
1) Use of Engineering Econ. Formulas.
2) Use of factor tables (and interpolation)
3) Spreadsheet (Excel)
a) =IRR(first cell: last cell)
b) =RATE(number_years,A,P,F)

12. EGR 312 – Spring ‘05 12
Determining Unknown Interest Rate
Example: The list price for a vehicle is stated as $25,000.
You are quoted a monthly payment of $658.25 per month
for 4 years. What is the monthly interest rate? What
interest rate would be quoted (yearly interest rate)?
Using factor table:
$25000 = $658.25(P/A,i,48)
37.974 = (P/A,i,48)
i = 1% from table 4, pg 705
0r 12% annually

13. EGR 312 – Spring ‘05 13
Determining Unknown Interest Rate
Example: The list price for a vehicle is stated as $25,000.
You are quoted a monthly payment of $658.25 per month
for 4 years. What is the monthly interest rate? What
interest rate would be quoted (yearly interest rate)?
Using formula:
Use Excel trial and error method to find i.











 48
48
)
1
(
1
i)
(1
$658.25
$25000
i
i











 48
48
)
1
(
1
i)
(1
37.9795
i
i

14. EGR 312 – Spring ‘05 14
Determining Unknown Number of Periods (n)
To find an unknown number of periods for a single-
payment cash flow or uniform-series cash flow, the
following methods can be used:
1) Use of Engineering Econ. Formulas.
2) Use of factor tables
3) Spreadsheet (Excel)
a) =NPER(i%,A,P,F)

15. EGR 312 – Spring ‘05 15
Determining Unknown Number of Periods (n)
Example: Find the number of periods required such that
an invest of $1000 at 5% has a future worth of $5000.
P = F(P/F,5%,n)
$1000 = $5000(P/F,5%,n)
0.2 = (P/F,5%,n)
n ~ 33 periods