1) Interest is the amount paid for using borrowed money or the income earned from money that has been loaned. Simple interest is calculated using only the principal amount and ignores interest earned in previous periods. 2) Compound interest differs in that the interest earned is added to the principal amount and also earns interest in subsequent periods, allowing the total to grow more quickly over time. 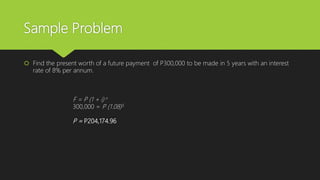3) Examples show calculations for simple and compound interest rates as well as determining present worth values given future amounts, interest rates, and time periods.

1. PRINCIPLES OF INTEREST AND
MONEY-TIME RELATIONSHIP

2. INTEREST
Interest is the amount of money paid
for the use of borrowed capital or the
income produced by money which has
been loaned.

3. SIMPLE INTEREST
I = Pin
F = P + I
F = P(1+in)
Simple Interest is calculated using the principal only, ignoring any interest
that had been accrued in preceding periods. In practice, simple interest is
paid on short-term loans in which the time of the loan is measured in days.
where: I = interest
P = principal or present worth
n = number of interest periods
i = rate of interest per interest period
F = accumulated amount or future worth

4. SIMPLE INTEREST
Ordinary Simple Interest (OSI)
 One month is equal to 30 days
 One year is 360 days
Exact Simple Interest (ESI)
 Based on the exact number of days per
month
 365 days per year
 366 days for leap year

5. DISCOUNT
Discount on a negotiable paper
is the difference between the
present worth (the amount
received for the paper in cash)
and the worth of the paper at
sometime in the future (the face
value of the paper or principal).
Discount is interest paid in
advance.
Discount = Future Worth – Present Worth
D = F - P
d = rate of discount
d = Discount
Principal
i = d
1 - d

6. Sample Problem
 A man borrowed P2,000 from a bank and promised to pay the amount for one year. He received
only the amount of P1,920 after the bank collected an advance interest of P80.00. What was the
rate of discount and the rate of interest that the bank collected in advance?
Rate of discount = 80 x 100
2000
= 0.04 or 4%
Rate of interest= 80 x 100
1920
= 0.0417 or 4.17%

7. Sample Problem
 If you borrowed money from your friend with simple interest of 12%, find the present worth of
P50,000; which due at the end of 7 months.
F = P + I
F = P + Pin
F = P (1 + in)
P = F = 50,000
(1+in) [1+0.12(7/12)]
= P46,728.97

8. Sample Problem
 A price tag of P1,200 is payable in 60 days but if paid with in 30 days it will have a 3% discount.
Find the rate of interest.
 A bank charges 12% simple interest on a P300 loan. How much will be repaid if the loan is paid
back in one lump sum after three years?
 P5,000 is borrowed for 75 days at 16% per annum simple interest. How much will be due at the
end of 75 days?
 If you borrow money from your friend with simple interest of 12%, find the present worth of
P20,000, which is due at the end of 9 months.

9. COMPOUND INTEREST
 The interest earned by the principal which is added to the principal will also earn an interest for
the succeeding period.
 The interest on top of interest
F = P (1 + i) n
INTEREST
PERIOD
PRINCIPAL INTEREST COMPOUND AMOUNT
1 P Pi P + Pi
2 P(1+i) P(1+i)i P(1+i) + P(1+i)i = P(1+i)2
3 P(1+i)2 P(1+i)2 i P(1+i)2 + P(1+i)2 i = P(1+i)3
P = present worth or principal i = rate of interest
F = compound amount at the end of “n” periods n = no. of periods

10. COMPOUND INTEREST
 For 8% compounded annually in 5 yrs.
i = 0.08 n = 5 periods
 For 8% compounded semi-annually in 5 yrs.
i = 0.08 = 0.04 n = 5(2) = 10 periods
2
 For 8% compounded quarterly in 5 yrs.
i = 0.08 = 0.02 n = 5(4) = 20 periods
4
 For 8% compounded monthly in 5 yrs.
i = 0.08 = 0.00667 n = 5(12) = 60 periods
12
 For 8% compounded bimonthly in 5 yrs.
i = 0.08 = 0.013 n = 5(6) = 30 periods
6

11. Sample Problem
 Find the present worth of a future payment of P300,000 to be made in 5 years with an interest
rate of 8% per annum.
F = P (1 + i) n
300,000 = P (1.08)5
P = P204,174.96

12. Sample Problem
 How long will it take money to double itself if invested at 5% compounded annually?
 Find the present worth of a future payment of P100,000 to be made in 10 years with an interest of
12% compounded quarterly