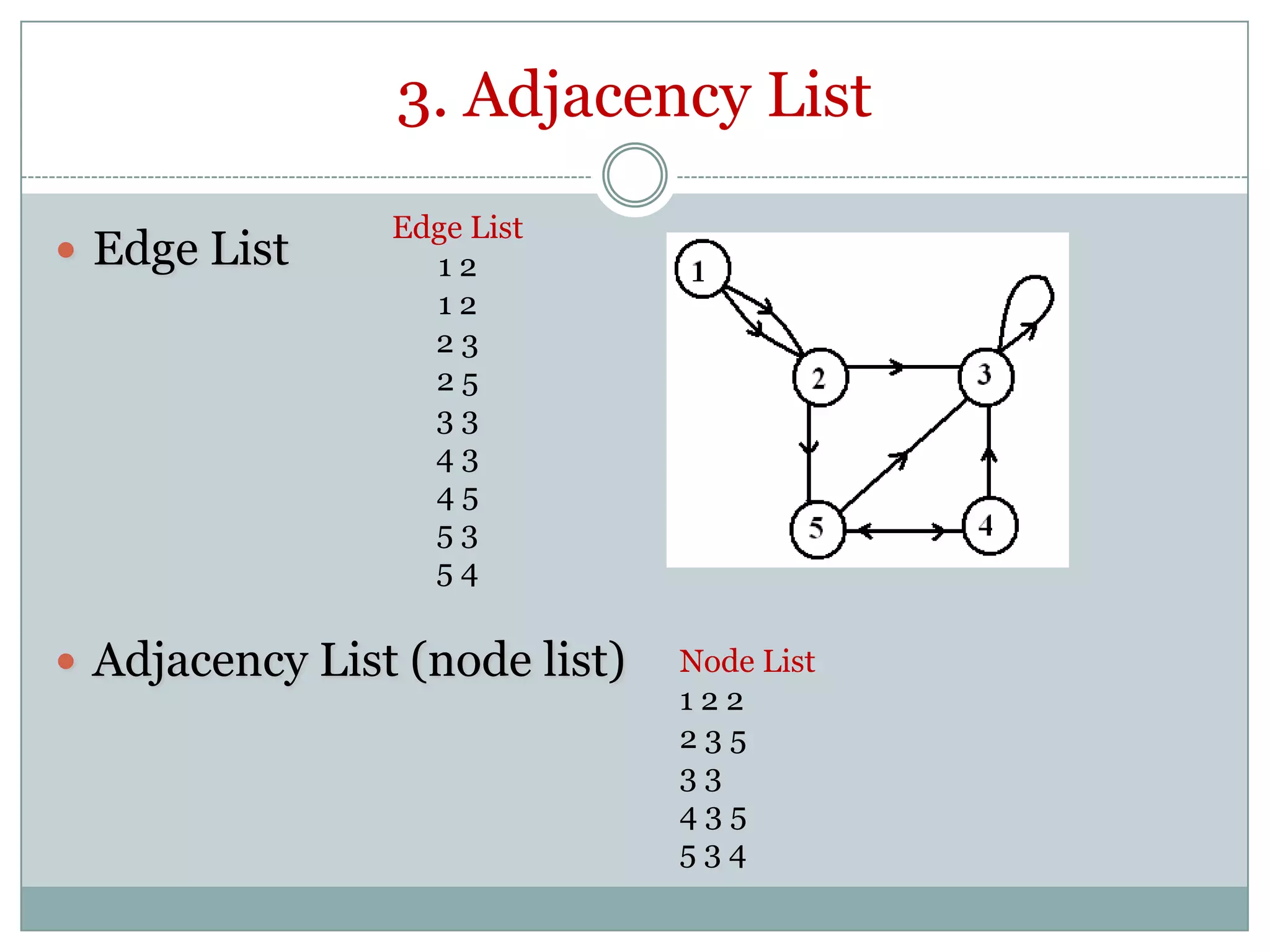
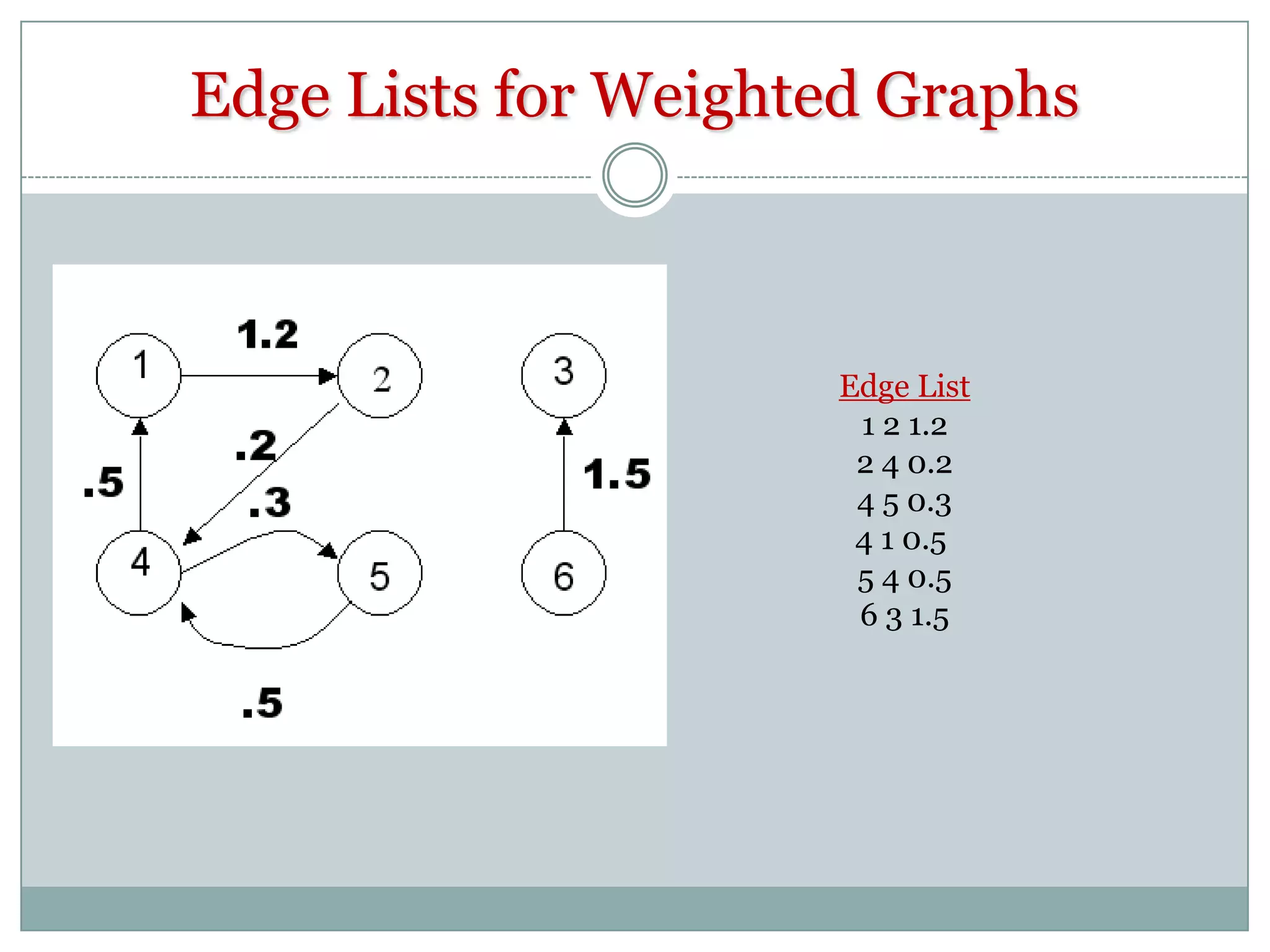
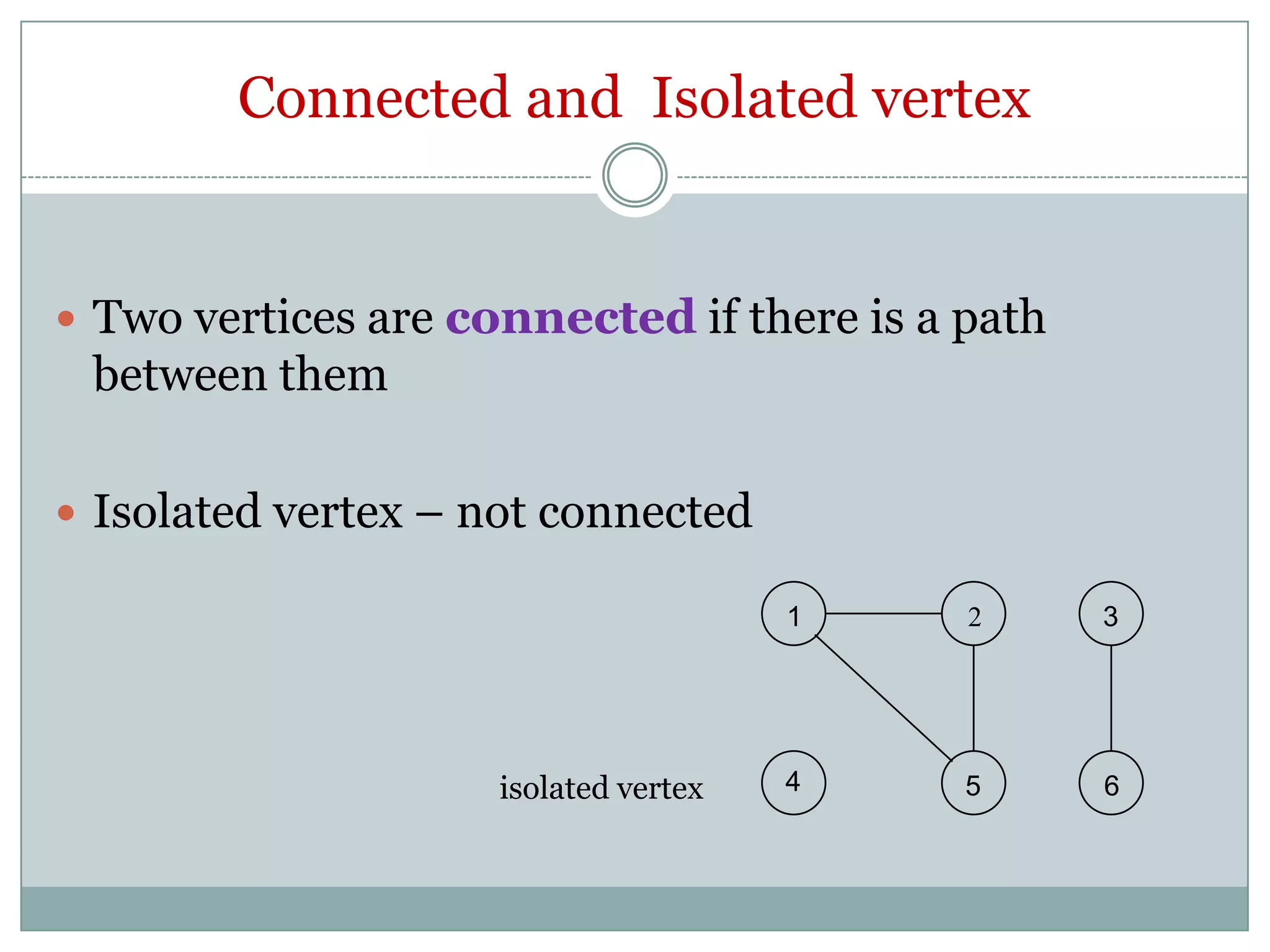
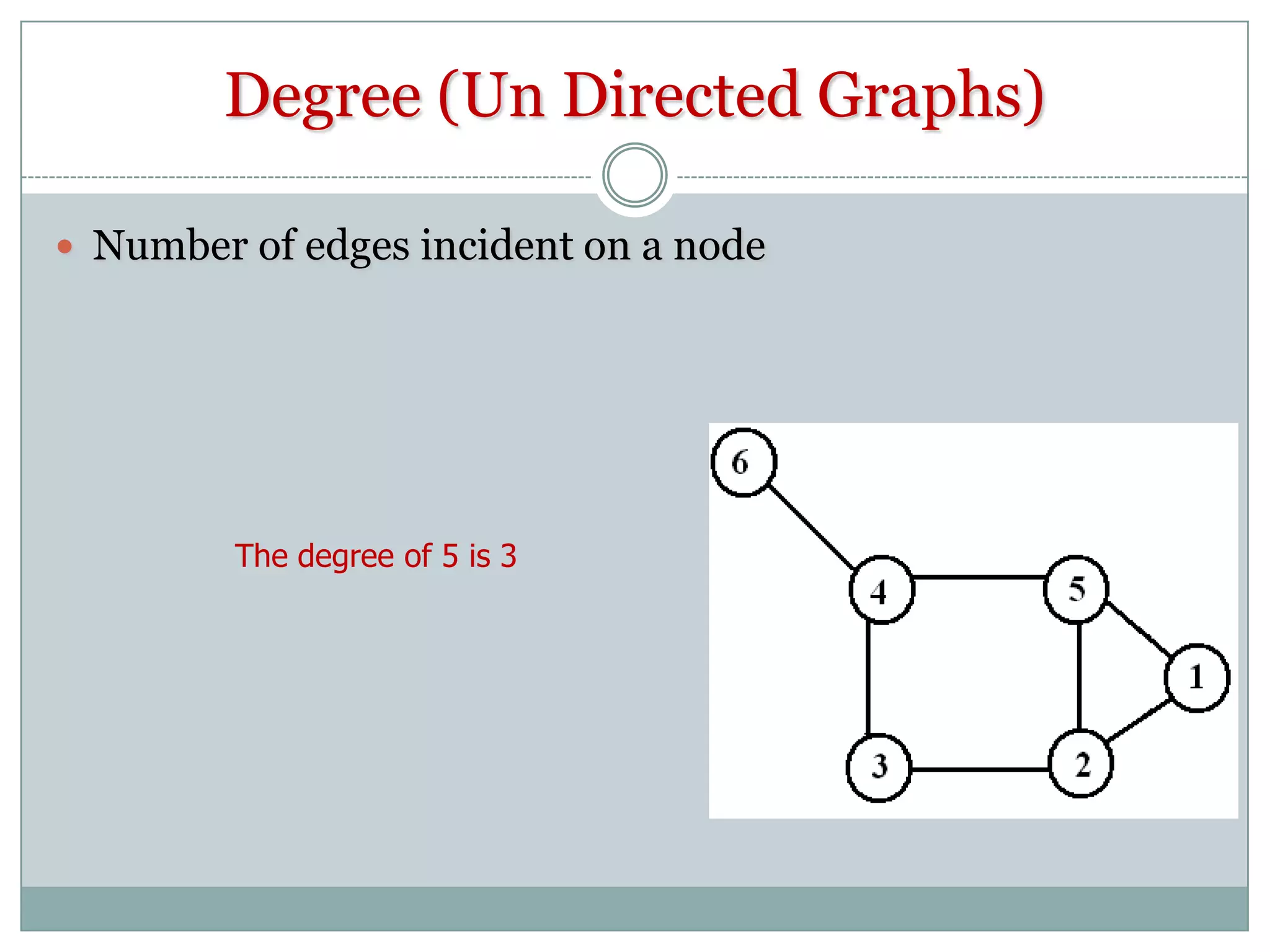
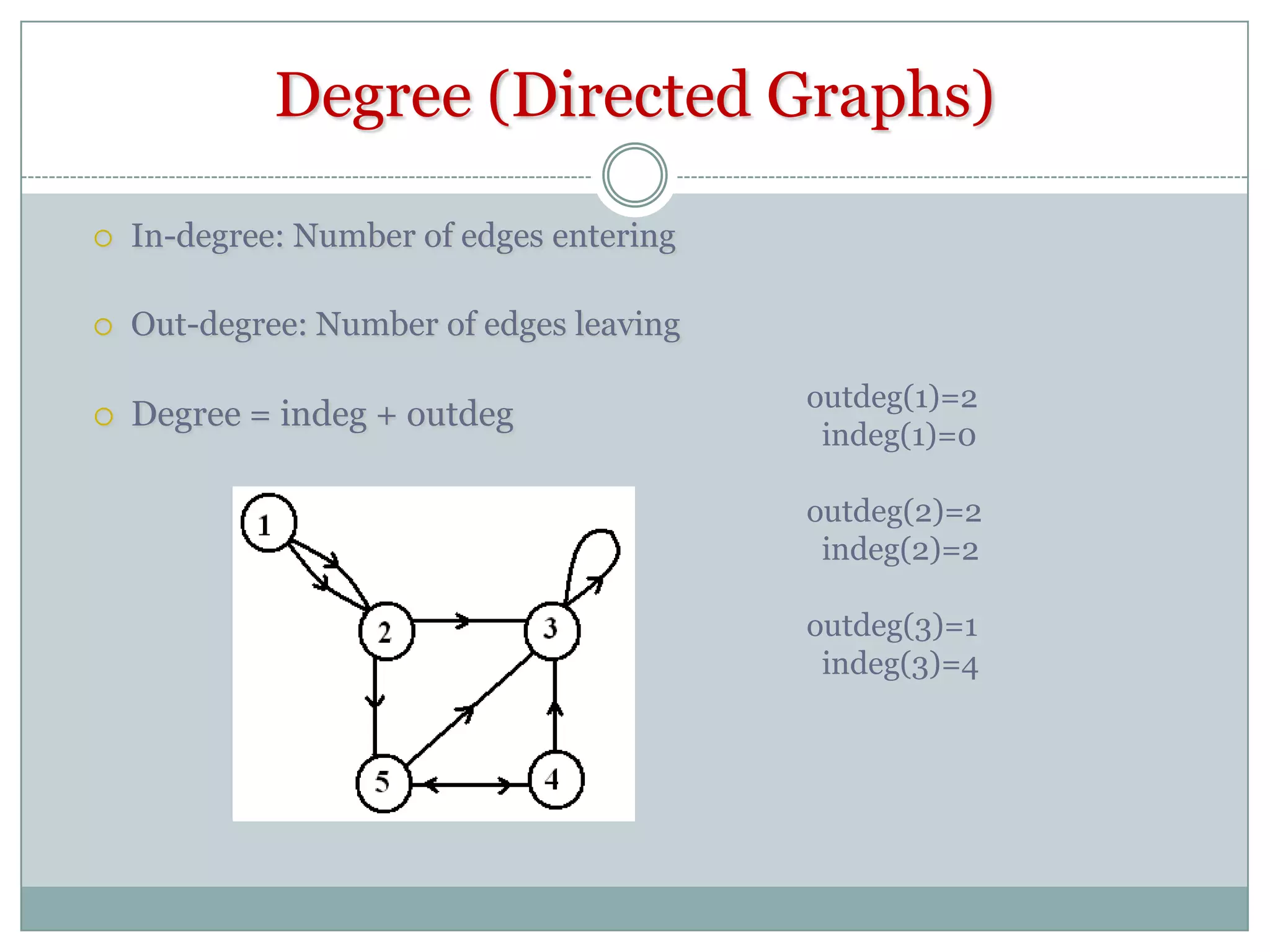
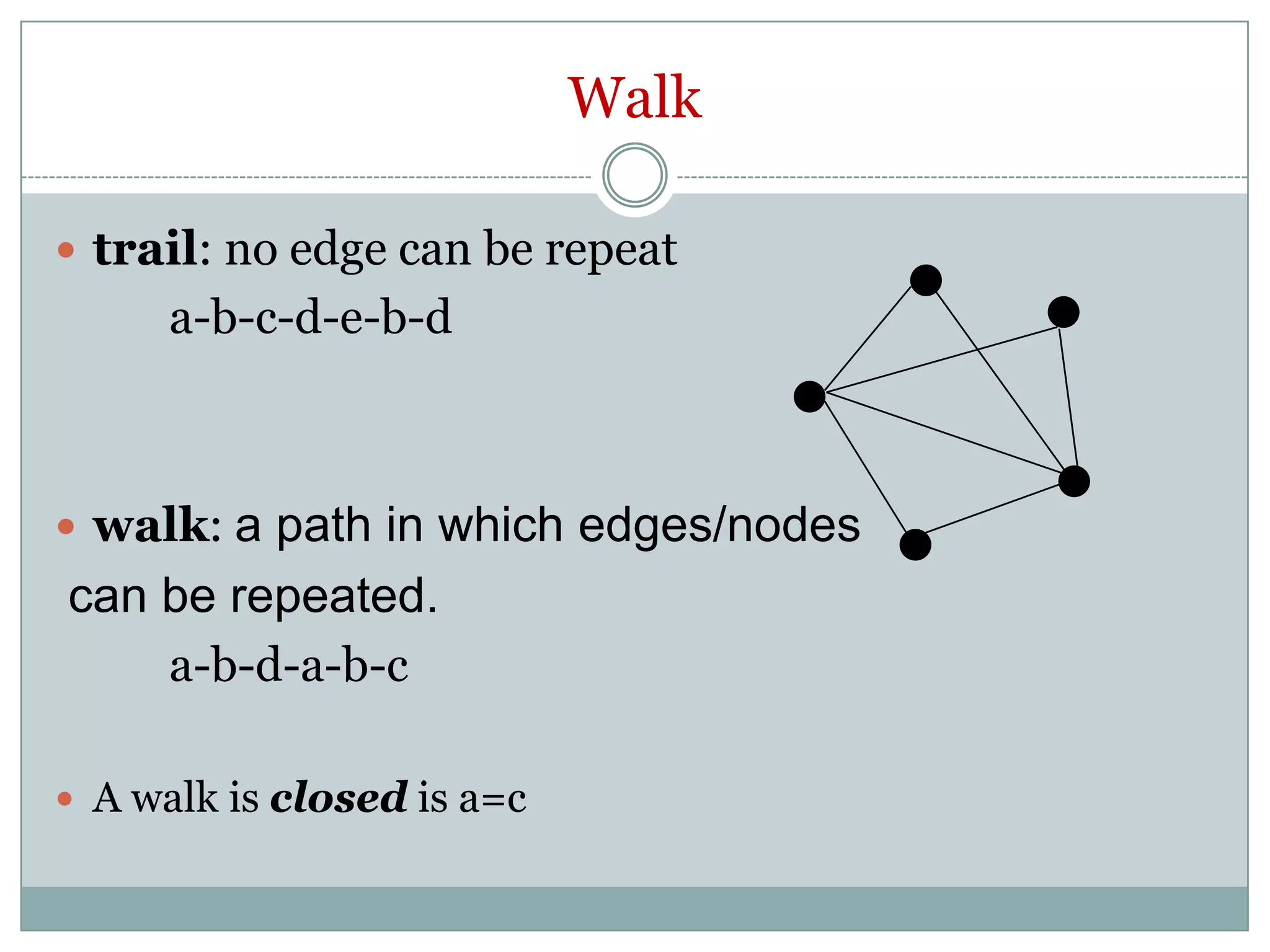
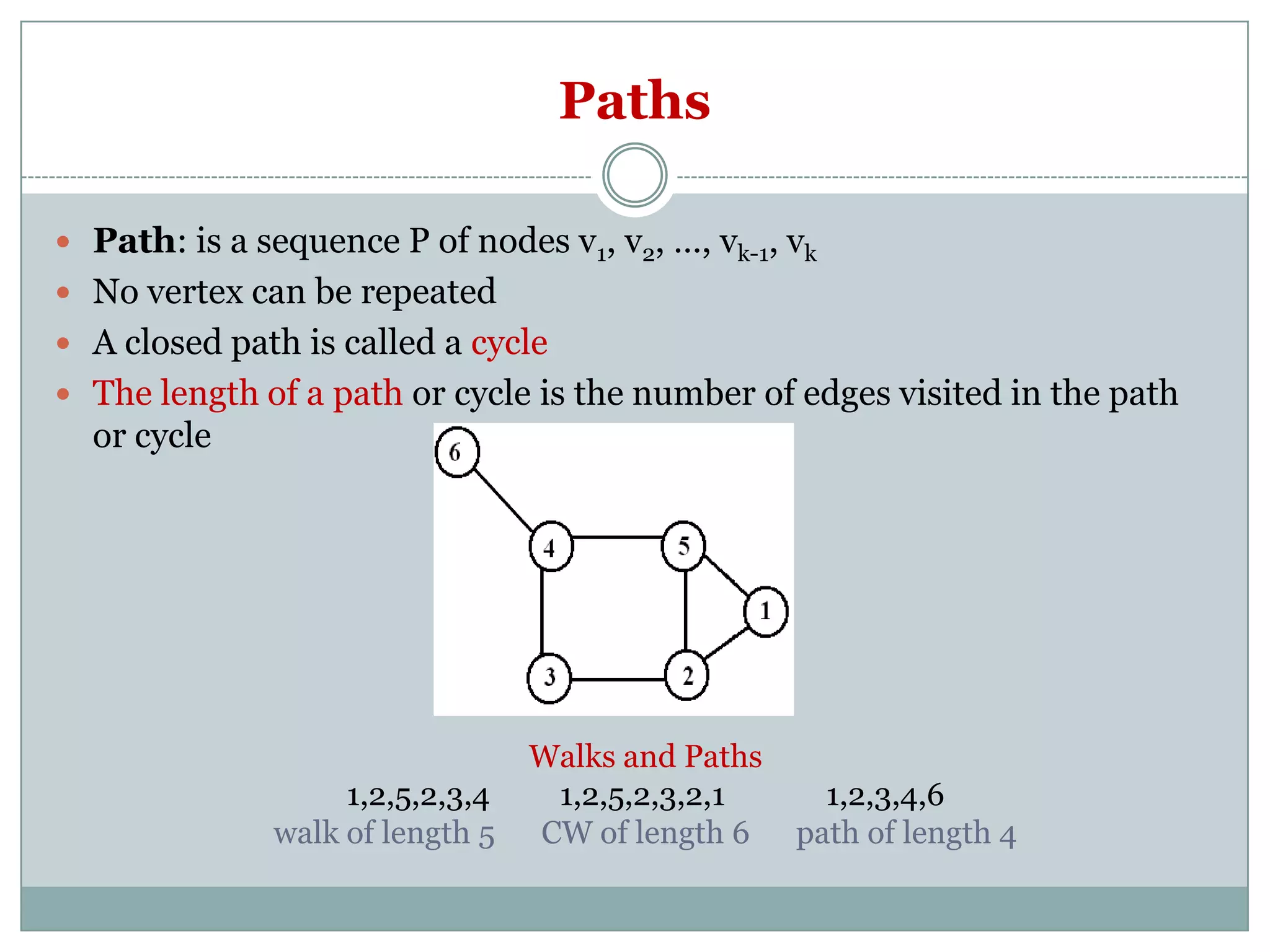
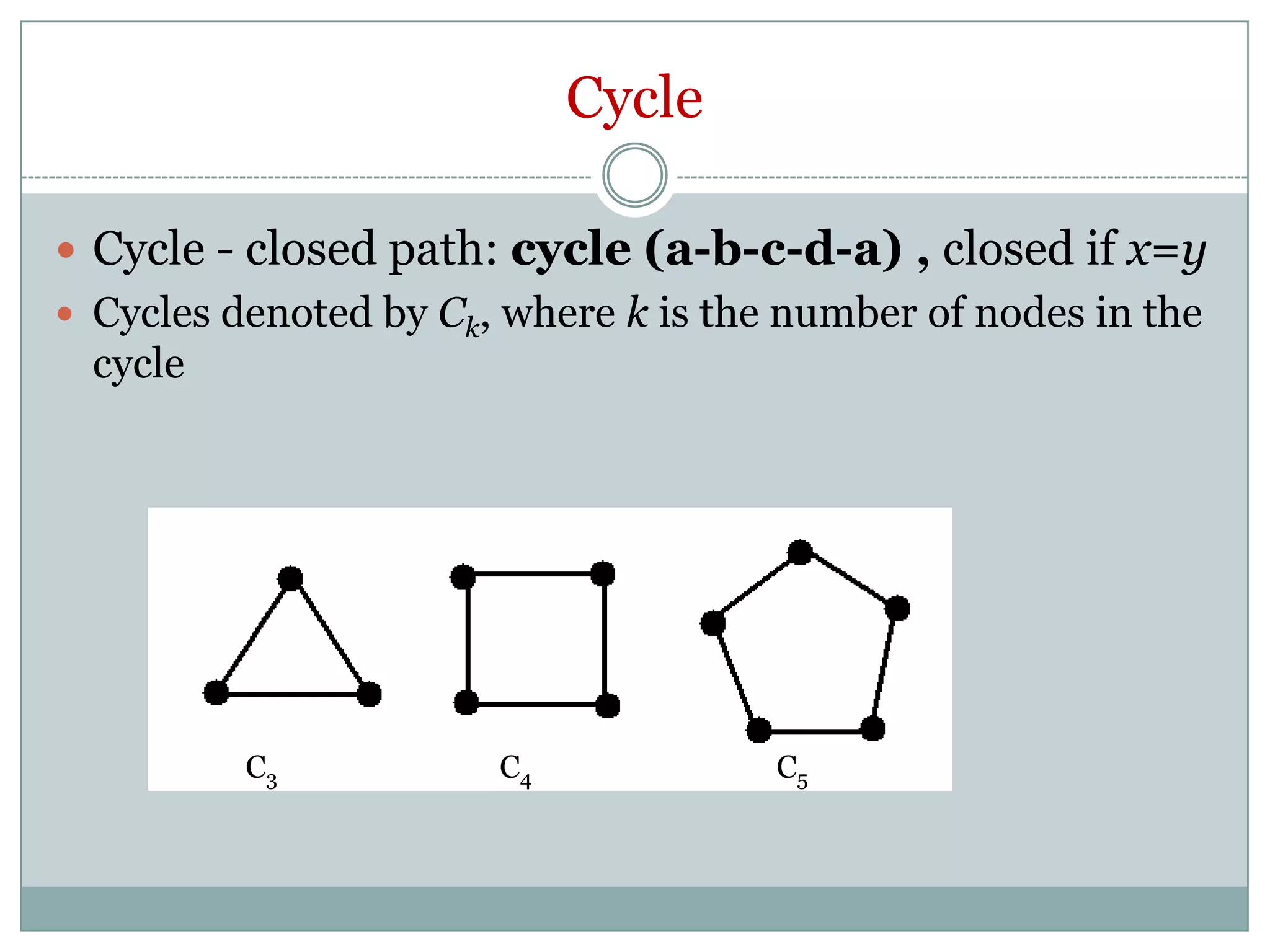
The document provides an introduction to graph theory. It begins with a brief history, noting that graph theory originated from Euler's work on the Konigsberg bridges problem in 1735. It then discusses basic concepts such as graphs being collections of nodes and edges, different types of graphs like directed and undirected graphs. Key graph theory terms are defined such as vertices, edges, degree, walks, paths, cycles and shortest paths. Different graph representations like the adjacency matrix, incidence matrix and adjacency lists are also introduced. The document is intended to provide an overview of fundamental graph theory concepts.














![2. Incidence Matrix
VxE
[vertex, edges] contains the edge's data
1, 2
1,5
2 ,3
2 ,5
3, 4
4 ,5
4 ,6
1
1
1
0
0
0
0
0
2
1
0
1
1
0
0
0
3
0
0
1
0
1
0
0
4
0
0
0
0
1
1
1
5
0
1
0
1
0
1
0
6
0
0
0
0
0
0
1](https://image.slidesharecdn.com/1introductiontographtheory-140220082526-phpapp02/75/Introduction-to-Graph-Theory-22-2048.jpg)