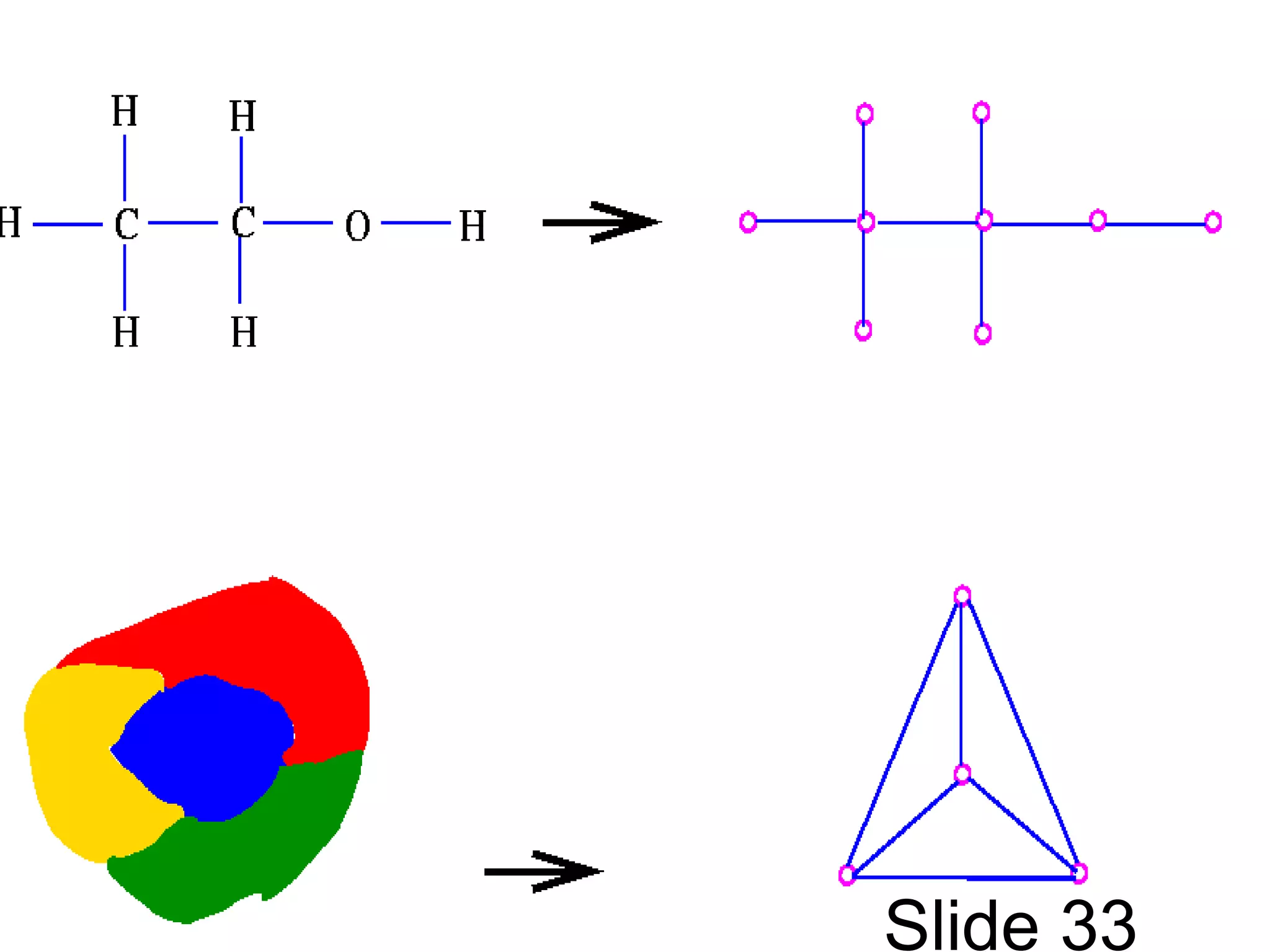
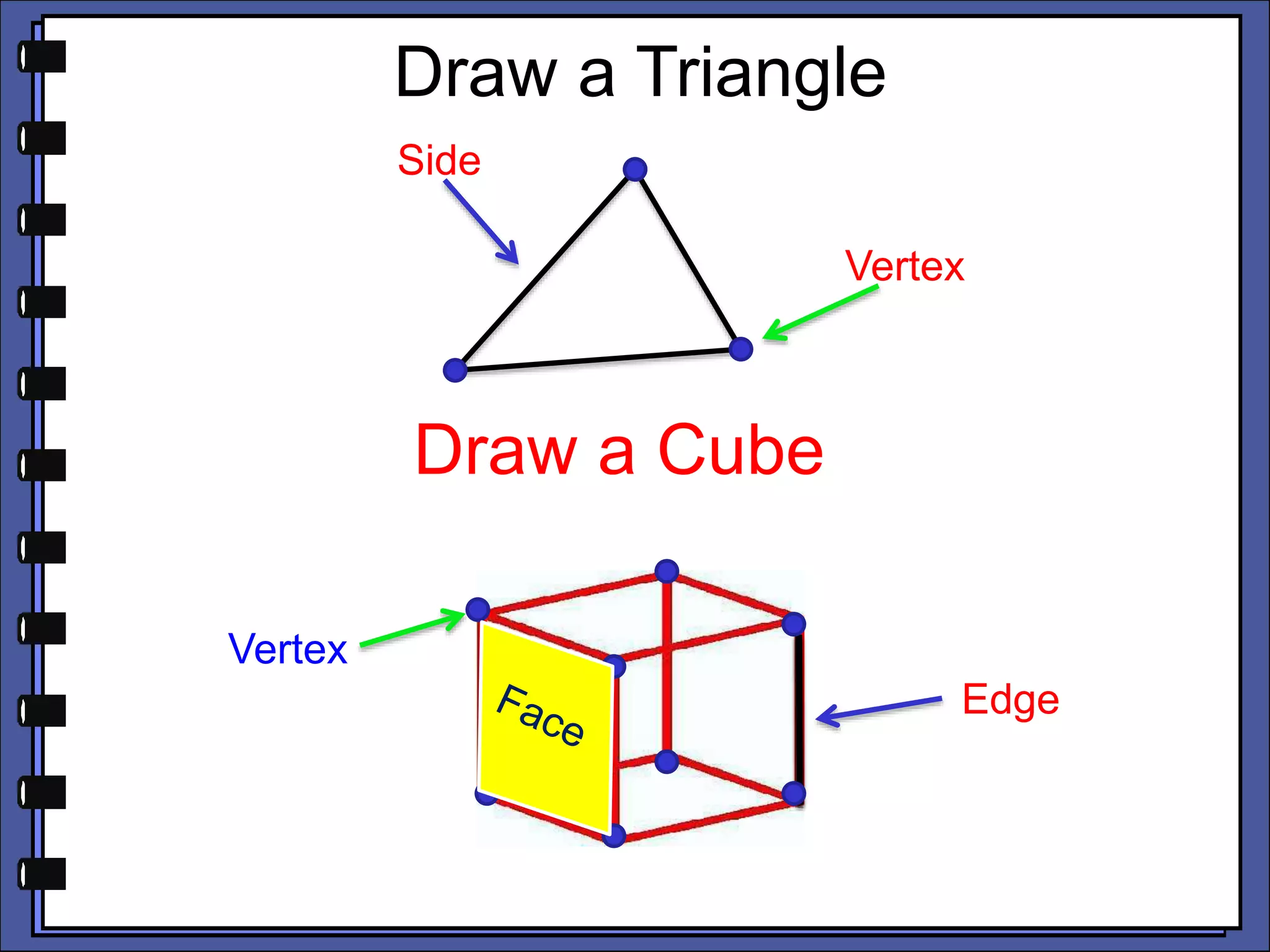
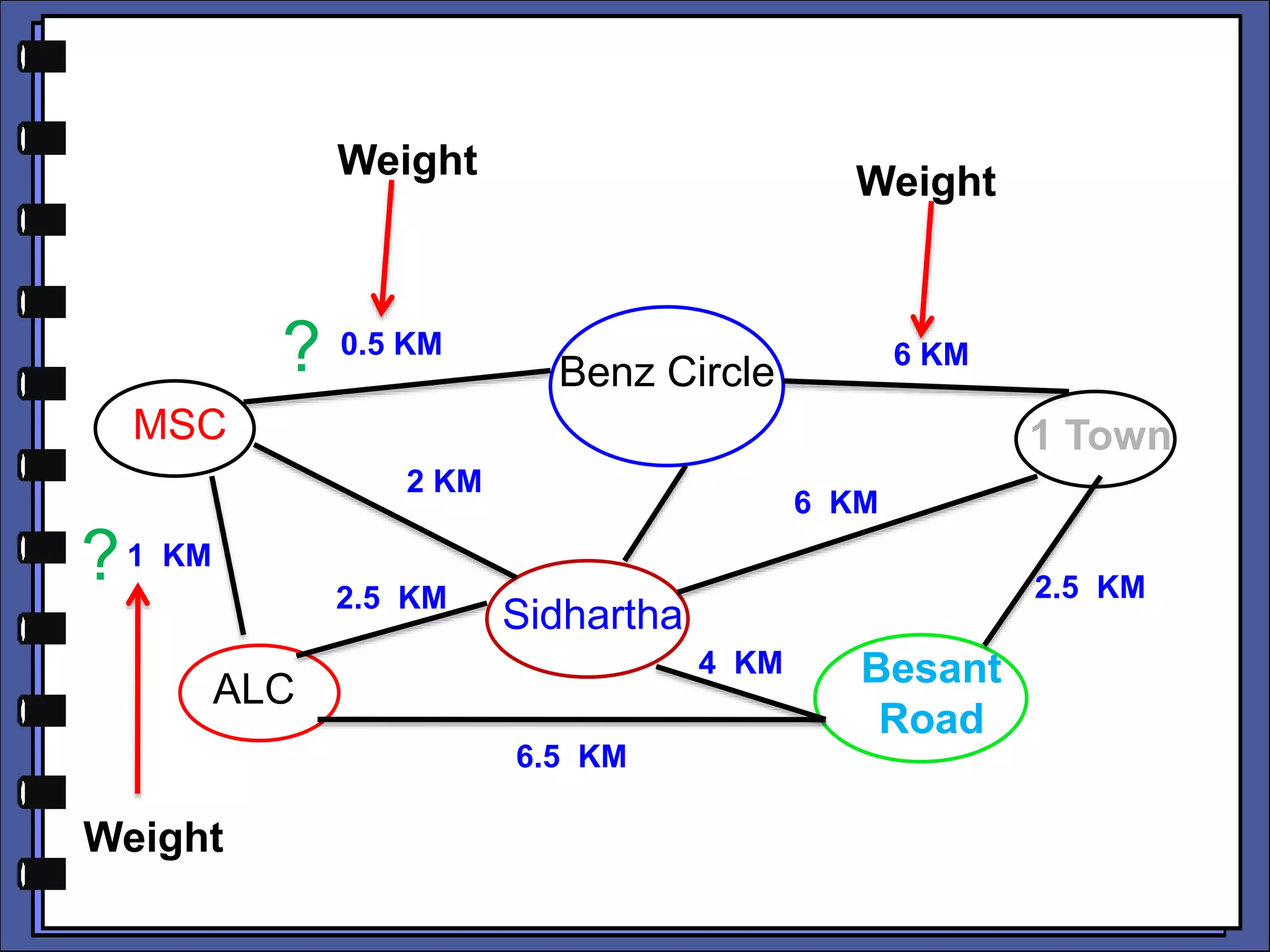
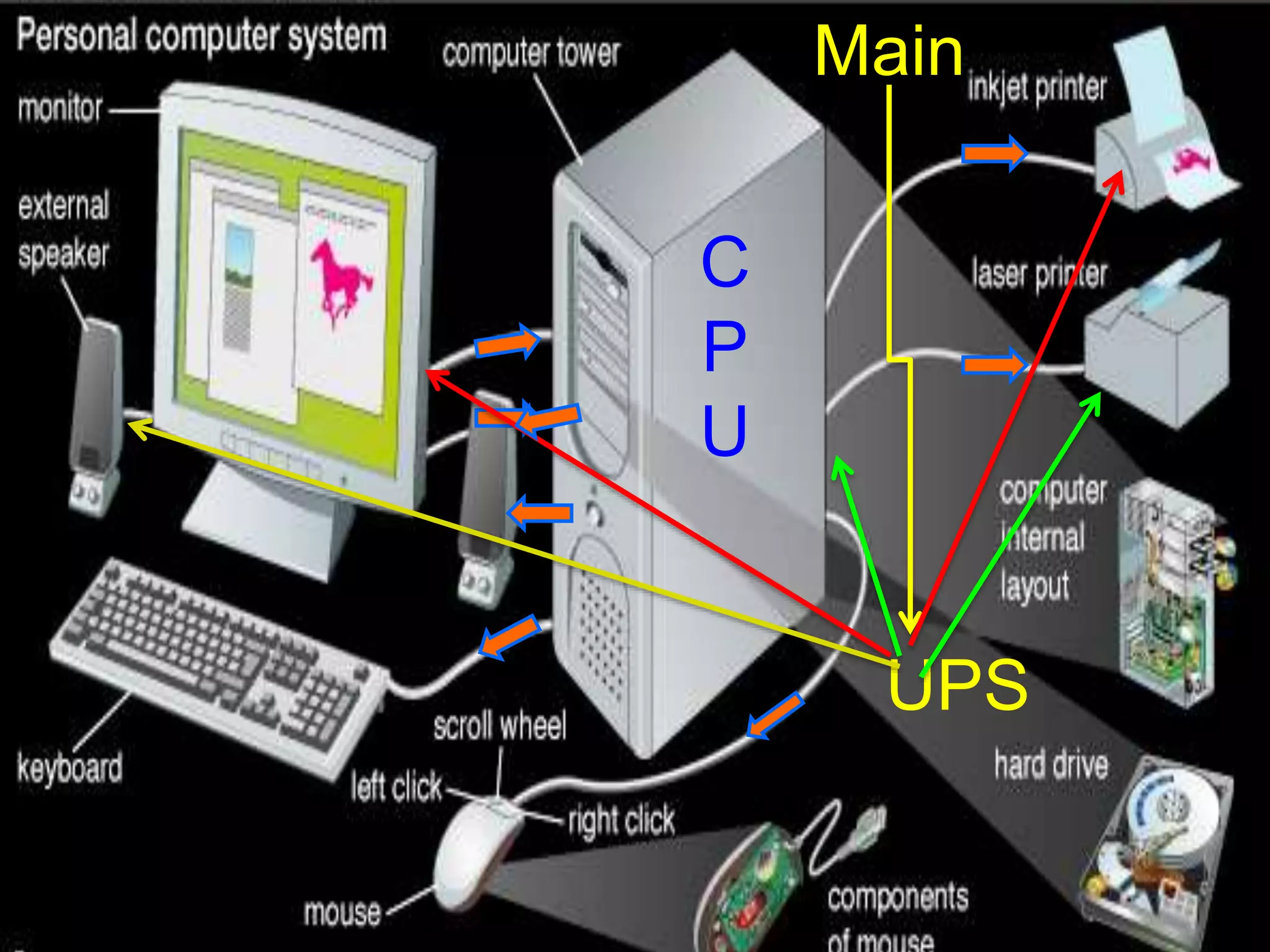
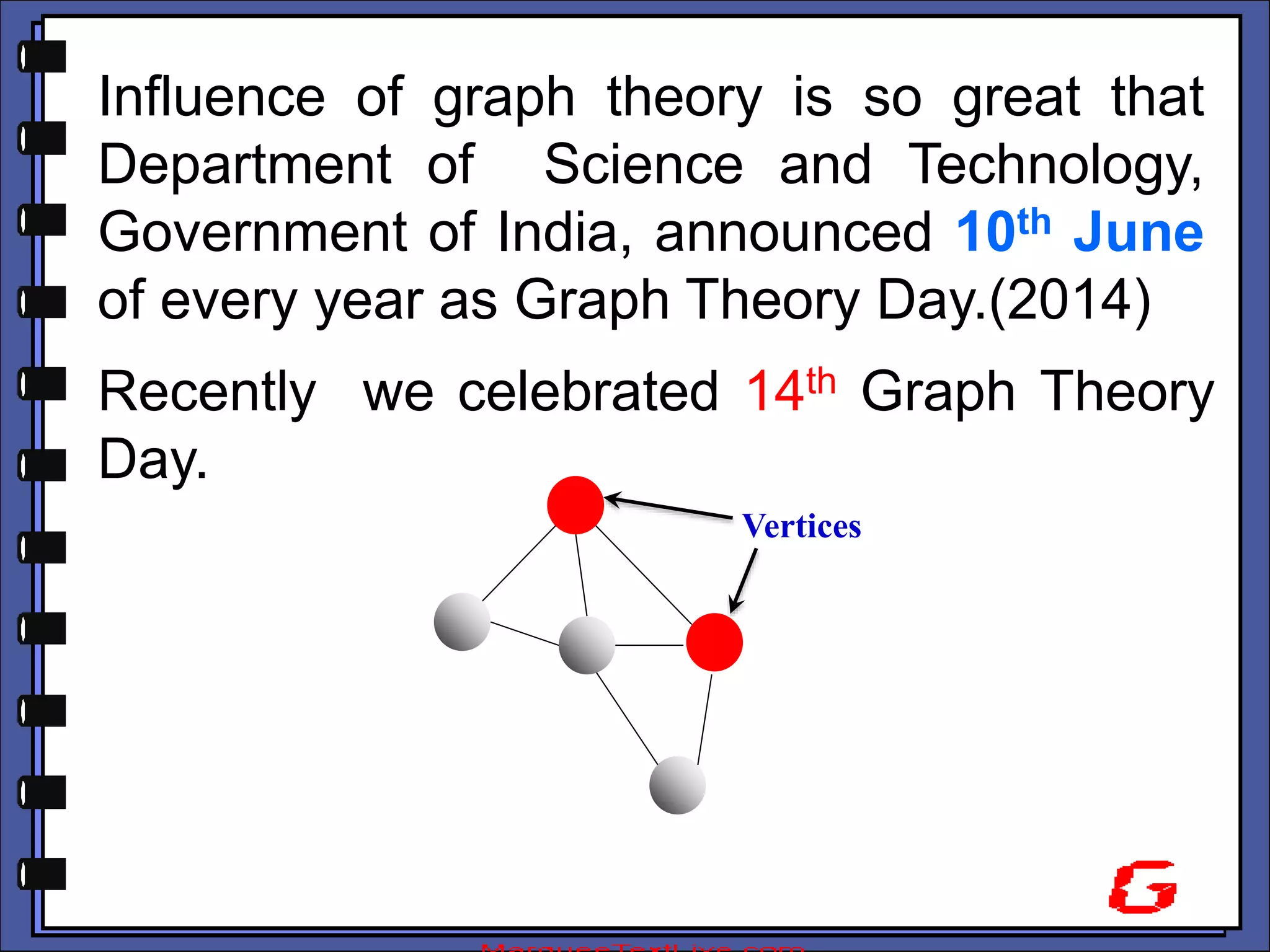
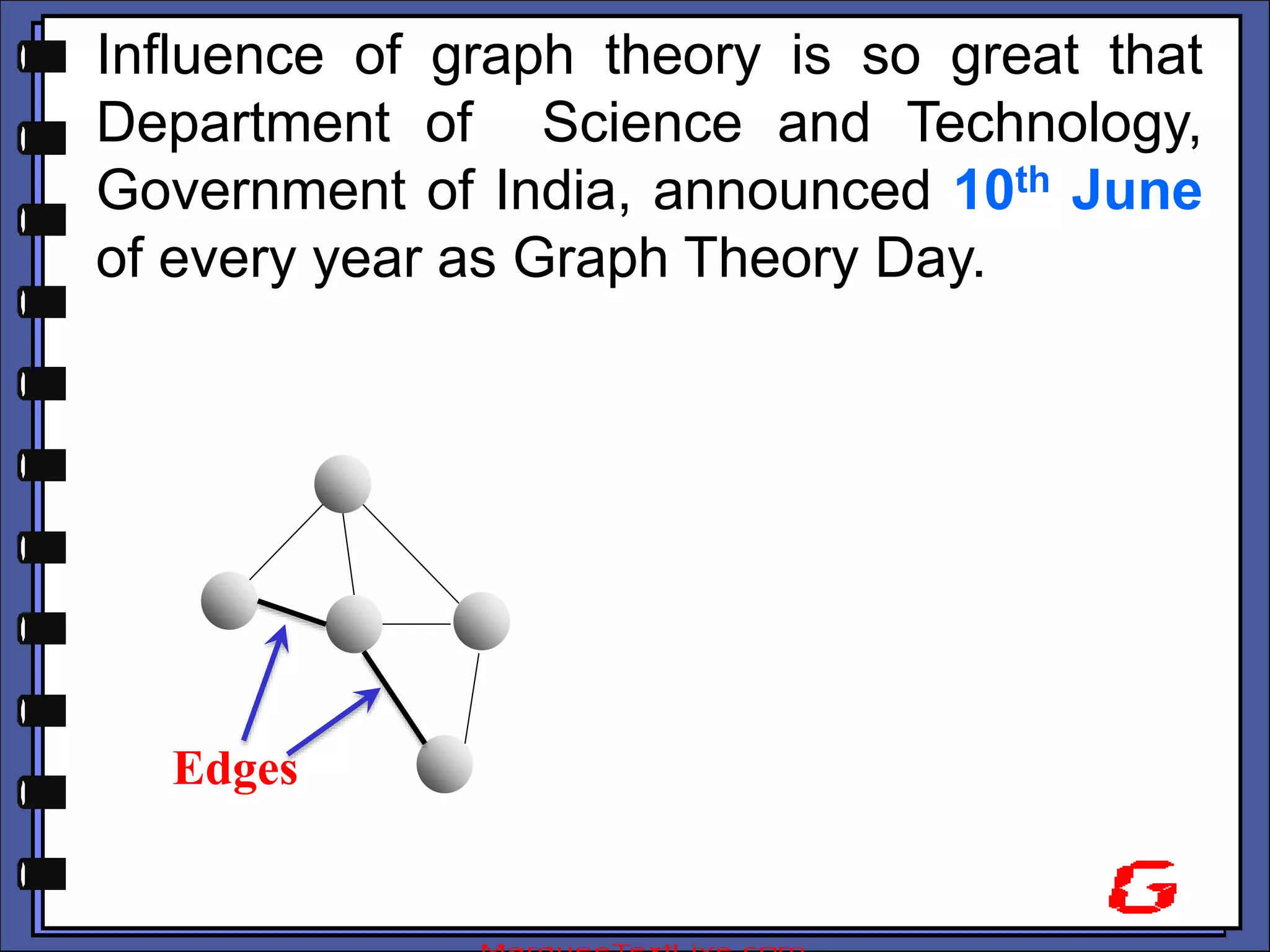
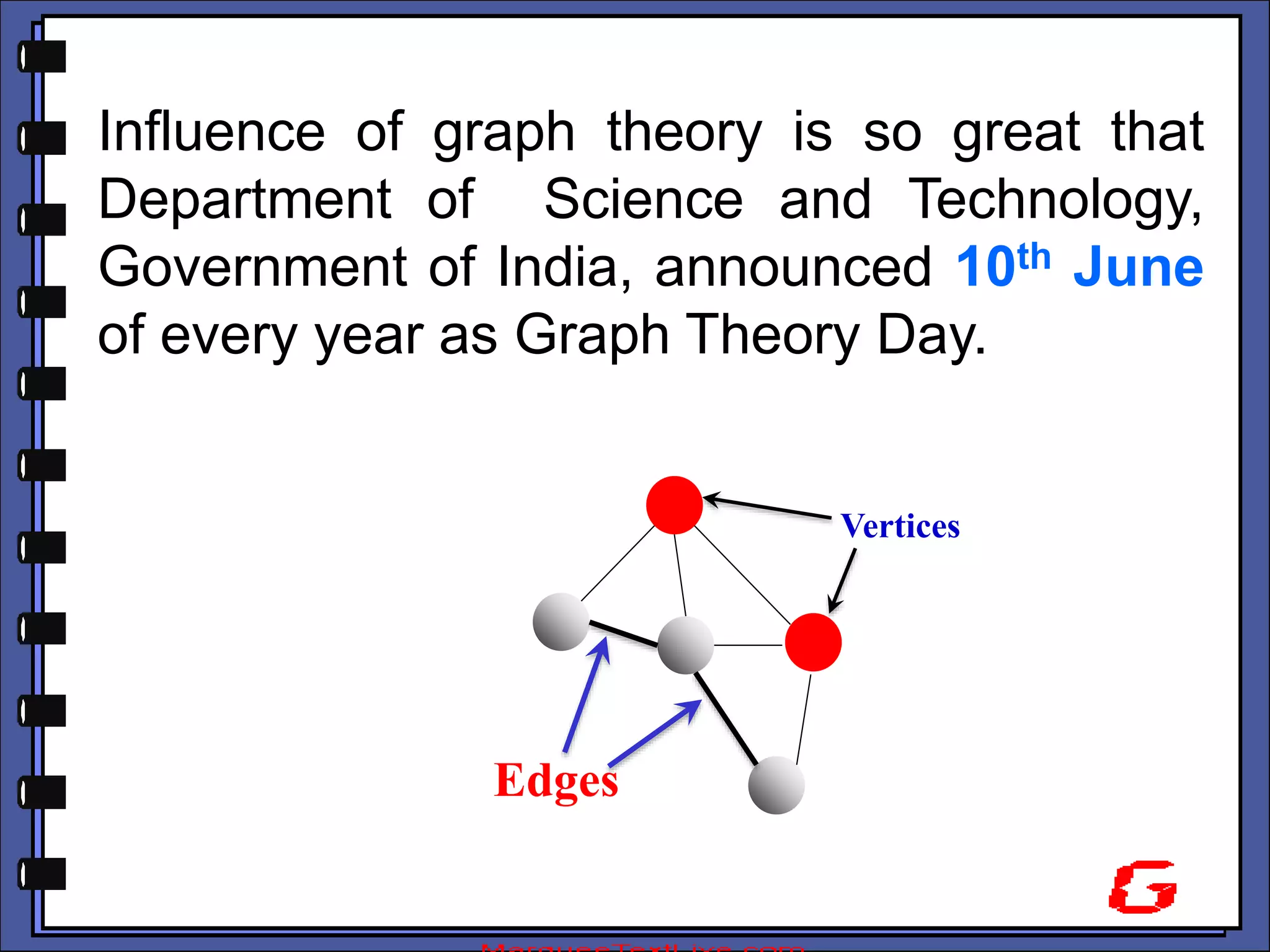
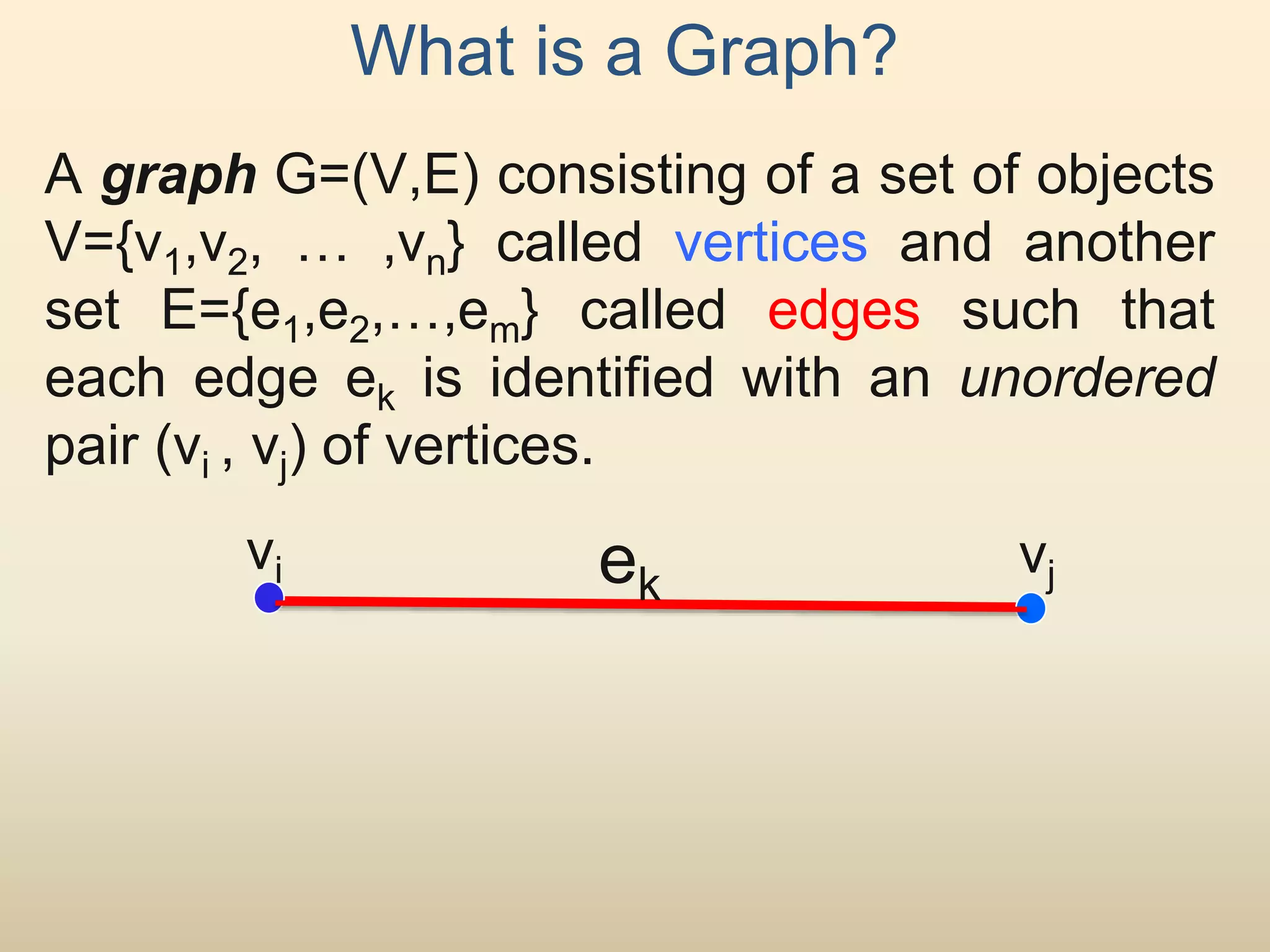
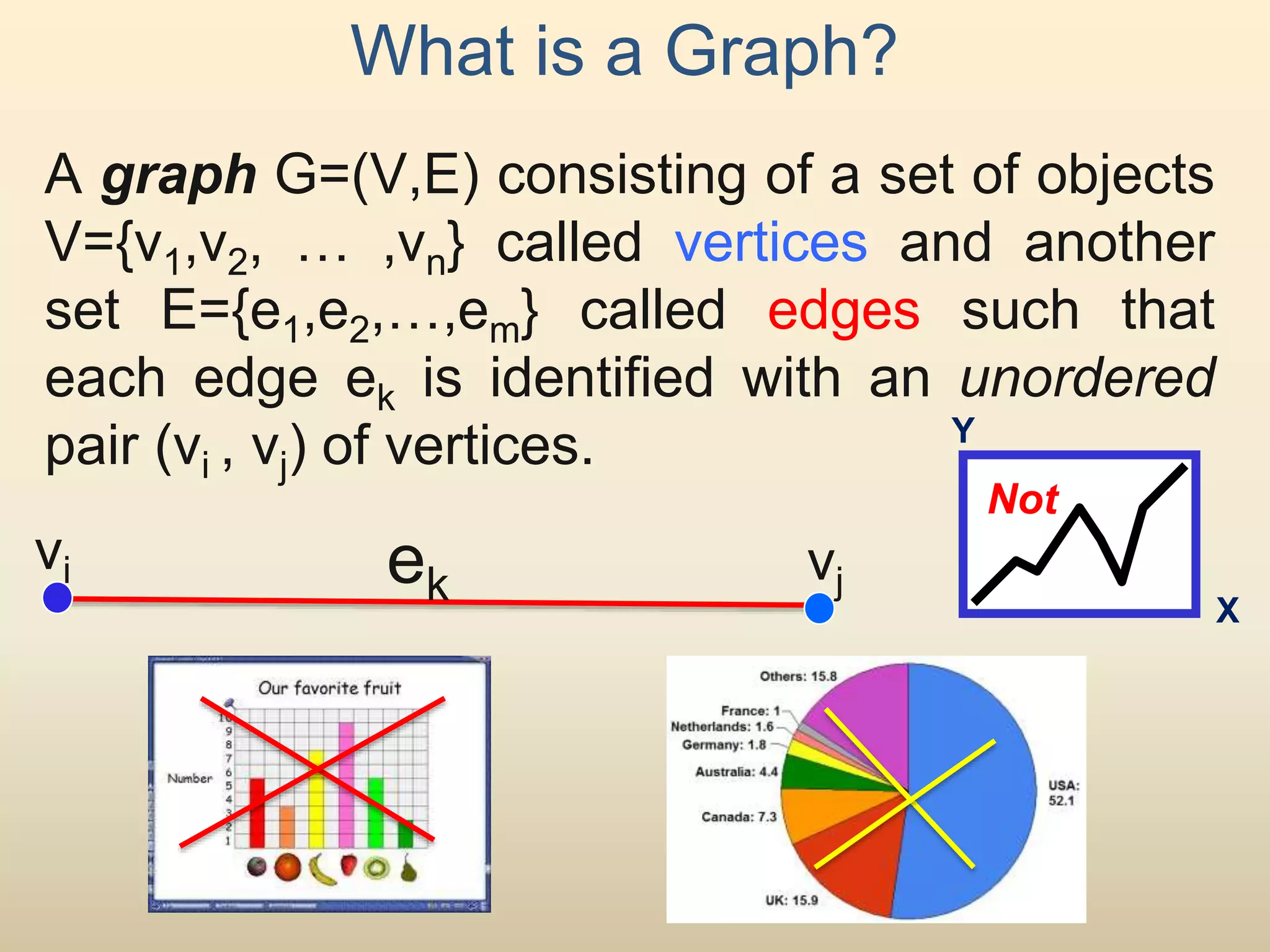
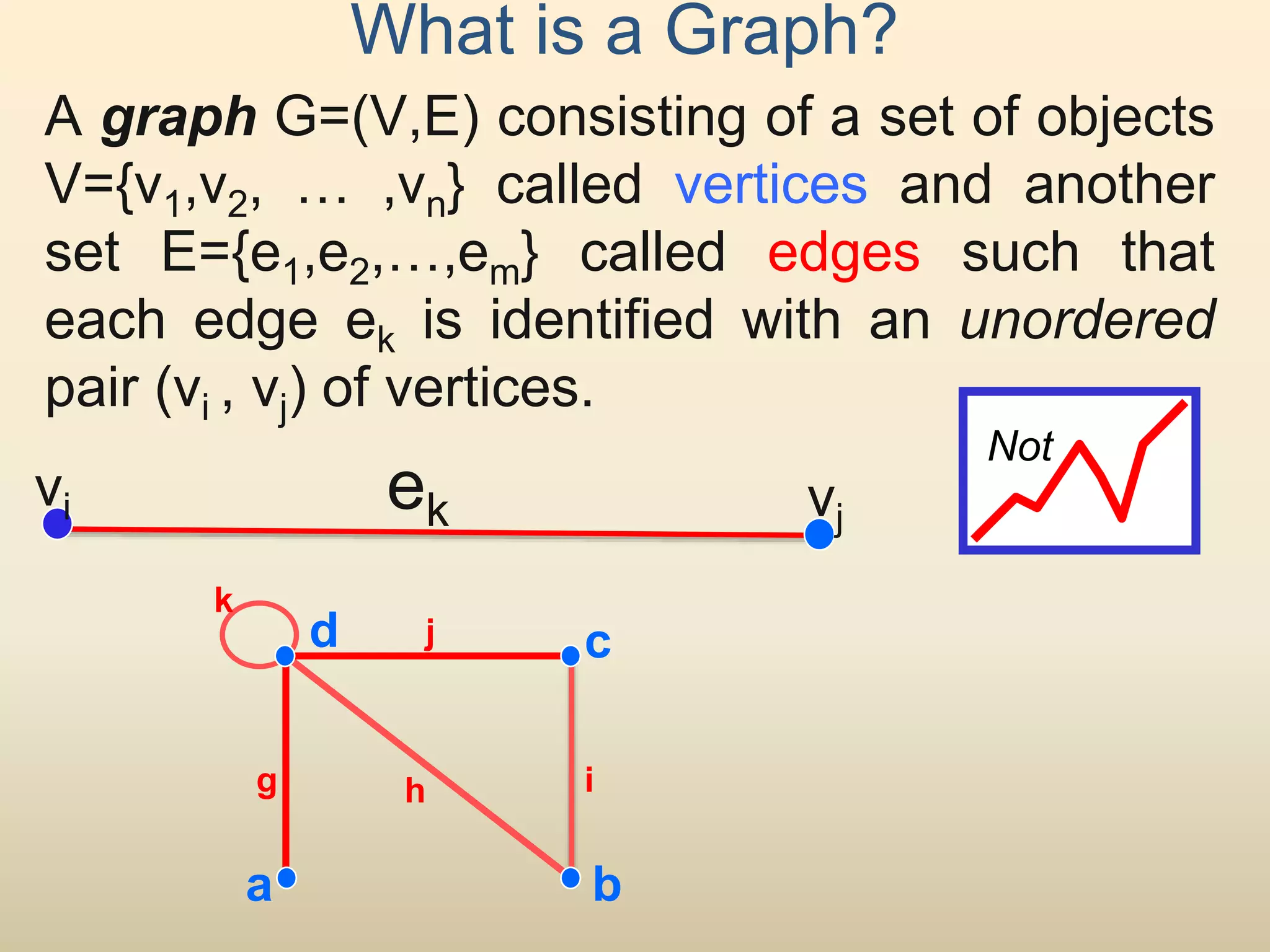
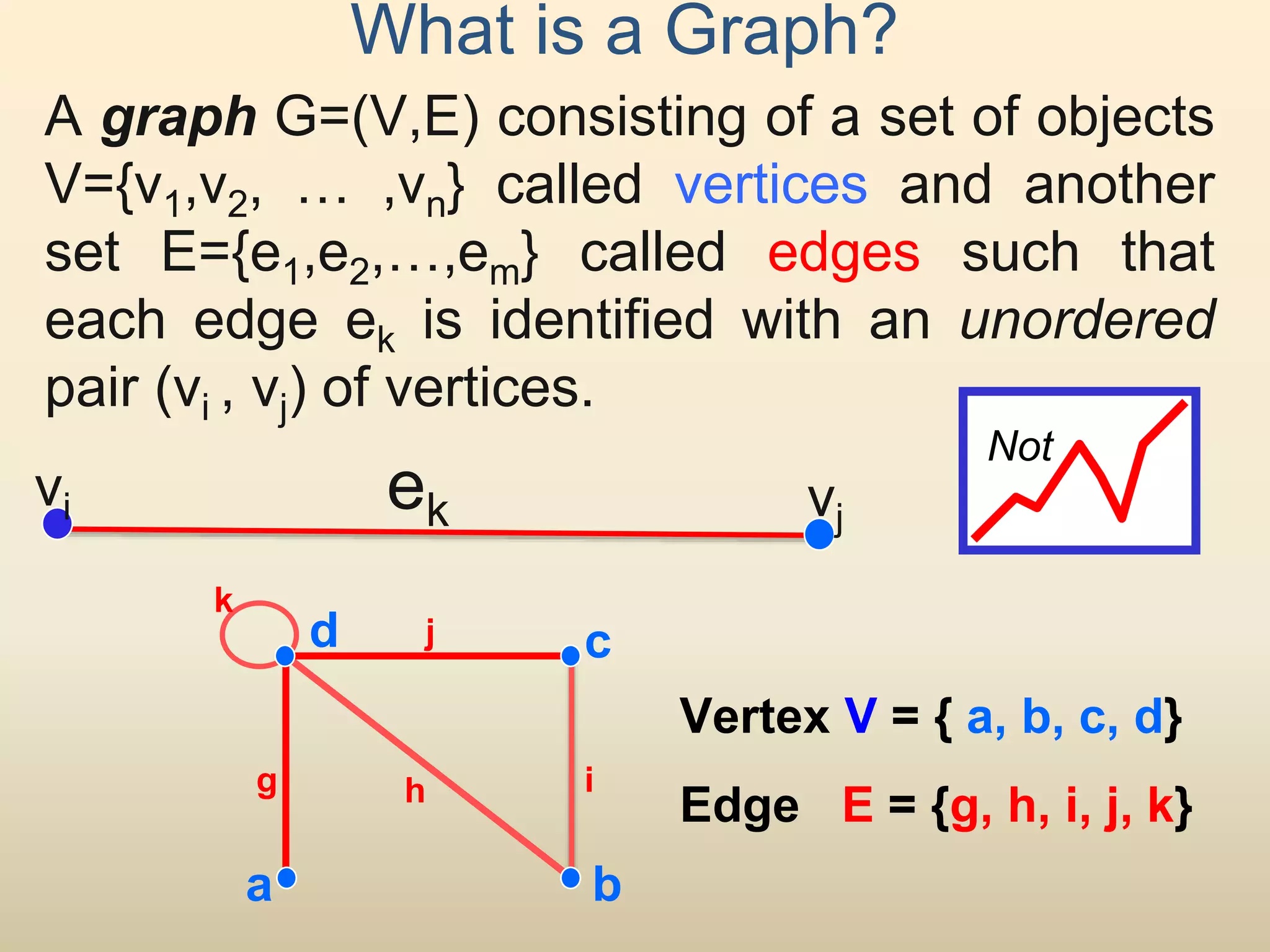
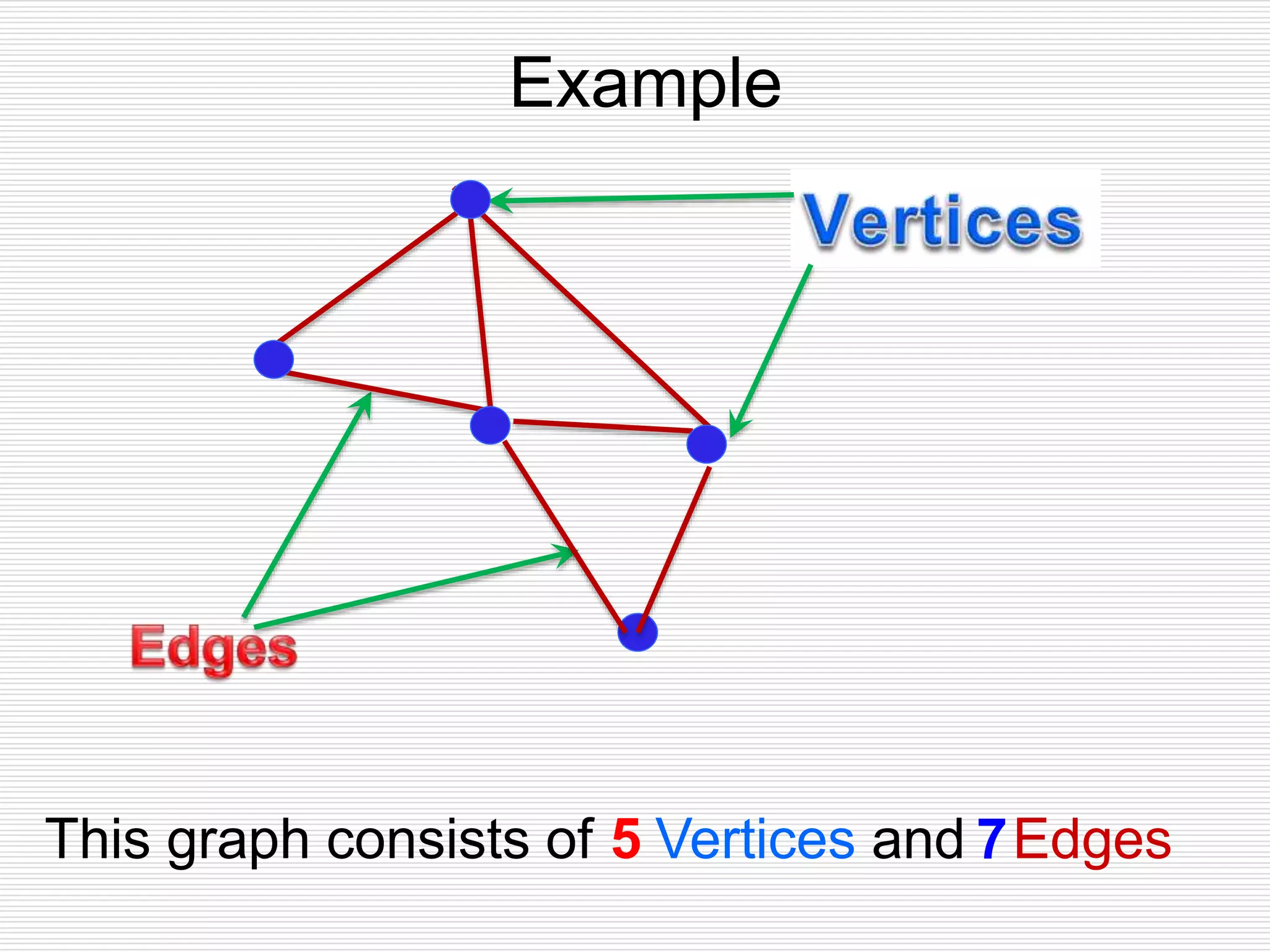
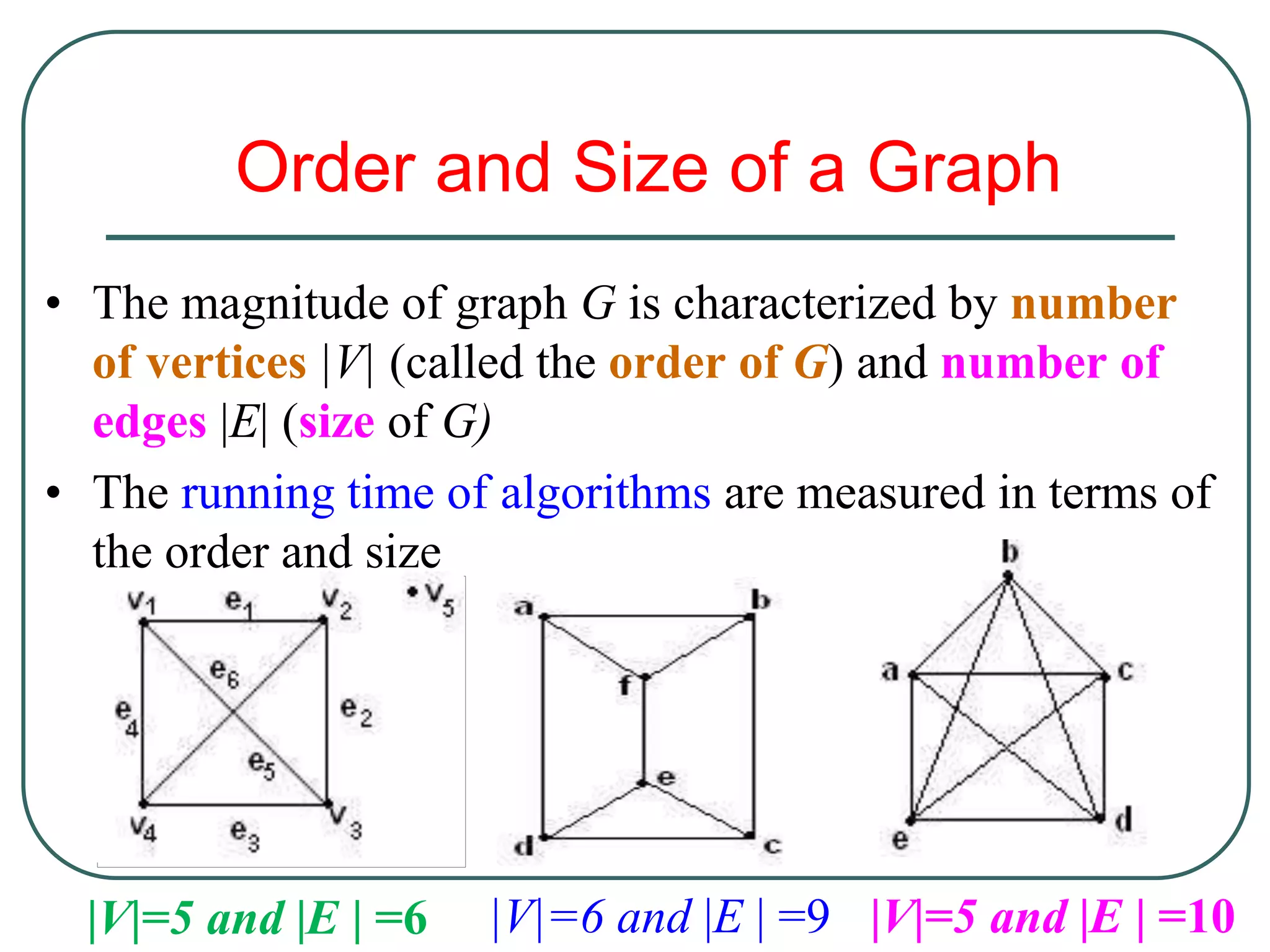
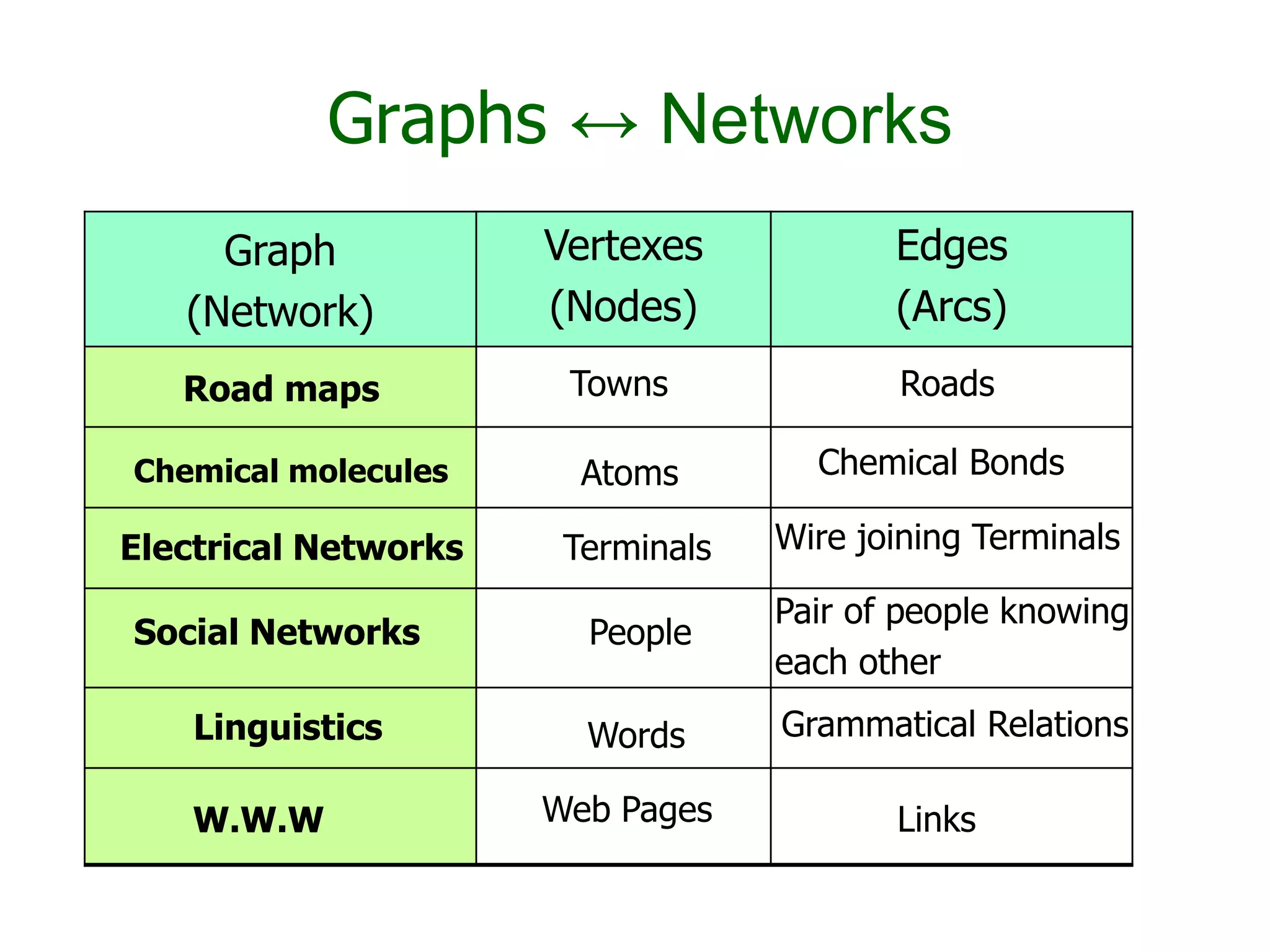
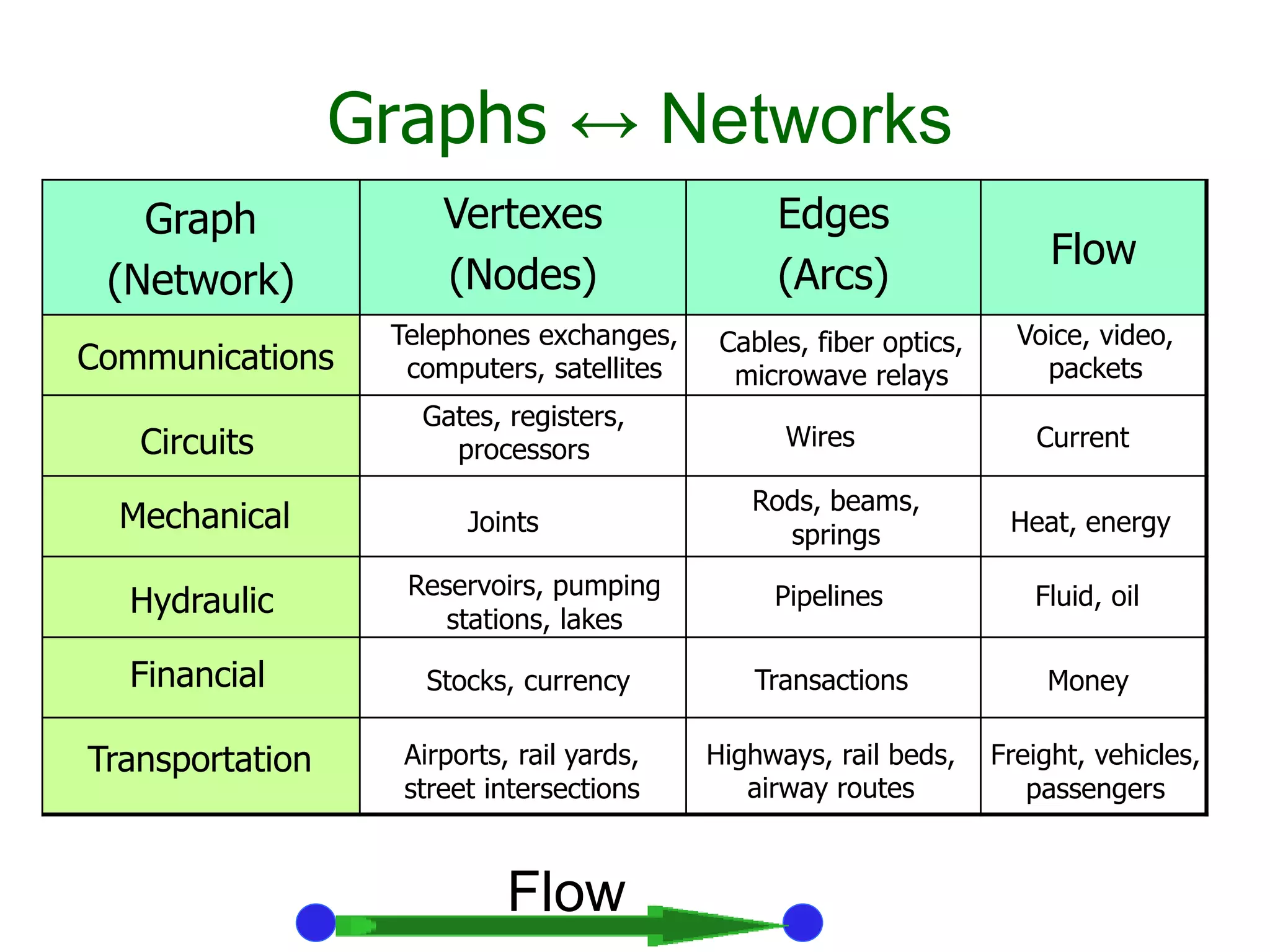
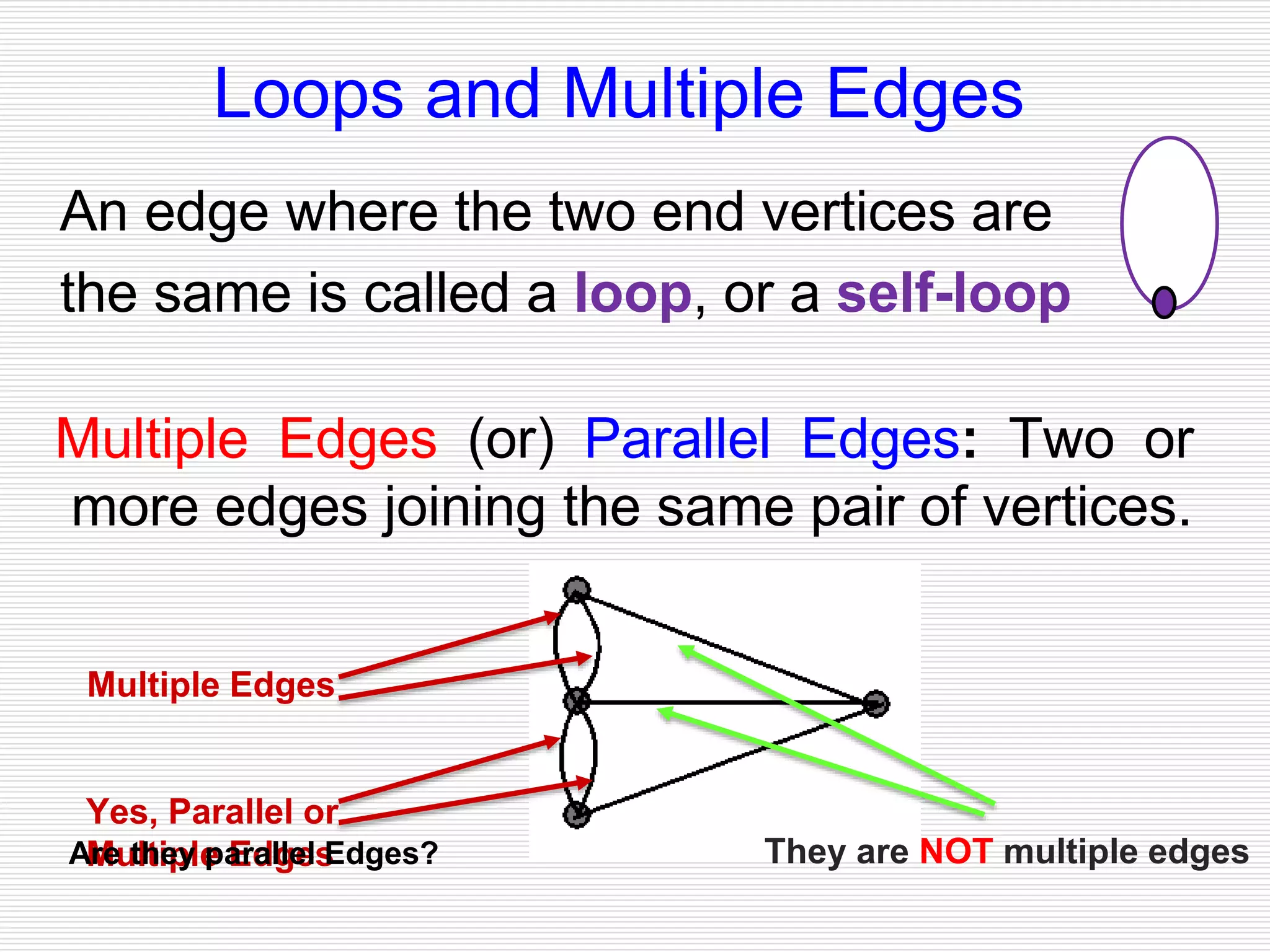
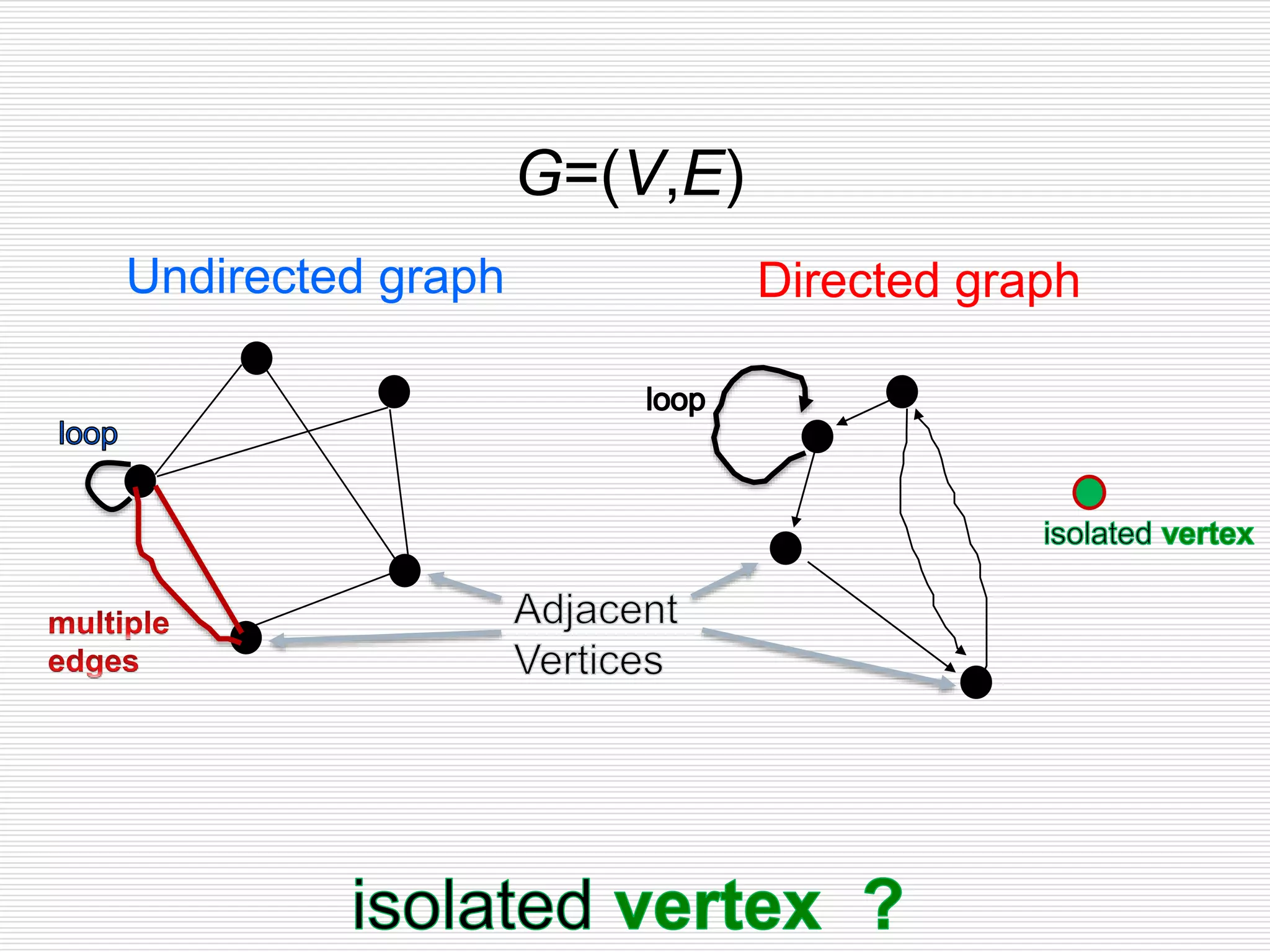
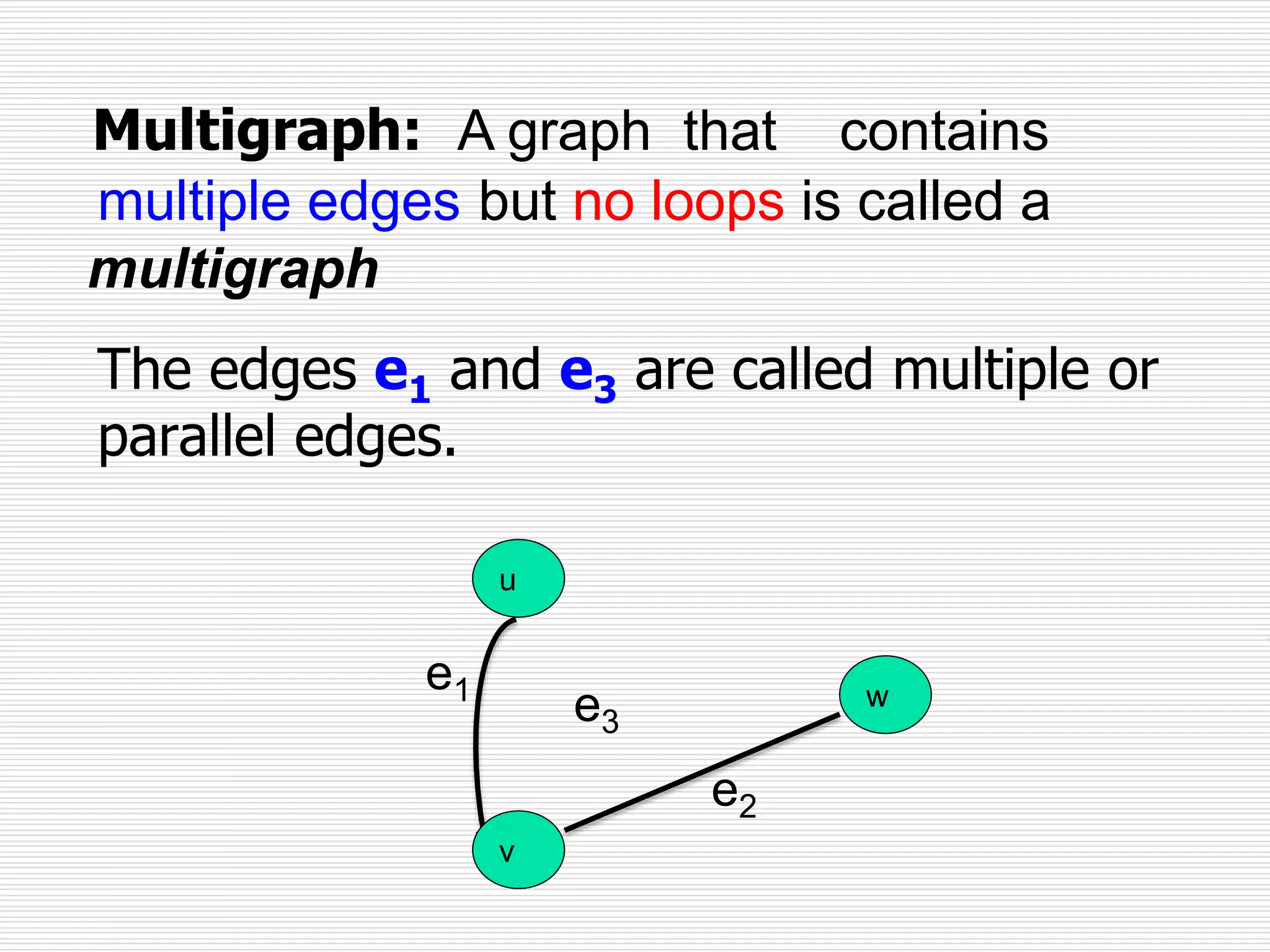
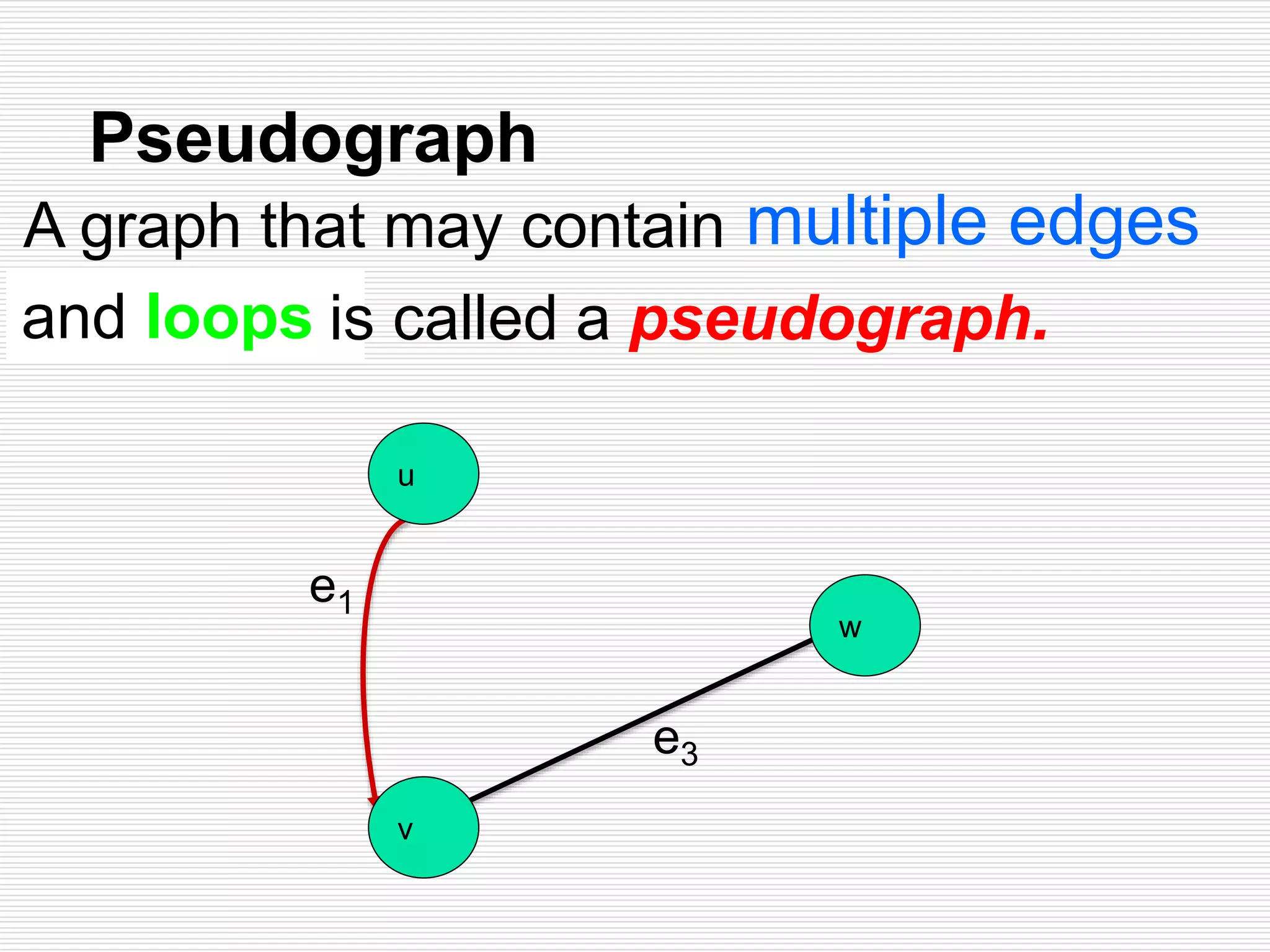
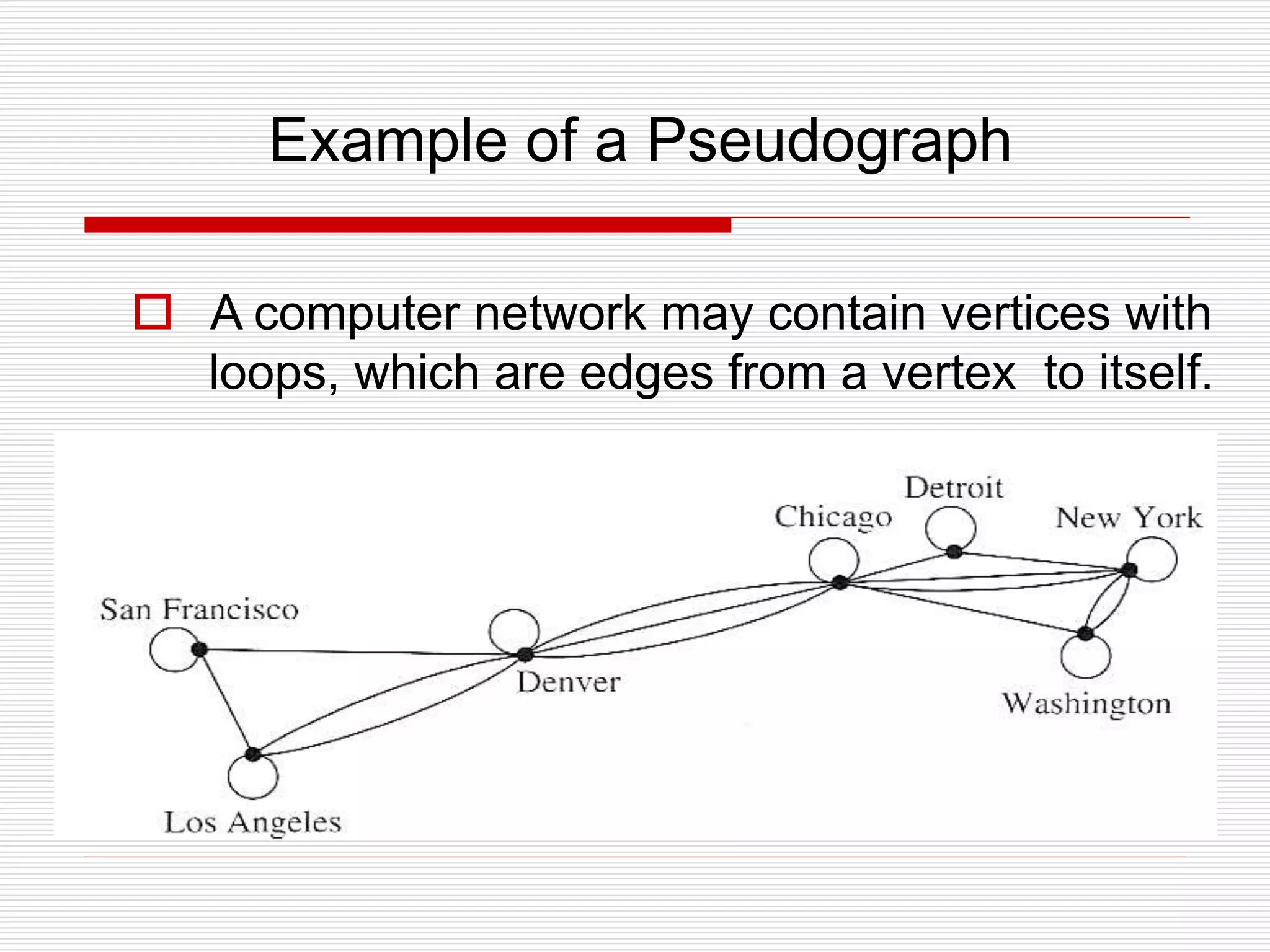
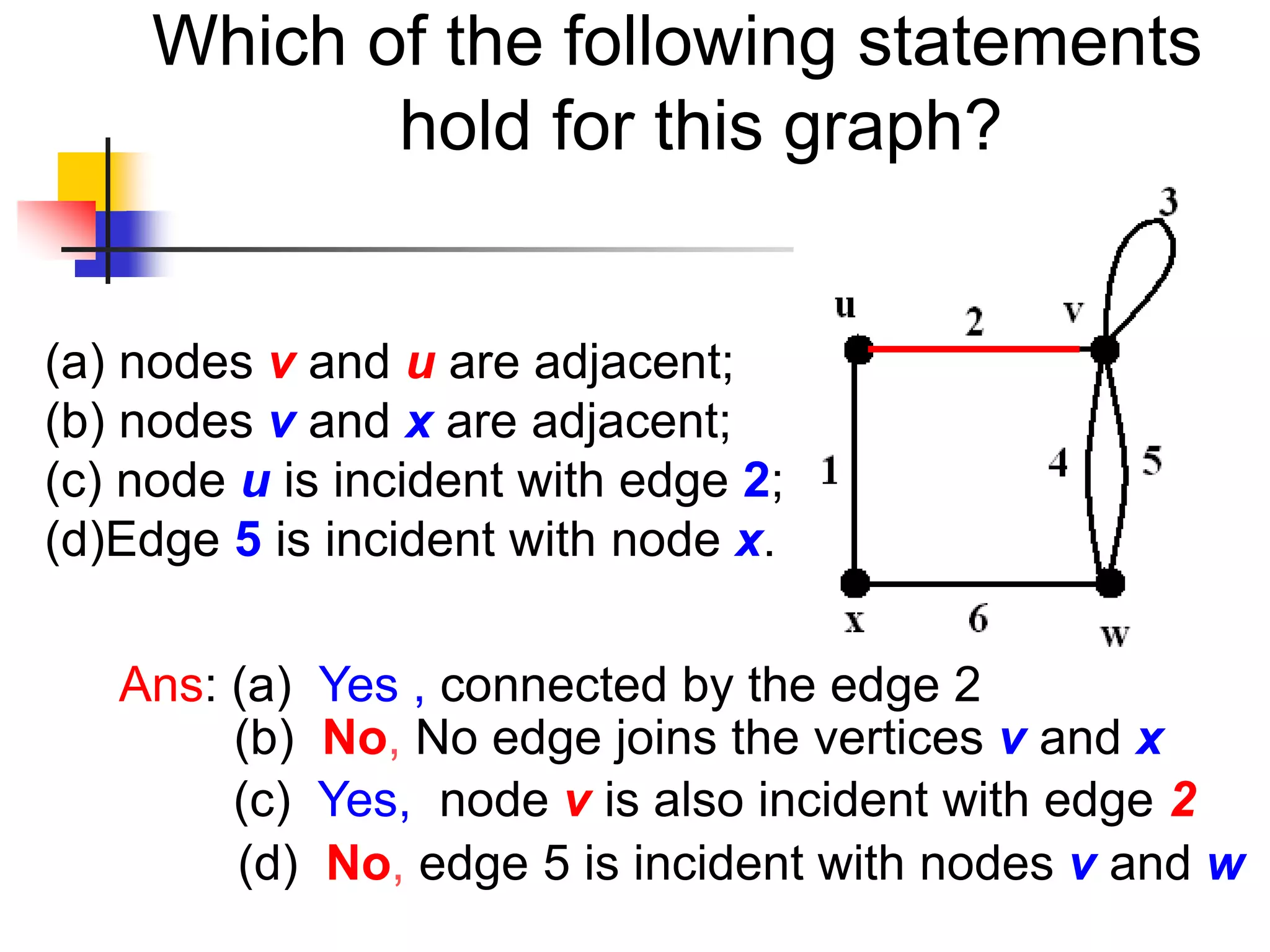
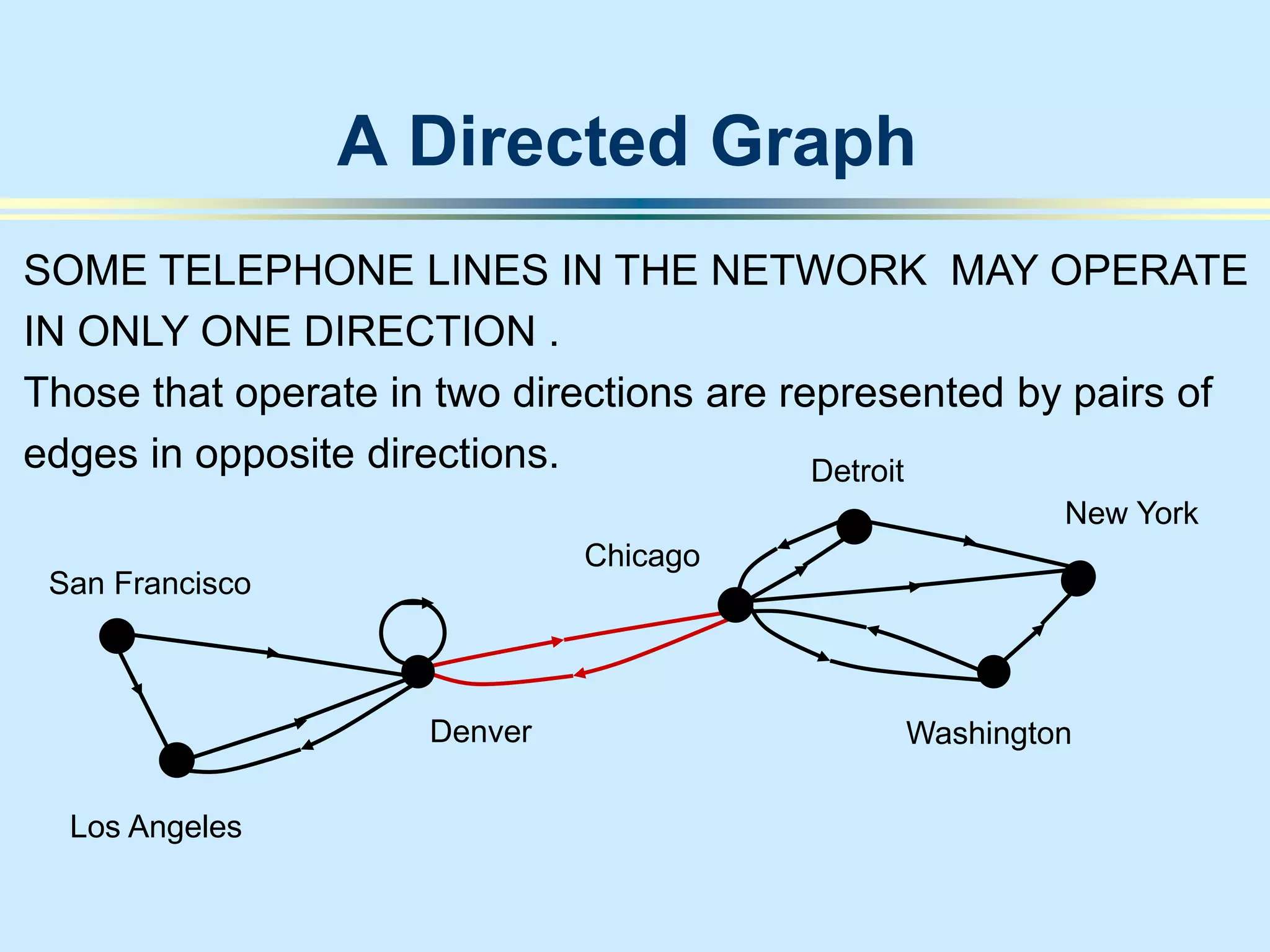
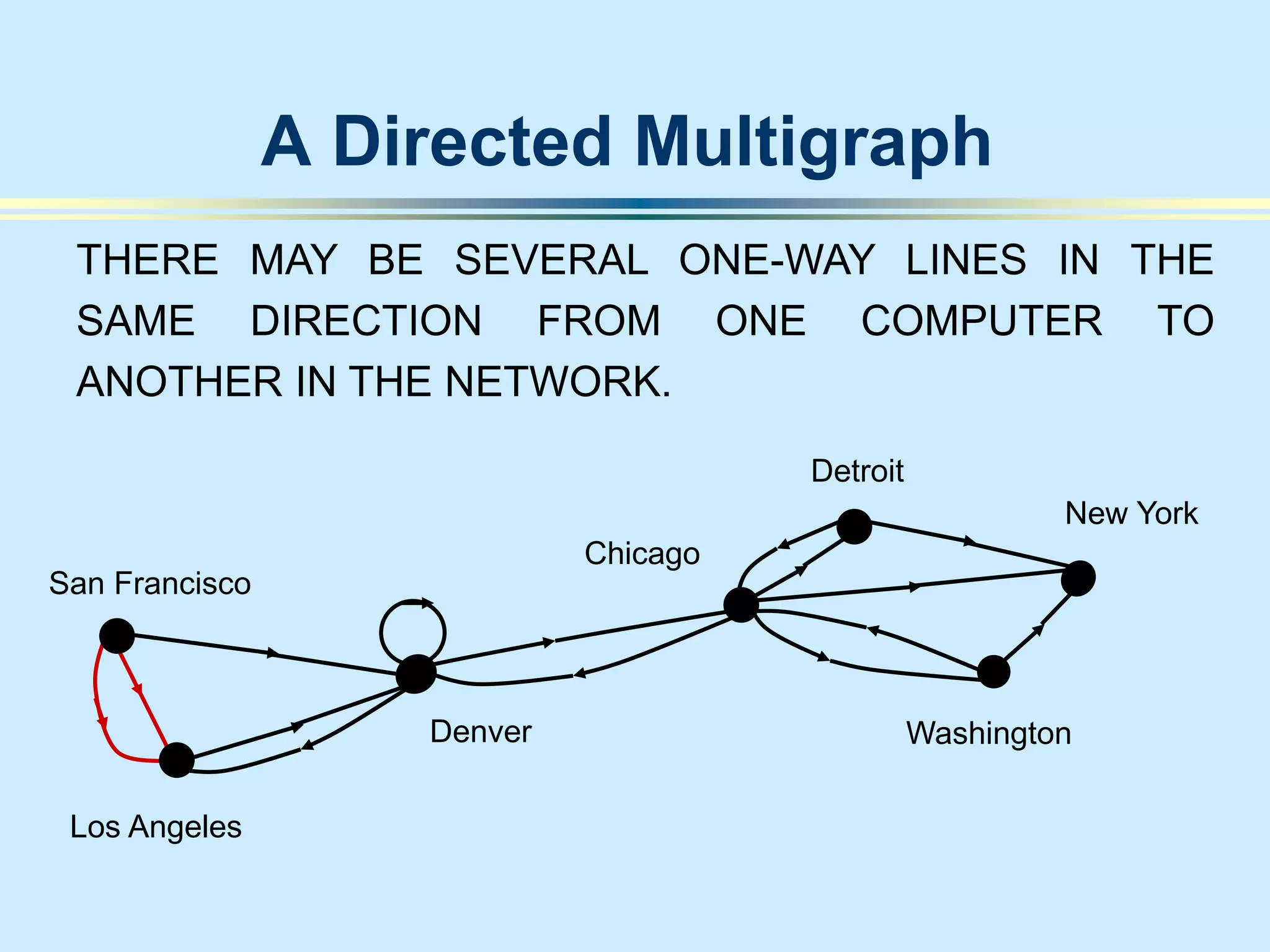
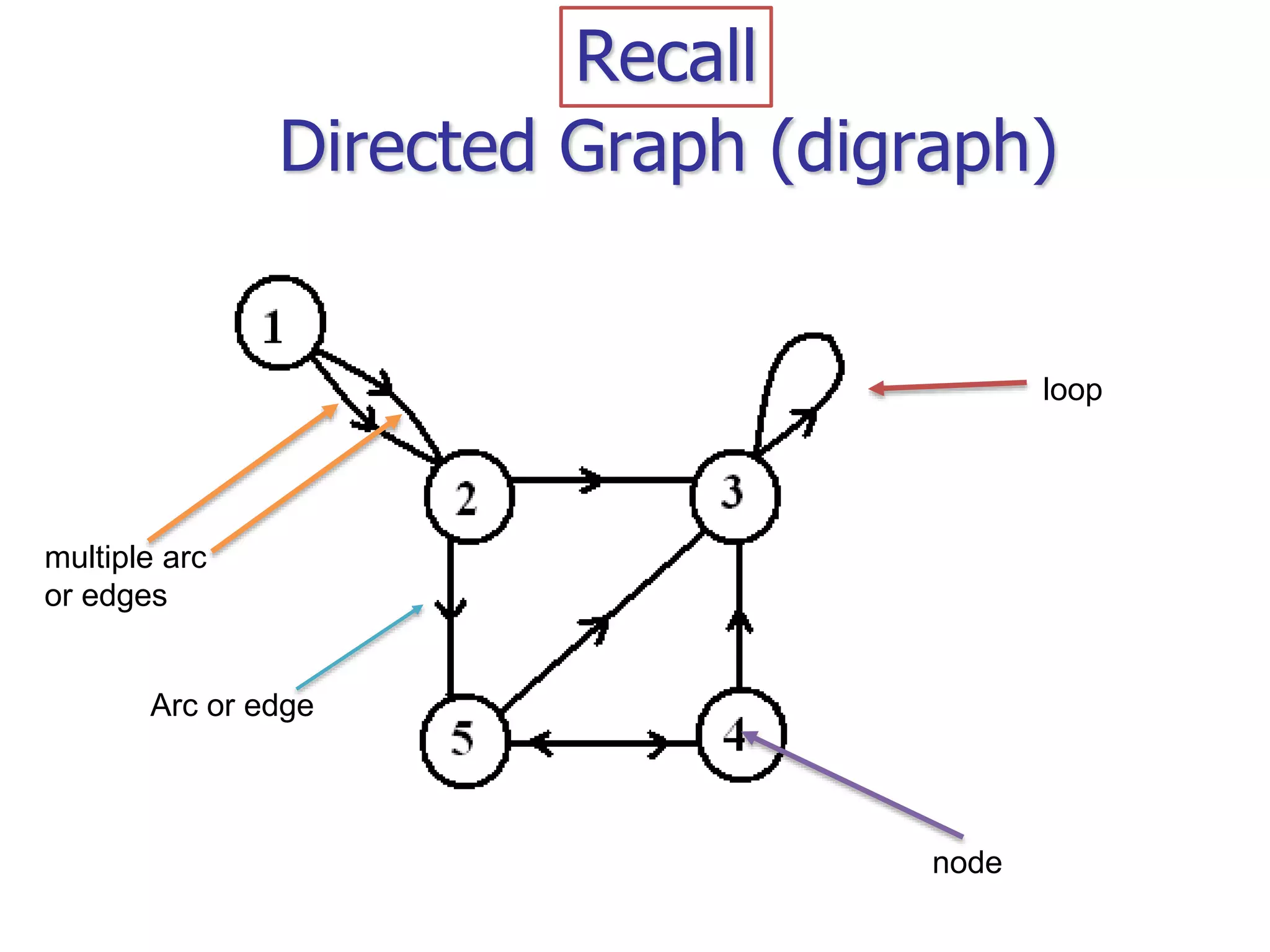
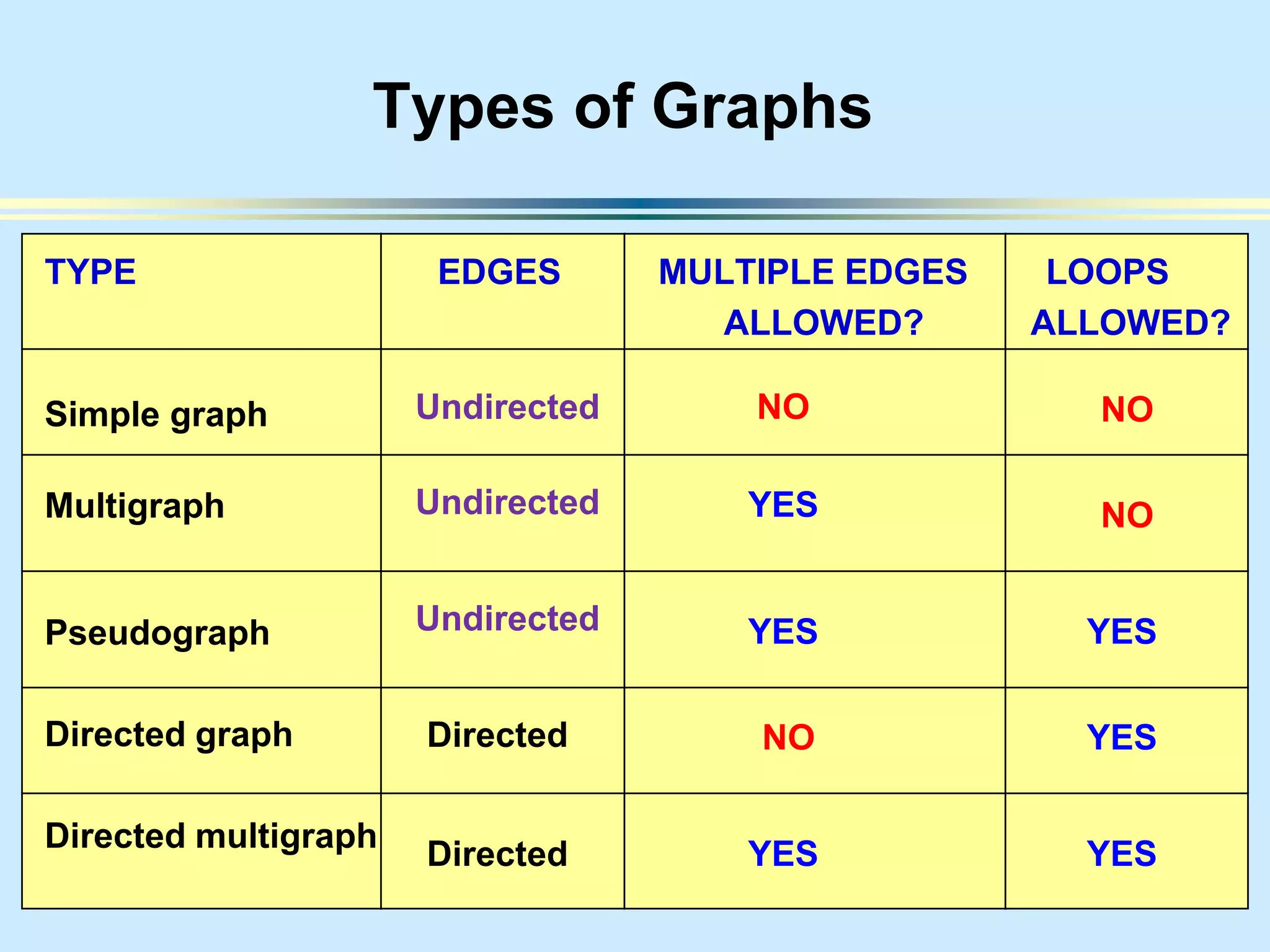
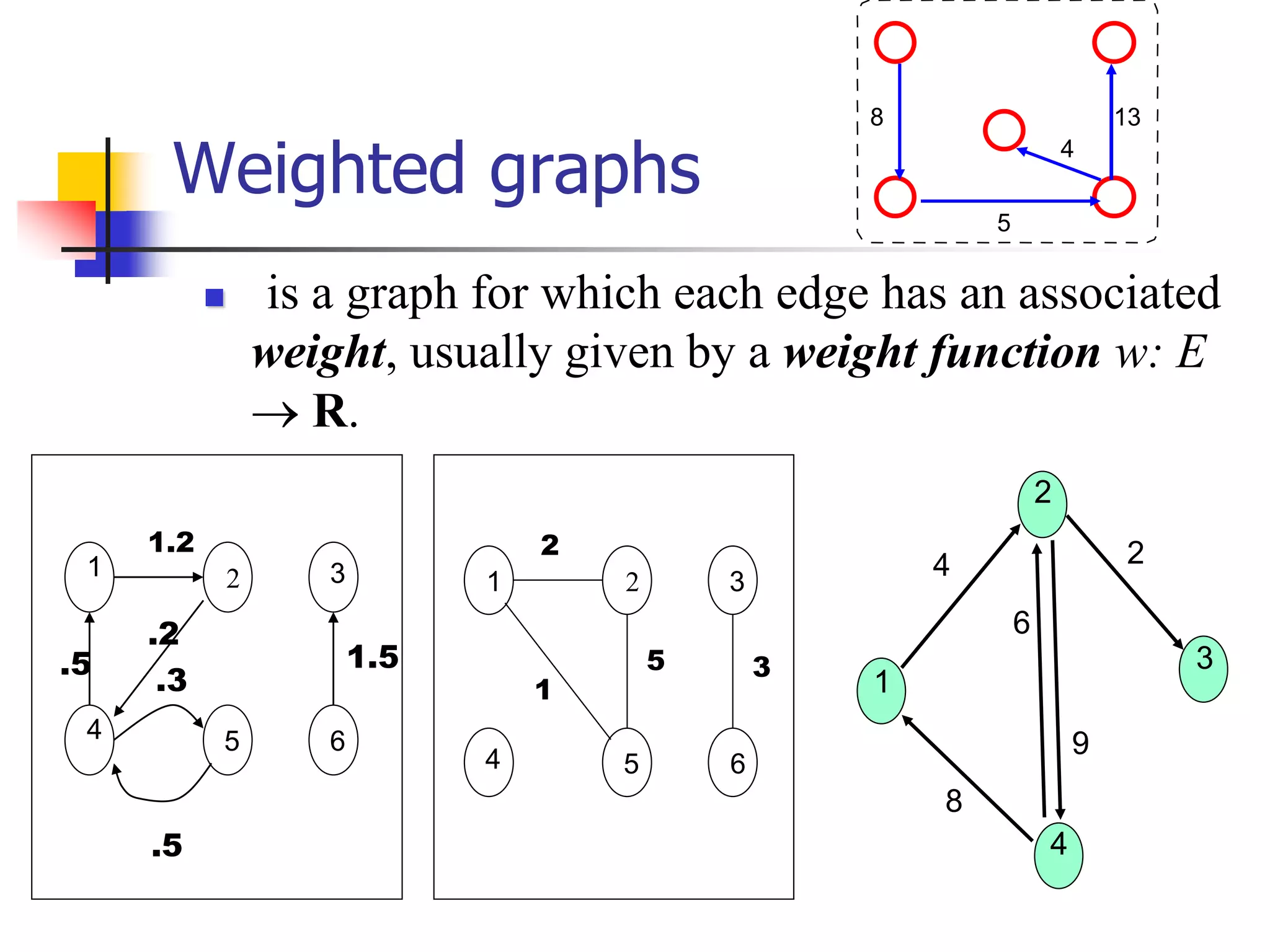
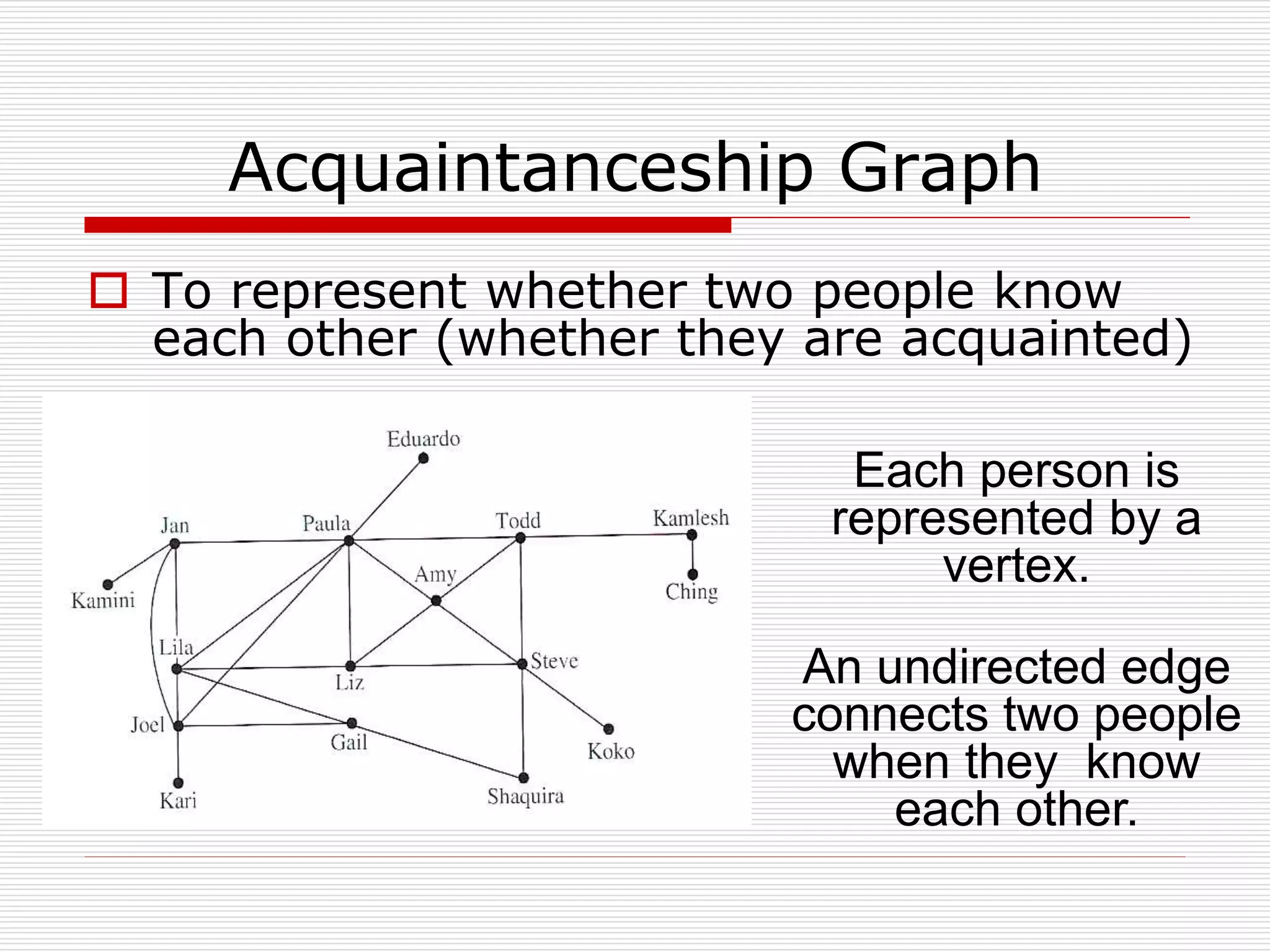
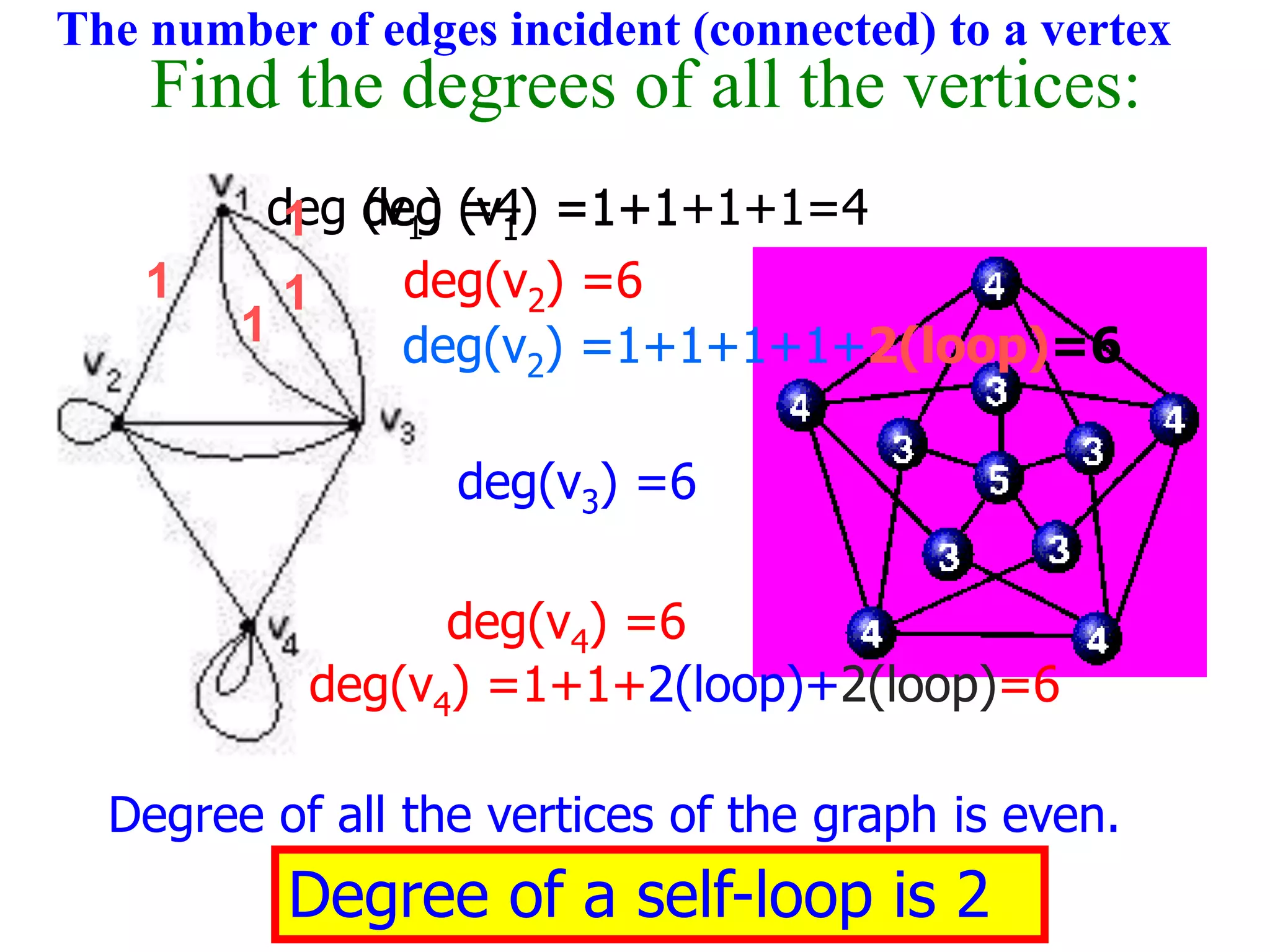
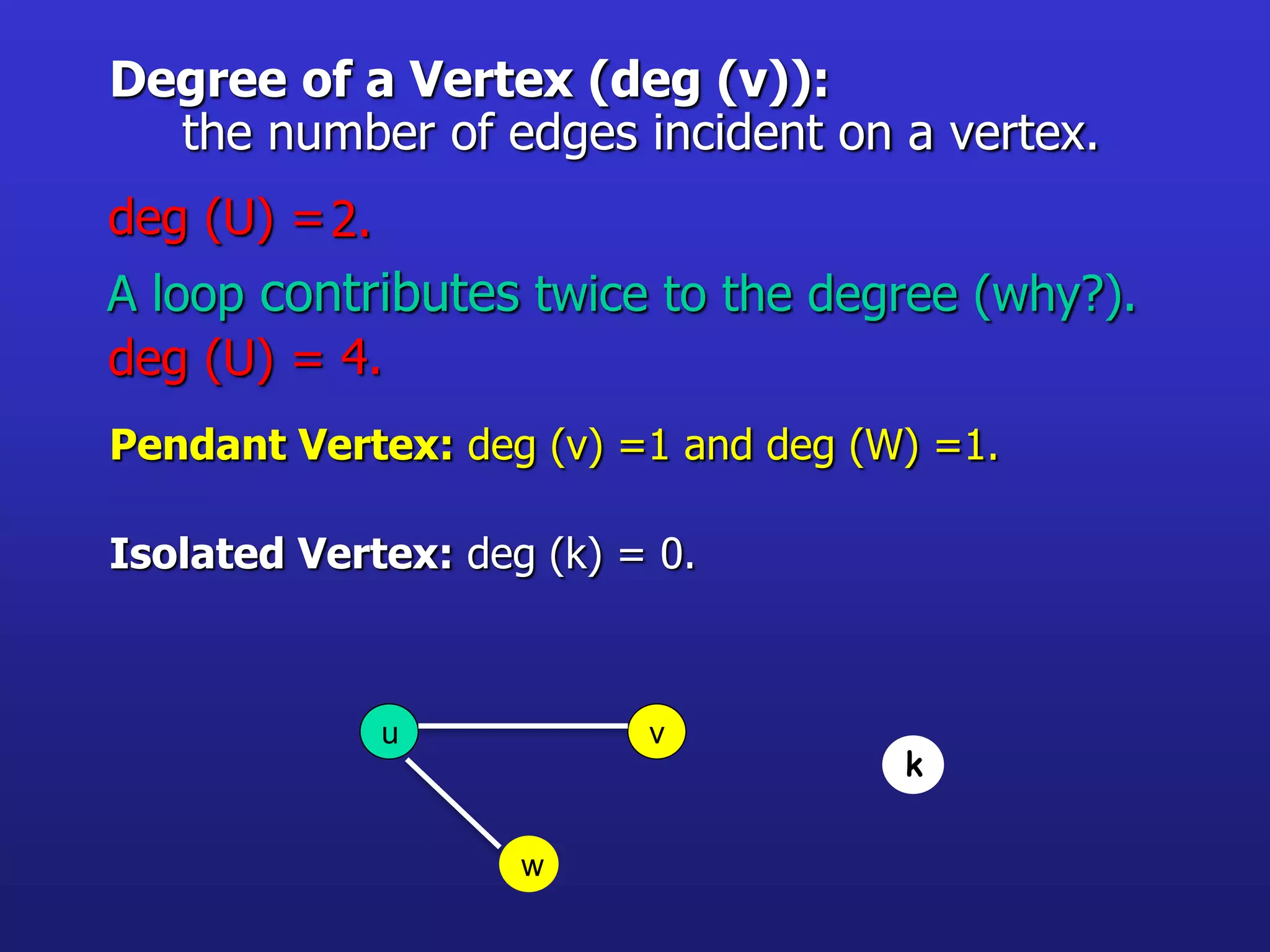
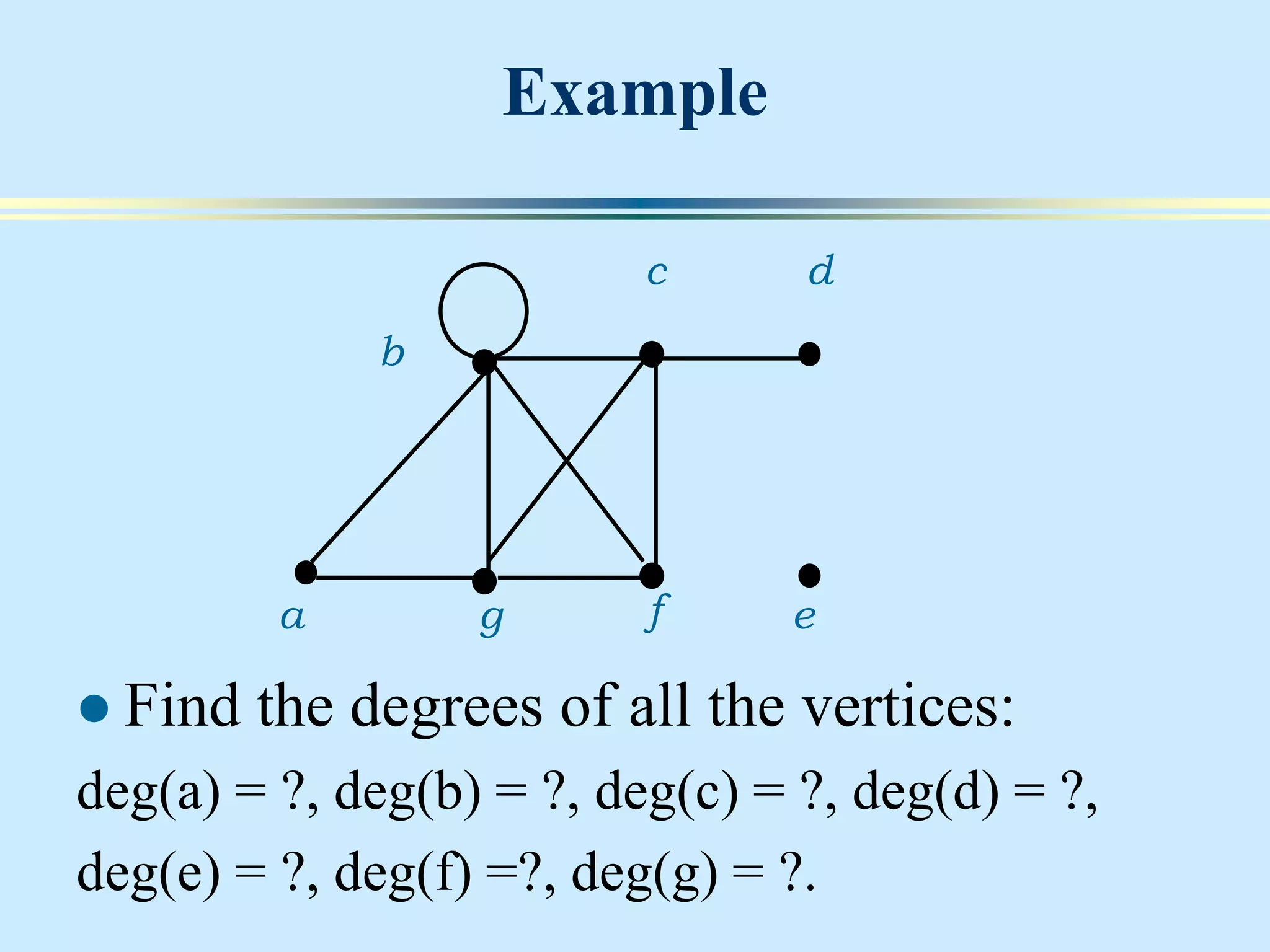
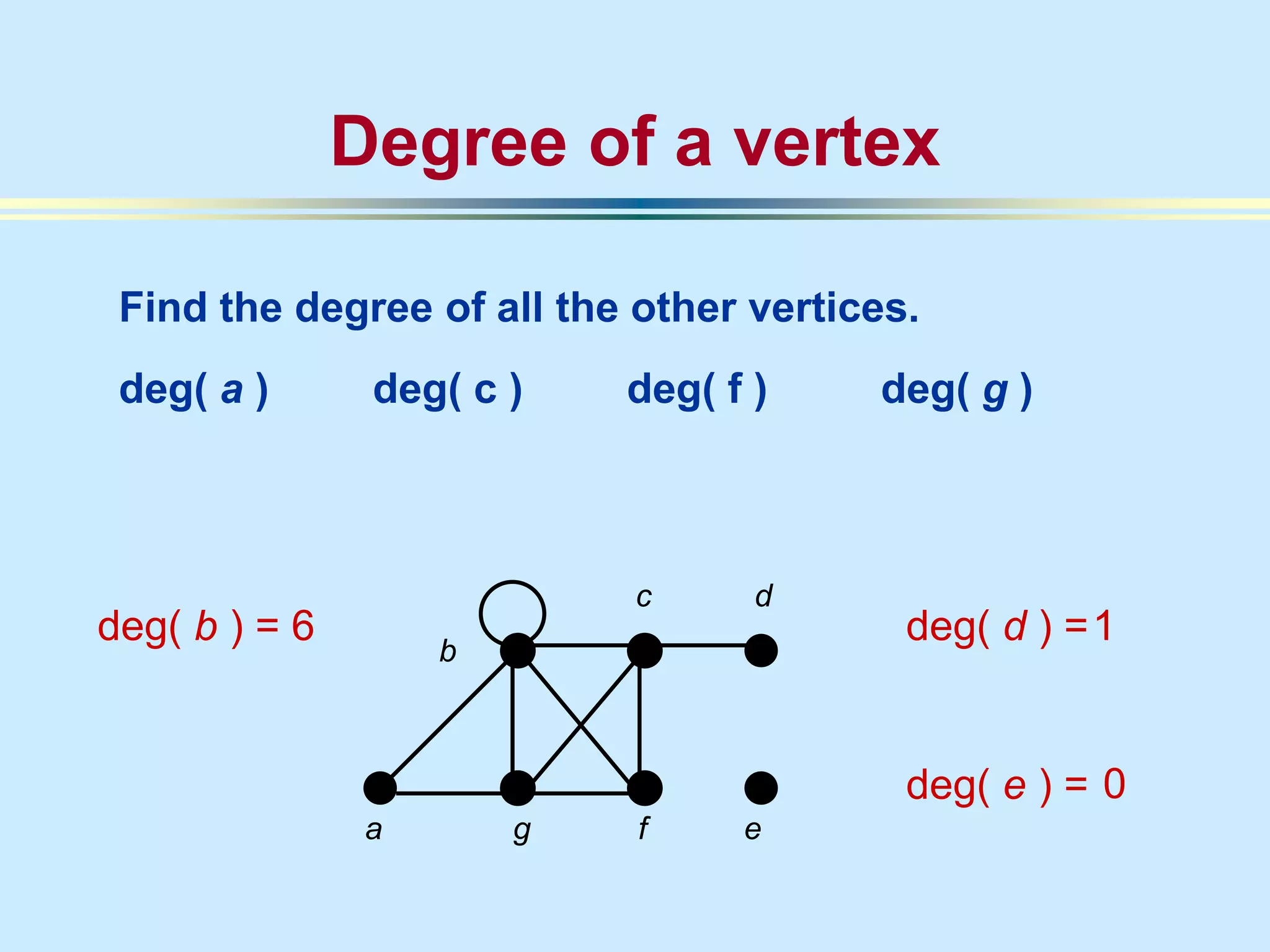
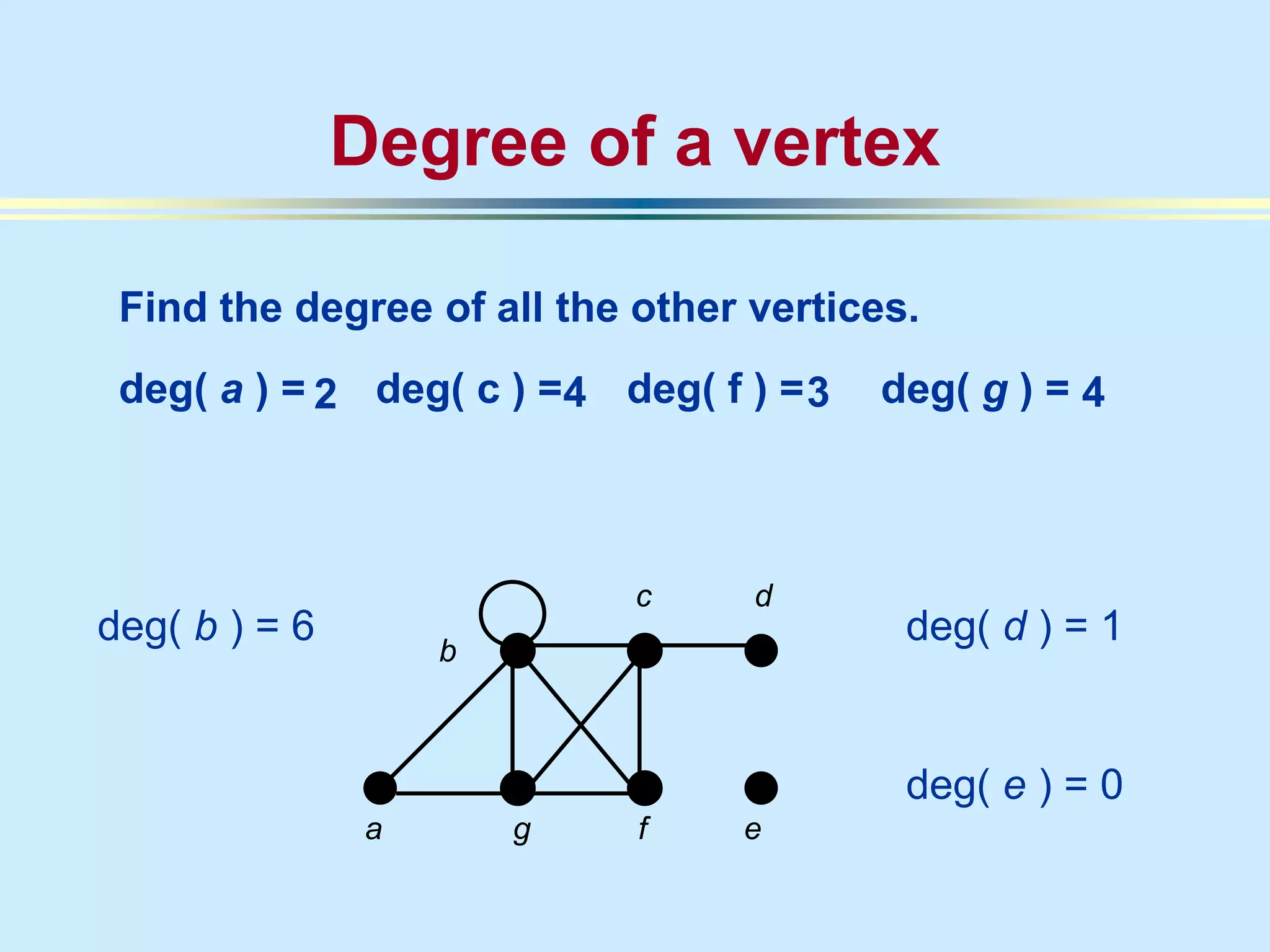
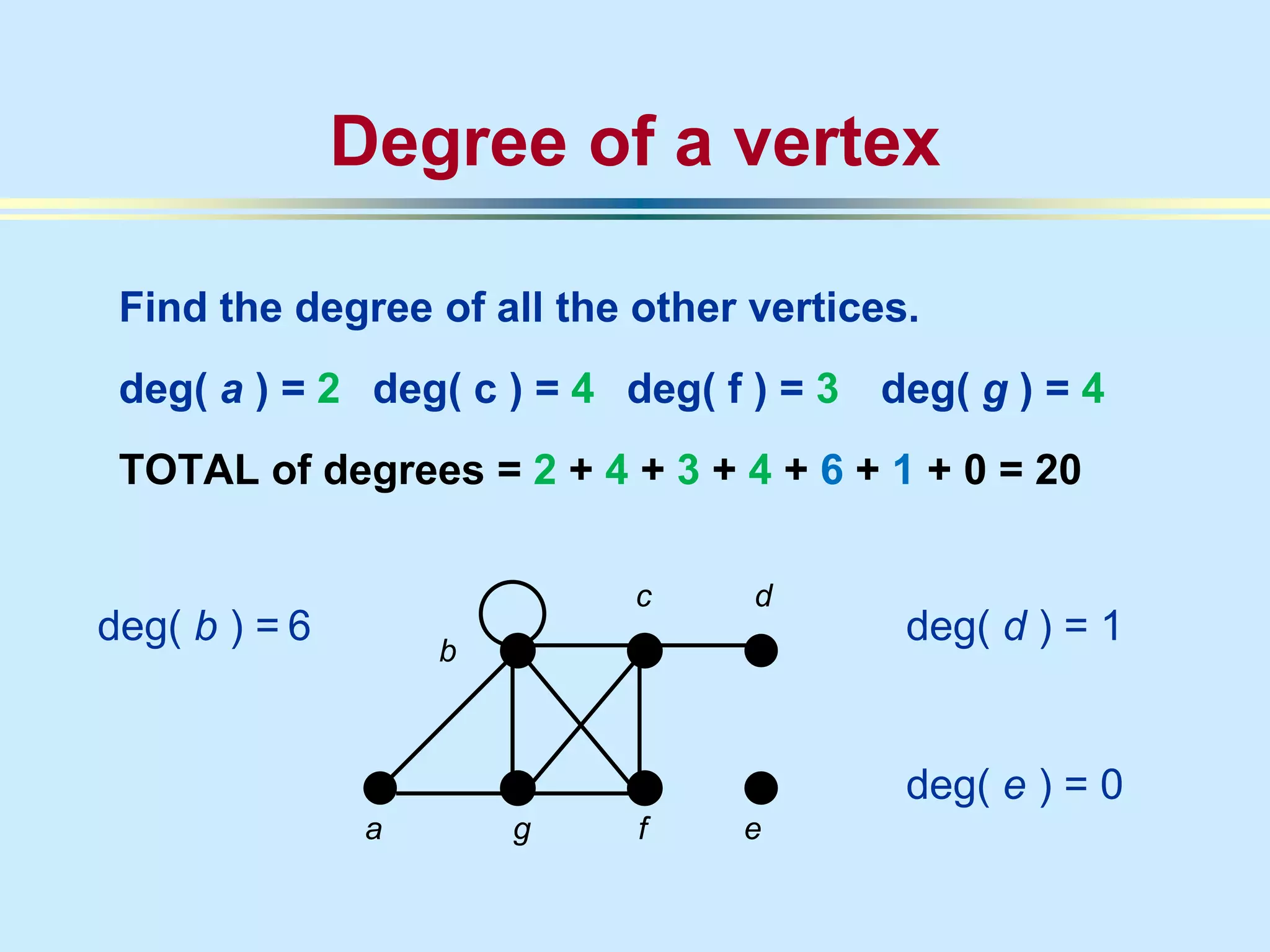
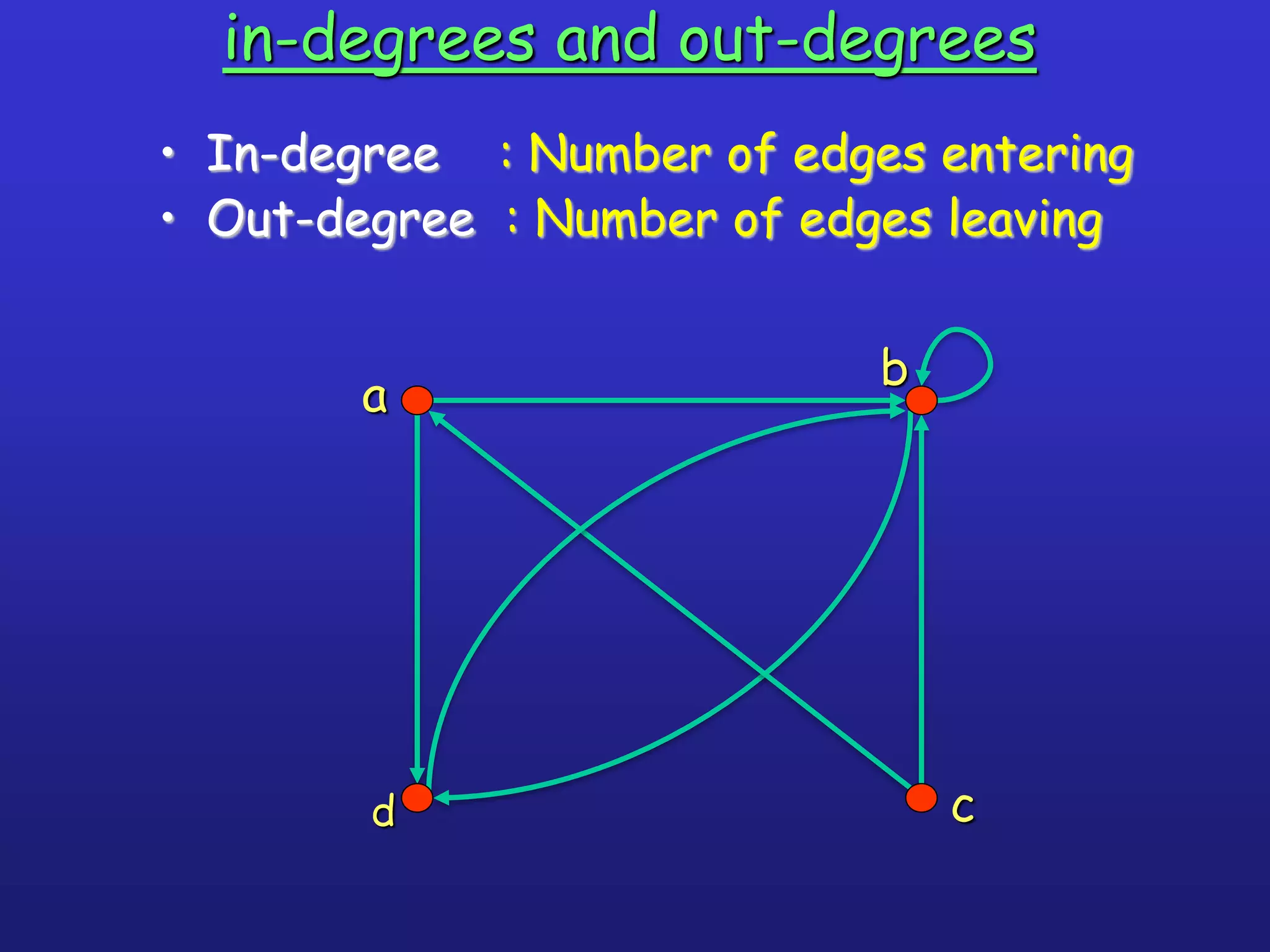
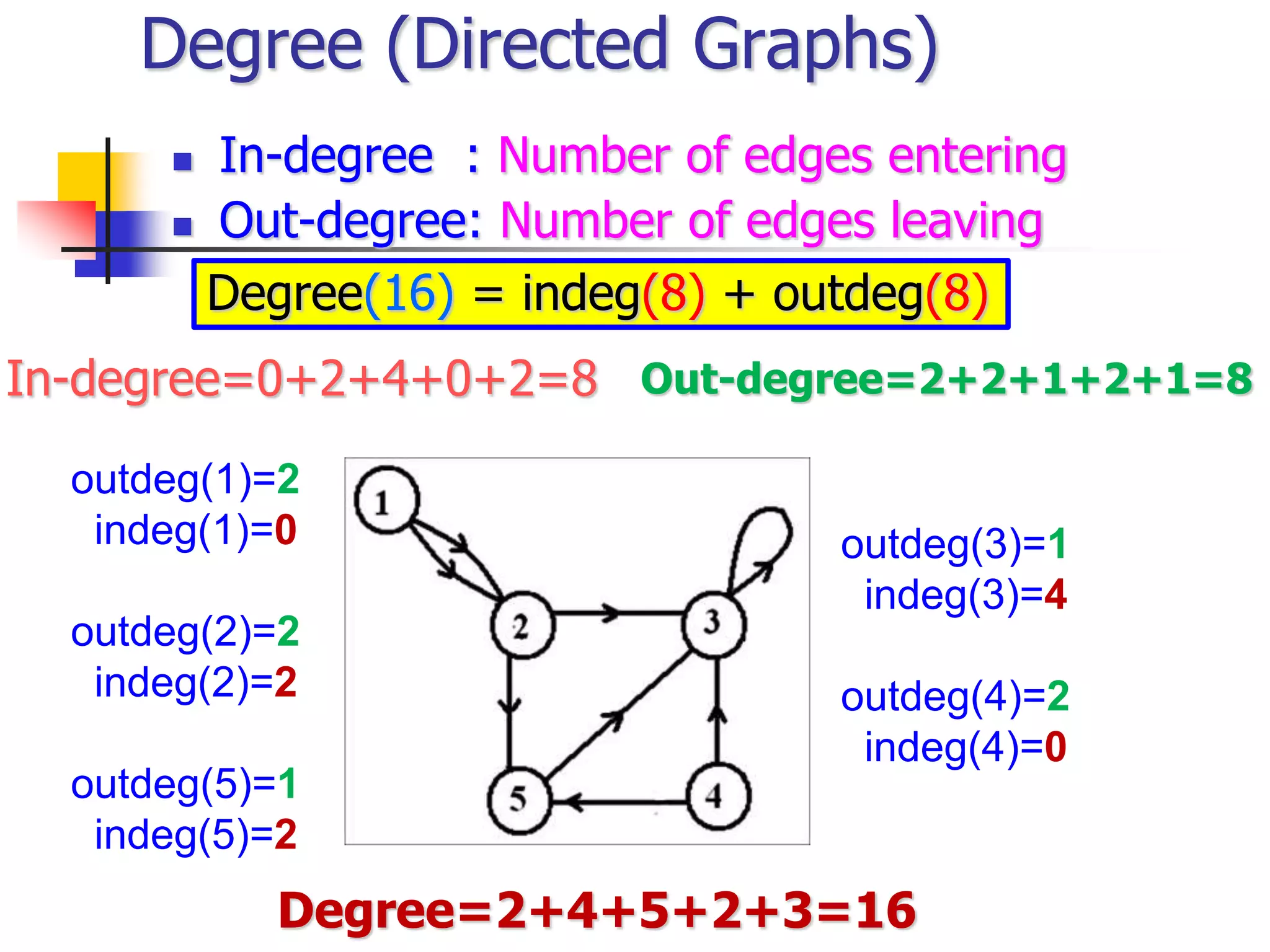
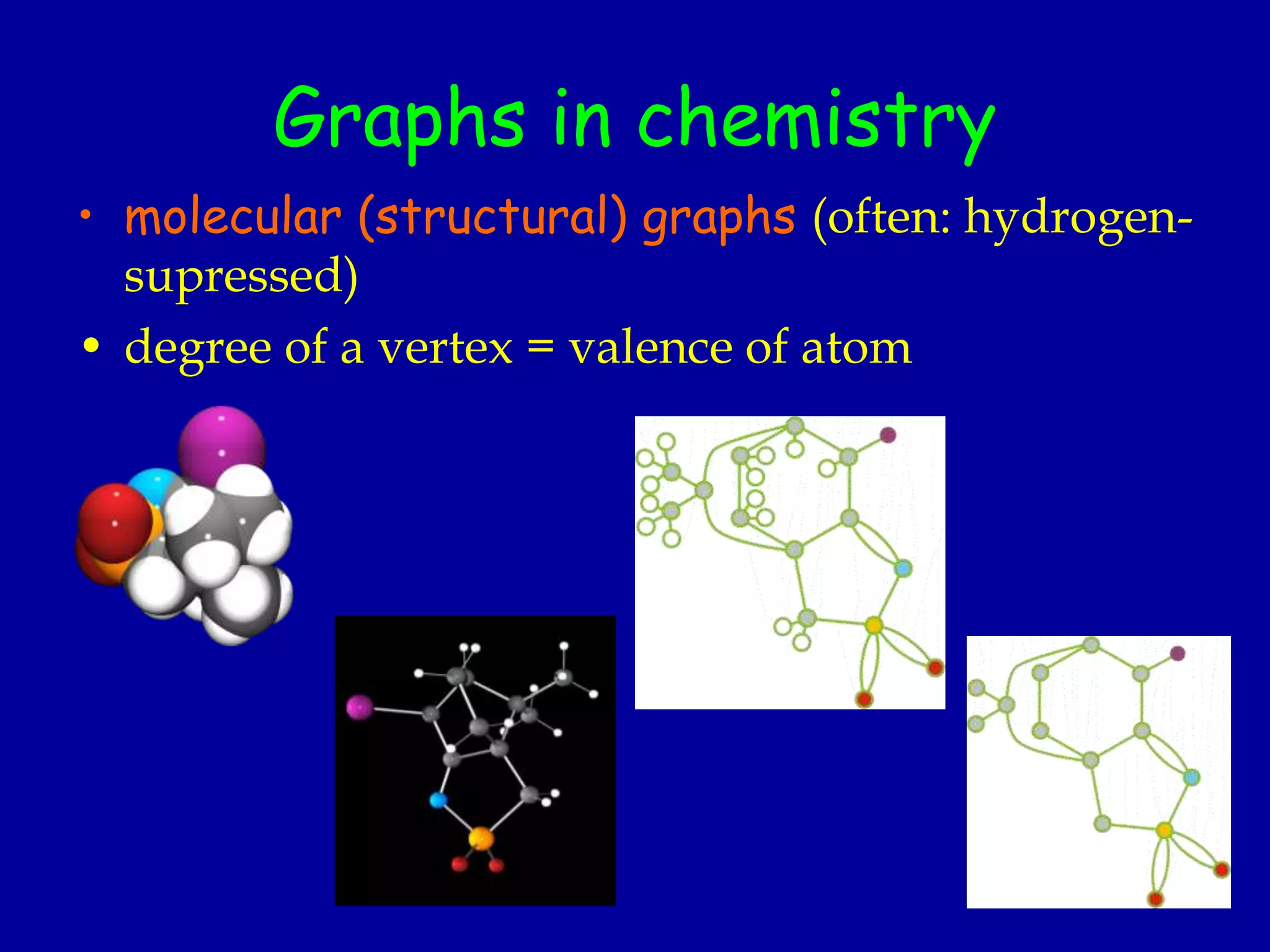
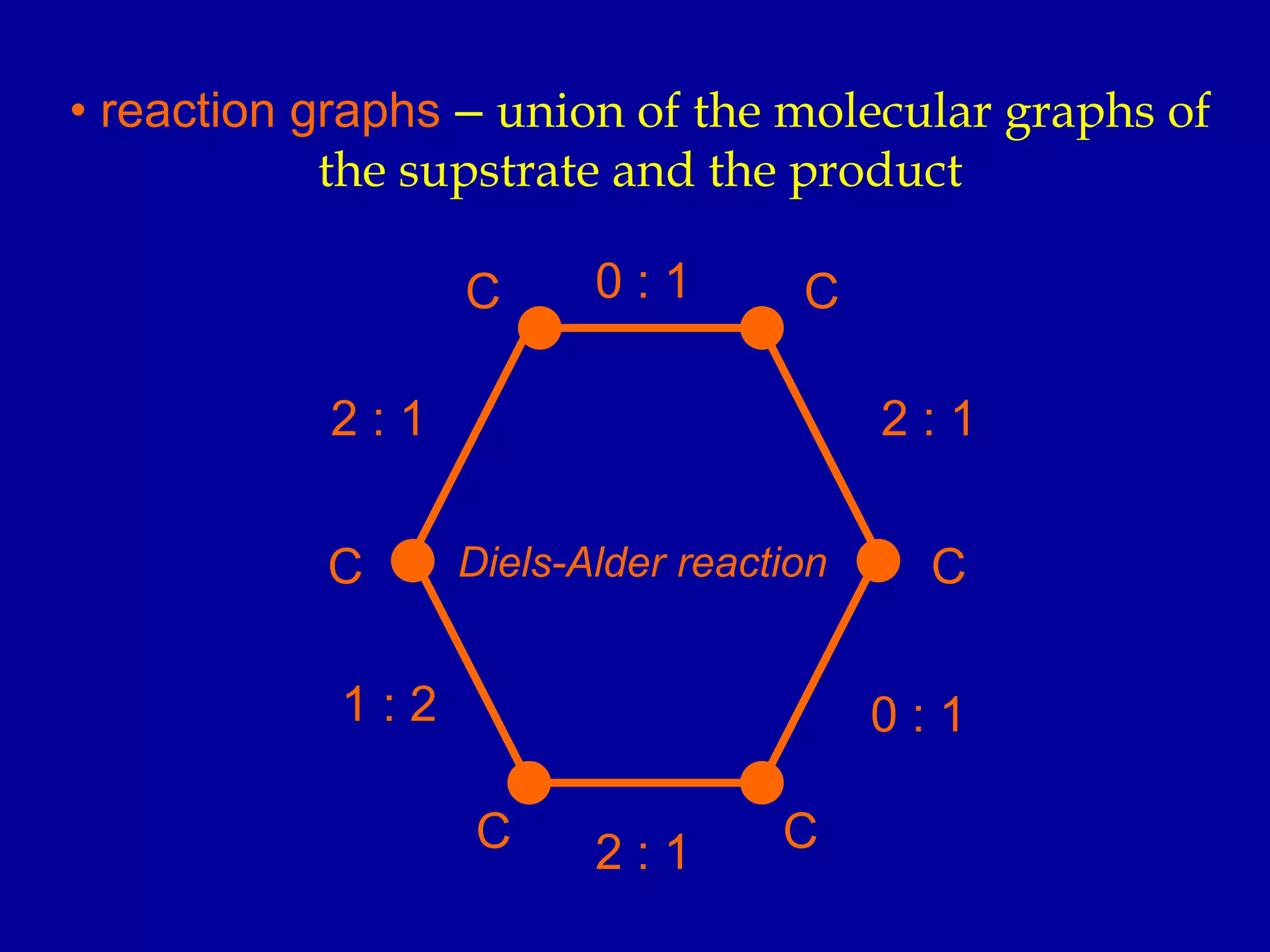
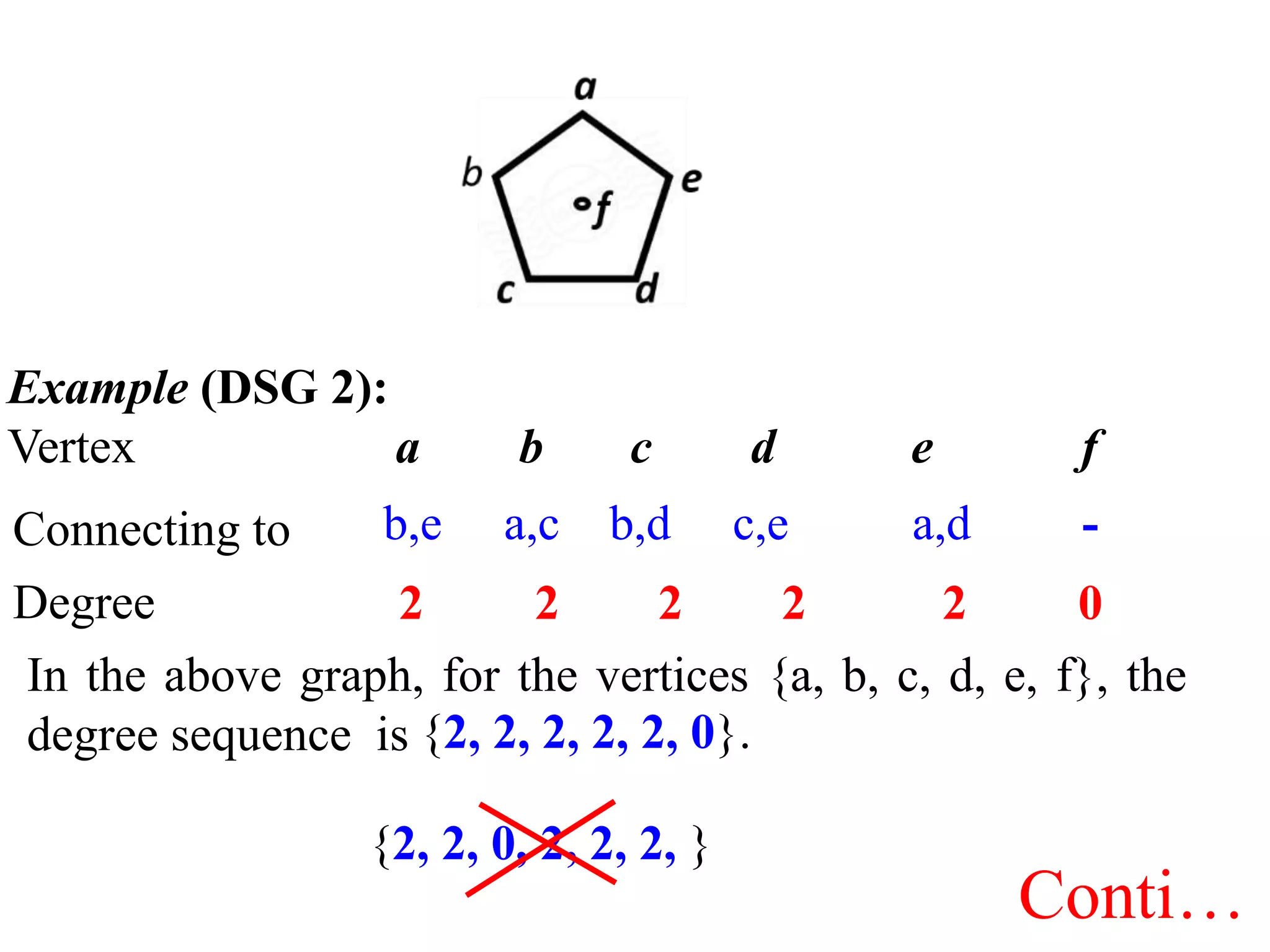
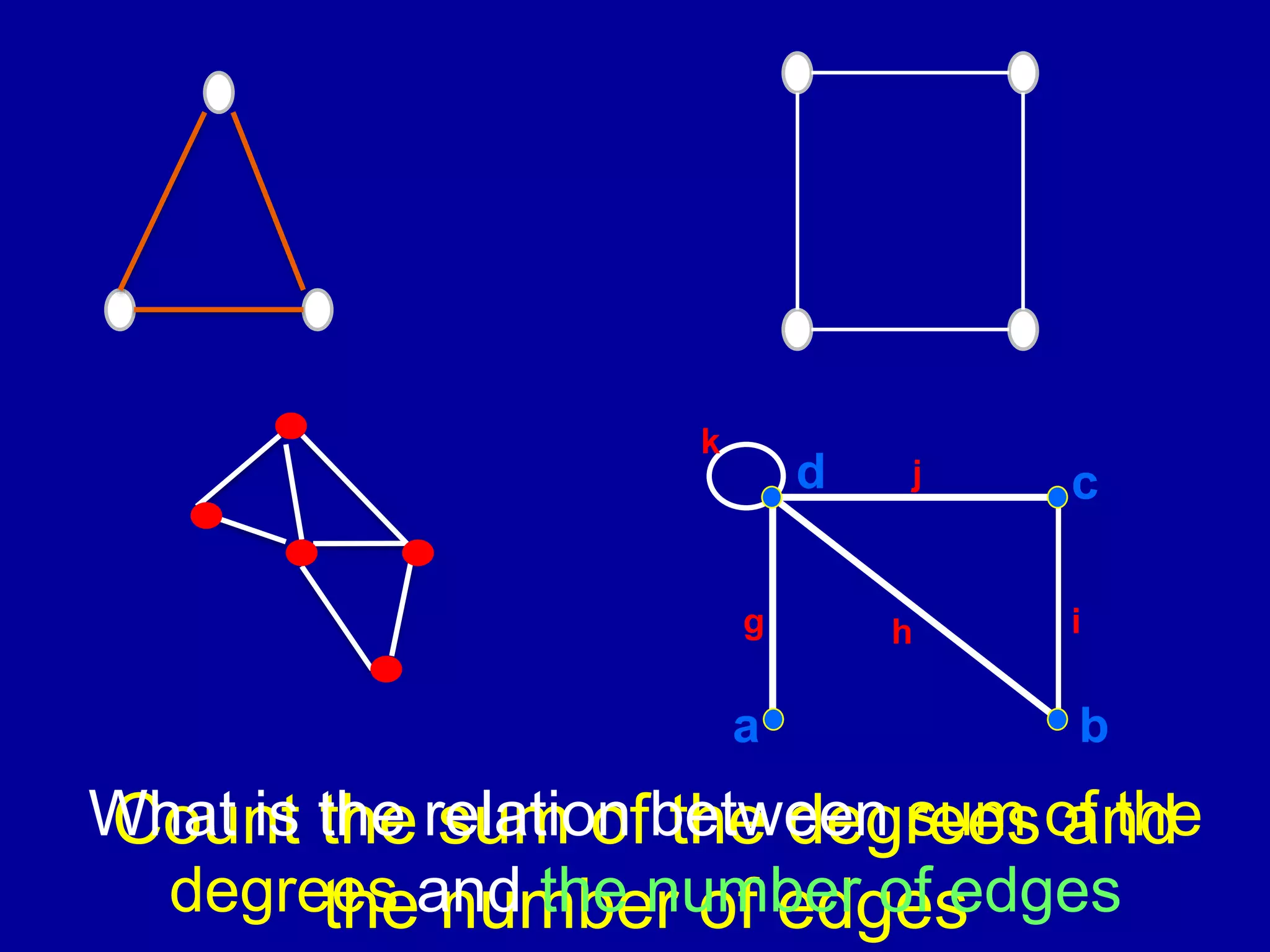
The document provides an introduction to graph theory. It lists prescribed and recommended books, outlines topics that will be covered including history, definitions, types of graphs, terminology, representation, subgraphs, connectivity, and applications. It notes that the Government of India designated June 10th as Graph Theory Day in recognition of the influence and importance of graph theory.