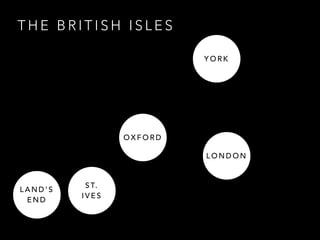
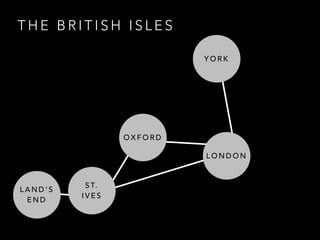
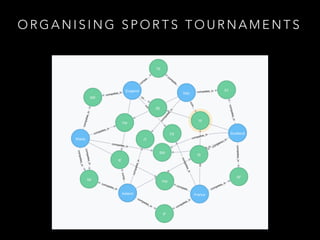
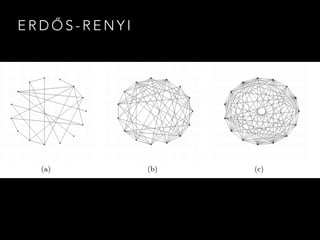
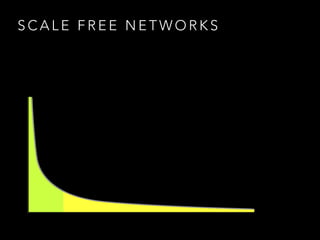
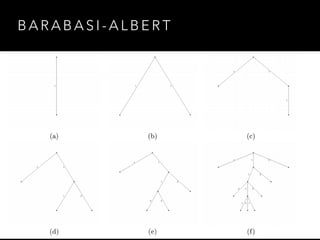
The document discusses the application of graph theory and its practical uses, particularly in data modeling and problem-solving. It highlights various concepts such as graphs, planar graphs, connectivity, spanning trees, and graph coloring, showcasing examples from real-world scenarios such as election data and sports tournament organization. The speaker emphasizes the importance of understanding graph theory to leverage data efficiently and use it in various contexts, including the internet and social networks.

1. G RA P H T H E O RY I N
P RACT I S E
D A V I D S I M O N S
@ S W A M W I T H T U R T L E S

2. W H O A M I ?
• David Simons
• @SwamWithTurtles
• github.com/
SwamWithTurtles
• Technical Lead at Softwire
and part-time hacker
• Statistician in a past life

3. T O S E E D ATA D O N E R I G H T
M Y PA S S I O N …

4. W H AT I S D ATA
D O N E R I G H T ?
• Choosing the right
database;
• Using the right
mathematical and
statistical techniques to
leverage its power

5. S Q L
• SQL has had 40 years of
academic set theory
applied to it…
• Let’s do the same with
neo4j!

6. T O D AY…
• Concepts in Graph Theory
• Theory;
• Use Cases;
• Implementation Details
• Reward: What shape is
the internet?

7. W H AT I S A G R A P H ?
G R A P H T H E O RY

8. W H AT I S A G R A P H ?
Taken from Jim Webber’s Dr. Who Dataset

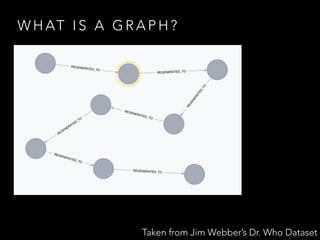
9. W H AT I S A G R A P H ?
{ (V, E) : V = [n], E ⊆ V(2) }

10. W H AT I S A G R A P H ?
{ (V, E) : V = [n], E ⊆ V(2) }
Made up of two parts,
“V” and “E”

11. W H AT I S A G R A P H ?
{ (V, E) : V = [n], E ⊆ V(2) }
V is a set of n items

12. W H AT I S A G R A P H ?
Vertex Set

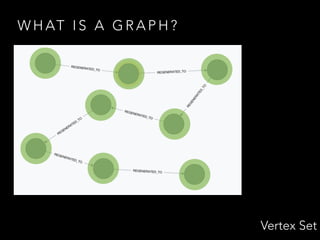
13. W H AT I S A G R A P H ?
{ (V, E) : V = [n], E ⊆ V(2) }
E is made up of pairs
of elements of V
(Ordered and
not necessarily distinct)

14. W H AT I S A G R A P H ?
Edge Set

15. G I V I N G R E A L
W O R L D
M E A N I N G S T O V
A N D E
W H A T I S G R A P H I C A L
M O D E L L I N G ?

16. B R I D G E S AT K Ö N I G S B E R G

17. B R I D G E S AT K Ö N I G S B E R G
V =
bits of land
E =
bridges

18. E L E C T I O N D ATA

19. E L E C T I O N D ATA

20. E L E C T I O N D ATA
E =
(e.g.) member of, held in,
stood in…
V =
elections, constituencies,
years, politicians and parties

21. W H E R E D O E S
N E O 4 J F I T I N ?
• Stores both the vertex set
and the edge set as first
class objects:
• Queryable
• Can store properties
• “Typed”

22. W H Y L E A R N
T H E T H E O RY ?
• Tells us what we can do
• Let’s us utilise many years
of academics
• Gives us a common
language

23. C A S E S T U D Y
T H E B R E A K D O W N …

24. T H E B R I T I S H
I S L E S
A G R A P H O F

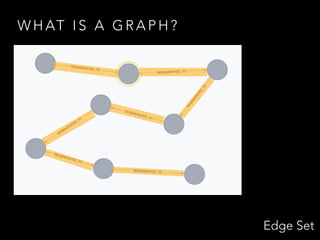
25. W H AT I S A G R A P H ?
{ (V, E) : V = [n], E ⊆ V(2) }

26. W H AT I S A G R A P H ?
{ (V, E) :
V = Places of Interest,
E = Places that are connected}

27. T H E B R I T I S H I S L E S
L O N D O N
L A N D ’ S
E N D
O X F O R D
Y O R K
S T.
I V E S

28. T H E B R I T I S H I S L E S
L O N D O N
L A N D ’ S
E N D
O X F O R D
Y O R K
S T.
I V E S

29. P L A N A R I T Y
• A planar graph is one that
can be drawn on paper
with its edges crossing
• There are easy theories
that tell you when a graph
is planar
• Used for planning
construction of roads

30. C O N N E C T I V I T Y
• A graph is connected if
there is a path between
any two points
• A graph is k-connected if
you need to remove at
least k vertices to stop it
being connected
• Used for infrastructure
robustness studies

31. S PA N N I N G
T R E E
• A tree is a graph with no
loops
• A spanning tree is a
graph with tree with every
vertex connected
• Ensure resources flow
through a network

32. C O L O U R I N G
G R A P H T H E O RY

33. W E L I K E T H E
S I M P L E T H I N G S
I N L I F E
M A T H E M A T I C I A N S …

34. C O L O U R I N G
I N …
M A T H E M A T I C I A N S …

35. C O L O U R I N G
I N …
• Take your graph (V, E)
• Vertex Colouring
• Assign every vertex a
colour such that no two
adjacent vertices have
the same colour.

36. T H AT ’ S A L L V E RY
W E L L …

37. O R G A N I S I N G
S P O R T S
T O U R N A M E N T S
W H Y ?

38. O R G A N I S I N G
S P O R T S
T O U R N A M E N T S
• Graph Model
• V = all matches that
must be played
• E = a team is the same
across two matches
• Two vertices the same
colour => they can be
played simultaneously

39. O R G A N I S I N G S P O R T S T O U R N A M E N T S

40. O R G A N I S I N G S P O R T S T O U R N A M E N T S

41. O T H E R
U S E S …
• Mobile Phone Tower
frequency assignment
• V = mobile phone
towers
• E = towers so close
their waves will
interfere
• Colours = frequencies

42. O T H E R
U S E S …
• Solving SuDokus
• V = Squares on a
SuDoku grid
• E = Knowledge that
they must be different
numbers
• Colours = numbers 1
to 9

43. O T H E R U S E S …
http://watch.neo4j.org/video/74870401
Avoiding Deadlocks in Neo4j on Z-Platform

44. N O J AVA F R A M E W O R K …
Y E T !

45. R A N D O M G R A P H S
G R A P H T H E O RY

46. R A N D O M N E S S
S E E M S C A RY…
B U T WA I T…

47. R A N D O M N E S S
S E E M S C A RY…
• It can be!
• Someone should do a
talk about that…
• https://
www.youtube.com/
watch?v=rV9dqR0P0lQ

48. A graph with a fixed number of vertices, whose
edges are generated non-deterministically

49. U S E C A S E S
R A N D O M G R A P H S S T I L L H A V E …

50. S T U B B E D T E S T
D ATA
U S E C A S E S

51. S T U B B E D
T E S T D ATA
• Suppose you have a
method that coloured the
vertices of a graph…
• How could you test that?

52. S T U B B E D
T E S T D ATA
S T U B B E D D ATA S E T
A P P LY M E T H O D
A S S E RT T H AT:
* E V E RY N O D E H A S A
C O L O U R
* N O T W O A D J A C E N T
N O D E S S H A R E A
C O L O U R

53. S T U B B E D
T E S T D ATA
R A N D O M LY
G E N E R AT E D D ATA S E T
A P P LY M E T H O D
A S S E RT T H AT:
* E V E RY N O D E H A S A
C O L O U R
* N O T W O A D J A C E N T
N O D E S S H A R E A
C O L O U R

54. S I M U L AT I O N
A L G O R I T H M S
U S E C A S E S

55. - N A S D A Q . C O M
“solving a problem by performing a large number
of trail runs… and inferring a solution from the
collective results of the trial runs.”

56. W H Y
S I M U L AT I O N ?
• Modelling underlying
randomness
• Underlying question is
impossible (or hard) to
solve
• Trying to model something
of which we cannot have
full knowledge

57. A N D …
• It’s possible to use
randomness and always be
correct
• cf. ‘Probabilistic
Combinatorics’ by Paul
Erdős

58. H O W C A N W E
A C C O M P L I S H I T I N N E O 4 J ?

59. D I Y
I N T H E O RY …

60. D I Y

61. G R A P H A W A R E
I N P R A C T I S E …

62. G R A P H A W A R E
• “#1 Neo4j Consultancy”
• Open-sourced a lot of
projects under GPL3
including:
• TimeTree
• Reco
• Algorithms

63. G R A P H A W A R E

64. G R A P H A W A R E

65. A graph with a fixed number of vertices, whose
edges are generated non-deterministically

66. E R D Ő S - R E N Y I
• Take a graph with n vertices;
• For each pair of vertices, randomly connect them with
probability p

67. E R D Ő S - R E N Y I

68. I WA N T T O M O D E L
D ATA A B O U T
K E V I N B A C O N
B U T …

69. I WA N T T O M O D E L
D ATA A B O U T
S P R E A D O F H I V
B U T …

70. I WA N T T O M O D E L
D ATA A B O U T
S C A L E F R E E
N E T W O R K S
B U T …

71. S C A L E F R E E
N E T W O R K S
• As the system grows, we
have:
• A small number of
highly connected
hubs
• A large number of
sparsely connected
nodes

72. S C A L E F R E E N E T W O R K S
H U B S S PA R S E N O D E S
A C T O R
C O W O R K E R S
Blockbuster stars,
like Kevin Bacon
Drama college graduate
#1828, #1829, #1830…
S P R E A D O F
H I V
Patriarchs
Less privileged society
members
C H E M I C A L
R E A C T I O N S
Catalysts Inert Chemicals

73. S C A L E F R E E N E T W O R K S

74. B A R A B A S I - A L B E R T
• Take a graph with 2 (connected) vertices
• Add vertices one at a time such that it is more likely to
add vertices to a node that is already connected
• Repeat until you have n vertices

75. B A R A B A S I - A L B E R T

76. Y O U R R E WA R D
R E M E M B E R …

77. I WA N T T O M O D E L
D ATA A B O U T
T H E I N T E R N E T
B U T …

78. O V E R V I E W
• Looking at graph theory
can give us a common
language
• Utilising techniques means
we don’t have to solve
problems from scratch each
time (e.g. colouring,
simulation)
• The internet looks like
Kevin Bacon’s career

79. A N Y Q U E ST I O N S ?
@ S W A M W I T H T U R T L E S
S W A M W I T H T U R T L E S . C O M