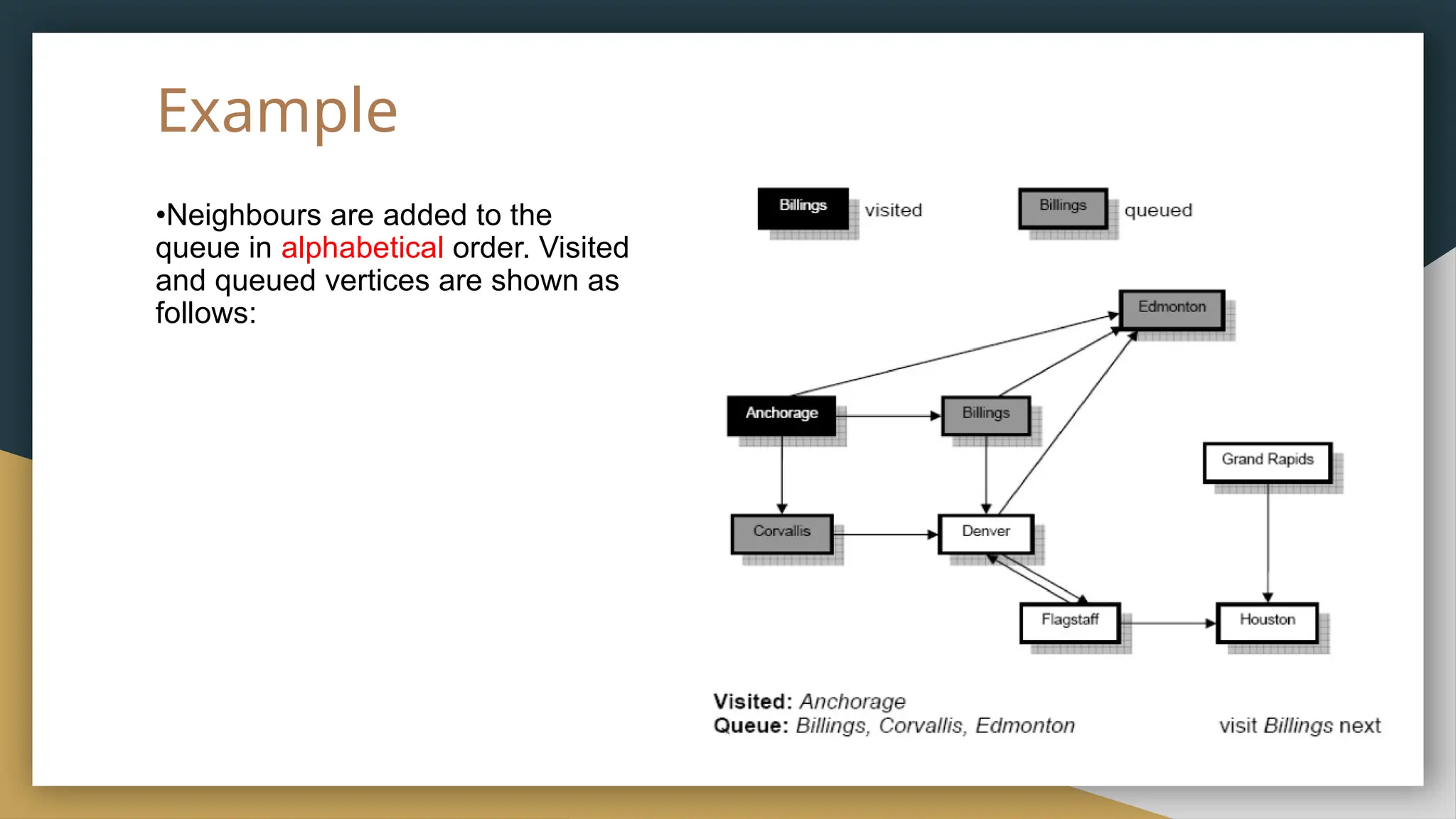
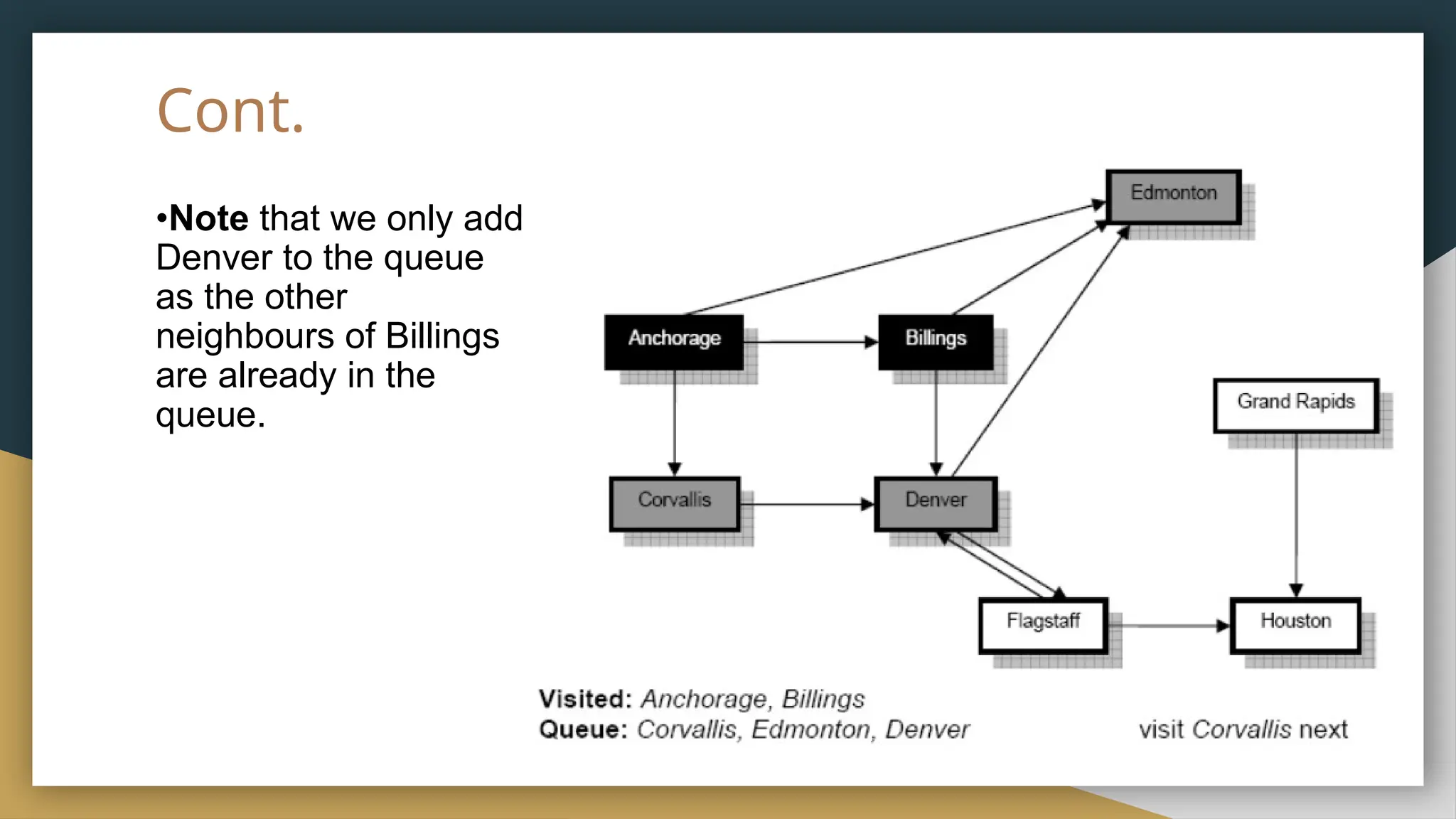
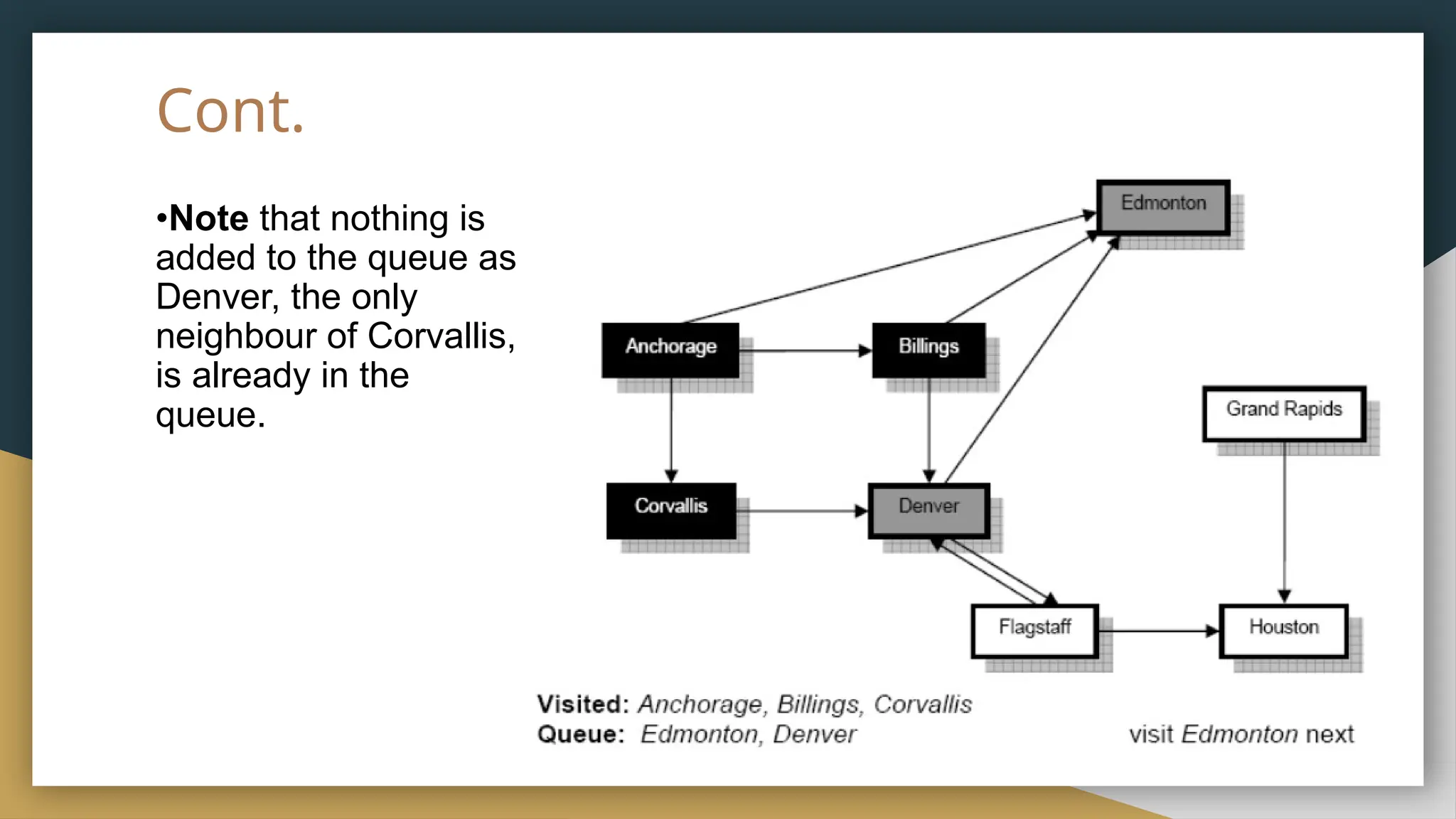
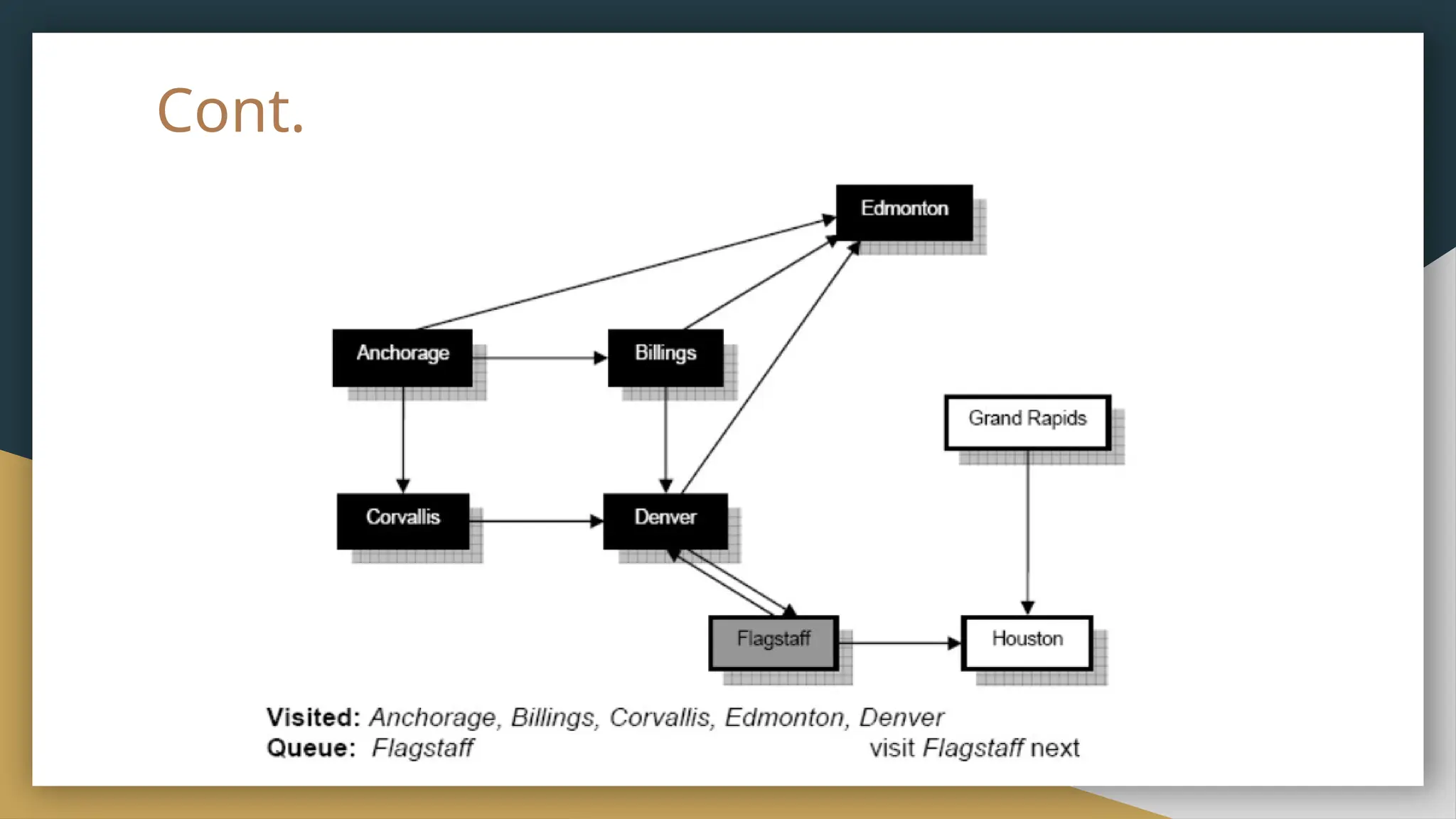
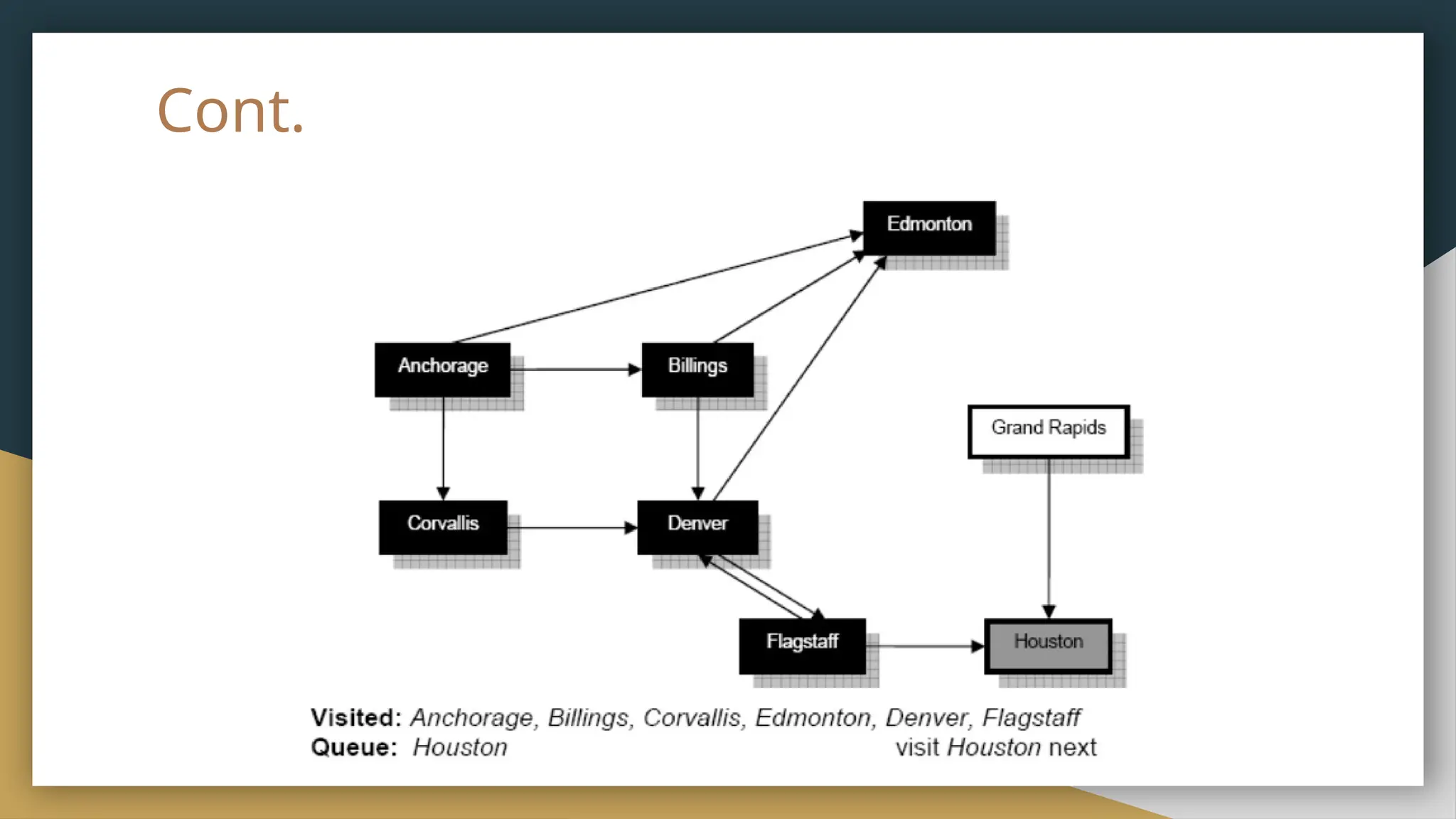
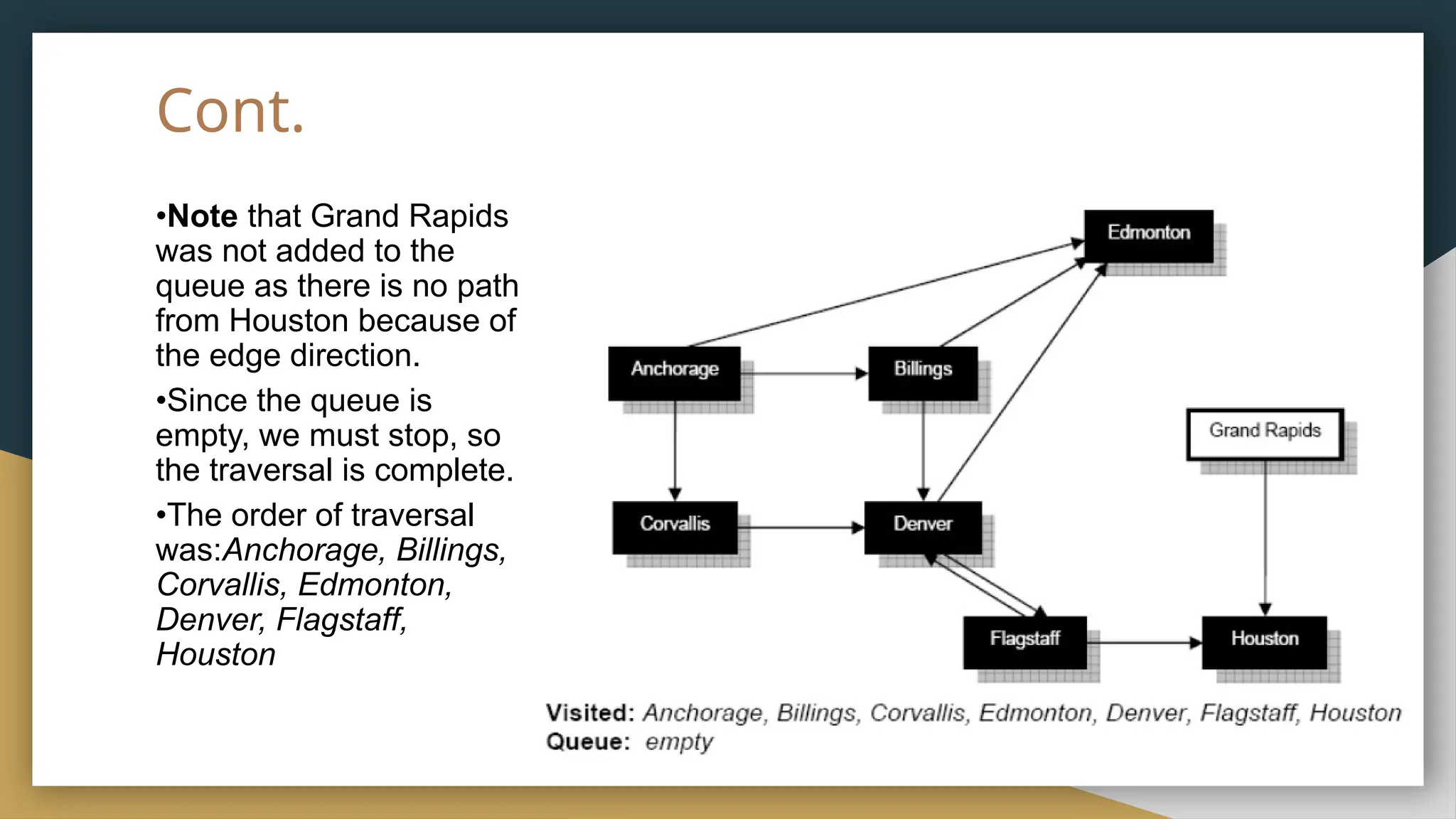
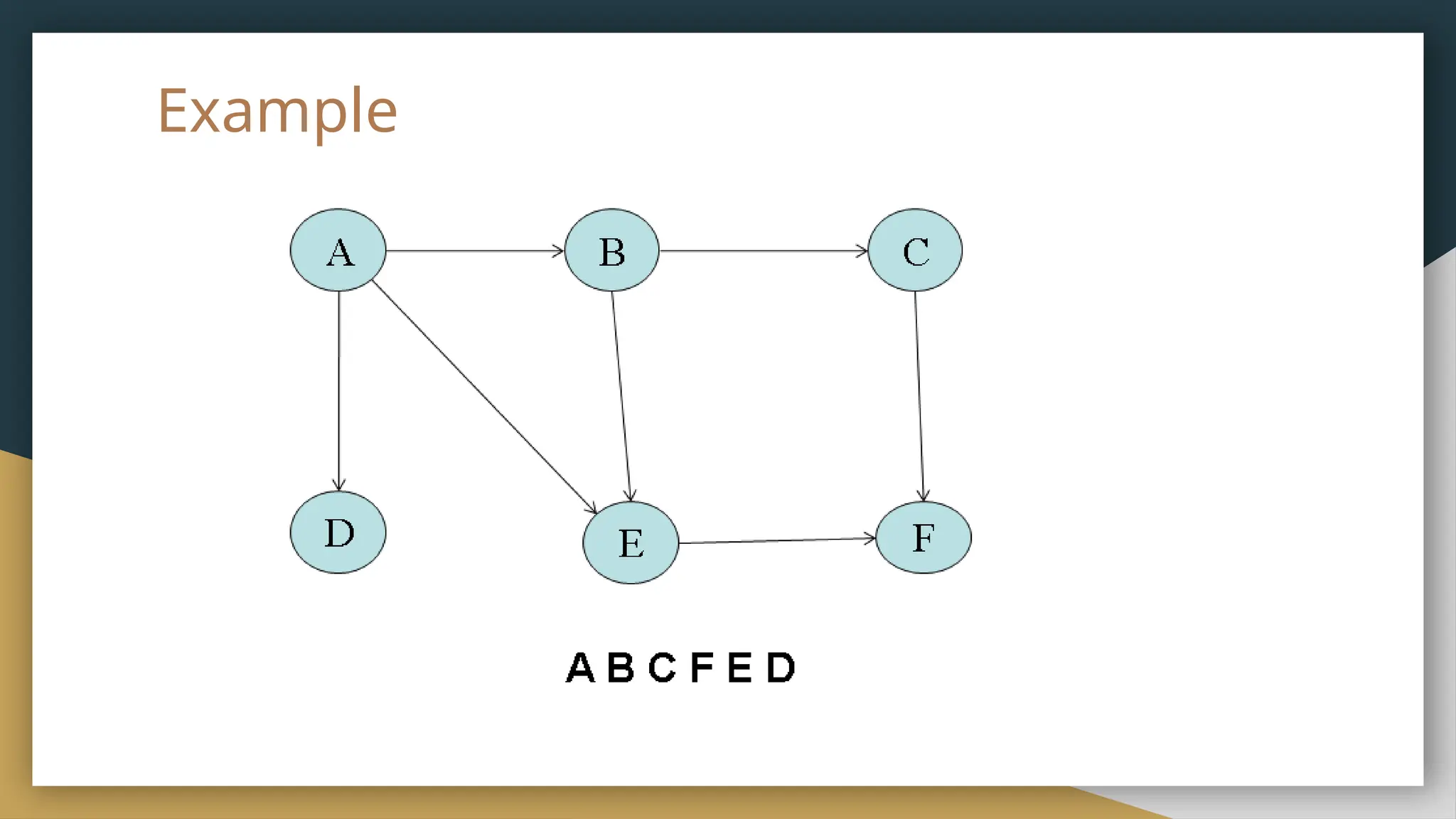
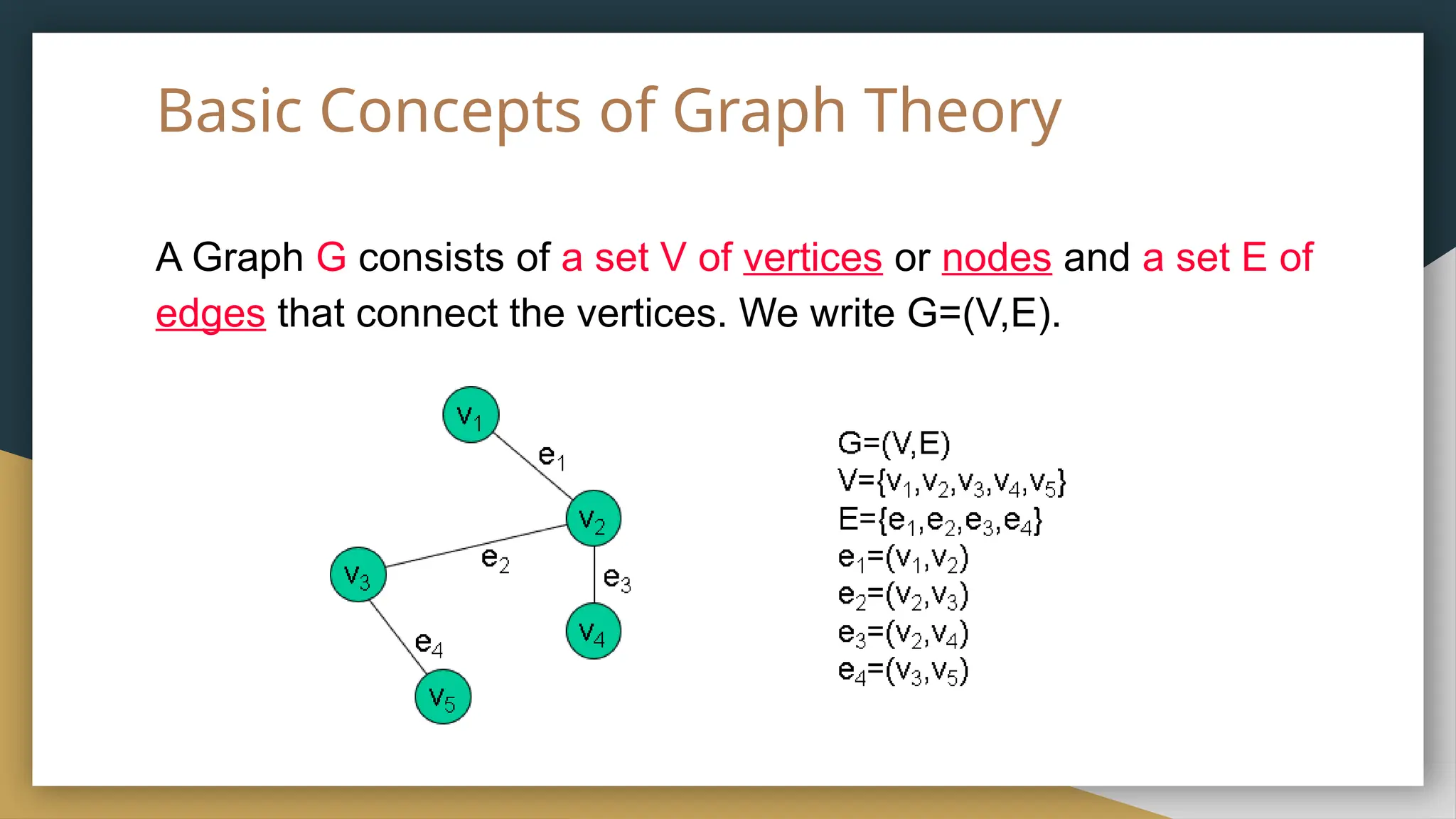
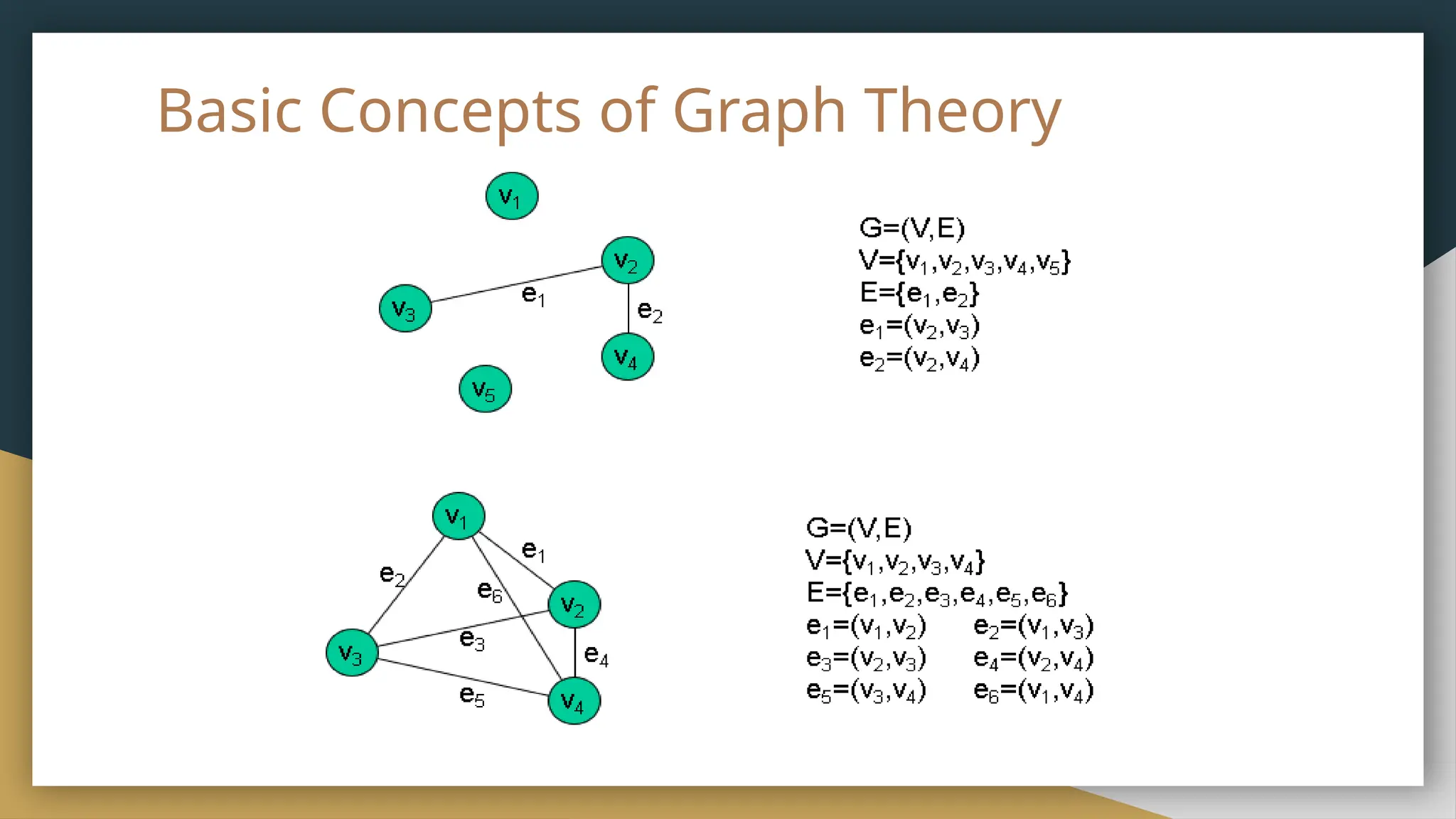
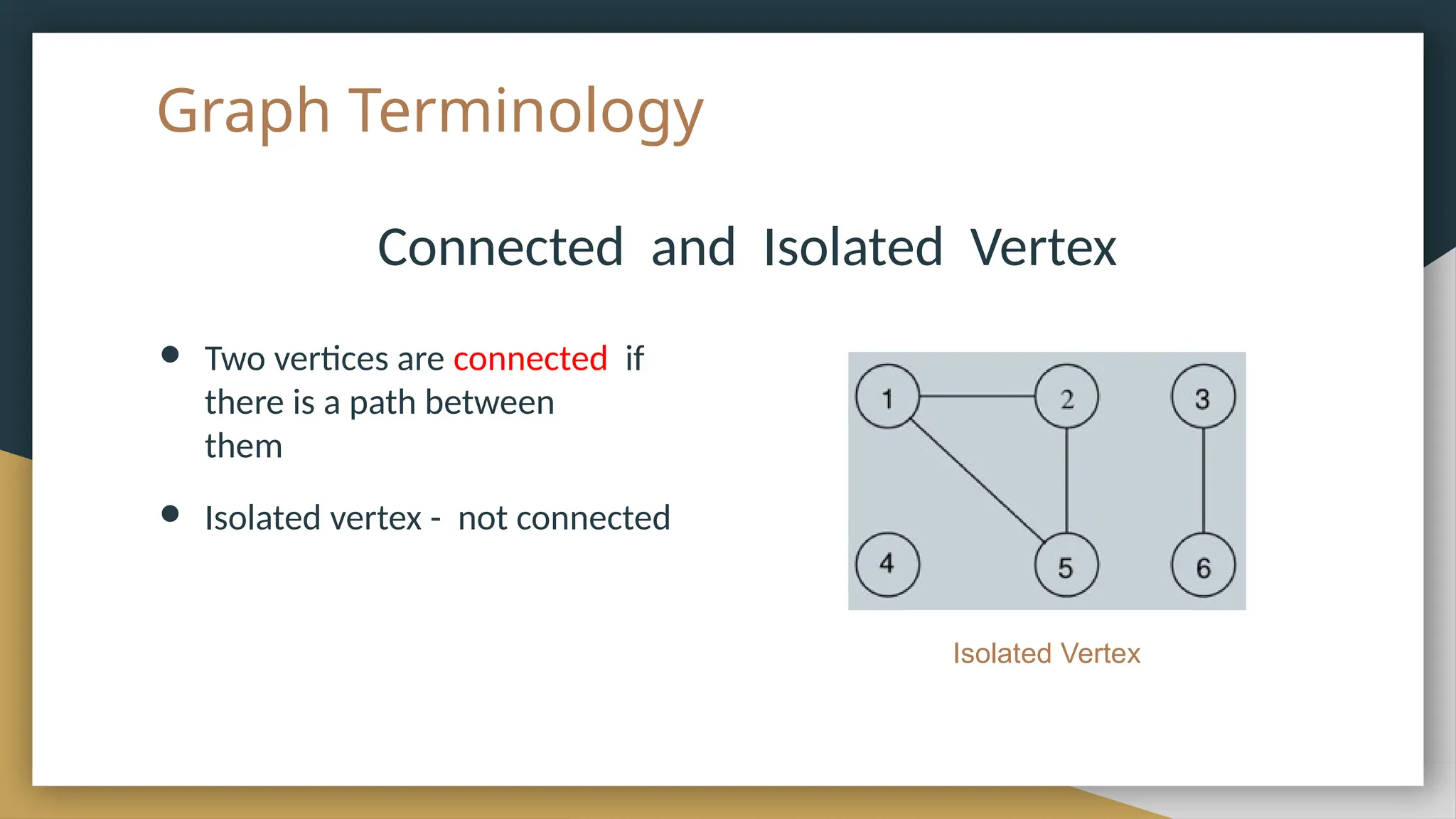
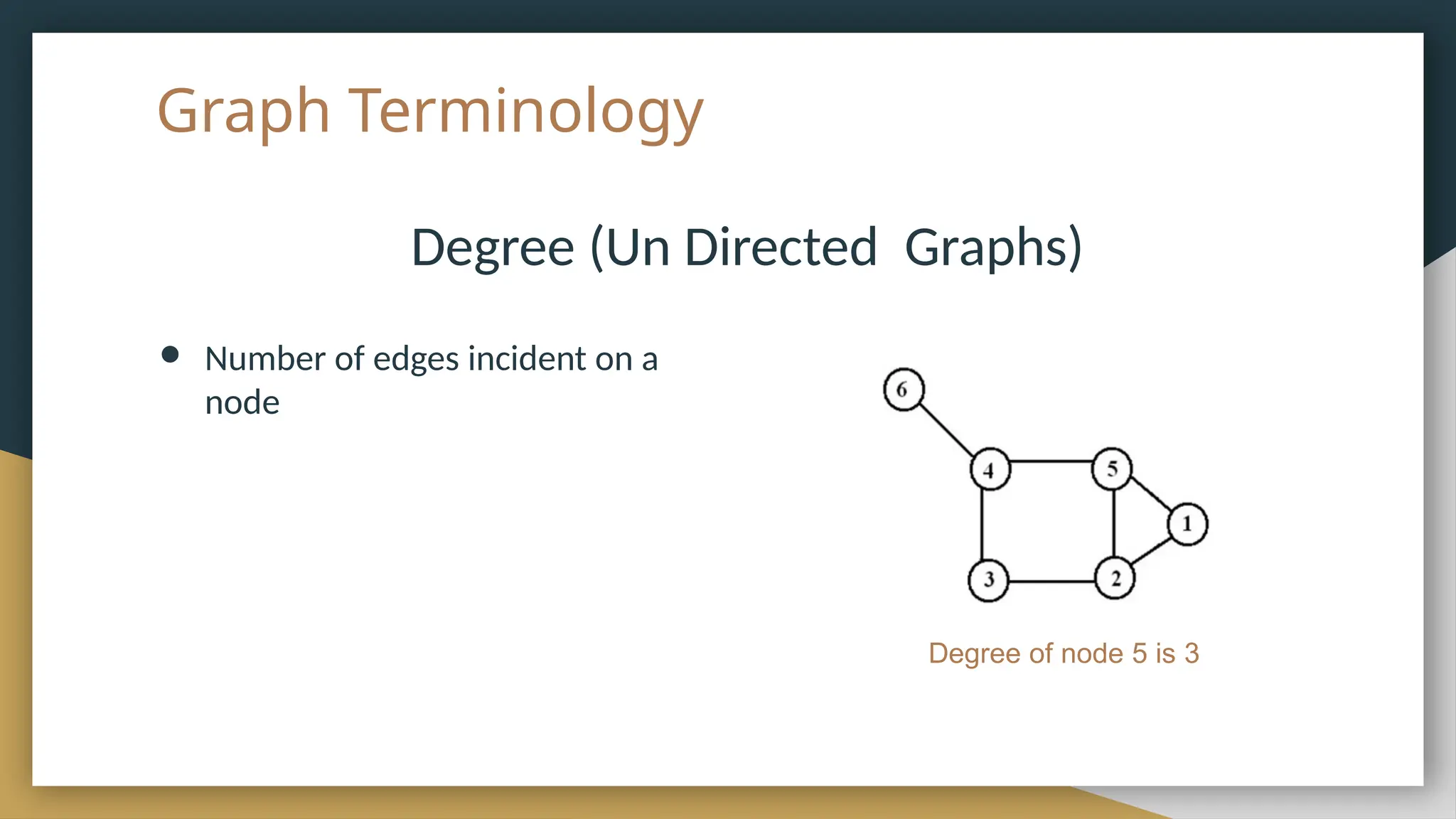
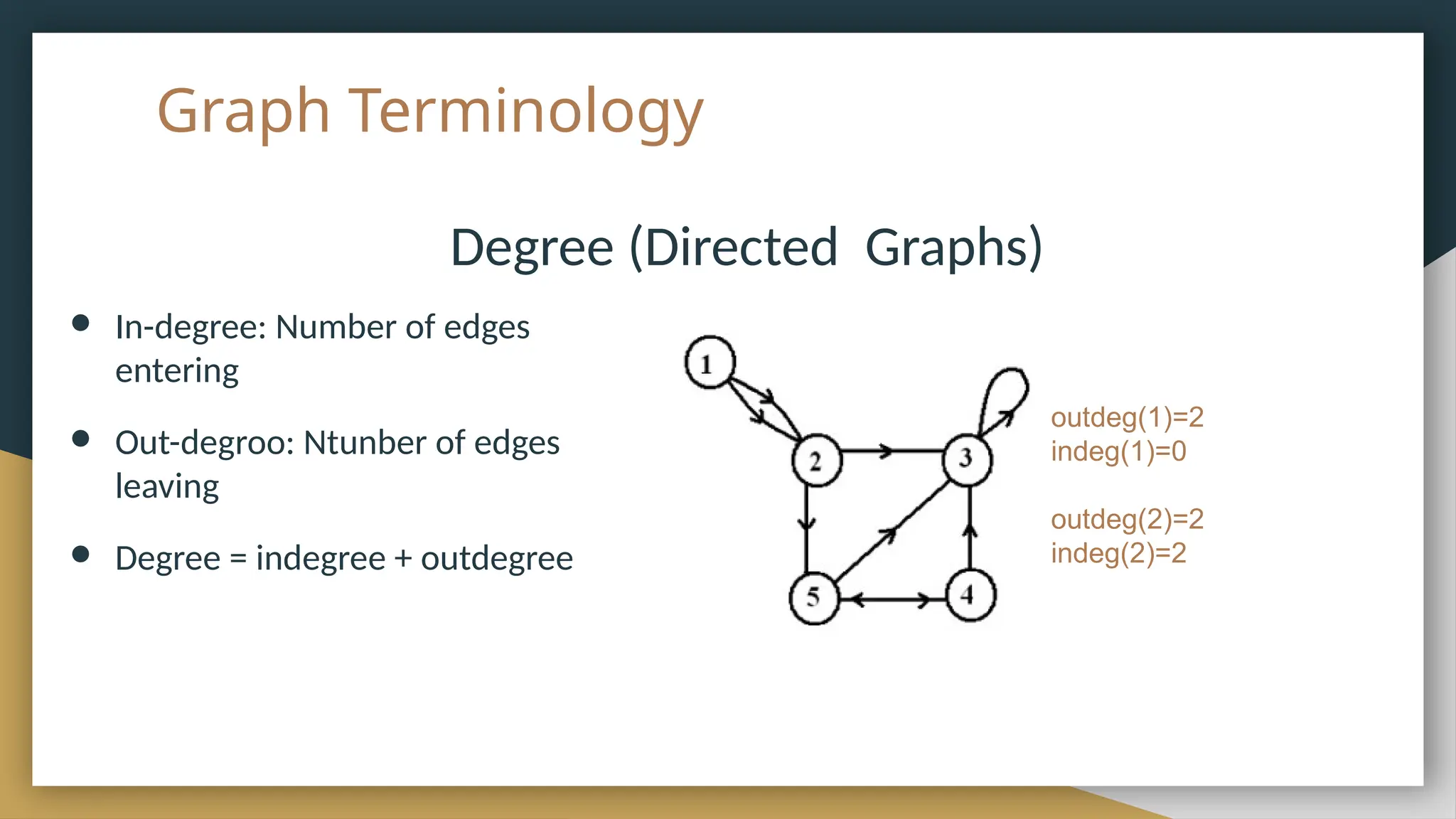
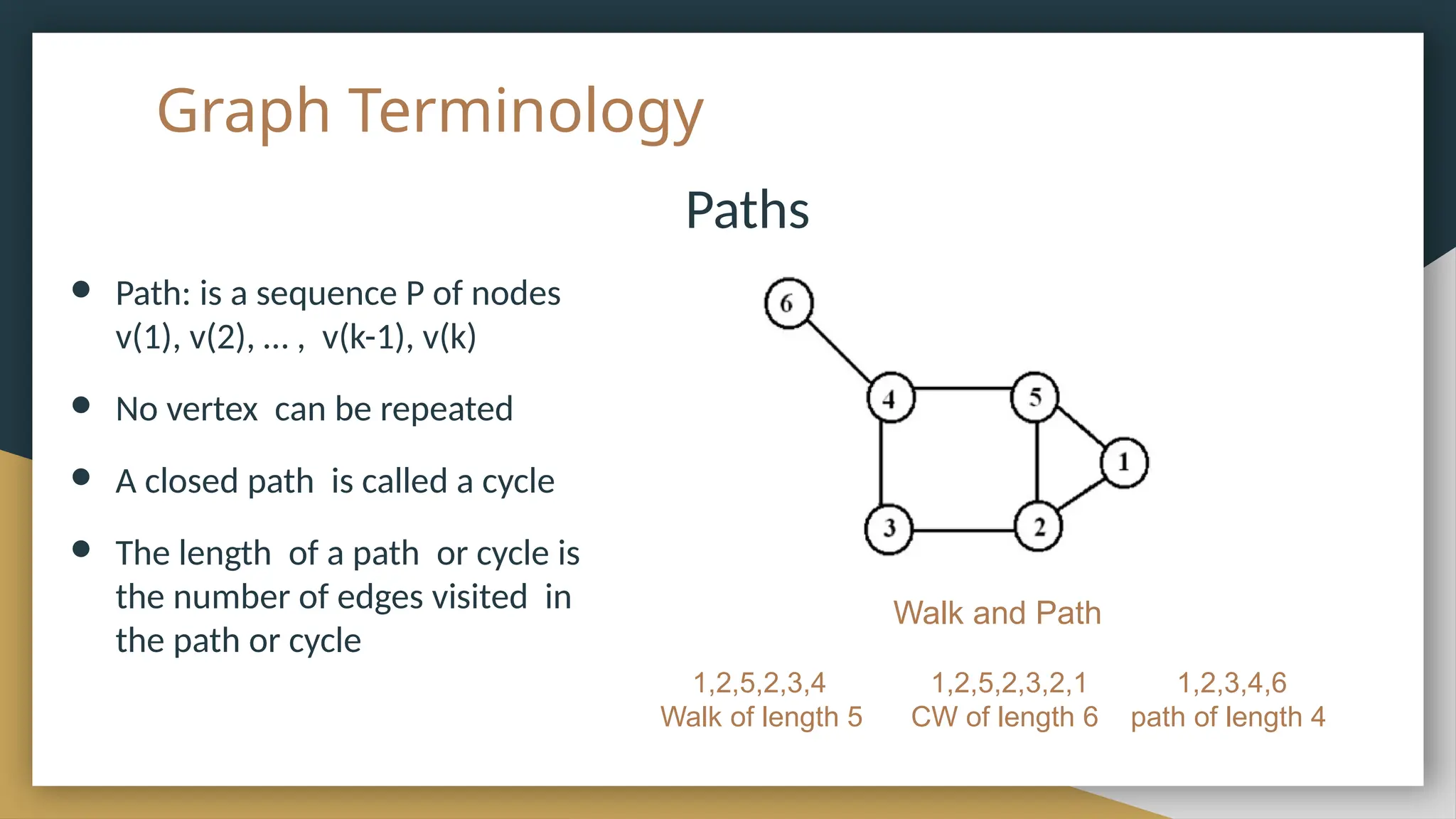
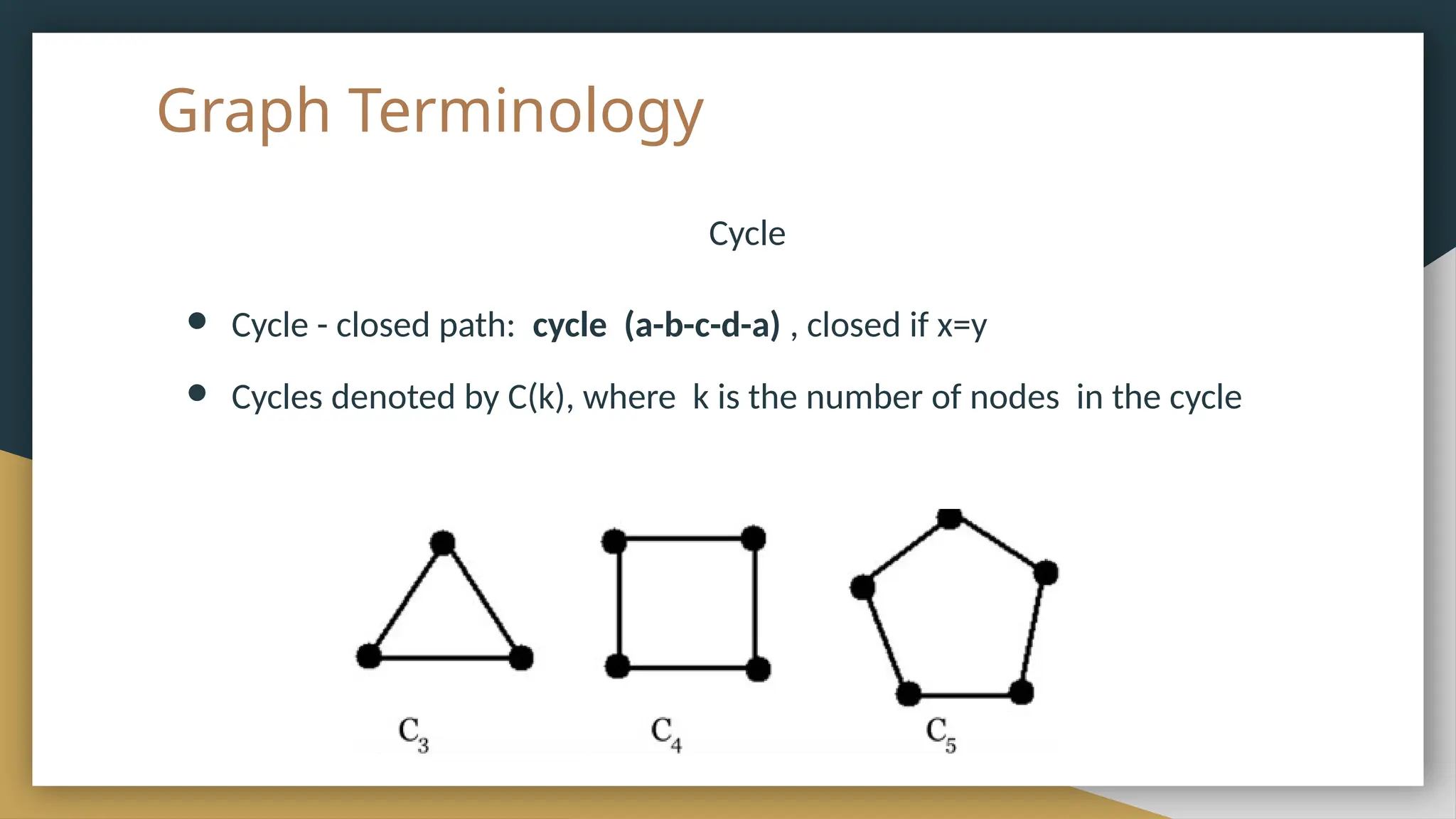
The document provides an overview of graph theory, detailing its history, applications, basic concepts, terminologies, and representation methods. It traces the origins of graph theory back to Euler's work and highlights various applications in fields such as transportation, electronic circuits, and computer networks. The document also explains essential graph concepts like vertices, edges, cycles, paths, and traversal methods including breadth-first and depth-first search.

1. Graph Data Structure
By :
I Kadek Agus Wahyu Raharja (23219019)
Arief Nur Rahman (23219034)

2. Outline
1. History of Graph Theory
2. Application of Graph
3. Basic Concepts of Graph Theory
4. Graph Terminology
5. Representation of Graph

3. History of Graph Theory
The origin of graph theory can be traced back to Euler's work on
the Konigsberg bridges problem (1735), which led to the
concept of an Eulerian graph. The study of cycles on
polyhedra by the Thomas P. Kirkman (1806 - 95) and William
R Hamilton (1805-65) led to the concept of a Hamiltonian
graph.

4. History of Graph Theory
● Begun in 1735
● Mentioned in Leonhard Euler's paper on
"Seven Bridges of Konigsberg".
● Problem : Walk all 7 bridges without
crossing a bridge twice

5. History of Graph Theory
● Cycles in Polyhedra - polyhedron with no
Hamiltonian cycle
Thomas P.
Kirkman
William R.
Hamilton

6. Application of Graph
● In many cases we are faced with a problem that is defined in terms of a number
of objects or entities that have some relationships among them. We then try to
answer interesting questions.
○ Flight scheduling
○ Traveling
○ Circuit layout, etc
● Graphs are the basic mathematical formulation we use too tackle such problems.
○ Basic definitions and properties.
○ Computer representation.
○ Some applications.

7. Application of Graph
● Electronic circuits
○ Printed circuit board
○ Integrated circuit
● Transportation networks
○ Highway network
○ Flight network
● Computer networks
○ Local area network
○ Wide area network
○ Internet
● Databases
○ Entity-relationship diagram

8. Basic Concepts of Graph Theory
A Graph G consists of a set V of vertices or nodes and a set E of
edges that connect the vertices. We write G=(V,E).

9. Basic Concepts of Graph Theory

10. Graph Terminology
Classification of Graph Terms
1. Global terms refer to a whole graph
2. Local terms refer to a single node in a graph

11. Graph Terminology
Connected and Isolated Vertex
● Two vertices are connected if
there is a path between
them
● Isolated vertex - not connected
Isolated Vertex

12. Graph Terminology
Adjacent nodes
● Two nodes are adjacent if they are connected via an edge.
● If edge e={u,v} ϵ E(G), we say that u and v are adjacent or neighbors
● An edge where the two end vertices are the same is called a loop, or
a self-loop

13. Graph Terminology
Degree (Un Directed Graphs)
● Number of edges incident on a
node
Degree of node 5 is 3

14. Graph Terminology
Degree (Directed Graphs)
● In-degree: Number of edges
entering
● Out-degroo: Ntunber of edges
leaving
● Degree = indegree + outdegree
outdeg(1)=2
indeg(1)=0
outdeg(2)=2
indeg(2)=2

15. Graph Terminology
Walk
● trail: no edge can be repeat
a-b-c-d-e-b-d
● walk: a path in which edges/no can be repeated
a-b-d-a-b-c
● A walk is closed if a=c

16. Graph Terminology
Paths
● Path: is a sequence P of nodes
v(1), v(2), … , v(k-1), v(k)
● No vertex can be repeated
● A closed path is called a cycle
● The length of a path or cycle is
the number of edges visited in
the path or cycle
Walk and Path
1,2,5,2,3,4 1,2,5,2,3,2,1 1,2,3,4,6
Walk of length 5 CW of length 6 path of length 4

17. Graph Terminology
Cycle
● Cycle - closed path: cycle (a-b-c-d-a) , closed if x=y
● Cycles denoted by C(k), where k is the number of nodes in the cycle

18. Graph Terminology
Shortest Path
● Shortest Path is the path between two nodes that has the shortest
length
● Length - number of edges.
● Distance between u and v is the length of a shortest path between them
● The diameter of a graph is the length of the longest shortest path
between any pairs of nodes in the graph

19. Representation of Graph
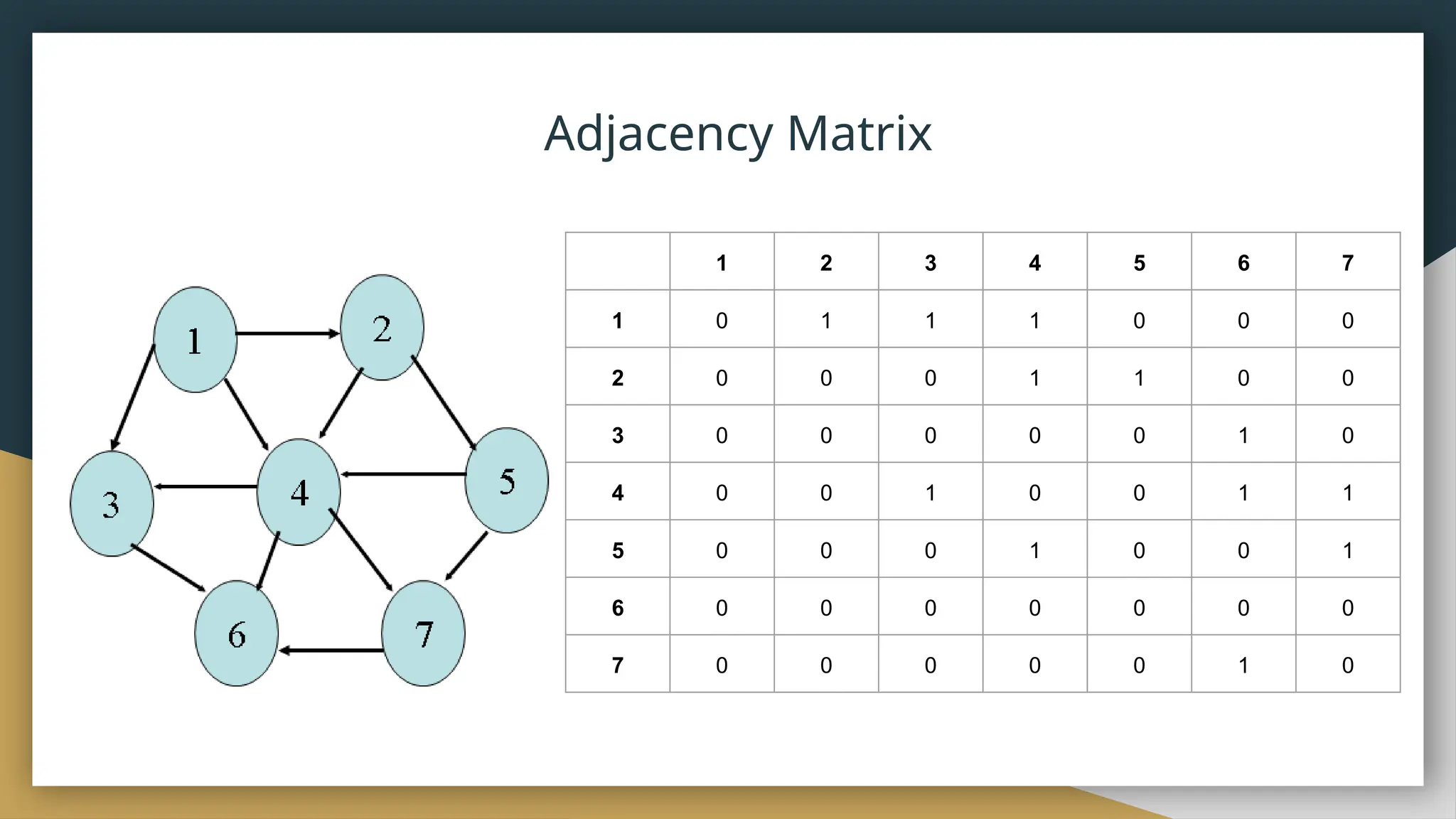
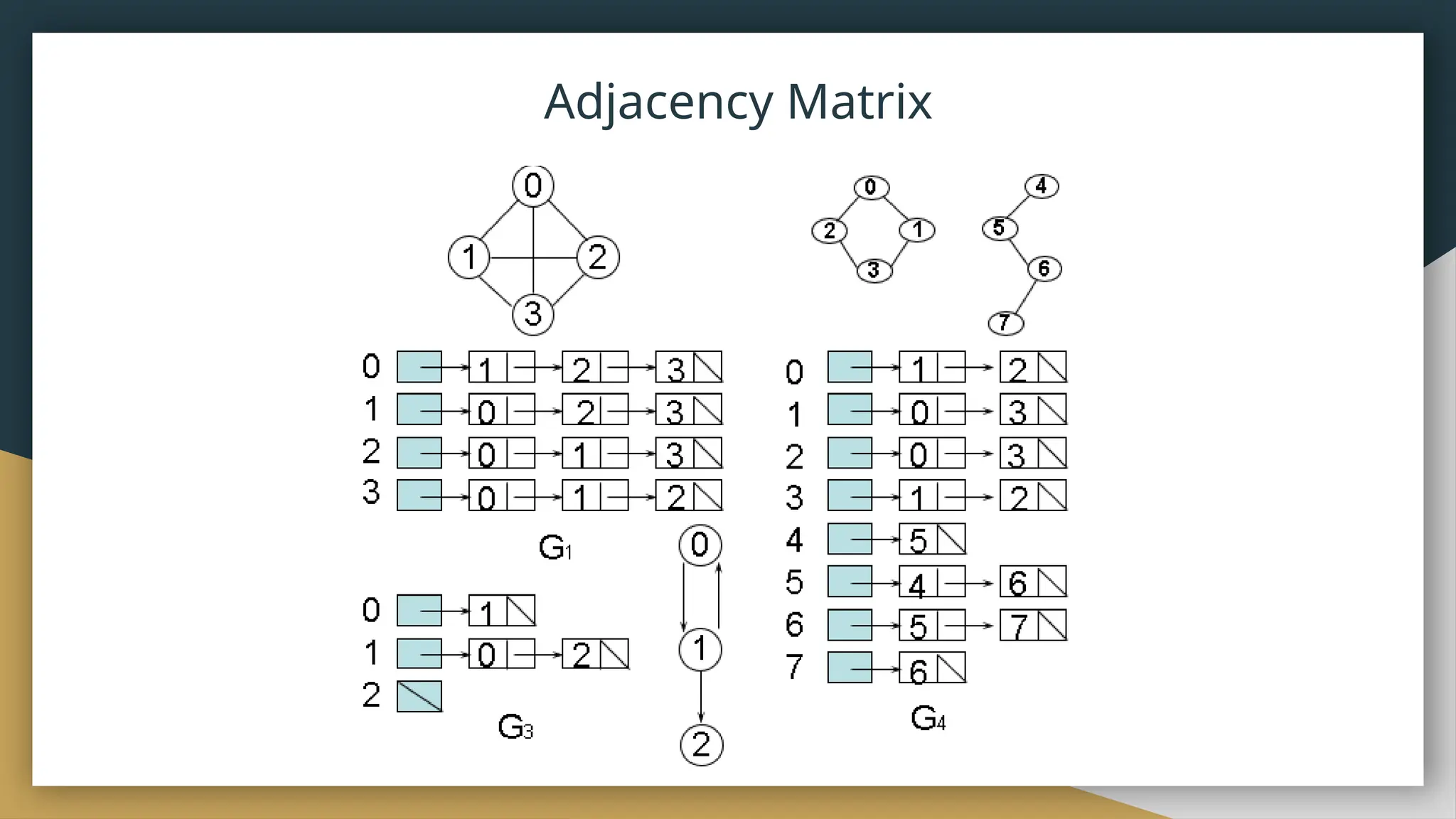
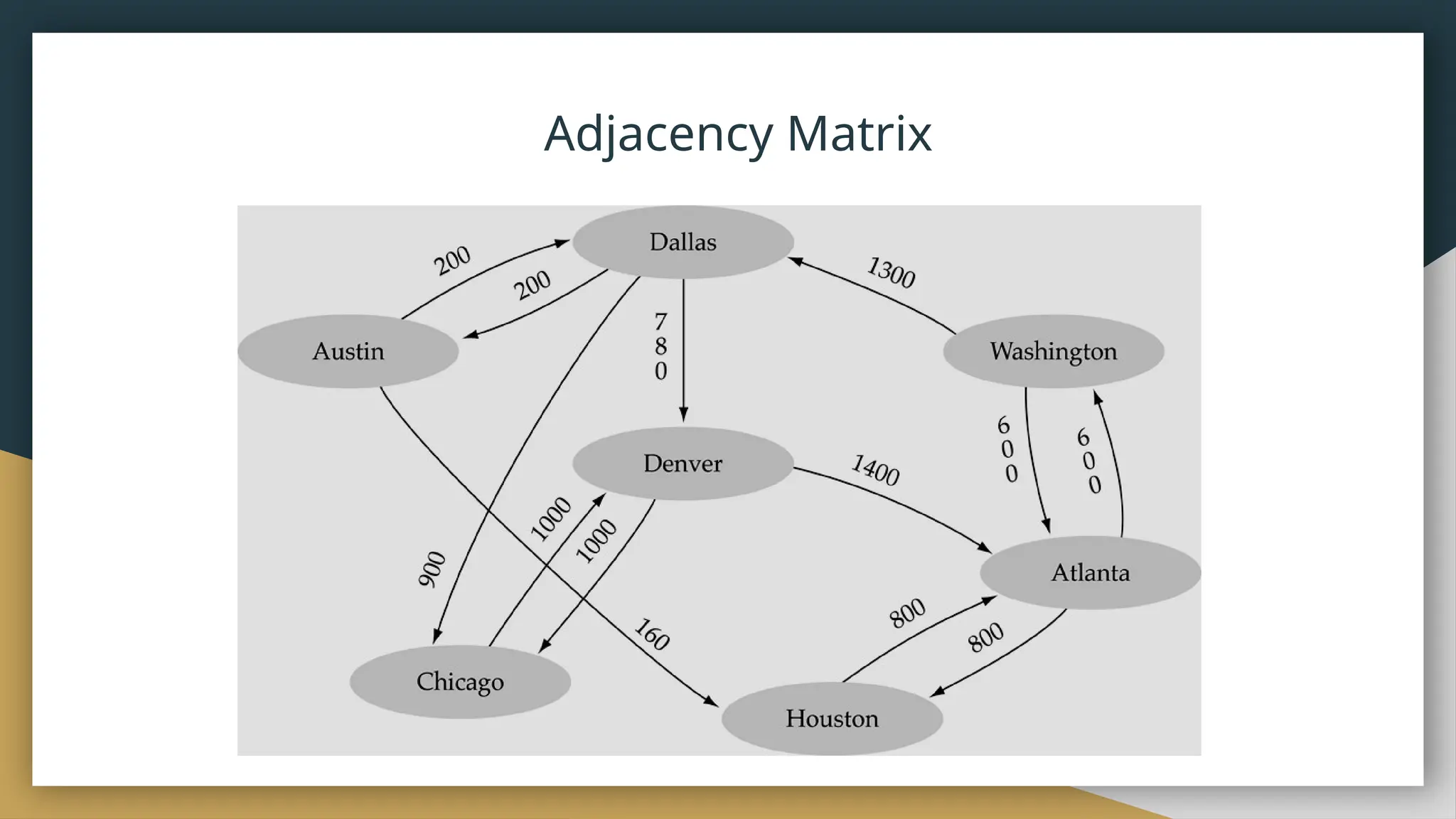
● The adjacency matrix for a graph G=(V,E) with n (or |V|) vertices
numbered 0, 1, …, n-1 is an n x n array M such that M[i][j] is 1 if
and only if there is an edge from vertex i to vertex j.
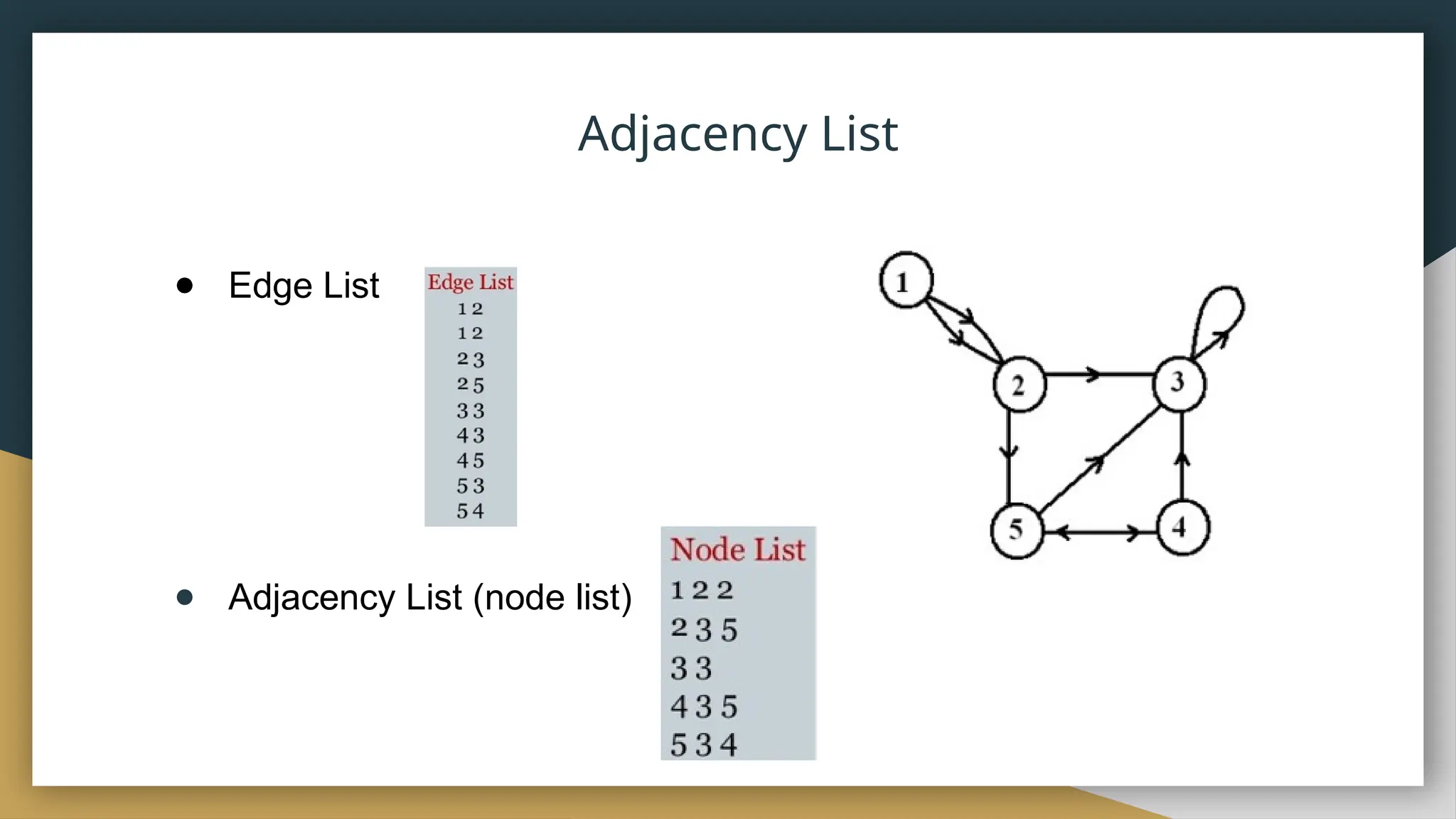
● The adjacency list for a graph G=(V,E) with n vertices numbered 0,
1, …, n-1 consists of n linked lists. The ith
linked list has a node for
vertex j if and only if the graph contains and edge from vertex i to
vertex j.

20. Adjacency Matrix
● Let G=(V,E) be a graph with n vertices.
● The adjacency matrix of G is a two-dimensional
n by n array, say adj_mat
● If the edge (vi, vj) is in E(G), adj_mat[i][j]=1
● If there is no such edge in E(G), adj_mat[i][j]=0
● The adjacency matrix for an undirected graph is symmetric; since
adj_mat[i][j]=adj_mat[j][i]
● The adjacency matrix for a digraph may not be symmetric

21. Adjacency Matrix

22. 1 2 3 4 5 6 7
1 0 1 1 1 0 0 0
2 0 0 0 1 1 0 0
3 0 0 0 0 0 1 0
4 0 0 1 0 0 1 1
5 0 0 0 1 0 0 1
6 0 0 0 0 0 0 0
7 0 0 0 0 0 1 0
Adjacency Matrix

23. •From the adjacency matrix, to determine the connection of vertices is
easy
•The degree of a vertex is
•We can also represent weighted graph with Adjacency Matrix. Now the
contents of the martix will not be 0 and 1 but the value is substituted with
the corresponding weight.
Adjacency Matrix

24. ● A Single Dimension array of Structure is used to represent the
vertices
● A Linked list is used for each vertex V which contains the vertices
which are adjacent from V (adjacency list)
Adjacency Matrix

25. Adjacency Matrix

26. Adjacency Matrix

27. Adjacency Matrix

28. ● Edge List
● Adjacency List (node list)
Adjacency List

29. Graph Traversal
•Traversal is the facility to move through a structure visiting each
of the vertices once.
•We looked previously at the ways in which a binary tree can be
traversed. Two of the traversal methods for a graph are breadth-
first and depth-first.

30. Breadth-First Graph Traversal
•This method visits all the vertices, beginning with a specified start vertex. It
can be described roughly as “neighbours-first”.
•No vertex is visited more than once, and vertices are visited only if they
can be reached – that is, if there is a path from the start vertex.
•Breadth-first traversal makes use of a queue data structure. The queue
holds a list of vertices which have not been visited yet but which should be
visited soon.
•Since a queue is a first-in first-out structure, vertices are visited in the order
in which they are added to the queue.
•Visiting a vertex involves, for example, outputting the data stored in that
vertex, and also adding its neighbours to the queue.
•Neighbours are not added to the queue if they are already in the queue, or
have already been visited.

31. Example
•Neighbours are added to the
queue in alphabetical order. Visited
and queued vertices are shown as
follows:

32. Cont.
•Note that we only add
Denver to the queue
as the other
neighbours of Billings
are already in the
queue.

33. Cont.
•Note that nothing is
added to the queue as
Denver, the only
neighbour of Corvallis,
is already in the
queue.

34. Cont.

35. Cont.

36. Cont.
•Note that Grand Rapids
was not added to the
queue as there is no path
from Houston because of
the edge direction.
•Since the queue is
empty, we must stop, so
the traversal is complete.
•The order of traversal
was:Anchorage, Billings,
Corvallis, Edmonton,
Denver, Flagstaff,
Houston

37. Depth-First Traversal
1.Depth-first traversal of a graph:
2.Start the traversal from an arbitrary vertex;
3.Apply depth-first search;
4.When the search terminates, backtrack to the previous vertex of the
finishing point,
5.Repeat depth-first search on other adjacent vertices, then backtrack to
one level up.
6.Continue the process until all the vertices that are reachable from the
starting vertex are visited.
7.Repeat above processes until all vertices are visited.

38. Depth First Search Traversal
•This method visits all the vertices, beginning with a specified start
vertex.
•This strategy proceeds along a path from vertex V as deeply into the
graph as possible.
•This means that after visiting V, the algorithm tries to visit any unvisited
vertex adjacent to V.
•When the traversal reaches a vertex which has no adjacent vertex, it
back tracks and visits an unvisited adjacent vertex.
•Depth-first traversal makes use of a Stack data structure.

39. Example

40. Cont.