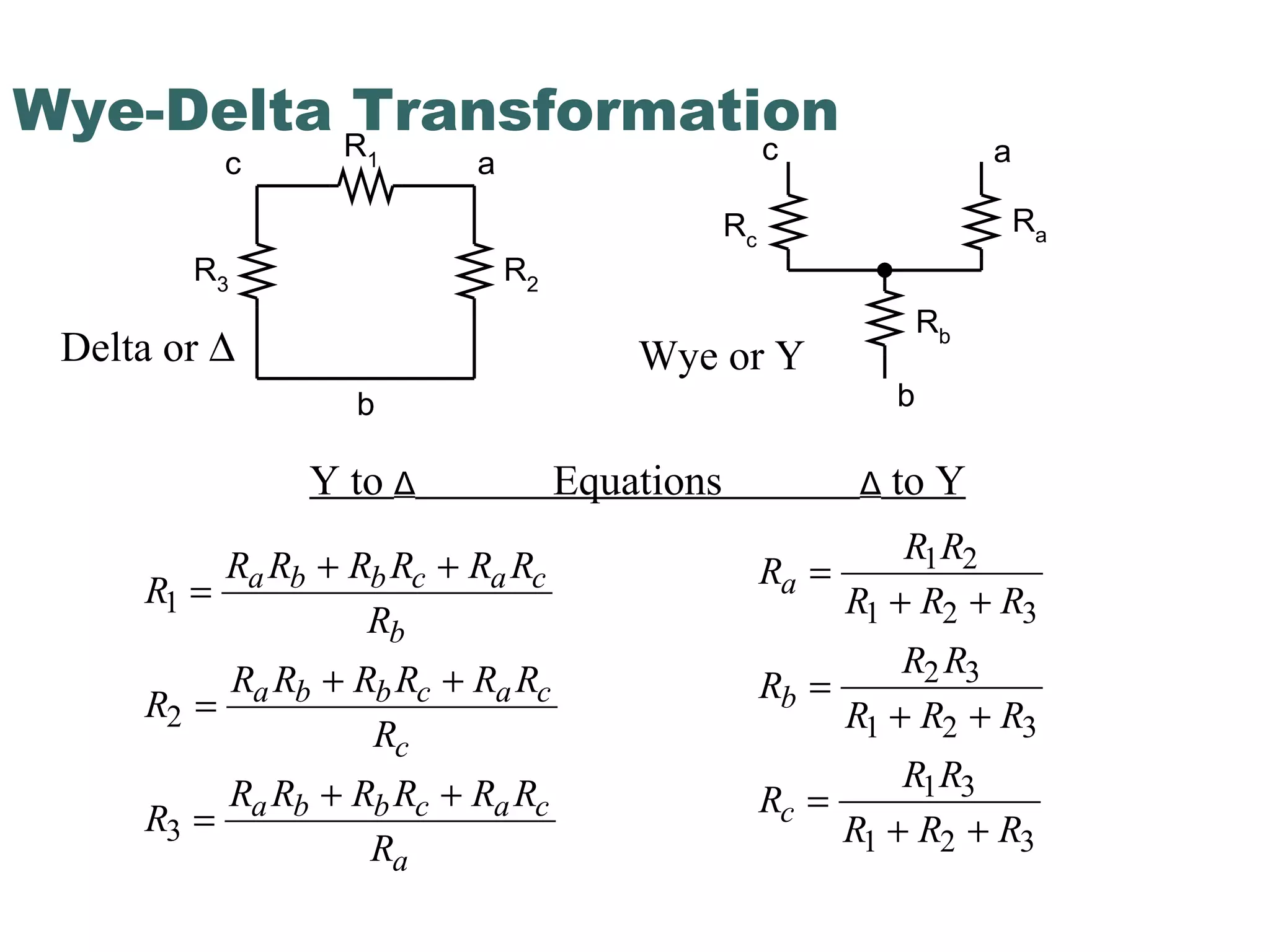
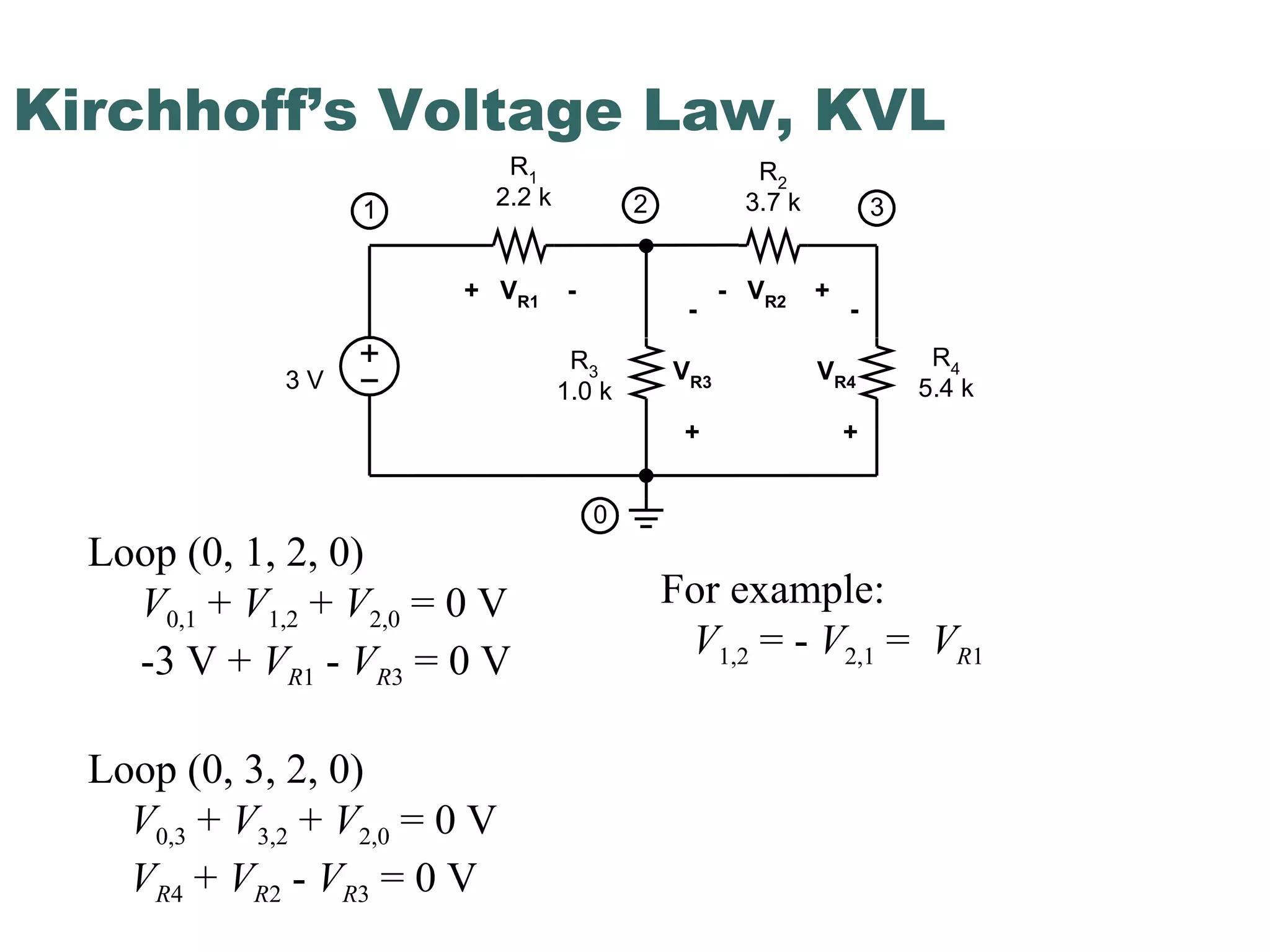
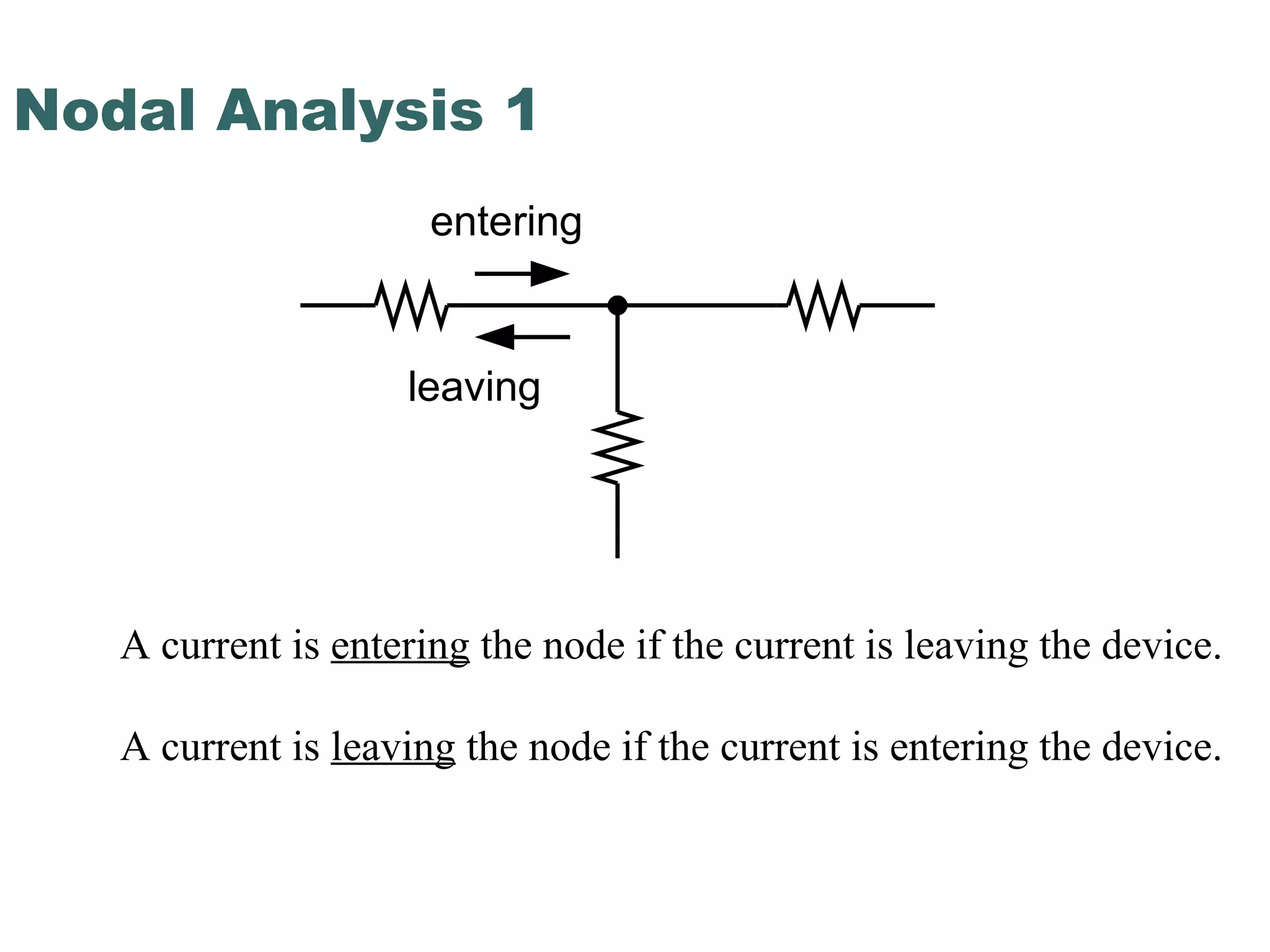
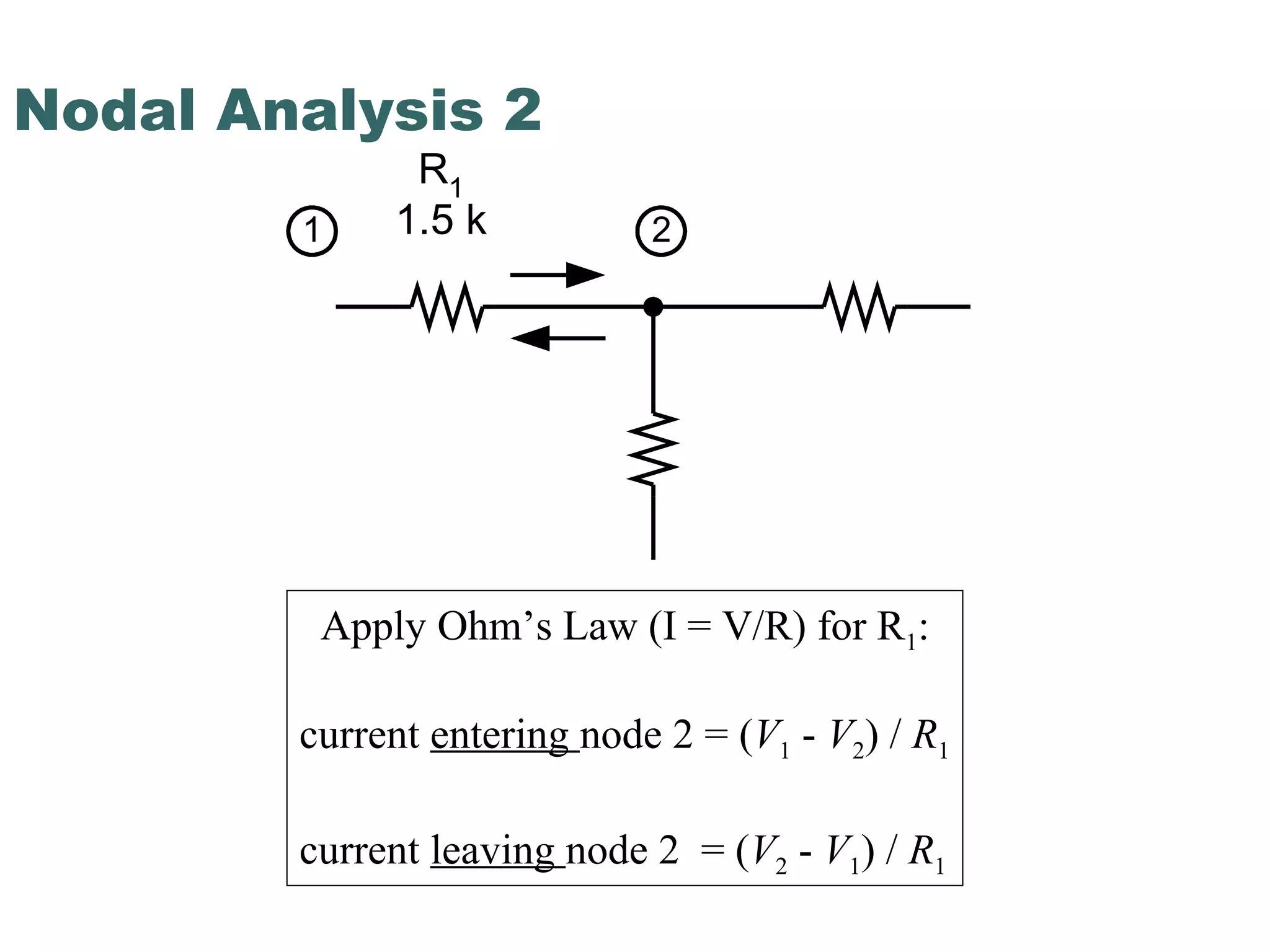
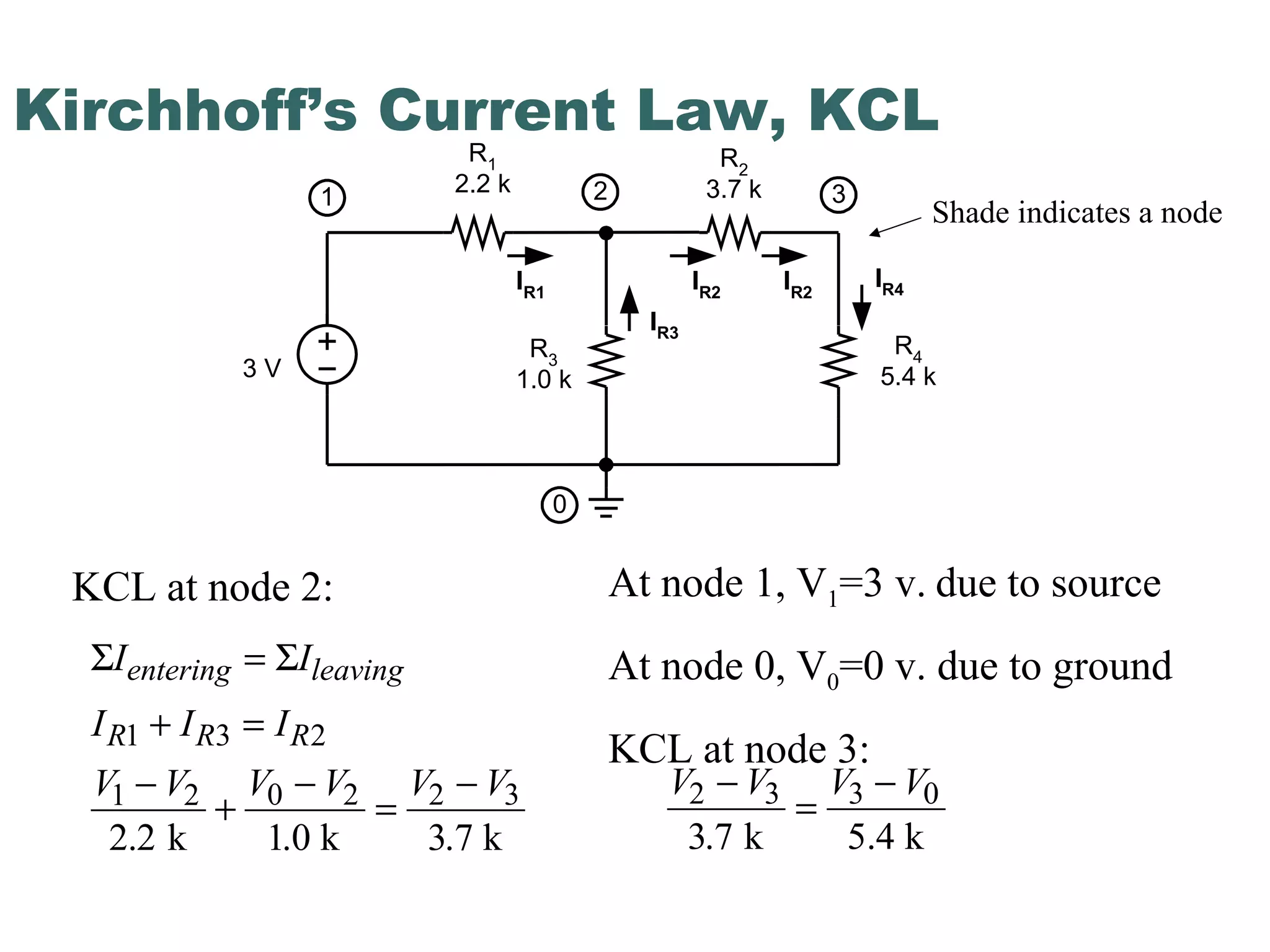
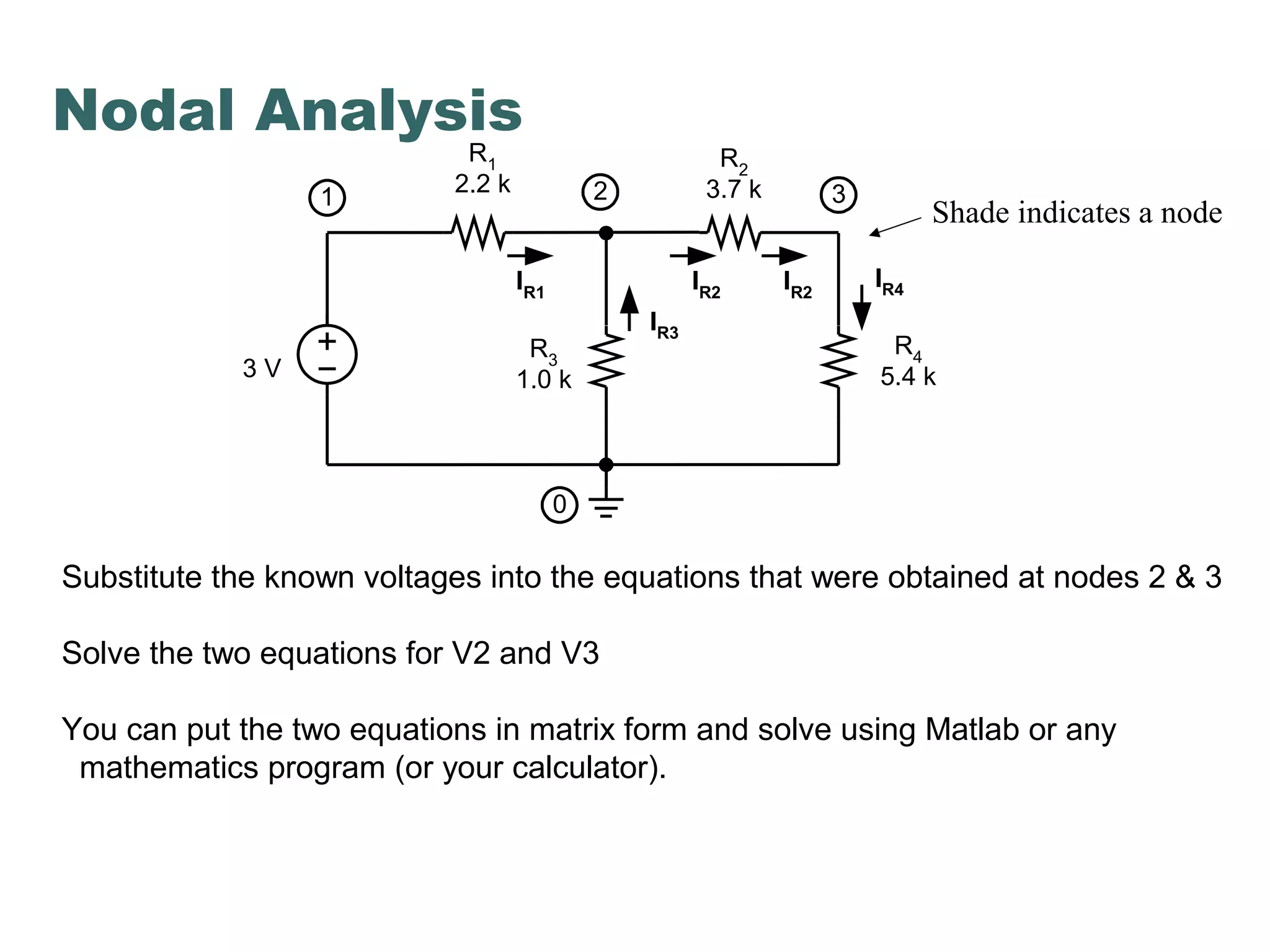
This document discusses nodal analysis, a technique for analyzing electrical circuits where the voltages at different nodes of the circuit are calculated. It provides examples of applying Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL) to set up equations relating the currents and voltages in a circuit containing resistors connected in a mesh. The document explains how to use these equations to solve for the unknown voltages at each node of the circuit.

1. Nodal analysis

2. Multisim Window

3. R1
R2
R3
c a
b
c a
b
Rc
Ra
Rb
Delta or ∆ Wye or Y
R
R R
R R R
R
R R
R R R
R
R R
R R R
a
b
c
=
+ +
=
+ +
=
+ +
1 2
1 2 3
2 3
1 2 3
1 3
1 2 3
Wye-Delta Transformation
R
R R R R R R
R
R
R R R R R R
R
R
R R R R R R
R
a b b c a c
b
a b b c a c
c
a b b c a c
a
1
2
3
=
+ +
=
+ +
=
+ +
Y to Δ Equations Δ to Y

4. Kirchhoff’s Voltage Law, KVL
3 V
R1
2.2 k
R2
3.7 k
R4
5.4 k
R3
1.0 k
1 2 3
0
+ VR1
- - VR2
+
-
VR4
+
-
VR3
+
Loop (0, 1, 2, 0)
V0,1 + V1,2 + V2,0 = 0 V
-3 V + VR1 - VR3 = 0 V
Loop (0, 3, 2, 0)
V0,3 + V3,2 + V2,0 = 0 V
VR4 + VR2 - VR3 = 0 V
For example:
V1,2 = - V2,1 = VR1

5. Nodal Analysis 1
entering
leaving
A current is entering the node if the current is leaving the device.
A current is leaving the node if the current is entering the device.

6. Nodal Analysis 2
Apply Ohm’s Law (I = V/R) for R1:
current entering node 2 = (V1 - V2) / R1
current leaving node 2 = (V2 - V1) / R1
R1
1.5 k1 2

7. Kirchhoff’s Current Law, KCL
KCL at node 2:
Σ ΣI I
I I I
V V V V V V
entering leaving
R R R
=
+ =
−
+
−
=
−
1 3 2
1 2 0 2 2 3
2 2 1 3. k .0 k .7 k
Shade indicates a node
At node 1, V1=3 v. due to source
At node 0, V0=0 v. due to ground
KCL at node 3:
V V V V2 3 3 0
3 7
−
=
−
. k 5.4 k
3 V
R1
2.2 k
R2
3.7 k
R4
5.4 k
R3
1.0 k
1 2 3
0
IR1
IR2
IR3
IR2
IR4

8. Nodal Analysis
Shade indicates a node
3 V
R1
2.2 k
R2
3.7 k
R4
5.4 k
R3
1.0 k
1 2 3
0
IR1
IR2
IR3
IR2
IR4
Substitute the known voltages into the equations that were obtained at nodes 2 & 3
Solve the two equations for V2 and V3
You can put the two equations in matrix form and solve using Matlab or any
mathematics program (or your calculator).