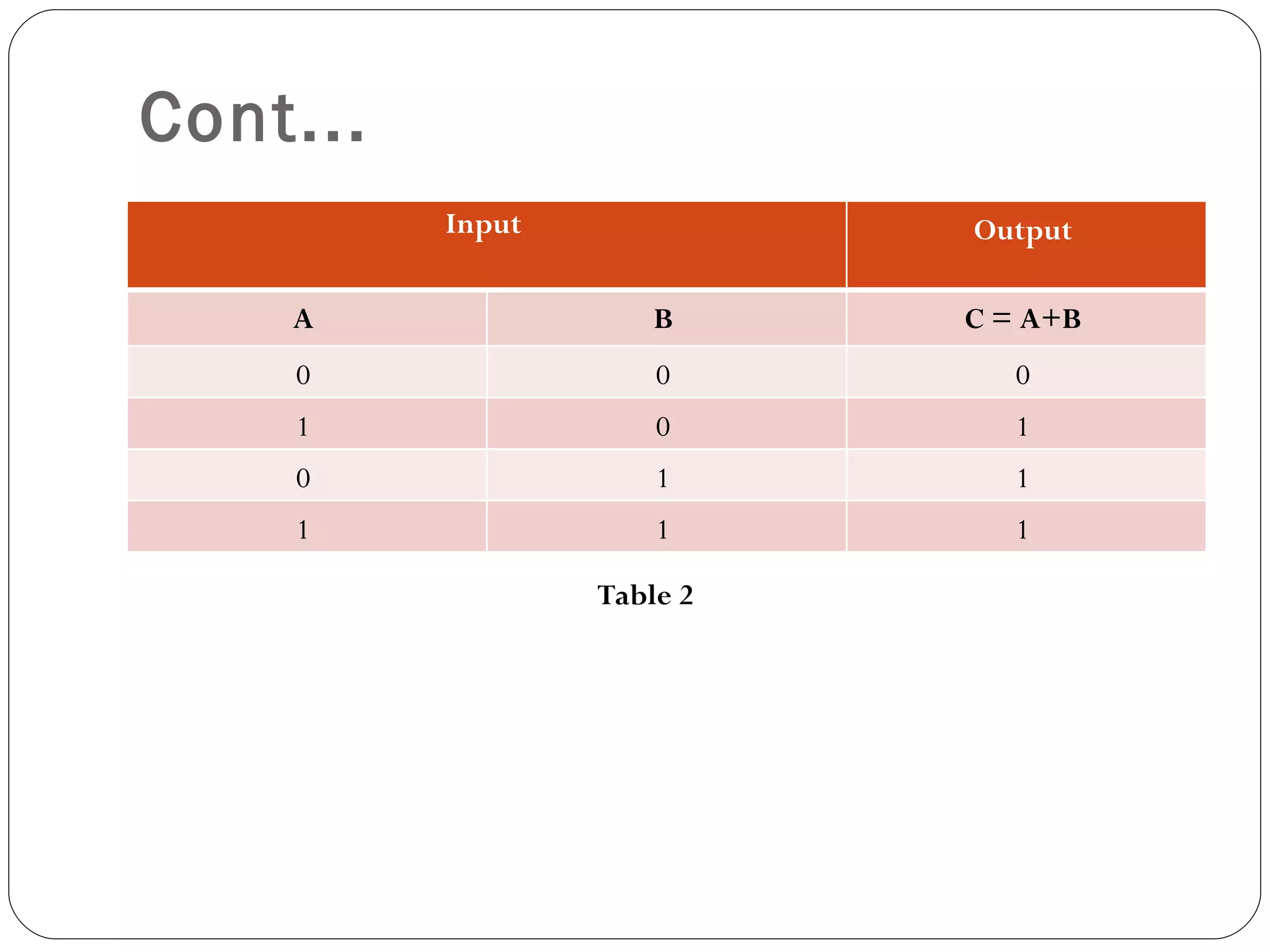
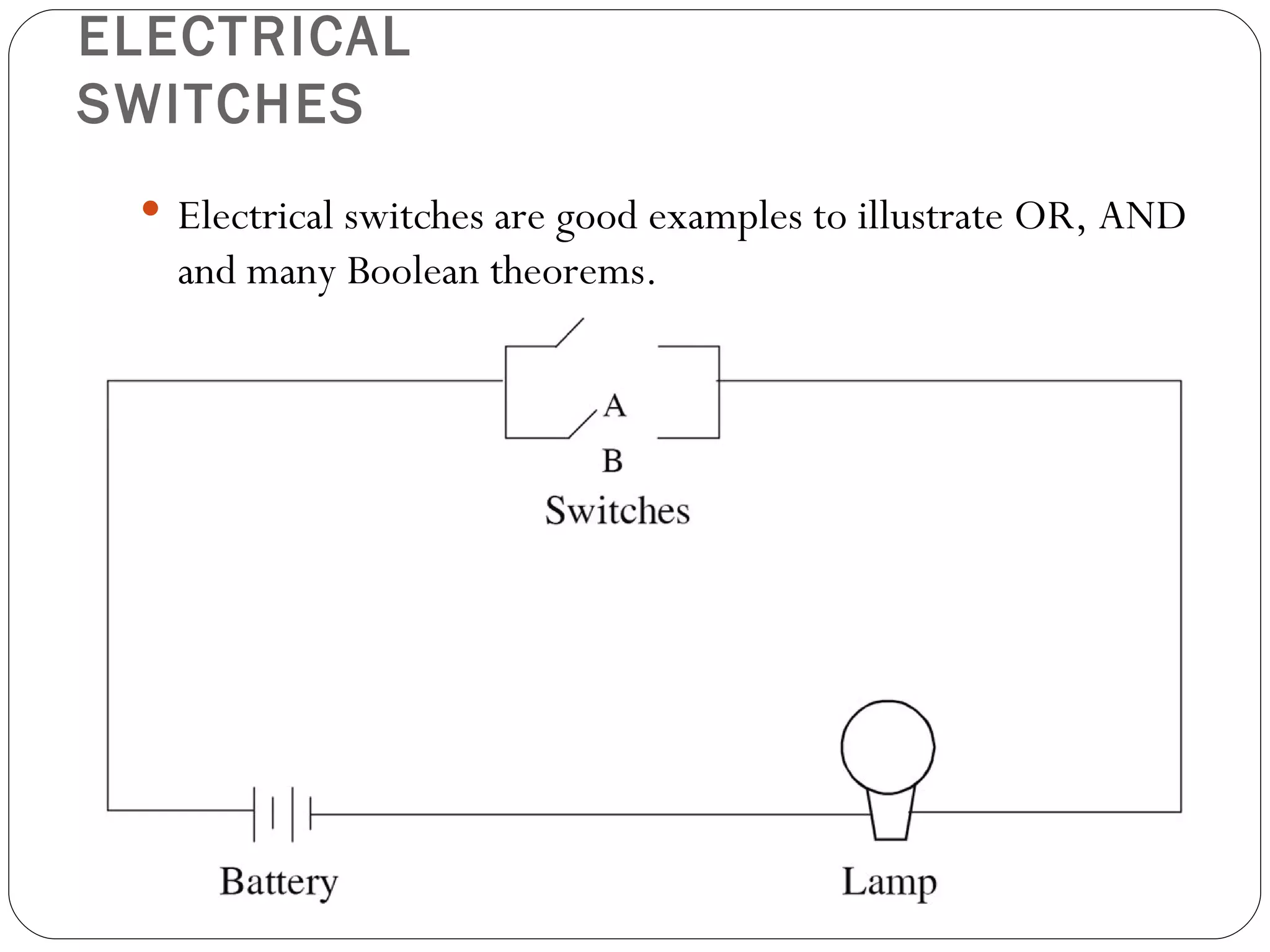
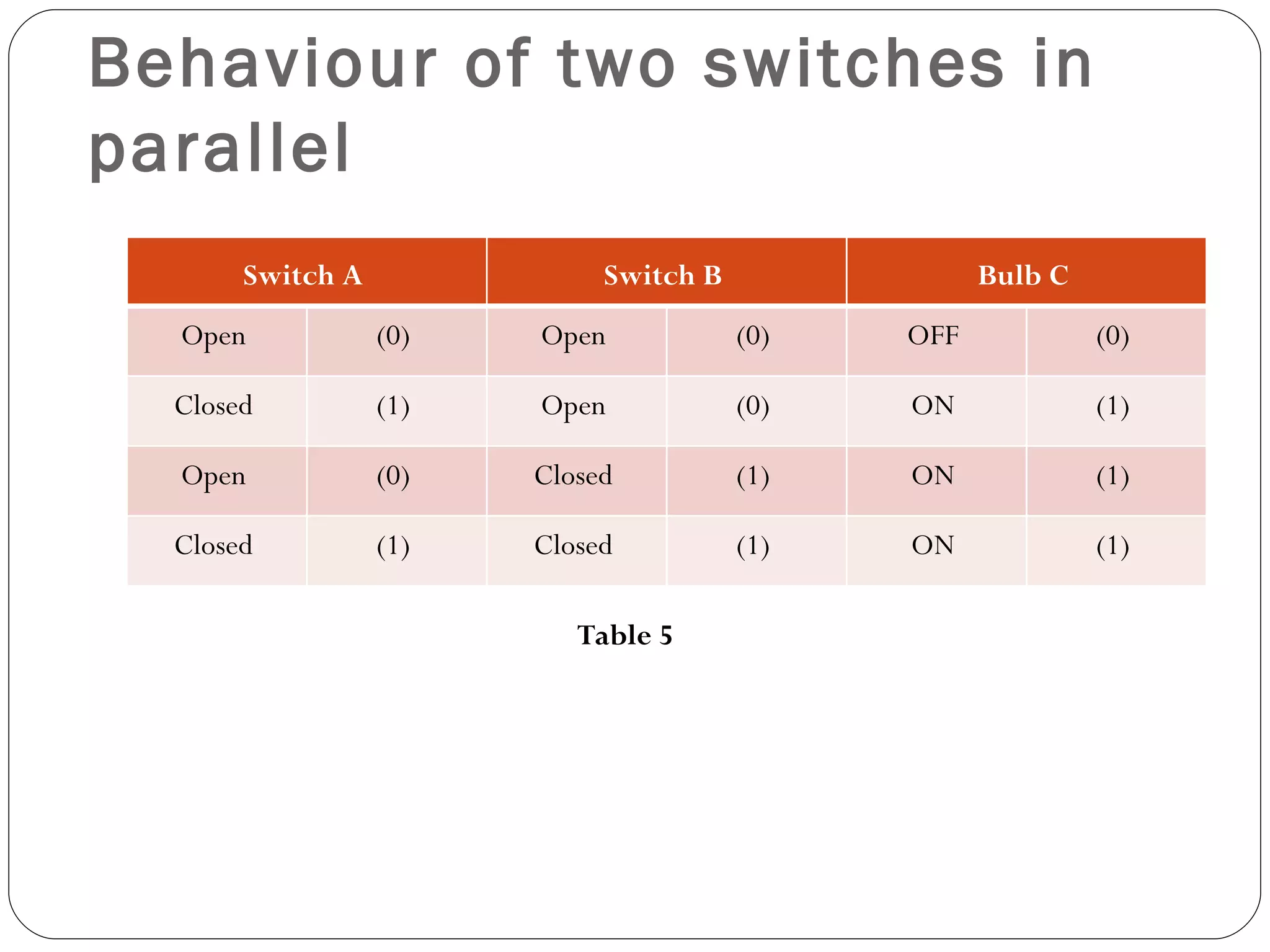
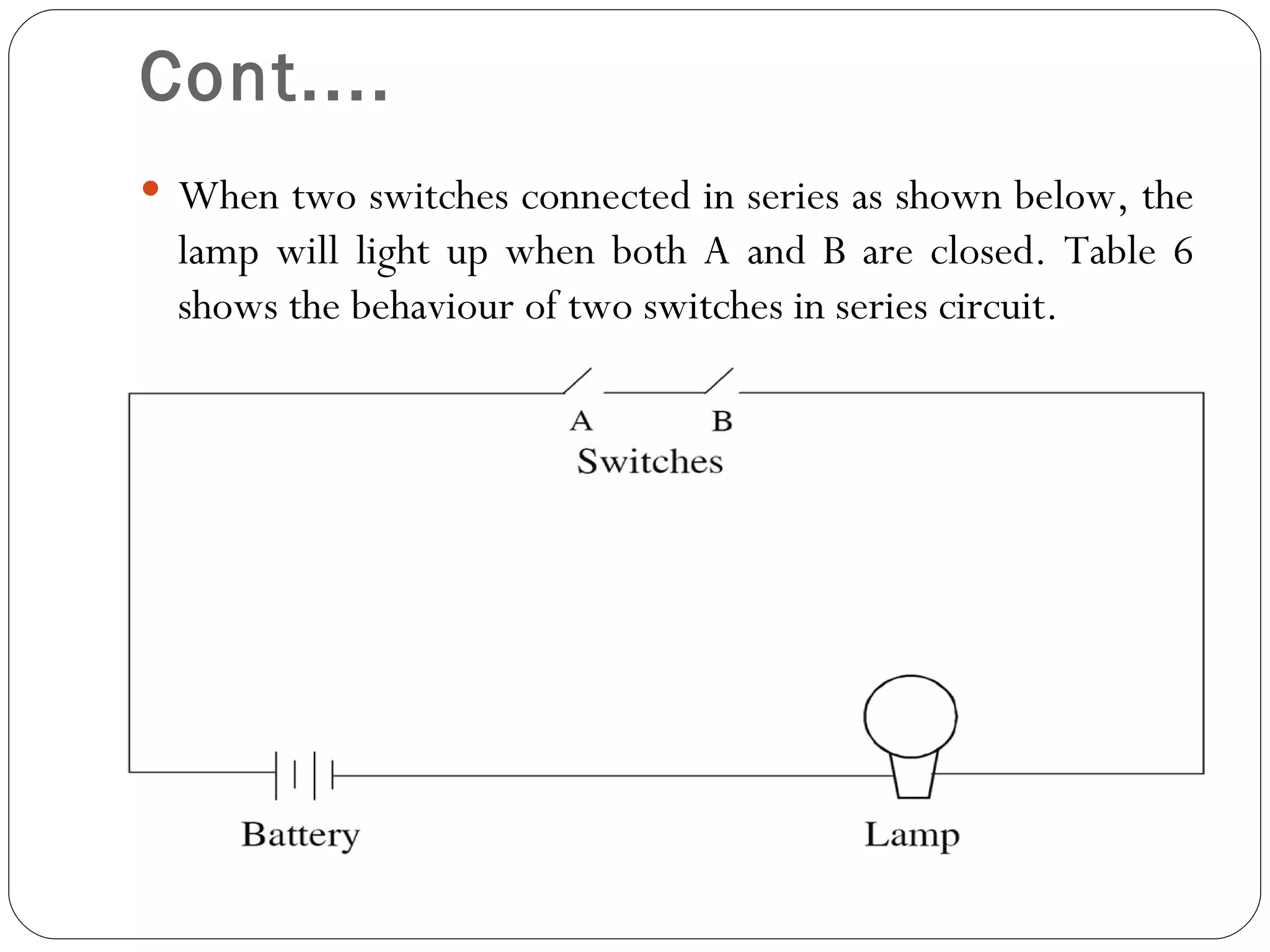
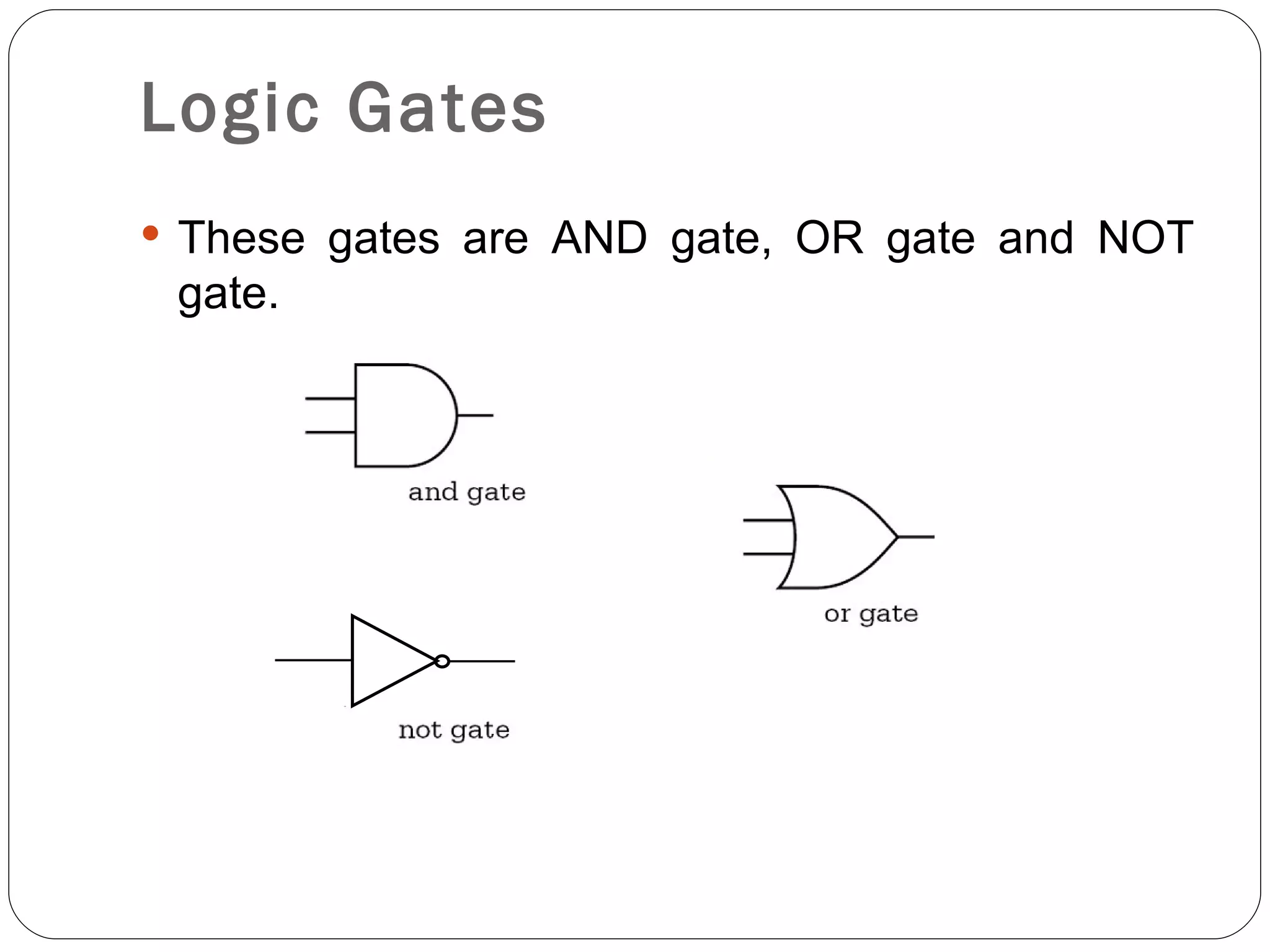
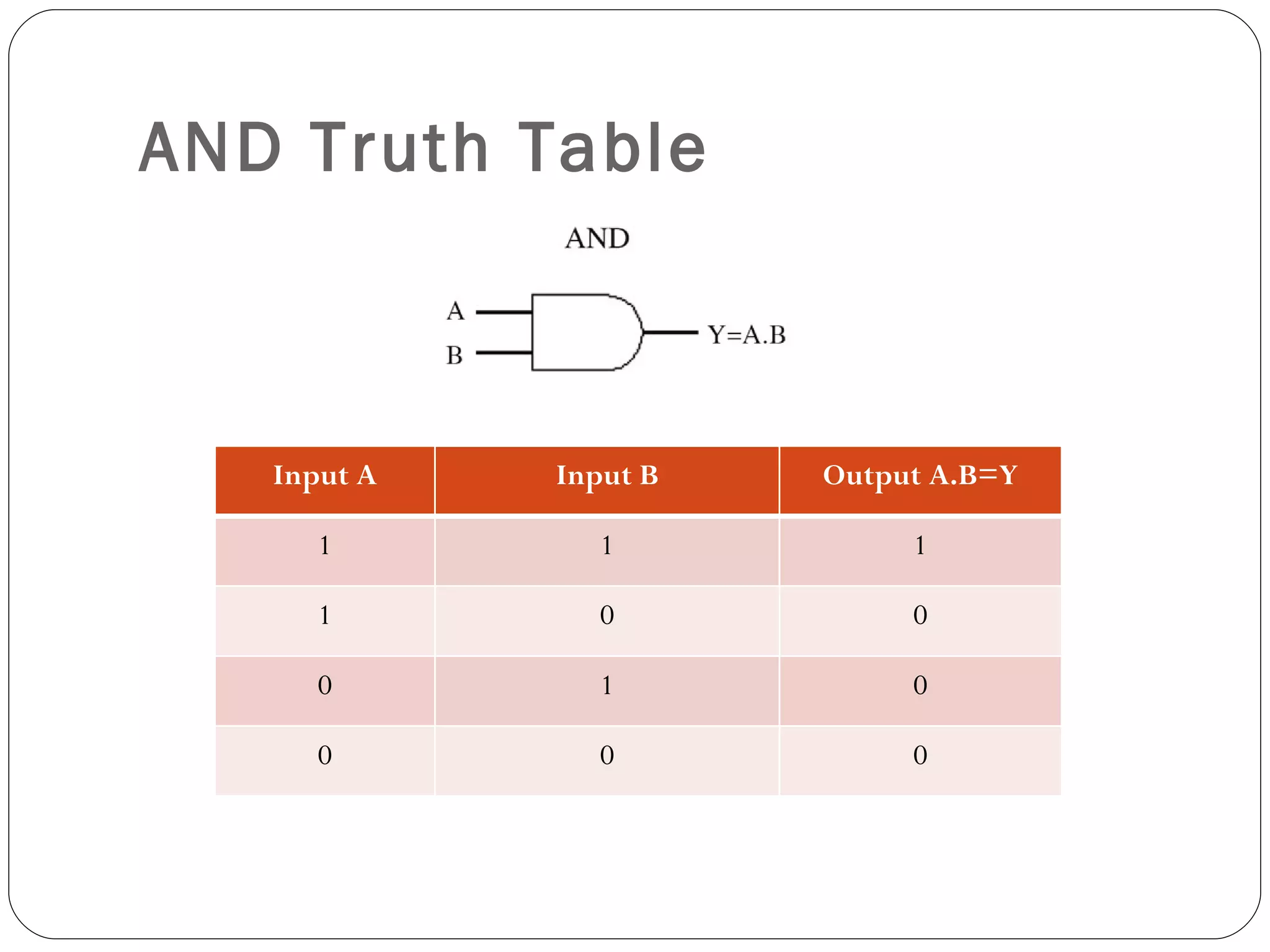
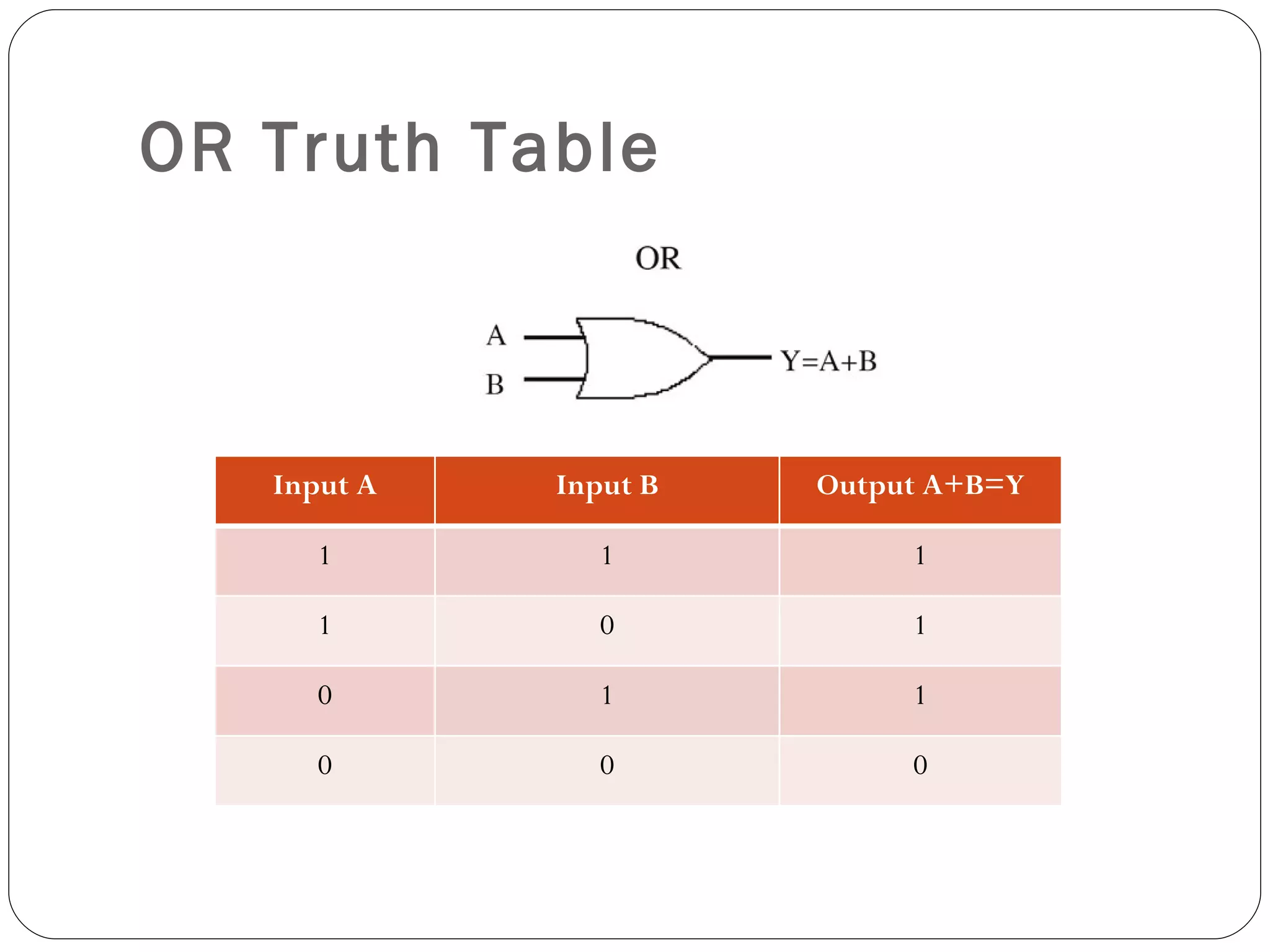
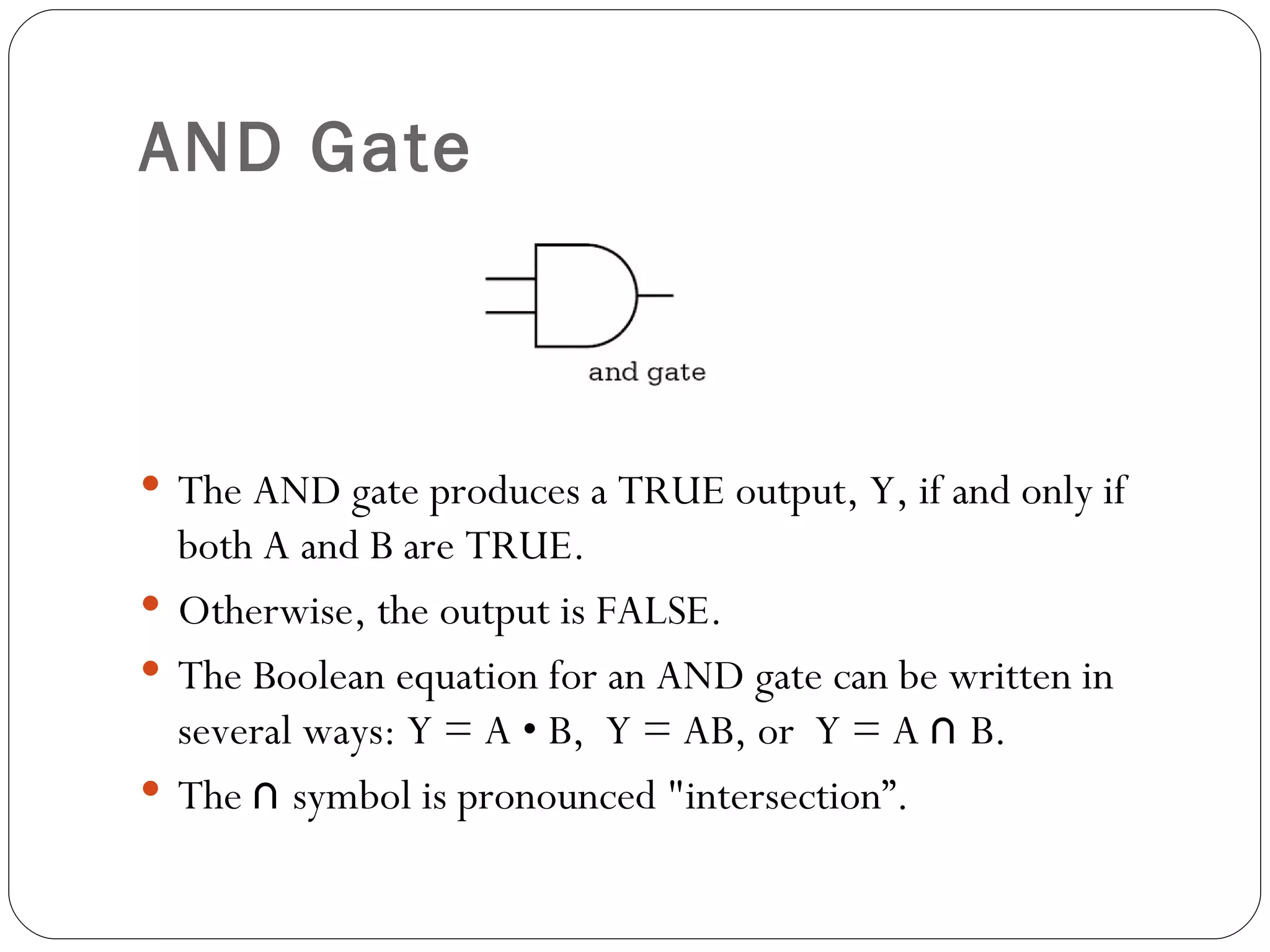
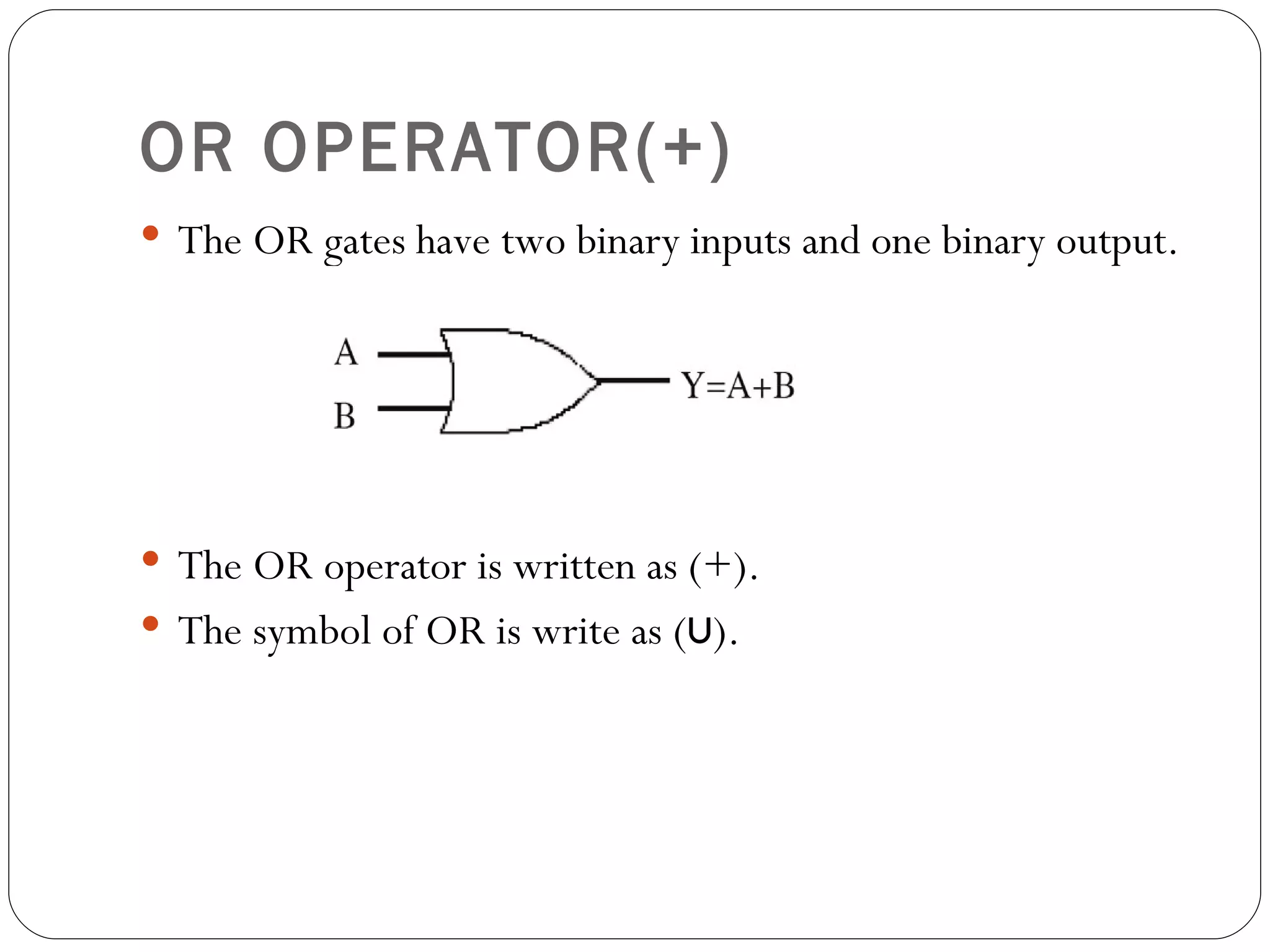
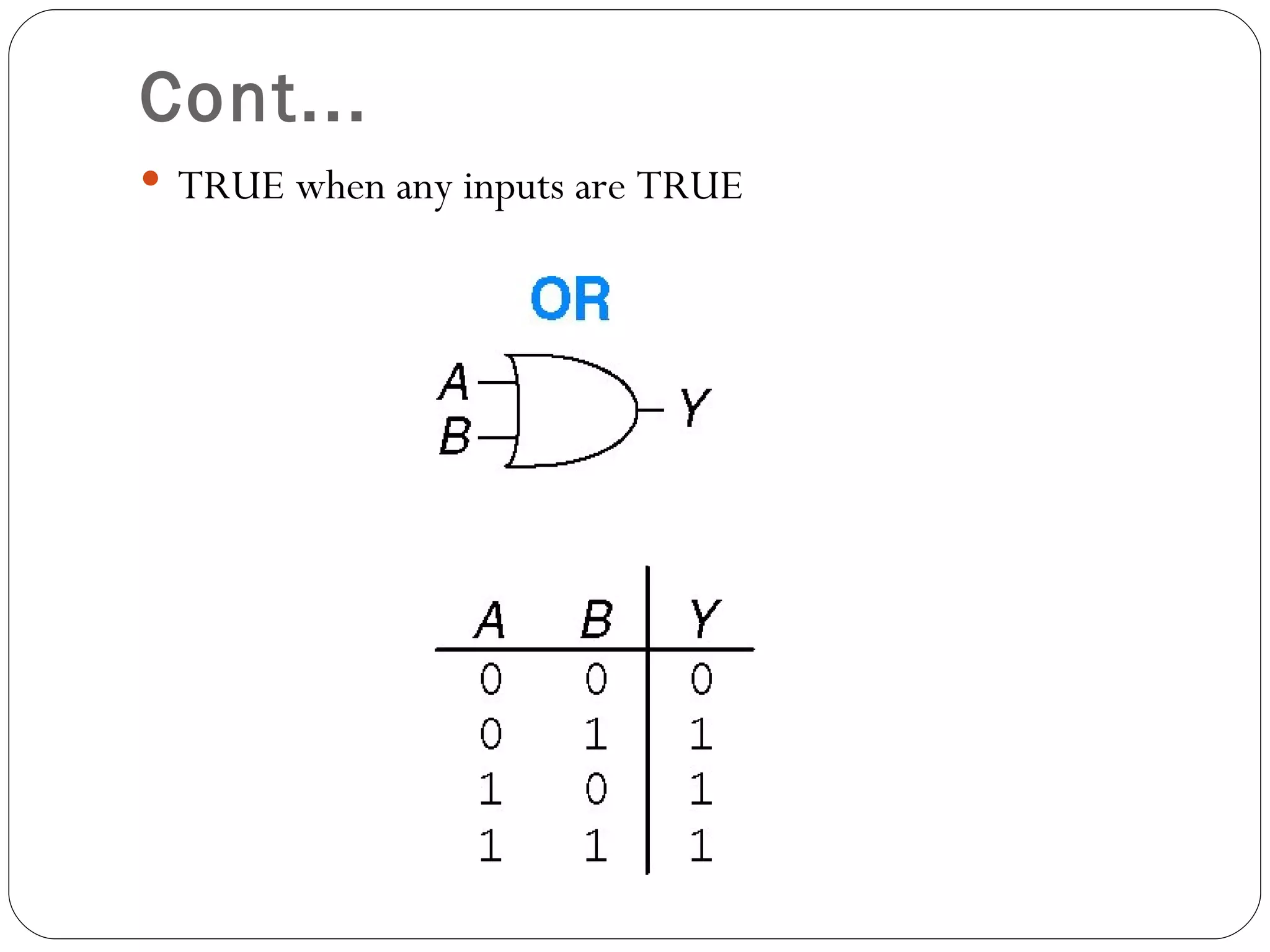
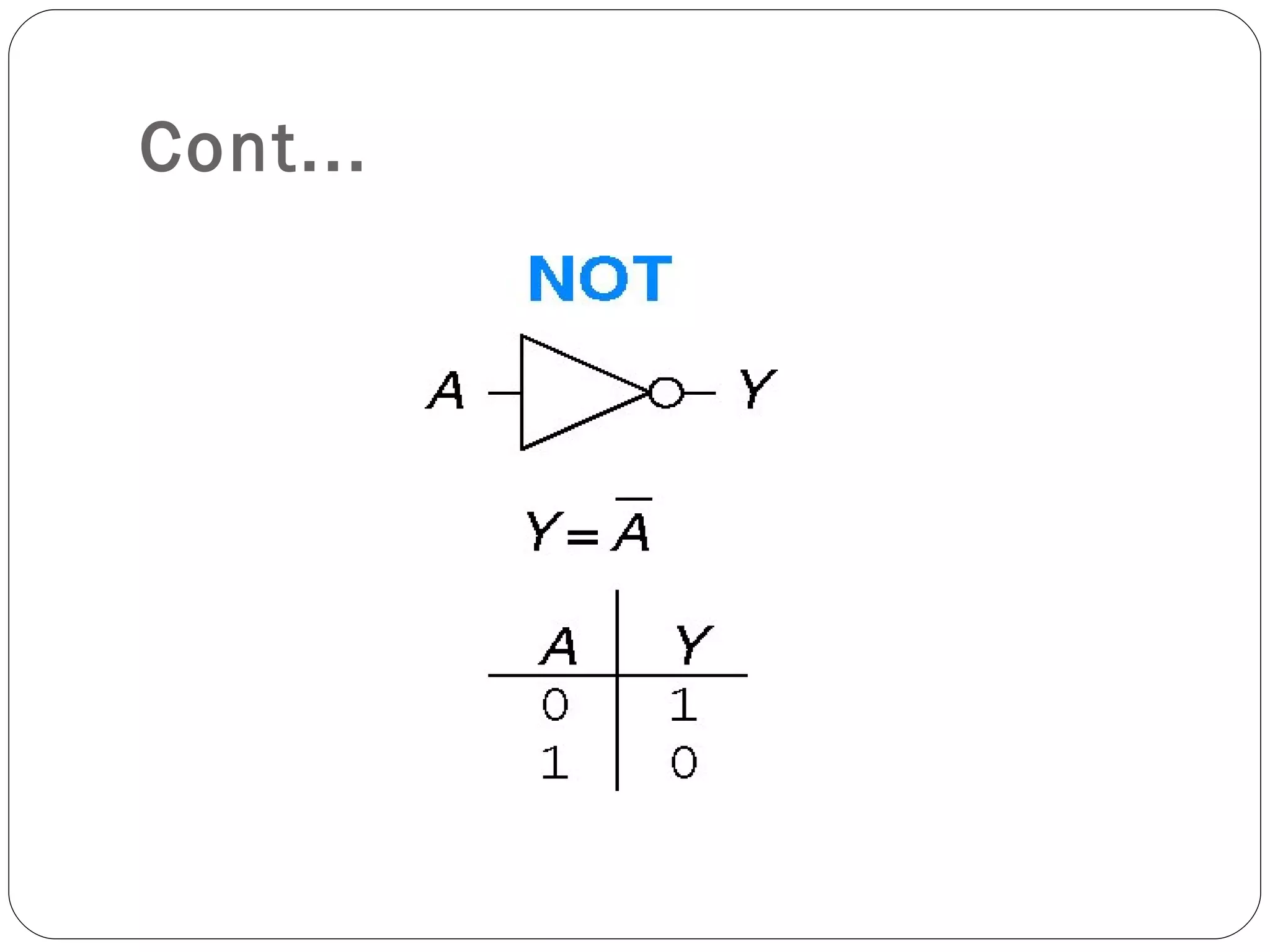
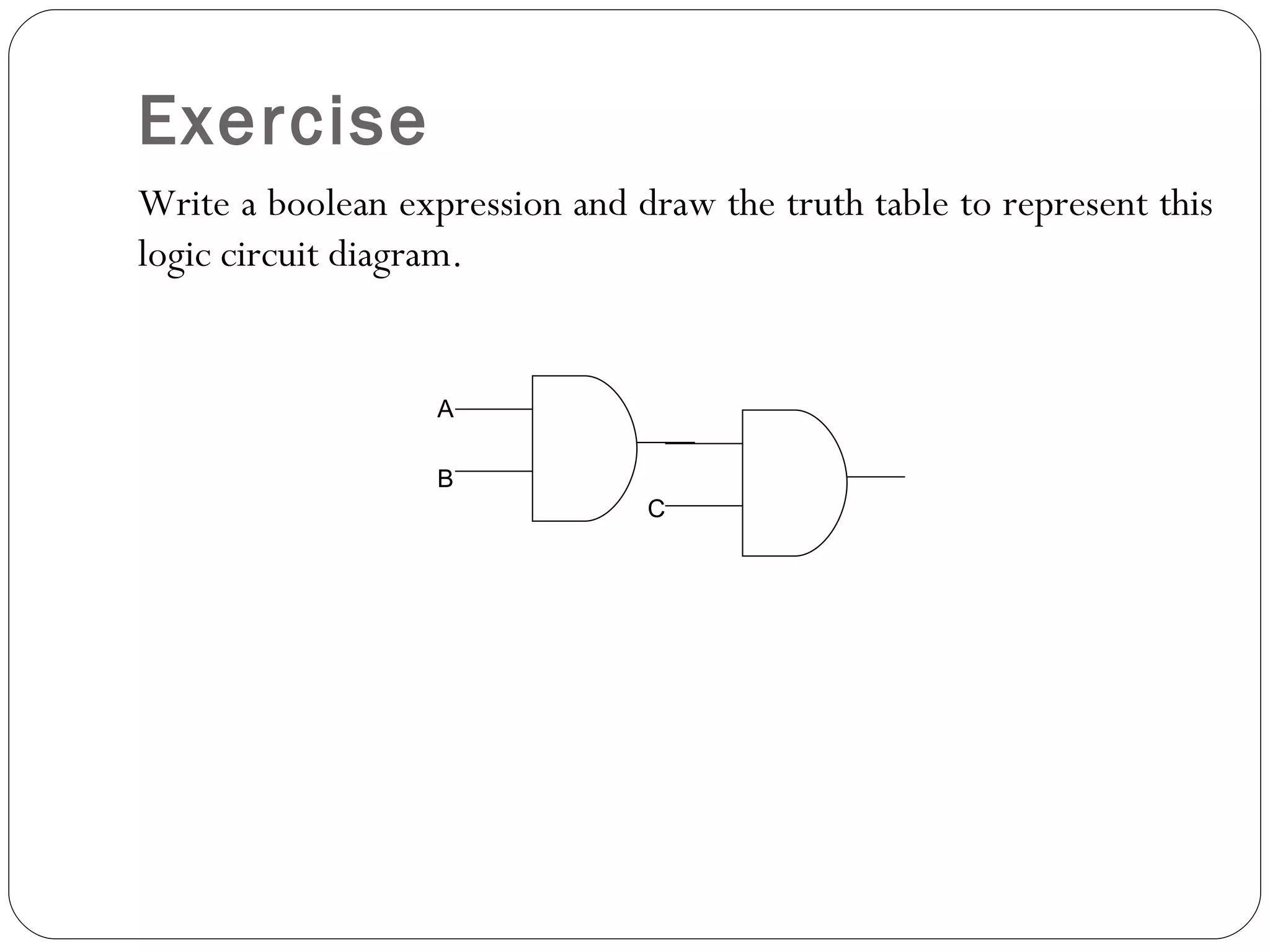
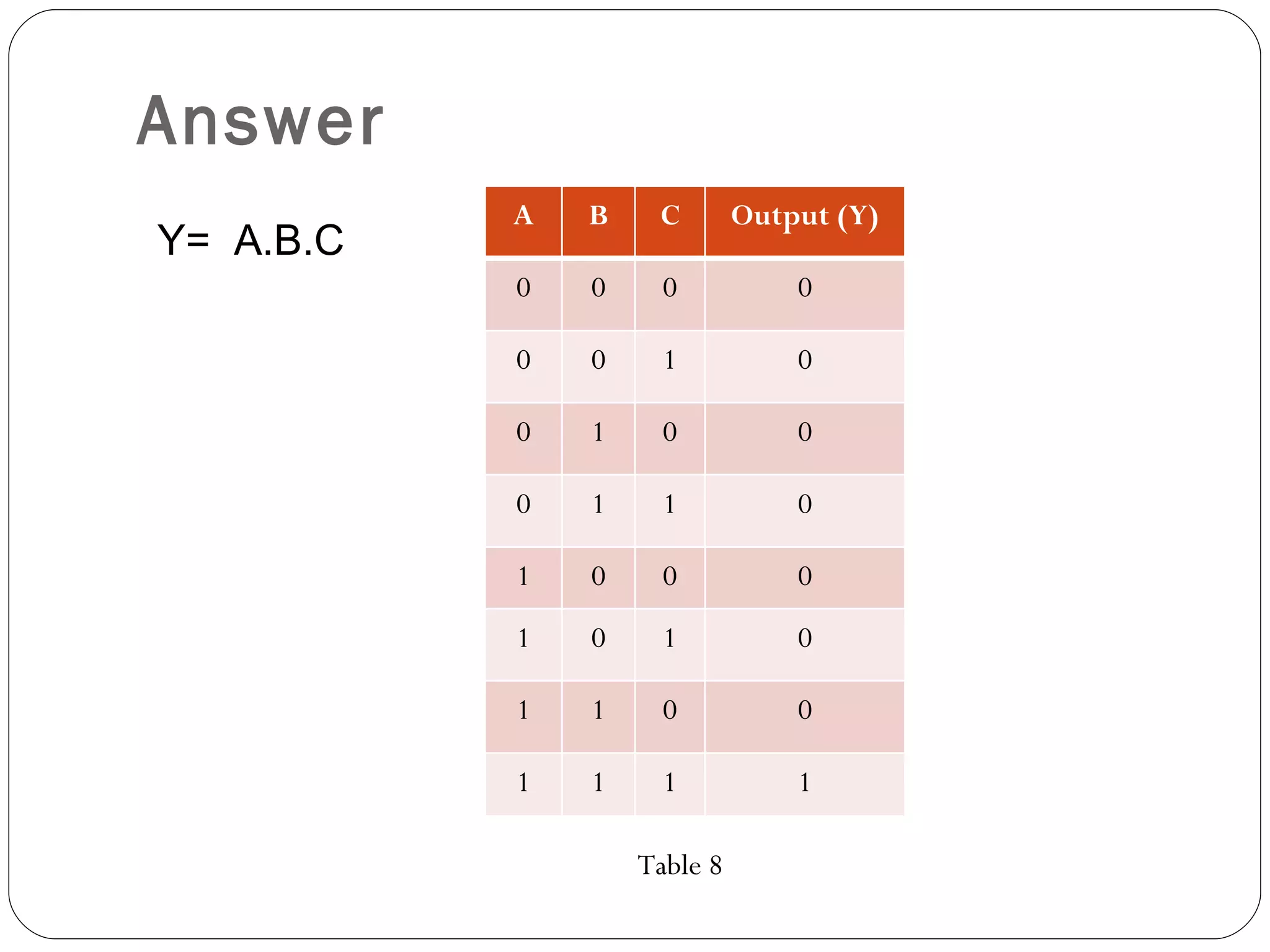
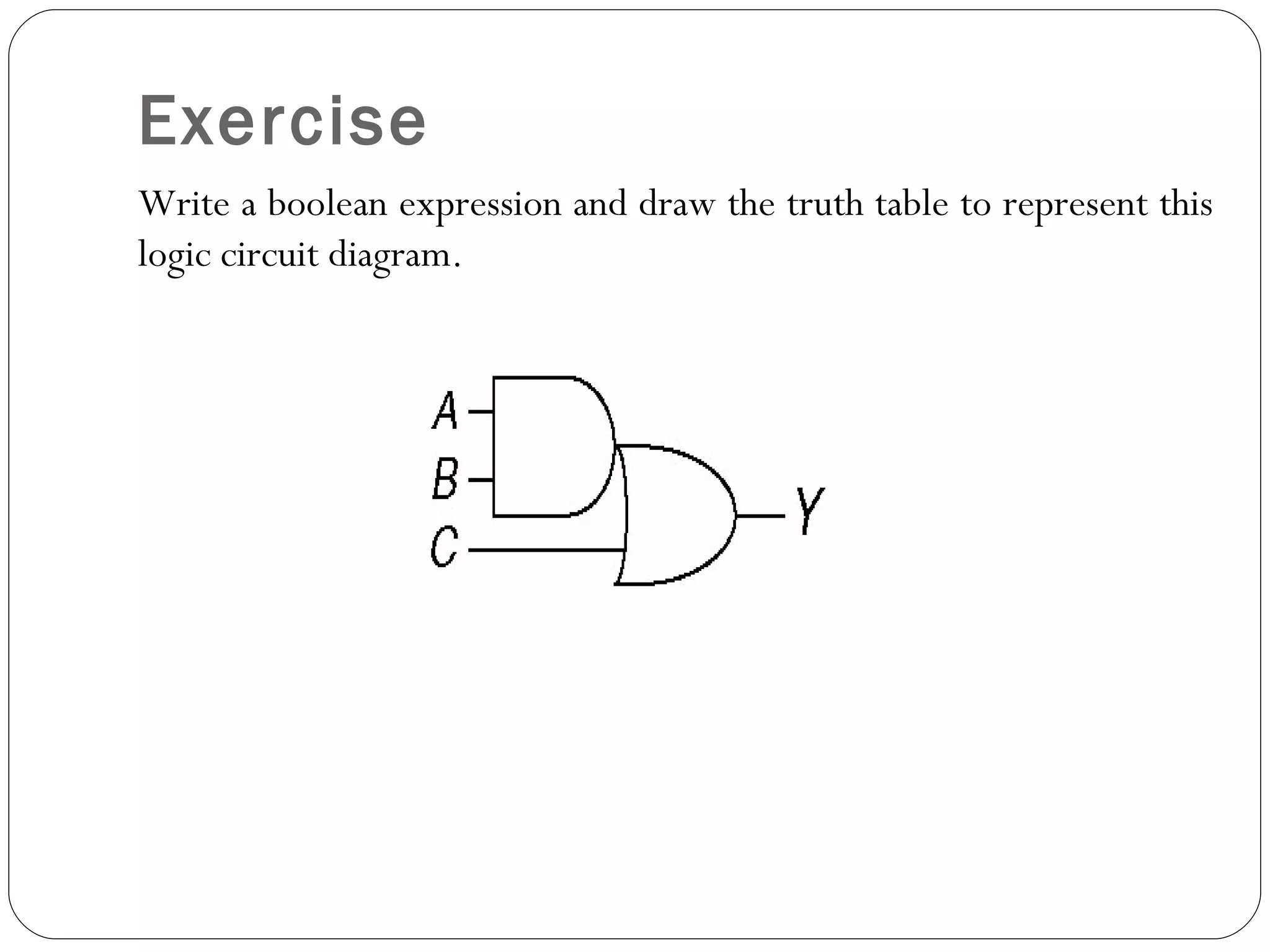
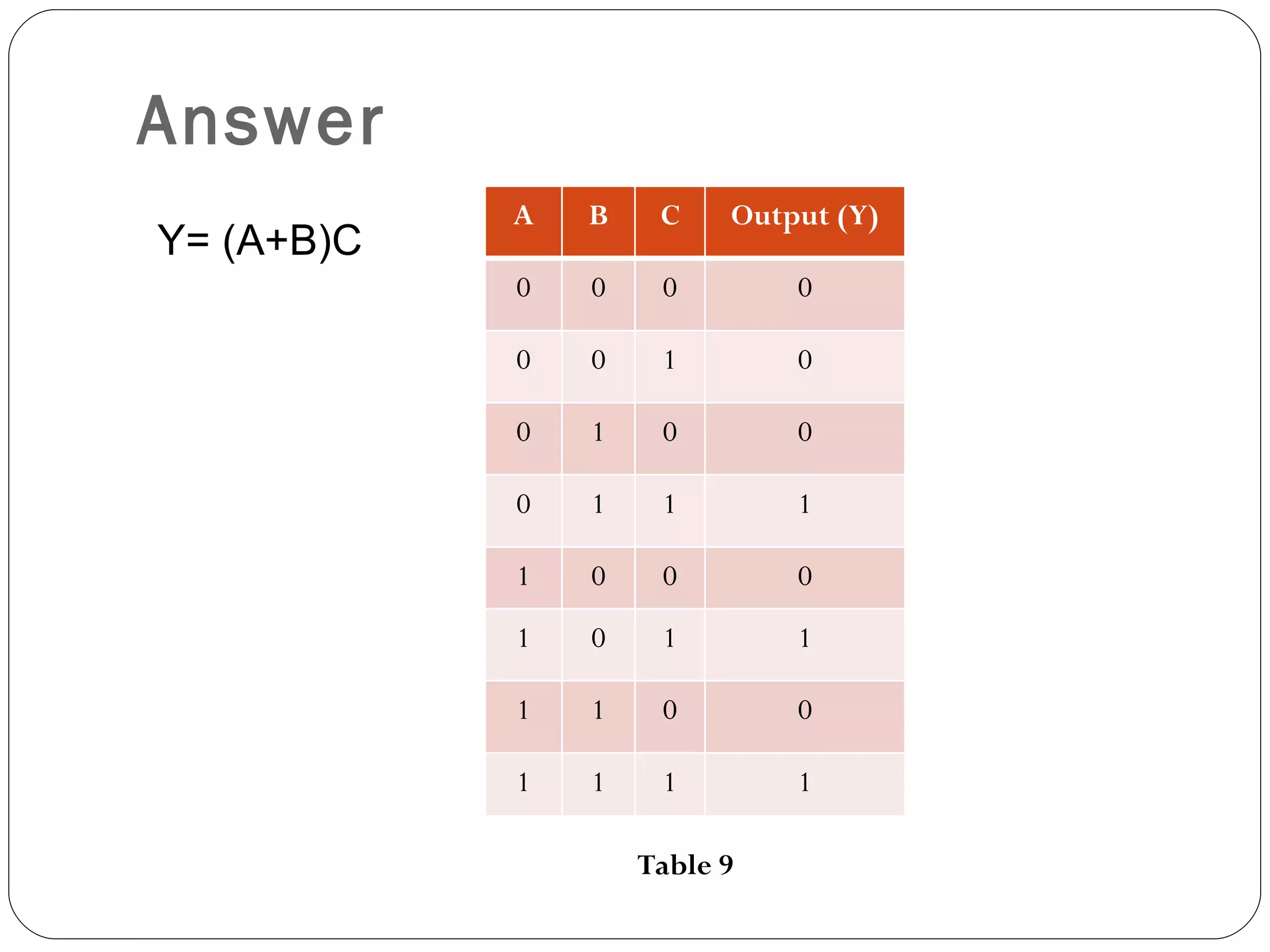
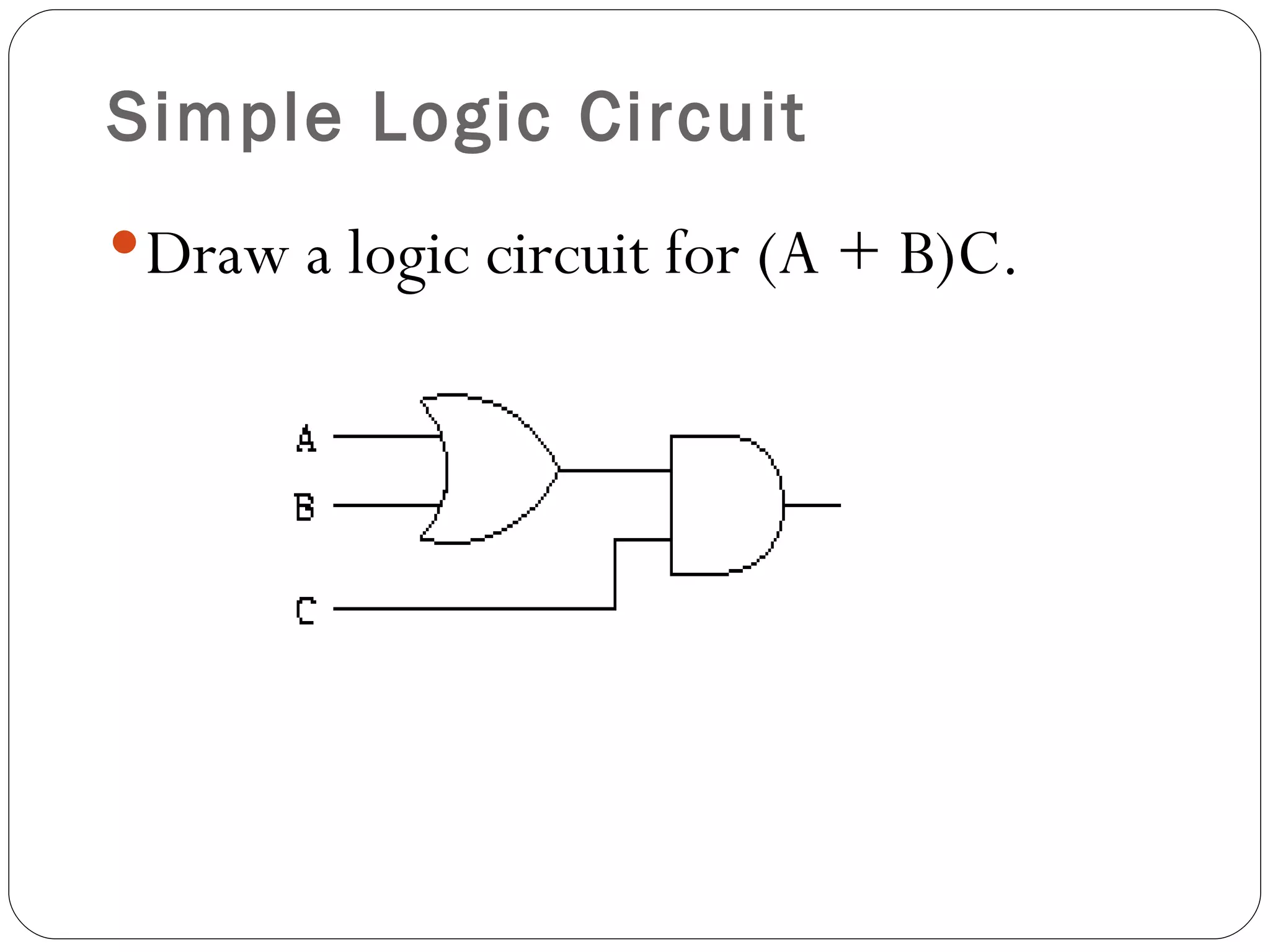
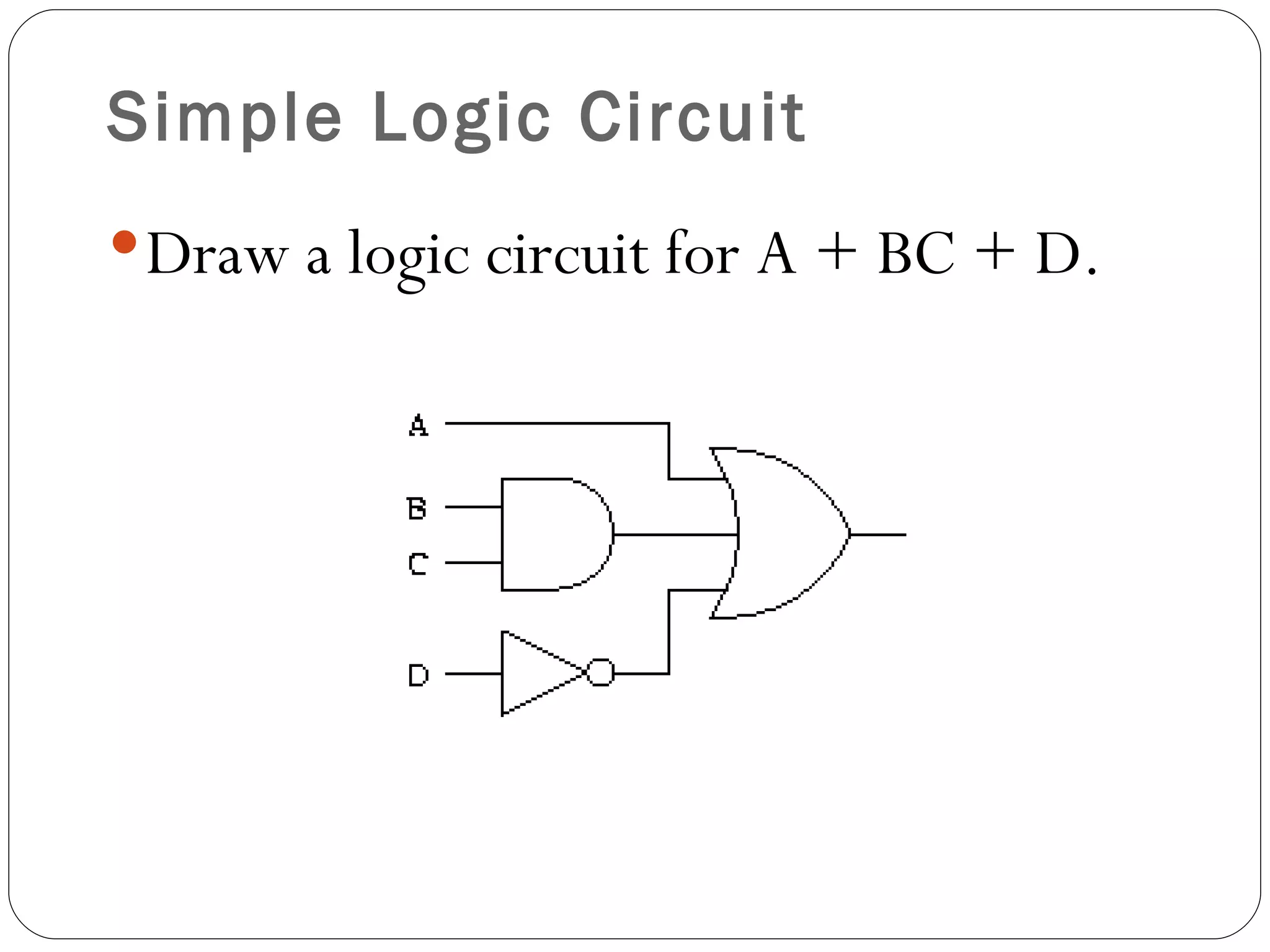
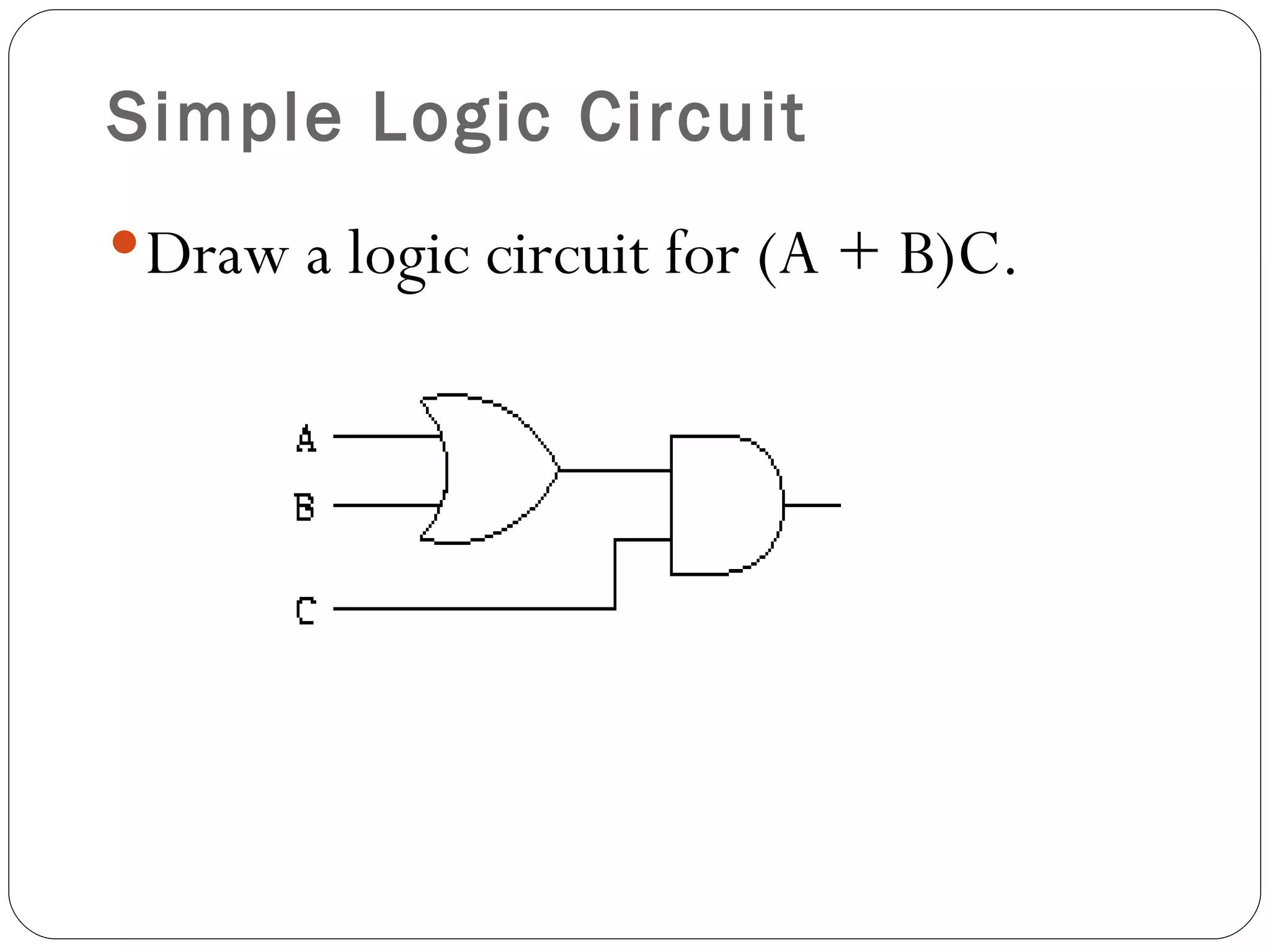
The document discusses Boolean expressions and logic gates. It begins by introducing Boolean algebra, including the axioms and theorems. It then explains logical addition (OR) and logical multiplication (AND) through truth tables. Complementation using NOT is also covered. Common logic gates - OR, AND, and NOT - are defined through their truth tables and symbols. Electrical switches are used as an example to illustrate Boolean logic. The document concludes by defining each type of logic gate in more detail.

1. 2.4.1 Boolean
Expression
Learning Outcome:
• Calculate the value of Boolean
Expression

2. Boolean Expression
 Introduction
 Axioms of Boolean Algebra
 Basic Theorems
 Logical Addition (OR Operation)
 Logical Multiplication (AND Operation)
 Complementation

3. Introduction
 The basic rules for simplifying and combining logic
gates are called Boolean algebra in honour of
George Boole (1815-1864).
 There are two types of operator:
Unary – NOT
Binary – AND, OR

4. Axioms of Boolean Algebra
 For any elements a, b and c of the set B on which two binary
operations (+ , .) and a unary operation denoted (-) or (~) or (ù)
are defined (OR, AND, NOT respectively), and 0 and 1 denote
two distinct elements of B. Then
 Commutative Laws
a+b=b+a
a.b=b.a
 Distributive Laws
 a + (b . c) = (a + b) . (a + c)
 a . (b + c) = (a . b) + (a . c)
 Identity Laws
a+0=a
a.1=a
 Complement Laws
a+~a=1
a.~a=0

5. Basic Theorems
 Let a, b, c be any three elements in a Boolean algebra B. Then
 Idempotent Laws
 a+a=a
 a.a=a
 Boundedness Laws
 a+1=1
 a.0=0
 Absorption Laws
 a + (a . b) = a
 a . (a + b) = a
 Associative Laws
 (a + b ) + c = a + (b + c)
 (a . b) . c = a . (b . c)
 (Uniqueness of Complement)
 If a + x = 1 and a . x = 0, then x = ~ a
 ~0=1~1=0
 De Morgan’s Laws:

6. Logical Addition (OR
Operation)
 Each variable in Boolean algebra has either of two values:
true or false (l or 0).
 For instance, in logic equation, A + B = C, each of the
variables A, B and C may have only the values 0 or 1.
 We can define the “+” symbol by listing all possible
combinations for A and B and the resulting values of A + B.

7. Cont...
Input Output
A B C = A+B
0 0 0
1 0 1
0 1 1
1 1 1
Table 2

8. Cont...
 Above table is a truth table of logical addition and could
represent binary addition table except for the last entry.
 The + symbol, therefore, does not have the normal meaning
of arithmetic addition but is a logical addition and is referred
as OR operation.
 The equation A + B = C can be read as A OR B equals C.
This concept can be extended to any number of variables.
 To avoid ambiguity, a number of other symbols have been
recommended as replacements for the + sign, for example,
U and therefore A + B = C can be written as A ∪ B = C.

9. Logical Multiplication (AND
Operation)
 A second important operation in Boolean algebra is logical
multiplication and is referred to as AND operation.
 The logical multiplication of two variables A and B is expressed as
A.B and is read as A AND B. The Boolean equation for an AND
gate can be written in as Y = A • B, Y = AB, or Y = A ∩ B.
 The truth table for logical multiplication of two variables is,
Input Output
A B C=A*B
0 0 0
1 0 0
0 1 0
1 1 1
Table 3

10. Complementation
 Boolean algebra uses an operation called complementation
and this can be defined as ~0 = 1 and ~1 = 0.
 ~A means the complement of A and read as NOT A. The
process of complementing is called negation,
Input Output
A B=~A
0 1
1 0
Table 4

11. Exercise 1
Evaluate the following Boolean expressions:
l 1+1+1
l 1+1+0
l 1.1.1
l 1.1.0
Answer.
i) 1 + 1 + 1 = (1 + 1) + 1 = 1 + 1 = 1
j) 1 + 1 + 0 = (1 + 1) + 0 = 1 + 0 = 1
k) 1.1.1 = (1.1). 1 = 1.1 = 1
l) 1.1.0 = (1.1). 0 = 1.0 = 0

12. Exercise 2
Evaluate the following.
l 1. (1 + 0)
l (1 + 1). (1 + 0)
l (1.1) + (0.1)
Answer.
 As in ordinary arithmetic, Operations in parenthesis are done
first.
i) 1. (1 + 0) = 1.1 = 1
j) (1+1). (1+0) = 1.1 = 1
k) (1.1) + (0.1) = 1 + 0 = 1

13. Exercise 3
Evaluate 1.1 + 0.1
Answer.
 In ordinary arithmetic, multiplication takes precedence over
addition. The Boolean AND takes precedence over the
Boolean OR.
 1.1 + 0.1 = 1 + 0 = 1
 This example illustrates that (1.1) + (0.1) is the same as 1.1
+ 0.1. The brackets are not needed. This is similar to (5 * 2)
+ (3 * 4) = 5 * 2 + 3 * 4. The brackets are not needed.

14. Exercise 4
In ordinary mathematics we say that multiplication distributes over
addition. For (4) 2(a + b) = 2a + 2b
Does the AND operation distribute over the OR operation? For
example, is 1. (1 + 0) = 1.1 + 1.0?
Answer.
 Left Side: 1. (1 + 0) = 1.1 = 1
 Right Side: 1.1 + 1.0 = 1 + 0 = 1
 Left side = Right side
 Hence, AND does distribute over OR
 It should be noted that distributive Law of AND over OR does
hold in general in Boolean arithmetic.

15. 2.4.2 Logic Gates
Learning Outcome:
 Identify symbol for logic gate

16. 2.4.2 Logic Gates
 An electronic circuit operates on one or more
input signals to produce an output signal.
 Gates are digital (two-state) circuits and can be
analyzed with Boolean algebra.
 The circuit which performs OR operation is called
OR gate
 The circuit which performs AND operation is
called AND gate.

17. ELECTRICAL
SWITCHES
 Electrical switches are good examples to illustrate OR, AND
and many Boolean theorems.

18. Cont....
 A switch has only two states: either closed or open. When the
two switches are connected in parallel, the current will flow in
the circuit when either switch is in closed position.
 The current will not flow at all when both switches are in open
position.
 If the flowing current is taken as ON and not flowing as OFF,
and assumed that closed = 1, open = 0, ON = 1 and OFF = 0,
then behaviour of two switches can be tabulated as shown
below.
 This is precisely the property described by the truth table for
logical addition (OR operation).

19. Behaviour of two switches in
parallel
Switch A Switch B Bulb C
Open (0) Open (0) OFF (0)
Closed (1) Open (0) ON (1)
Open (0) Closed (1) ON (1)
Closed (1) Closed (1) ON (1)
Table 5

20. Cont....
 When two switches connected in series as shown below, the
lamp will light up when both A and B are closed. Table 6
shows the behaviour of two switches in series circuit.

21. Behaviour of Two Switches in
Series
Switch A Switch B Bulb C
Open (0) Open (0) OFF (0)
Closed (1) Open (0) OFF (0)
Open (0) Closed (1) OFF (0)
Closed (1) Closed (1) ON (1)
Table 6

22. Logic Gates
 These gates are AND gate, OR gate and NOT
gate.

23. Cont...
 A gate will have one or more binary
inputs of 0 or 1 but just one binary
output.
a) The AND and OR gates each have two binary
inputs and one binary output.
b) The NOT gate has one binary input and one
binary output.

24. Truth Table
 A truth table is a good way to show the function
of a logic gate.
 It shows the output states for every possible
combination of input states.
 The symbols 0 (false) and 1 (true) are used in
truth tables
 For a logic gate with n inputs, there are 2n entries
in the truth table.
 Example: A logic gate with three inputs, A, B and
C will contain 23 = 8 entries.

25. AND Truth Table
Input A Input B Output A.B=Y
1 1 1
1 0 0
0 1 0
0 0 0

26. OR Truth Table
Input A Input B Output A+B=Y
1 1 1
1 0 1
0 1 1
0 0 0

27. NOT Truth Table
Input A Output A’=Y
0 1
1 0

28. THE AND OPERATOR (.)
 The AND gates have two binary inputs and one binary
output.
 The AND operator is written as (.).
 The symbol of AND is written as (∩).

29. AND Truth Table

30. AND Gate
 The AND gate produces a TRUE output, Y, if and only if
both A and B are TRUE.
 Otherwise, the output is FALSE.
 The Boolean equation for an AND gate can be written in
several ways: Y = A • B, Y = AB, or Y = A ∩ B.
 The ∩ symbol is pronounced "intersection”.

31. Cont...
 TRUE when all inputs are TRUE

32. OR OPERATOR(+)
 The OR gates have two binary inputs and one binary output.
 The OR operator is written as (+).
 The symbol of OR is write as (∪).

33. OR Truth Table

34. OR Gate
 The OR gate produces a TRUE output, Y if either A or B (or
both) are TRUE.
 The Boolean equation for an OR gate is written as Y = A +
B or Y = A ∪ B.
 The ∪ symbol is pronounced “union”.
 TRUE when any inputs are TRUE

35. Cont...
 TRUE when any inputs are TRUE

36. NOT OPERATOR (~)
 The NOT gate has one binary input and one binary
output.
 The NOT A can be written as below:
(~A), ( ), (¬A), (A’), (!A ).

37. NOT Gate
 The NOT gate's output is the inverse of its input. If A is
FALSE, then Y is TRUE. If A is TRUE, then Y is FALSE.
 This relationship is summarized by the truth table and
Boolean equation.
 The line over A in the Boolean equation is pronounced
NOT, so Y is read as “Y equals NOT A”.
 The NOT gate is also called an inverter.

38. NOT Truth Table
 ~0 = 1 is read as NOT 0 equals to 1. It is important to
remember that the NOT function inverts input.
 The NOT function takes an input of 0 and inverts it to
provide an output of 1 and it takes an input of 1 and inverts it
to provide an output of 0.

39. Cont...

40. Review Question
 Explain the following logic gates:
Operator Symbol Gate Input Gate, n Input Truth
Table (2n)
AND
OR
NOT
NAND
NOR

41.  Explain the following logic gates:
Operator Symbol Gate Input Gate, n Input Truth
Table (2n)
AND ., ∩ 2 4
OR +, ∪ 2 4
(~), ( ), (¬),
NOT 1 2
(’), (! ).
NAND 2 4
NOR 2 4
Table 7

42. Exercise
Write a boolean expression and draw the truth table to represent this
logic circuit diagram.
A
B
C

43. Answer
A B C Output (Y)
Y= A.B.C
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Table 8

44. Exercise
Write a boolean expression and draw the truth table to represent this
logic circuit diagram.

45. Answer
A B C Output
Y= (A.B) + C
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
Table 9

46. Exercise
Write a boolean expression and draw the truth table to represent this
logic circuit diagram.
A
B Y
C

47. Answer
A B C Output (Y)
Y= (A+B)C
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
Table 9

48. 2.4.3 Simple Logic
Circuit
Learning Outcome:
 Draw simple logic circuit from a
given boolean expression

49. Simple Logic Circuit
 Draw a logic circuit for (A + B)C.

50. Simple Logic Circuit
 Draw a logic circuit for A + BC + D.

51. Simple Logic Circuit
 Draw a logic circuit for (A + B)C.