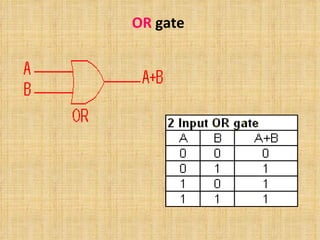
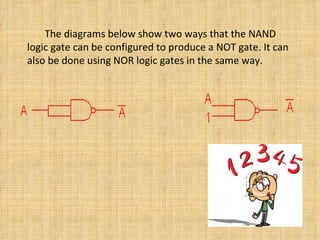
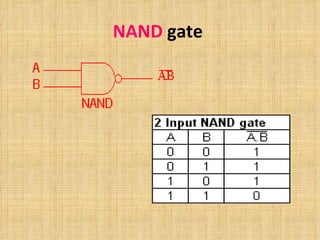
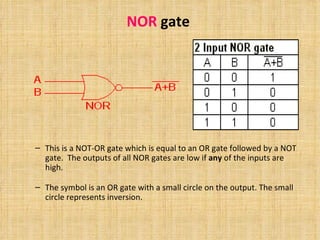
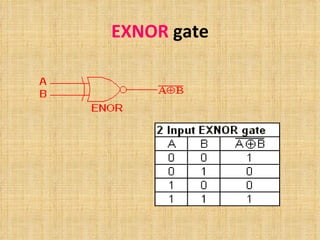
The document discusses Boolean algebra and logic gates. It defines Boolean algebra as a mathematical structure developed by George Boole to manipulate binary circuits algebraically. It focuses on three Boolean operations: complementation, sum (OR), and product (AND). It also defines basic logic gates like AND, OR, NOT, NAND, NOR, EXOR and EXNOR and how they can be used to represent Boolean functions.

1. By: Akash Chauhan

2. In the development of computer hardware, a decision was made to use binary circuits because it greatly simplified the electronic circuit design . In order to work with binary circuits, it is helpful to have a conceptual framework to manipulate the circuits algebraically, building only the final “most simple” result. George Boole (1813-1864) developed a mathematical structure to deal with binary operations with just two values. Today, we call these structures Boolean Algebras .

3. Boolean algebra provides the operations and the rules for working with the set {0, 1}. These are the rules that underlie electronic circuits , and the methods we will discuss are fundamental to VLSI design . We are going to focus on three operations : Boolean complementation, Boolean sum, and Boolean product

4. Boolean Operations The complement is denoted by a bar (on the slides, we will use a minus sign). It is defined by -0 = 1 and -1 = 0. The Boolean sum , denoted by + or by OR, has the following values: 1 + 1 = 1, 1 + 0 = 1, 0 + 1 = 1, 0 + 0 = 0 The Boolean product , denoted by  or by AND, has the following values: 1  1 = 1, 1  0 = 0, 0  1 = 0, 0  0 = 0

5. NOW WE ARE GOING TO FOCUS ON TOPICS Terminology AXIOMS LOGIC GATES

6. Terminology Element 0 is called “FALSE”. Element 1 is called “TRUE”. ‘ + ’ operation “ OR ”,‘ * ’ operation “ AND ” and ’ operation “ NOT ”. Juxtaposition implies * operation: ab = a * b Operator order of precedence is: ( ), ’, *, + . a+bc = a+(b*c) ≠ (a+b)*c ab’ = a(b’) ≠ (a*b)’ Single Bit Boolean Algebra( 1’ = 0 and 0’ = 1) + 0 1 0 0 1 1 1 1 * 0 1 0 0 0 1 0 1

7. Axiom A Boolean Algebra B is defined as a 5-tuple { B , + , * , ’ , 0 , 1 } + and * are binary operators,’ is a unary operator. The following axioms must hold for any elements a, b, c  {0,1}

8. Axiom #1: Closure If a and b are elements of B, (a + b) and (a * b) are in B. Axiom #2: Cardinality There are at least two elements a and b in B such that a != b. Axiom #3: Commutative If a and b are elements of B (a + b) = (b + a), and (a * b) = (b * a) Axiom #4: Associative If a and b are elements of B (a + b) + c = a + (b + c), and (a * b) * c = a * (b * c)

9. Axiom #5 : Identity Element B has identity elements with respect to + and * 0 is the identity element for +, and 1 is the identity element for * a + 0 = a and a * 1 = a Axiom #6: Distributive * is distributive over + and + is distributive over * a * (b + c) = (a * b) + (a * c), and a + (b * c) = (a + b) * (a + c) Axiom #7: Complement Element For every a in B there is an element a' in B such that a + a' = 1, and a * a' = 0

10. PRINCIPLE OF DUALITY changing each OR (+) sign to an AND (.) sign changing each AND (.) sign to an OR (+) sign. replacing each 0 by 1 & each 1 by 0 . e.g. 0+0 =1.1=1

11. Basic Gates and Functions Logic gates AND , OR , NOT , NAND , NOR , EXOR and EXNOR

12. AND gate

13. OR gate

14. NOT gate

15. The diagrams below show two ways that the NAND logic gate can be configured to produce a NOT gate . It can also be done using NOR logic gates in the same way .

16. NAND gate

17. NOR gate This is a NOT - OR gate which is equal to an OR gate followed by a NOT gate . The outputs of all NOR gates are low if any of the inputs are high . The symbol is an OR gate with a small circle on the output. The small circle represents inversion.

18. EXNOR gate

19. The NAND and NOR gates are called universal functions since with either one the AND and OR functions and NOT can be generated . Note : A function in sum of products form can be implemented using NAND gates by replacing all AND and OR gates by NAND gates . A function in product of sums form can be implemented using NOR gates by replacing all AND and OR gates by NOR gates . UNIVERSAL FUNCTIONS

20. Logic gates representation using the truth table TRUTH TABLE

21. THANK YOU