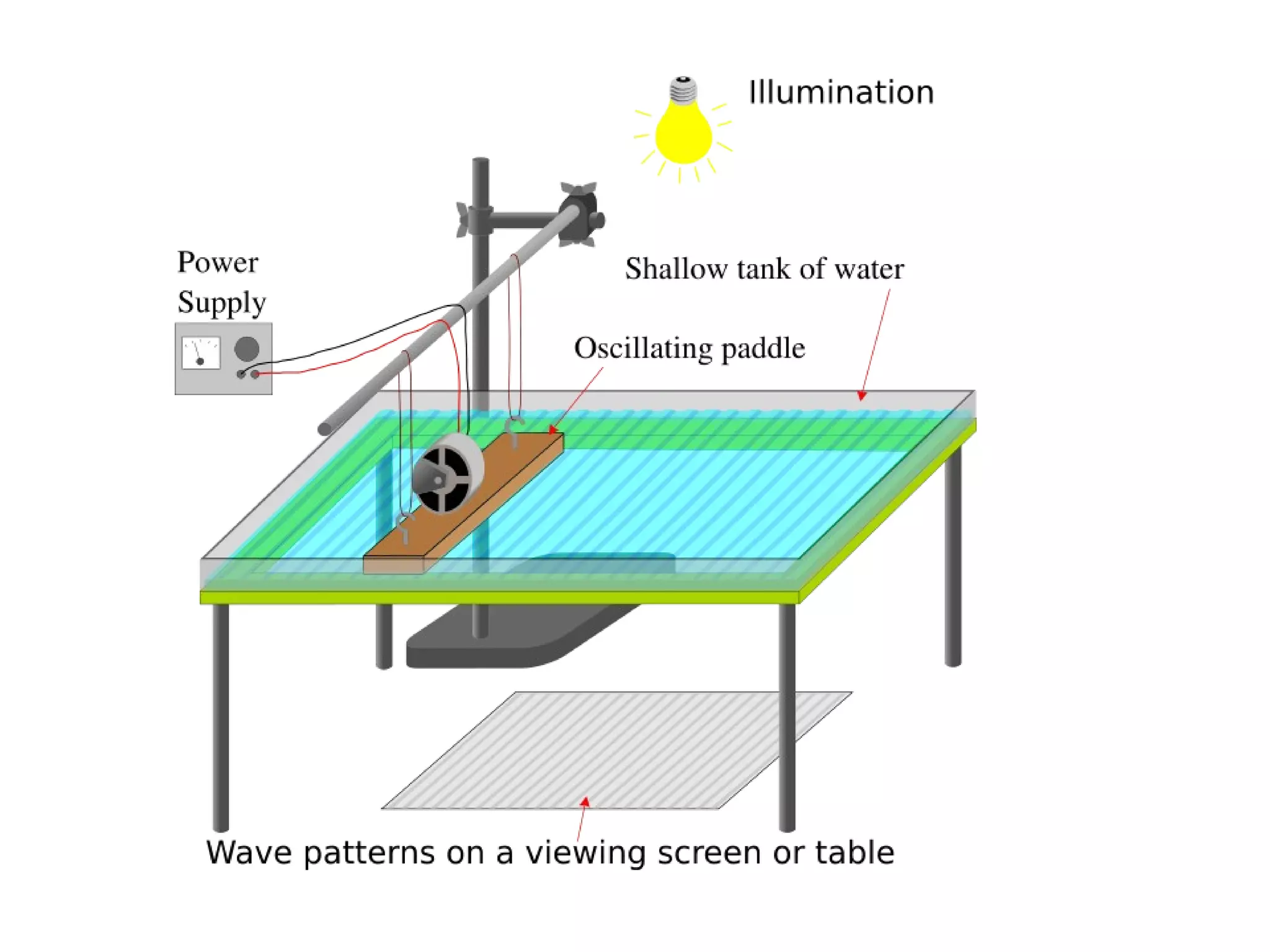
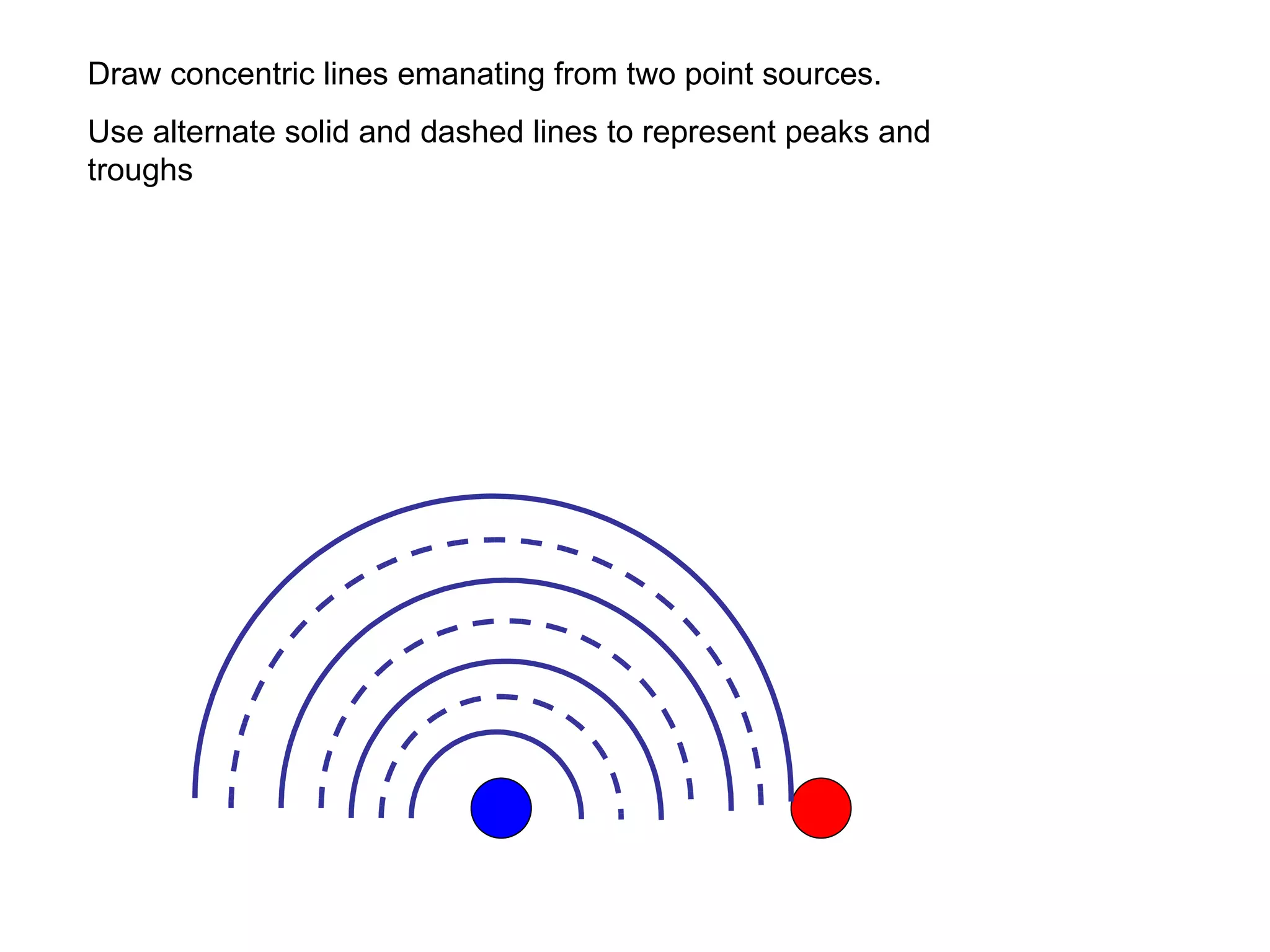
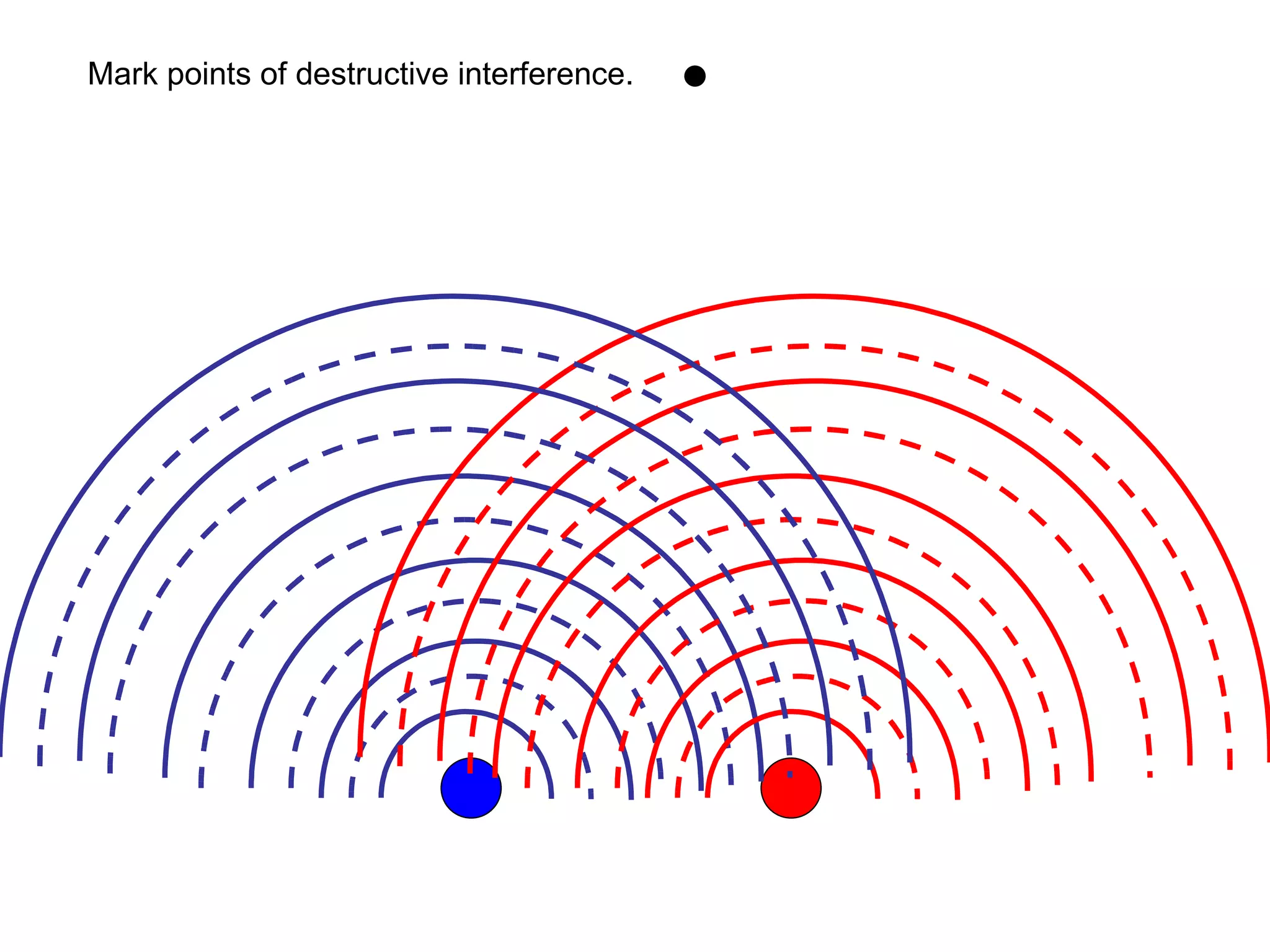
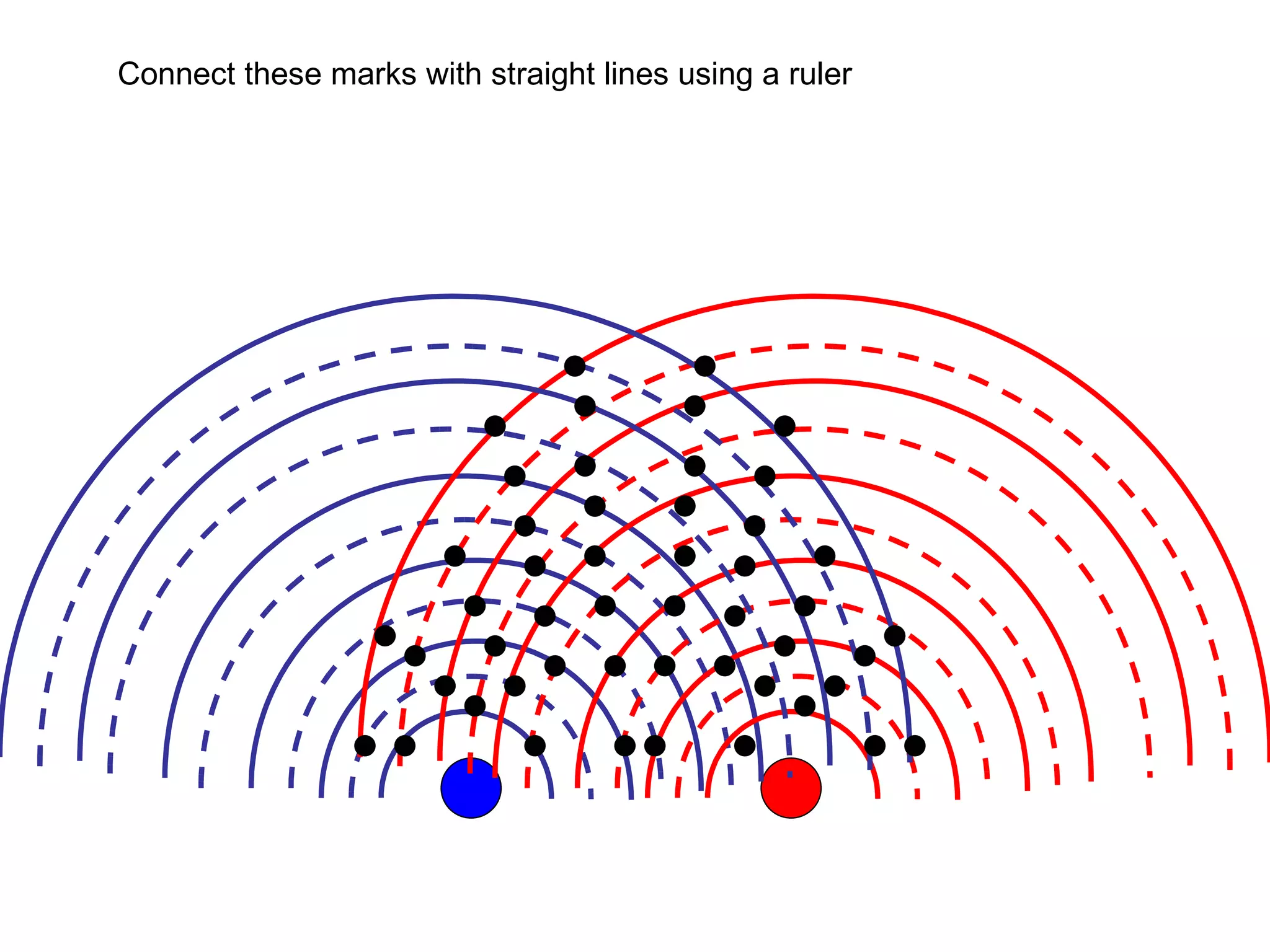
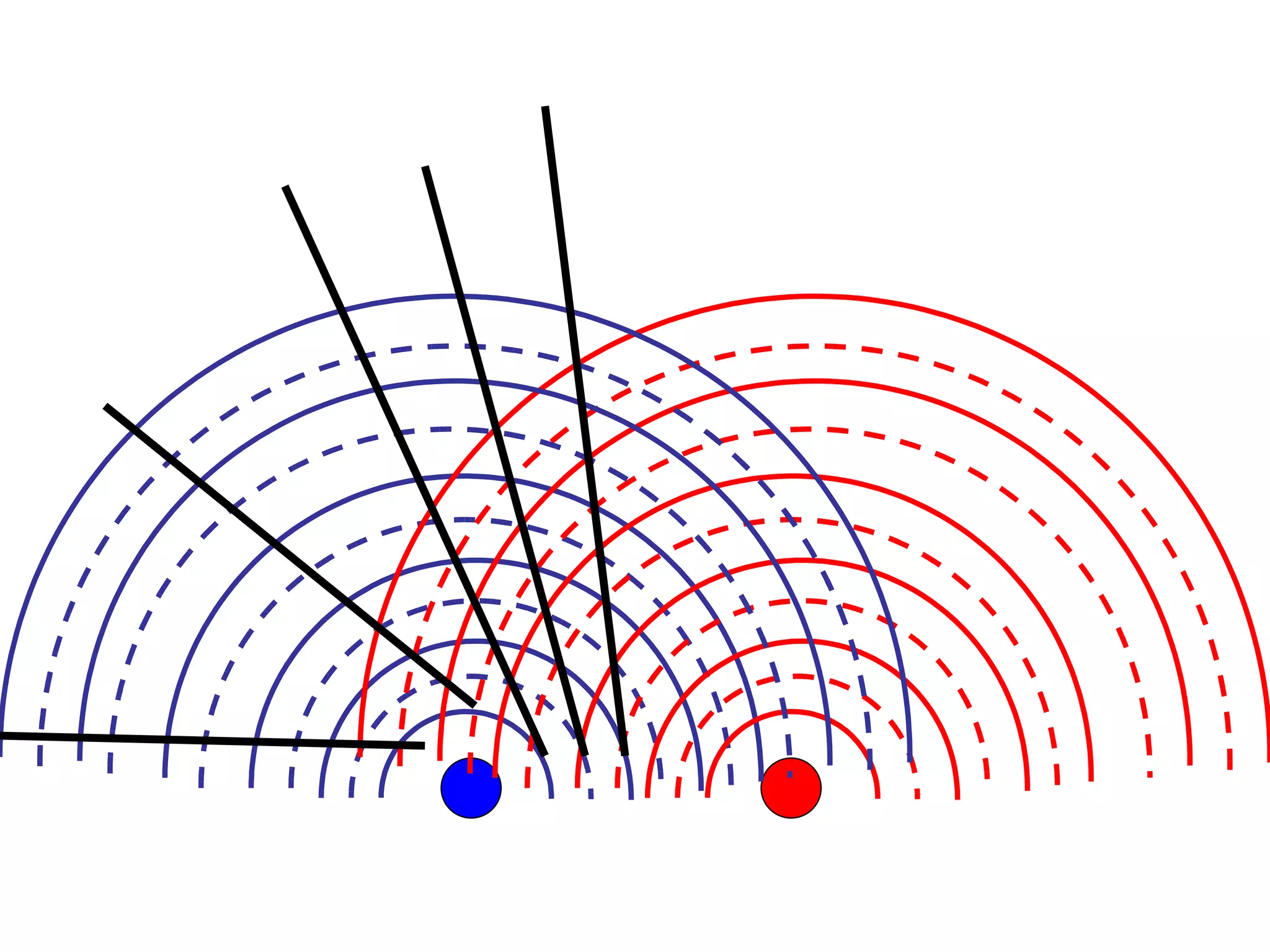
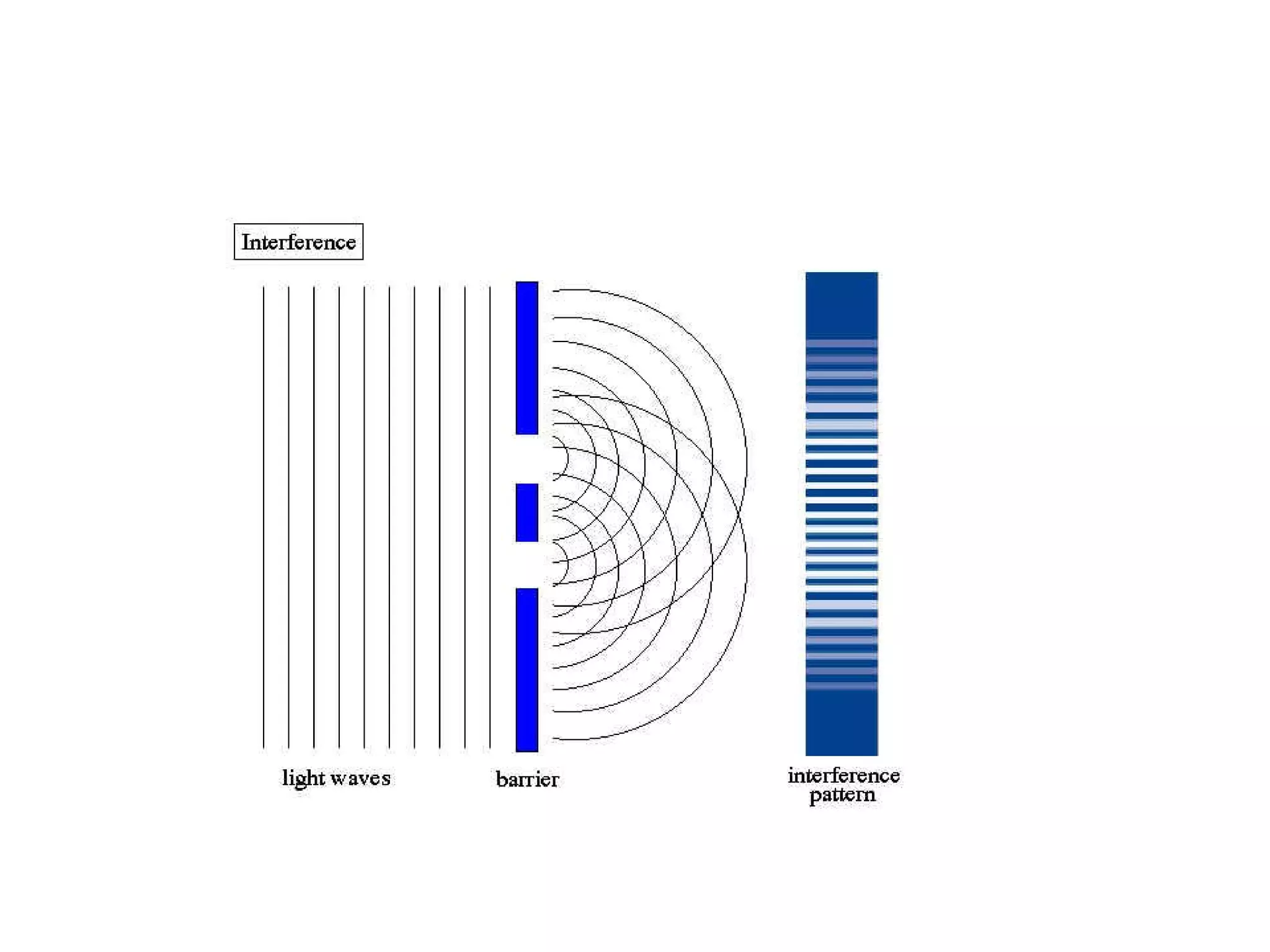
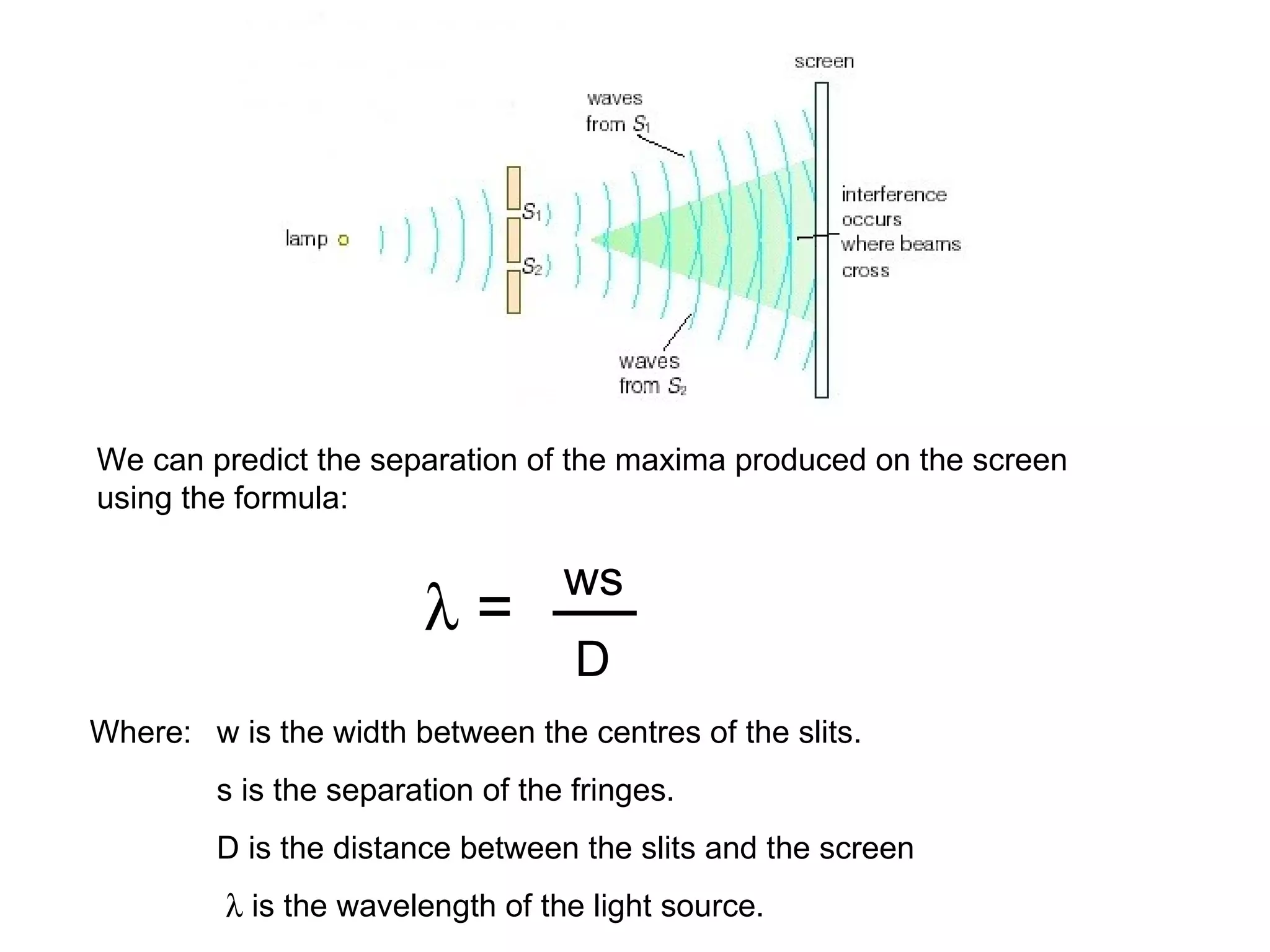
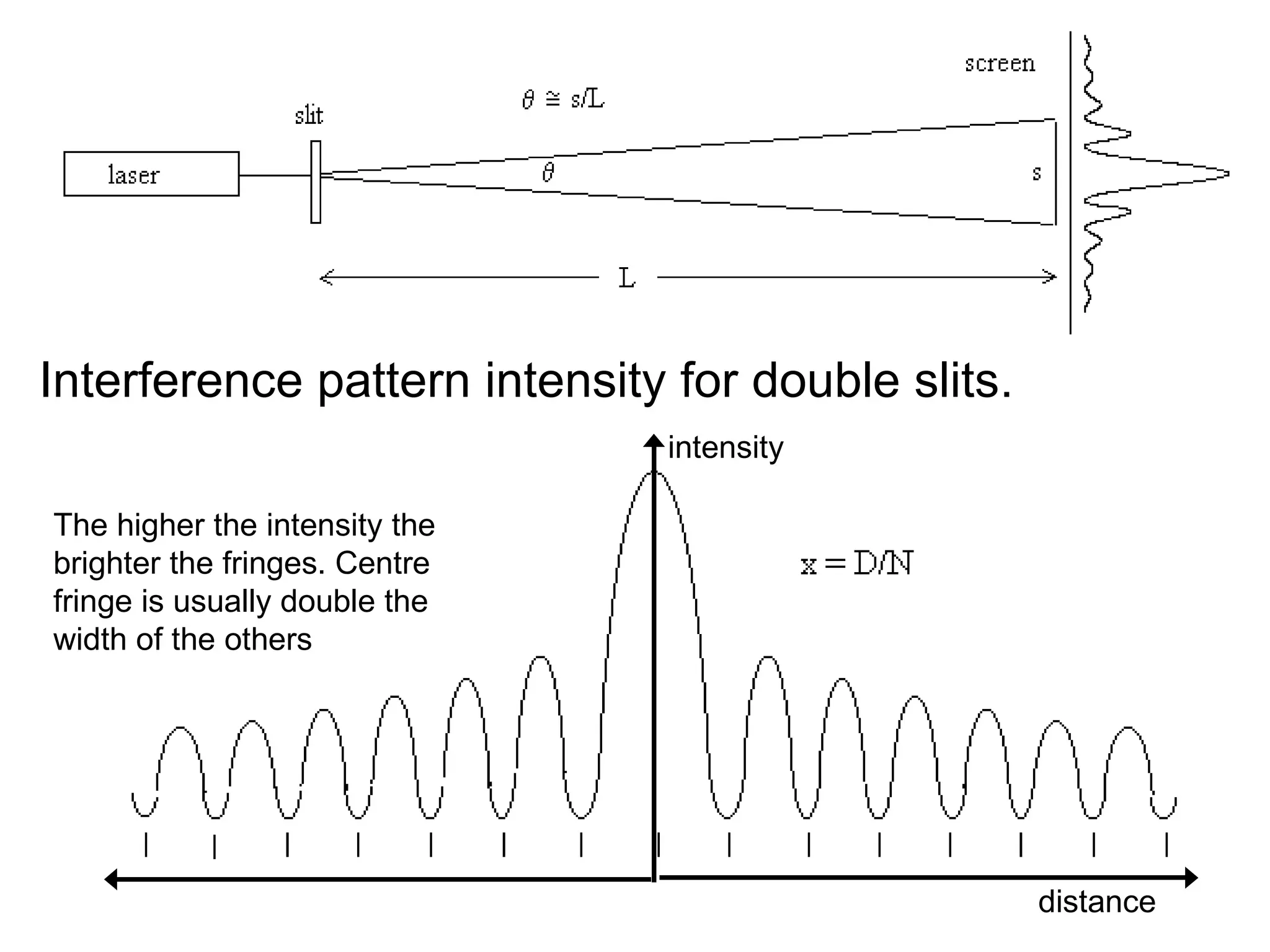
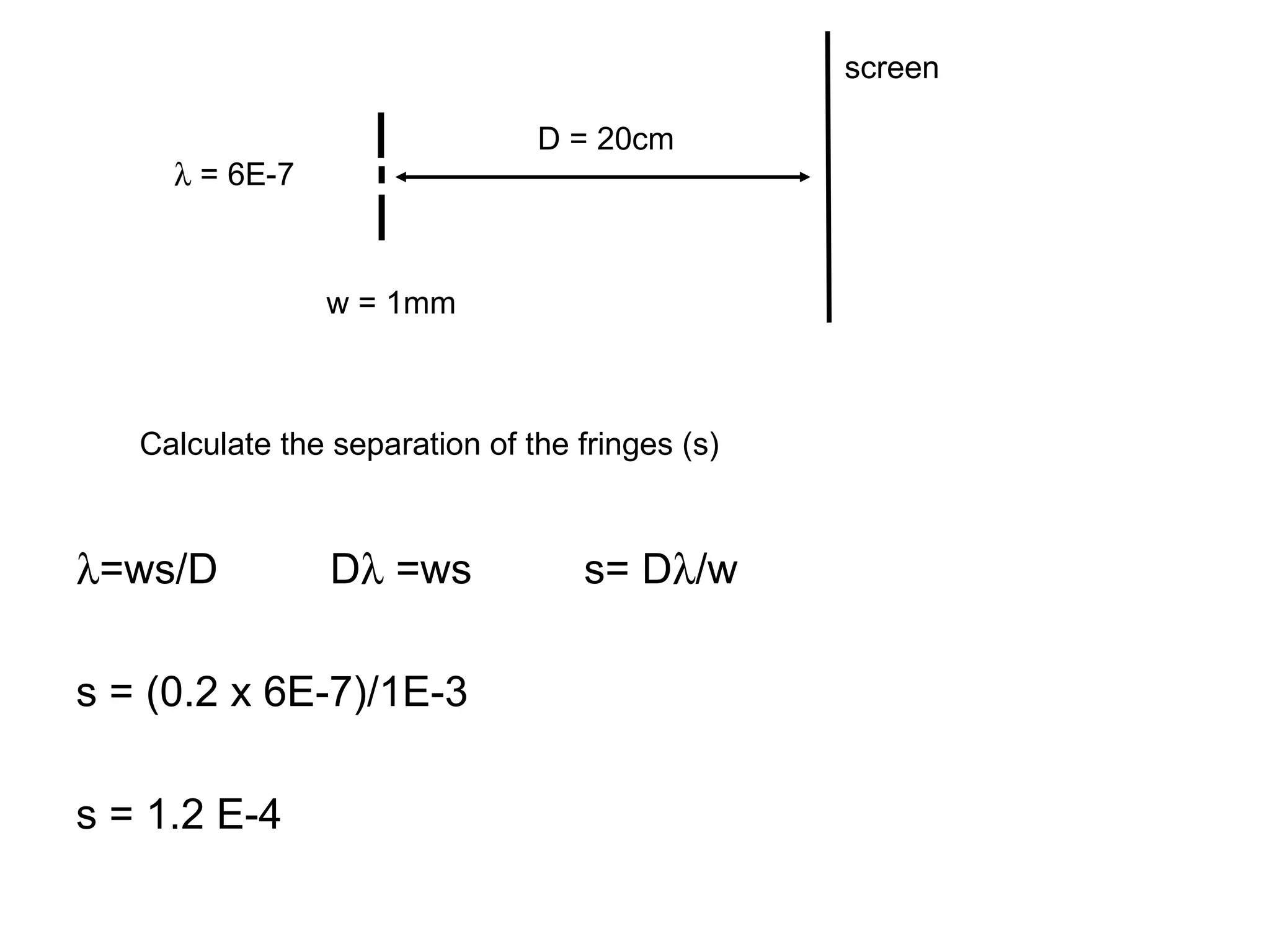
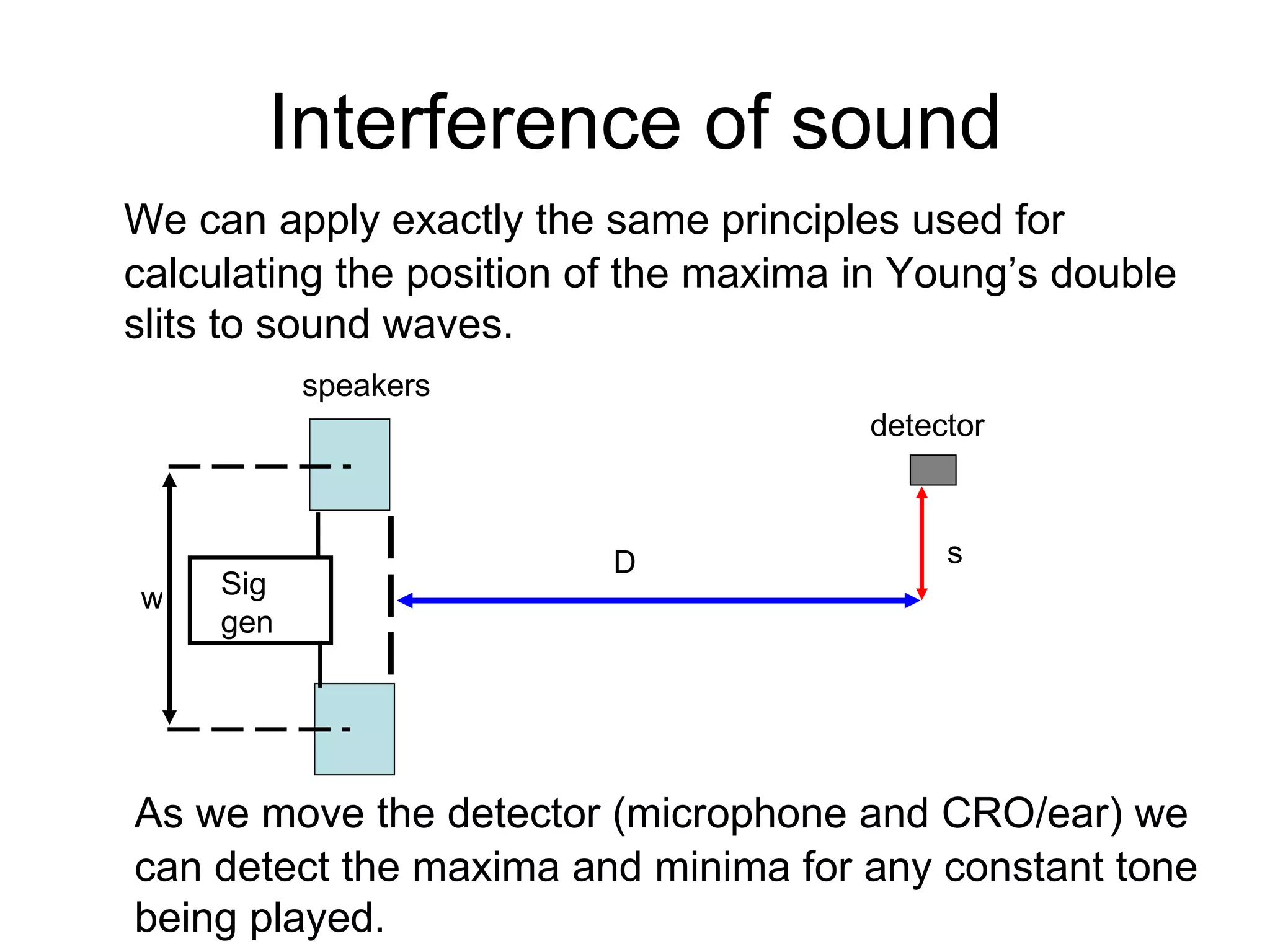
The document discusses interference patterns produced by double slits. When coherent light passes through double slits, it produces a characteristic interference pattern on a screen due to the overlapping waves constructively and destructively interfering. The separation of the bright and dark fringes can be calculated using the formula that relates the wavelength, slit separation, and distance to the screen. Examples are given to demonstrate calculating unknown values when some of the other variables are known. Similar principles of interference patterns apply to sound waves produced by two speakers.

1. Interference in waves Water waves.

3. We can use ripple tanks to explore the ways in which waves interact. The water waves produced behave similarly to all other transverse waves, the behaviour of water waves will have parallels in the behaviour of light for example.

4. Twin sources If we use twin sources, which are in phase and have the same amplitude some very characteristic patterns appear.

5. Draw concentric lines emanating from two point sources. Use alternate solid and dashed lines to represent peaks and troughs

6. Mark points of destructive interference.

7. Connect these marks with straight lines using a ruler

9. If we use double slits this also produces a similar interference pattern as it also gives 2 coherent sets of waves which will affect each other.

11. Young’ double slits. Young’s double slits is a classic experiment examining the interference of light. In this experiment a coherent light source is directed at a pair of slits, the light diffracts as it exits the slits and the overlapping light interferes producing a classic interference pattern. In most explanations and diagrams a single slit is placed between the source and the double slit to produce a coherent light source.

12. We can predict the separation of the maxima produced on the screen using the formula:  = ws D Where: w is the width between the centres of the slits. s is the separation of the fringes. D is the distance between the slits and the screen  is the wavelength of the light source.

13. Interference pattern intensity for double slits. intensity distance The higher the intensity the brighter the fringes. Centre fringe is usually double the width of the others

14.  =ws/D D  =ws s= D  /w s = (0.2 x 6E-7)/1E-3 s = 1.2 E-4  = 6E-7 D = 20cm w = 1mm Calculate the separation of the fringes (s) screen

15. Questions A light source of 420nm is shining through a set of double slits 2mm apart, calculate the distance of the screen if the separation of the bright fringes is 1.6 cm. Calculate the wavelength of the light source if the minima are 1.08mm apart, the slit separation is 3mm and the screen is 4.5m away. If the separation of the maxima is 3mm the screen is at a distance of 6m and the light source has a wavelength of 600nm, calculate the slit separation.

16. Answers A light source of 420nm is shining through a set of double slits 2mm apart, calculate the distance of the screen if the separation of the bright fringes is 1.6 cm.  = ws/D D = ws/  D = (2E-3 x 1.6E-2)/420E-9 D = 76 m Calculate the wavelength of the light source if the minima are 1.08mm apart, the slit separation is 3mm and the screen is 4.5m away.  = ws/D  = (3E-3 x 1.08 E-3)/4.5  = 7.2E-7 (720nm)

17. If the separation of the maxima is 3mm the screen is at a distance of 6m and the light source has a wavelength of 600nm, calculate the slit separation.  = ws/D s =  D/w s = (600E-9 x 6)/3E-3 s = 1.2mm

18. Interference of sound We can apply exactly the same principles used for calculating the position of the maxima in Young’s double slits to sound waves. Sig gen D s w speakers detector As we move the detector (microphone and CRO/ear) we can detect the maxima and minima for any constant tone being played.

19. Questions. A constant tone of 450Hz is being played by speakers 2m apart, what is the separation of the maxima at a distance of 2m? What is the separation at 4m? At 180 KHz what would the separation of the speakers have to be to produce maxima at 2cm intervals at a distance of 4m?

20. Questions. A constant tone of 450Hz is being played by speakers 2m apart, what is the separation of the maxima at a distance of 2m? What is the separation at 4m?  = ws/D s=  D /w (  = c/f = 330/450 = 0.73) s = (0.73 x 2)/2 = 0.73m s= (0.73 x 4)/2 = 1.46m At 180 KHz what would the separation of the speakers have to be to produce maxima at 2cm intervals at a distance of 4m?  = ws/D w=  D /s (  = c/f = 330/180E3 = 1.83E-3) w = (1.83E-3 x 4)/0.02 w = 0.37m