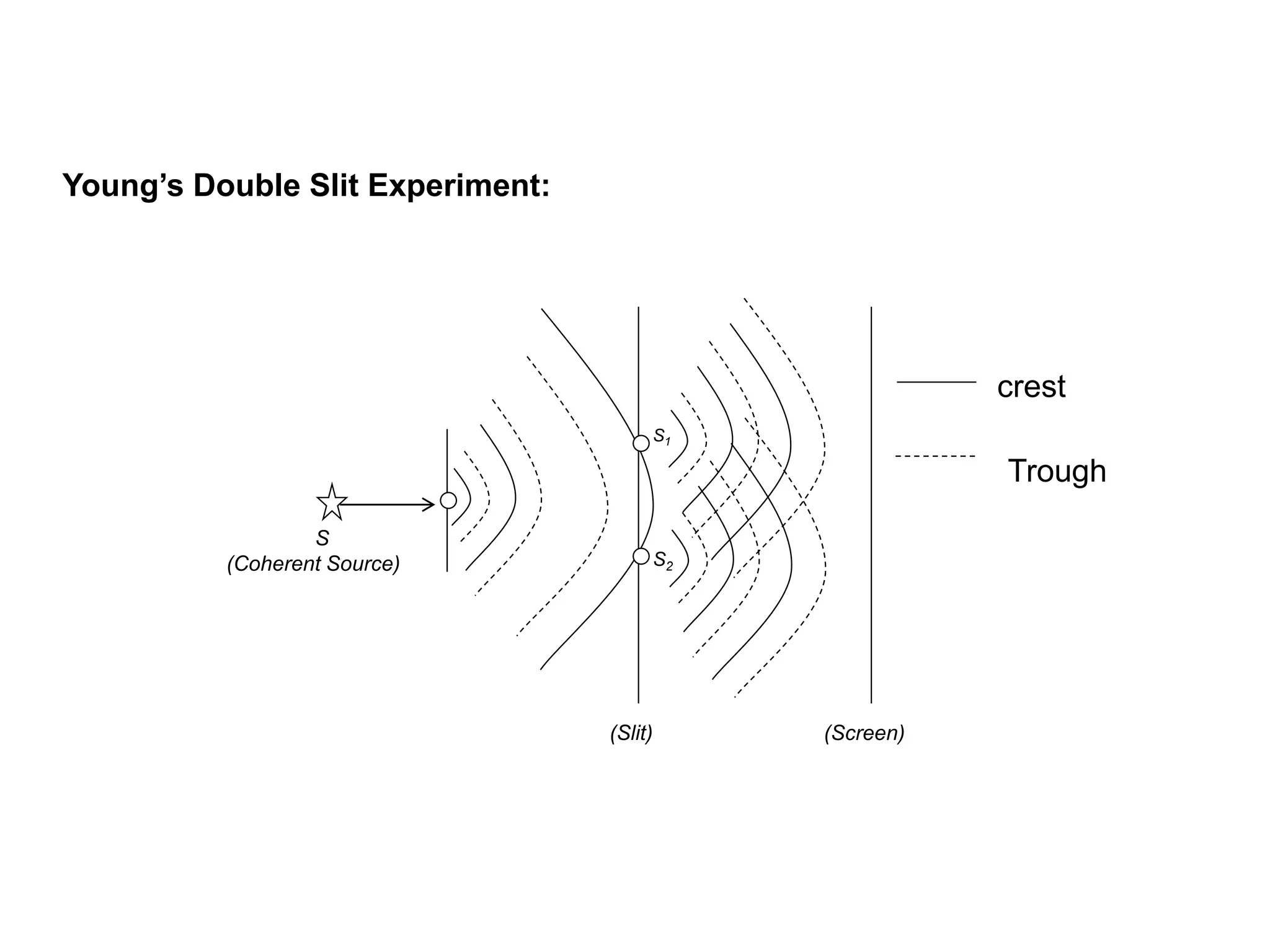
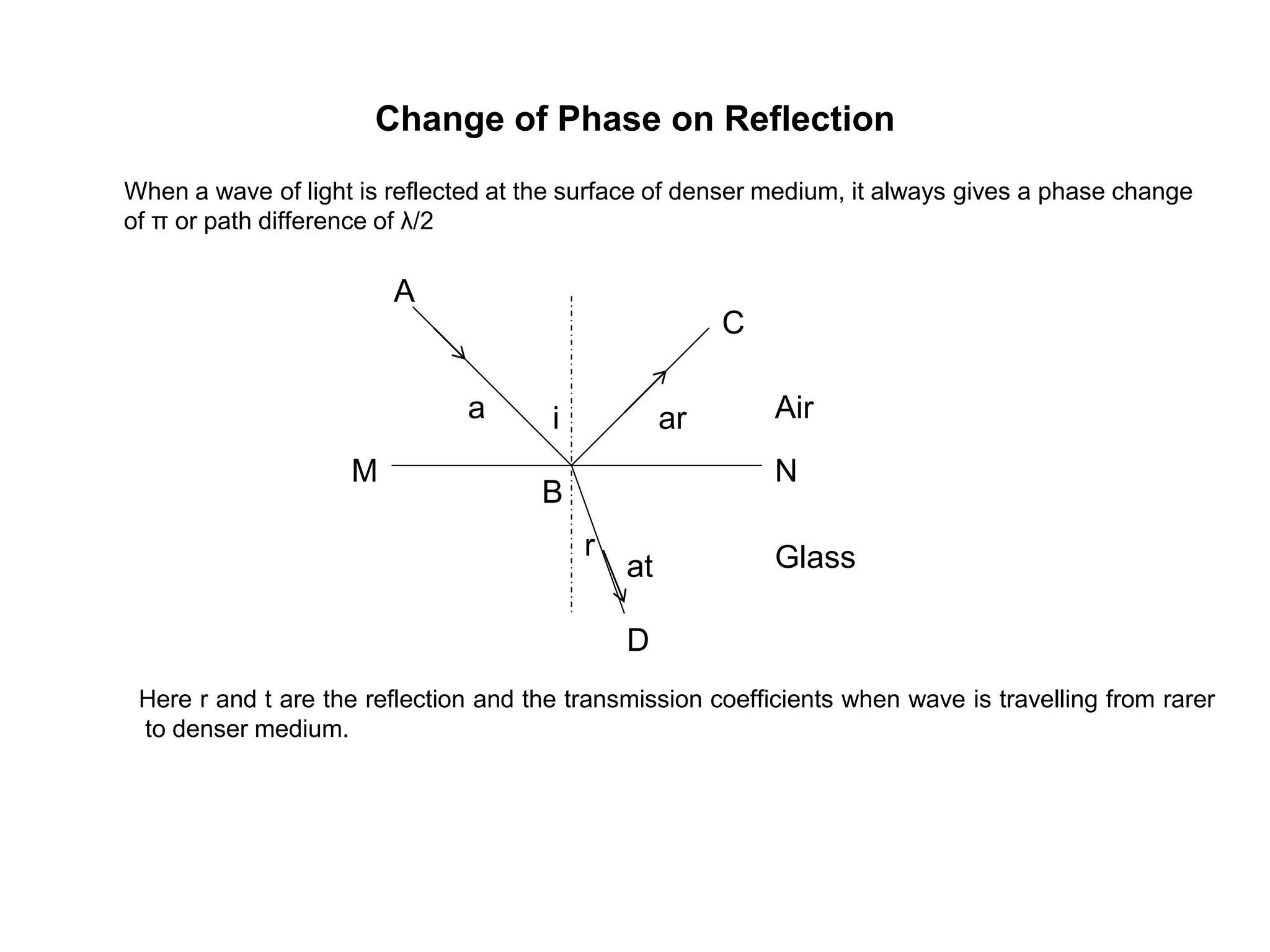
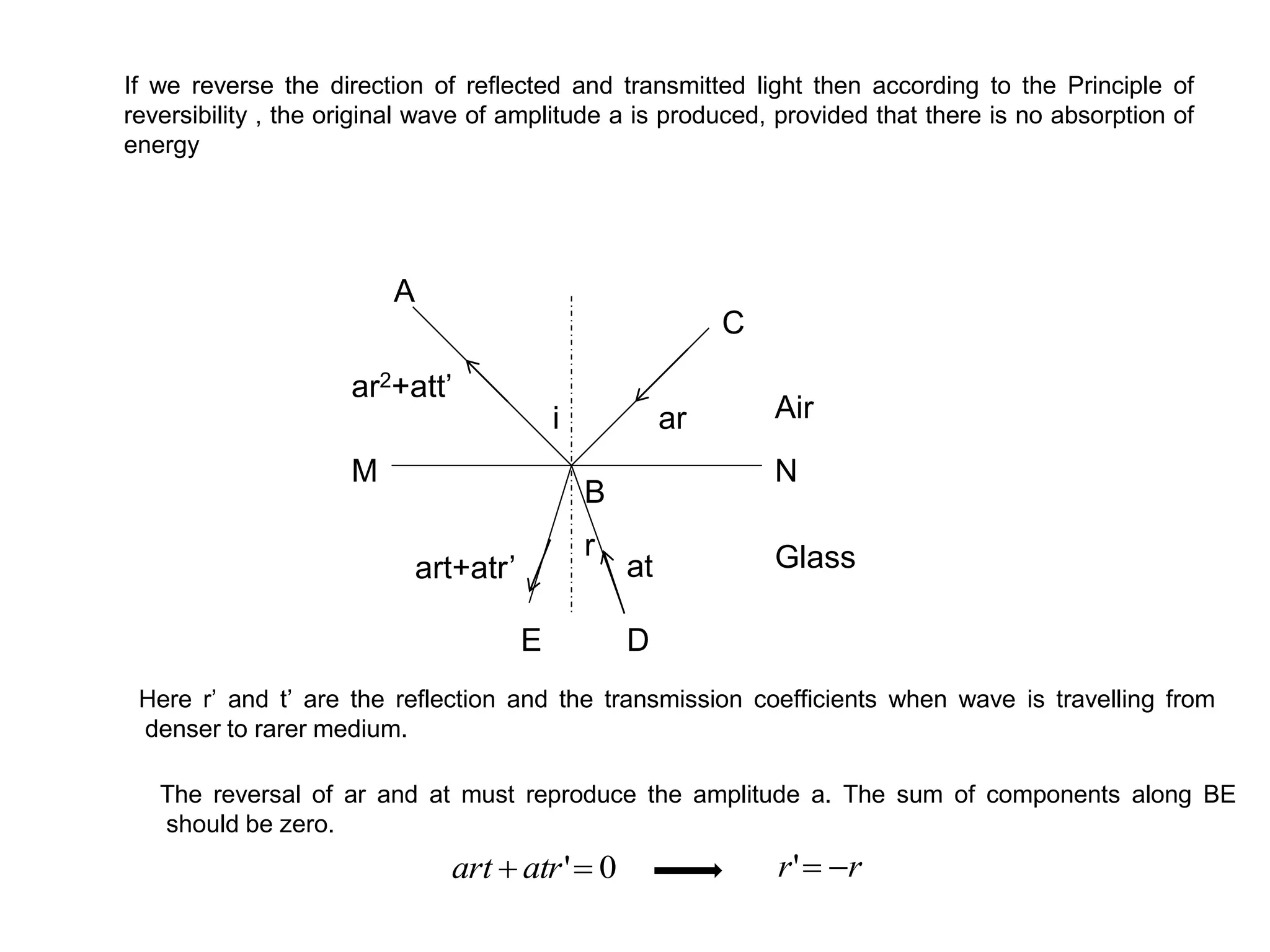
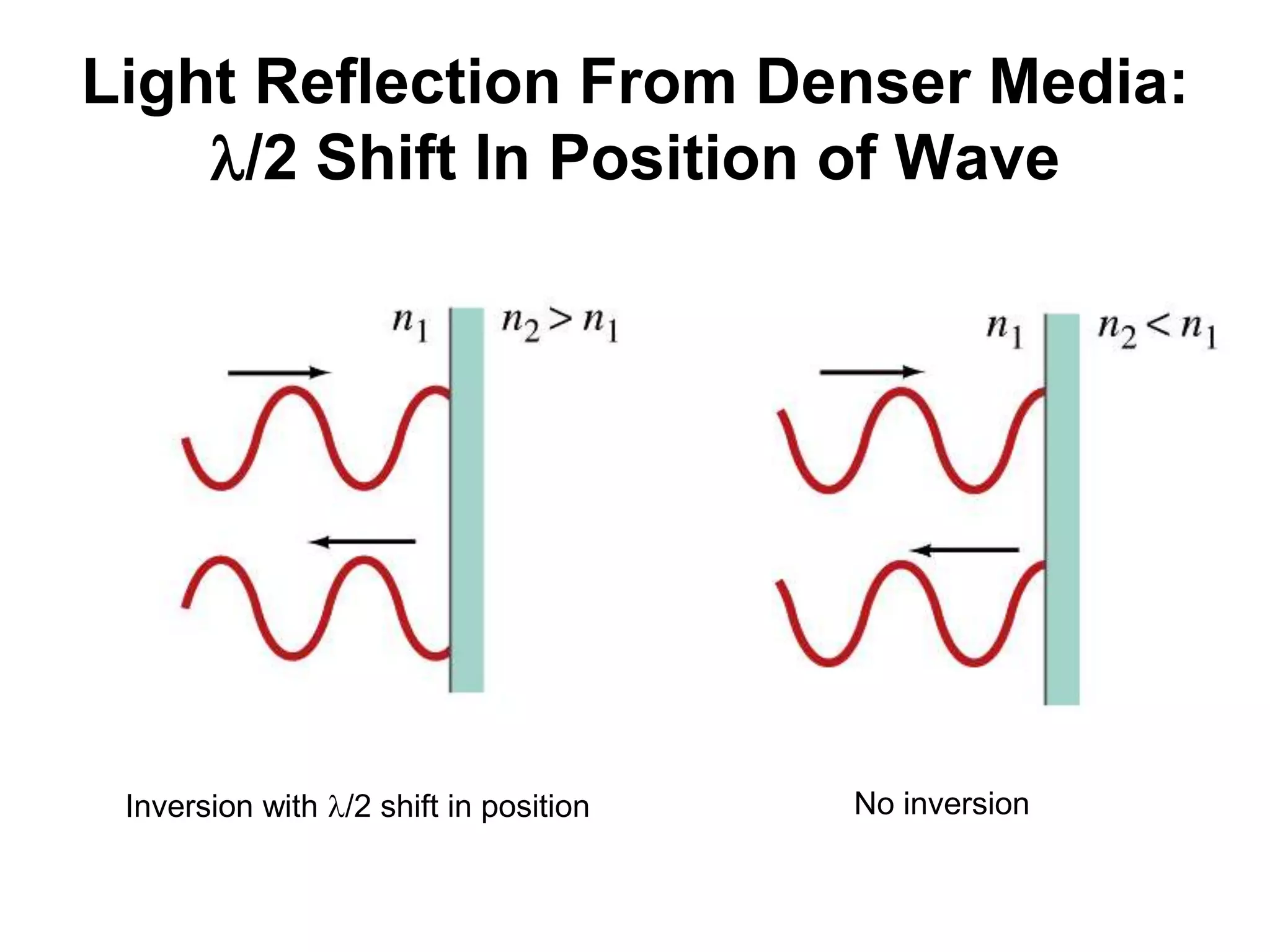
- Interference occurs when two light waves superimpose, resulting in a modification of the intensity of light. This occurs when two coherent sources emit light of the same frequency and constant phase difference. - Constructive interference occurs when the path difference between the waves is equal to an integer multiple of the wavelength, resulting in brighter fringes. Destructive interference occurs when the path difference is an odd integer multiple of half the wavelength, resulting in darker fringes. 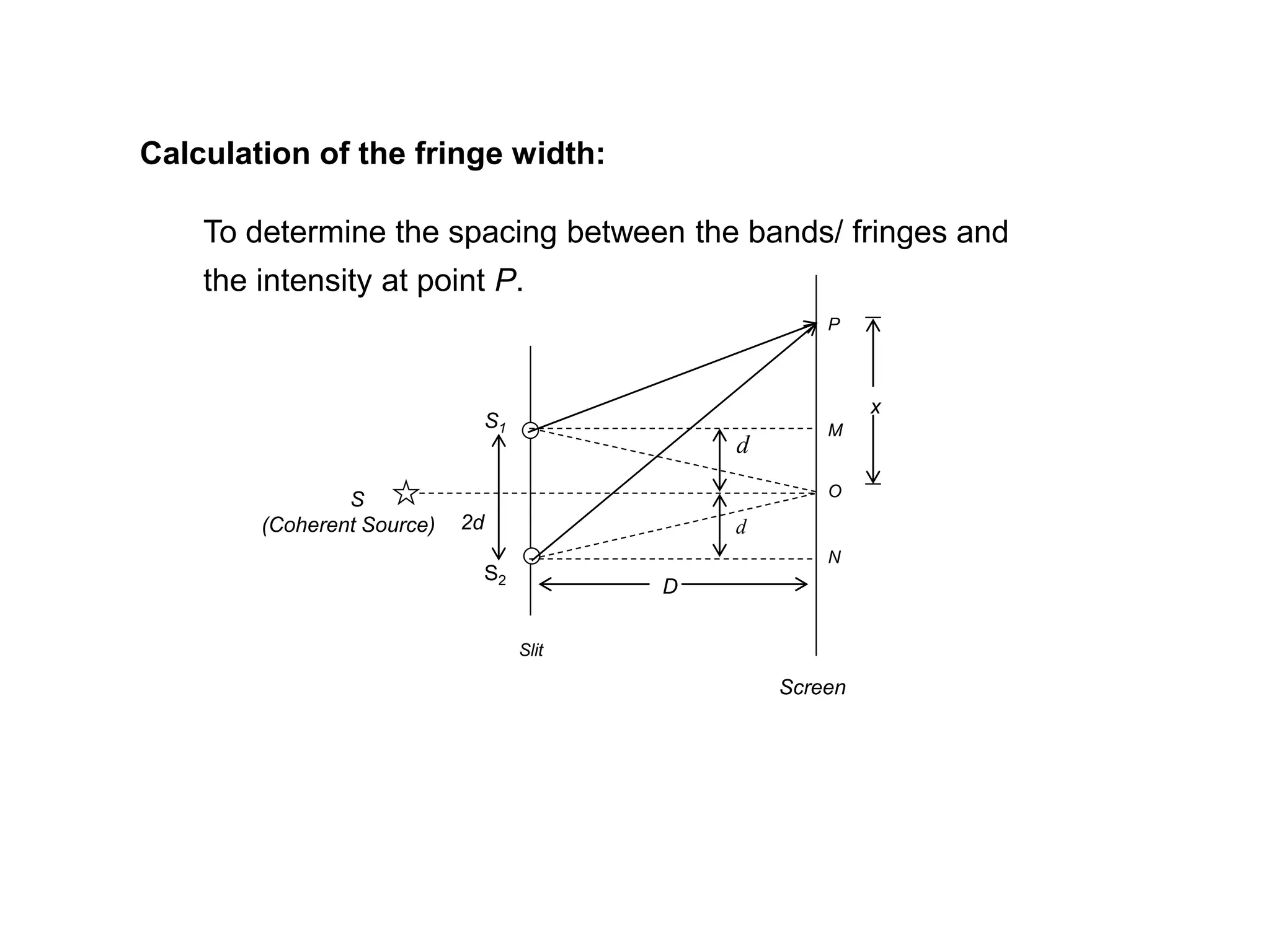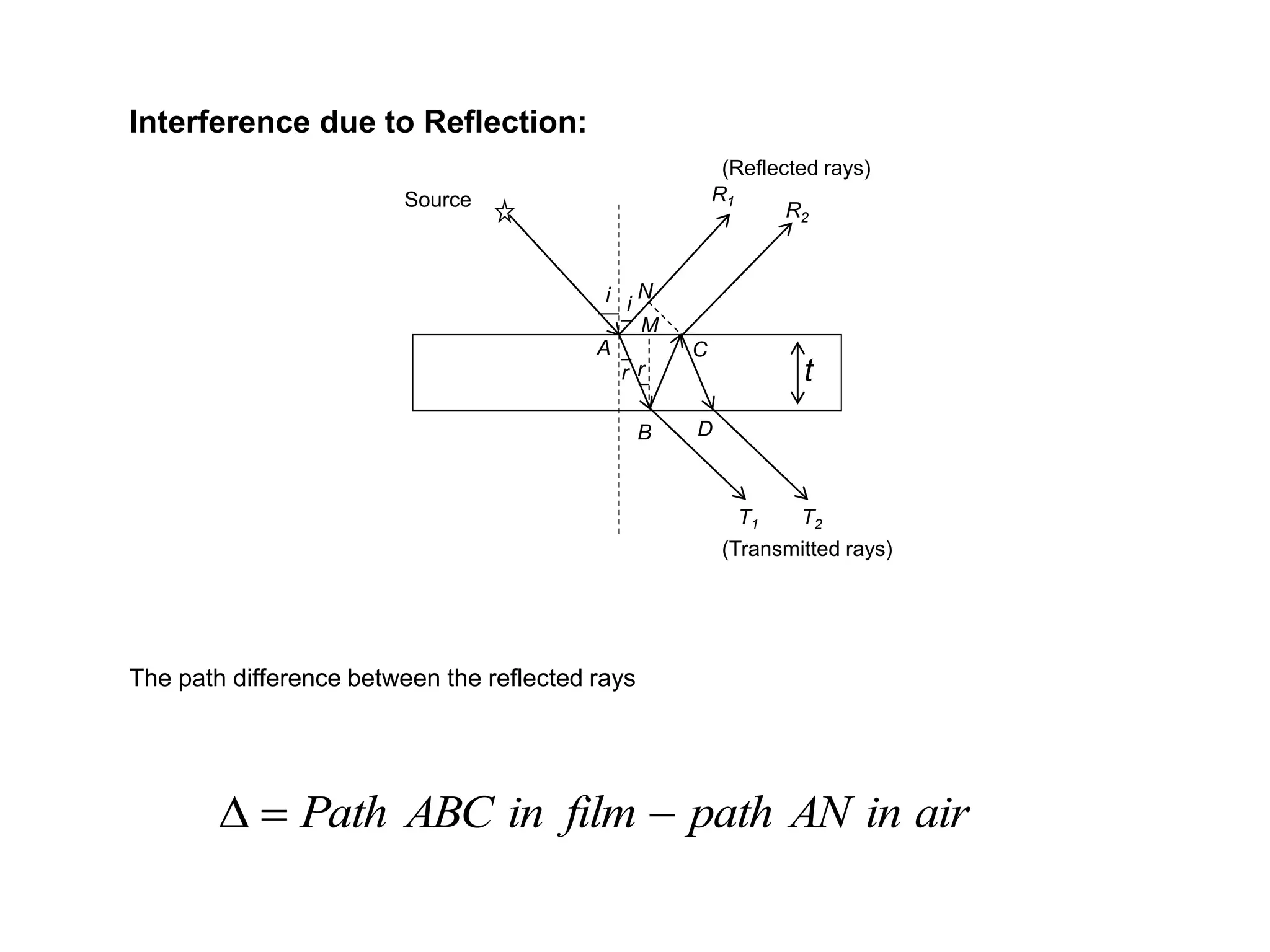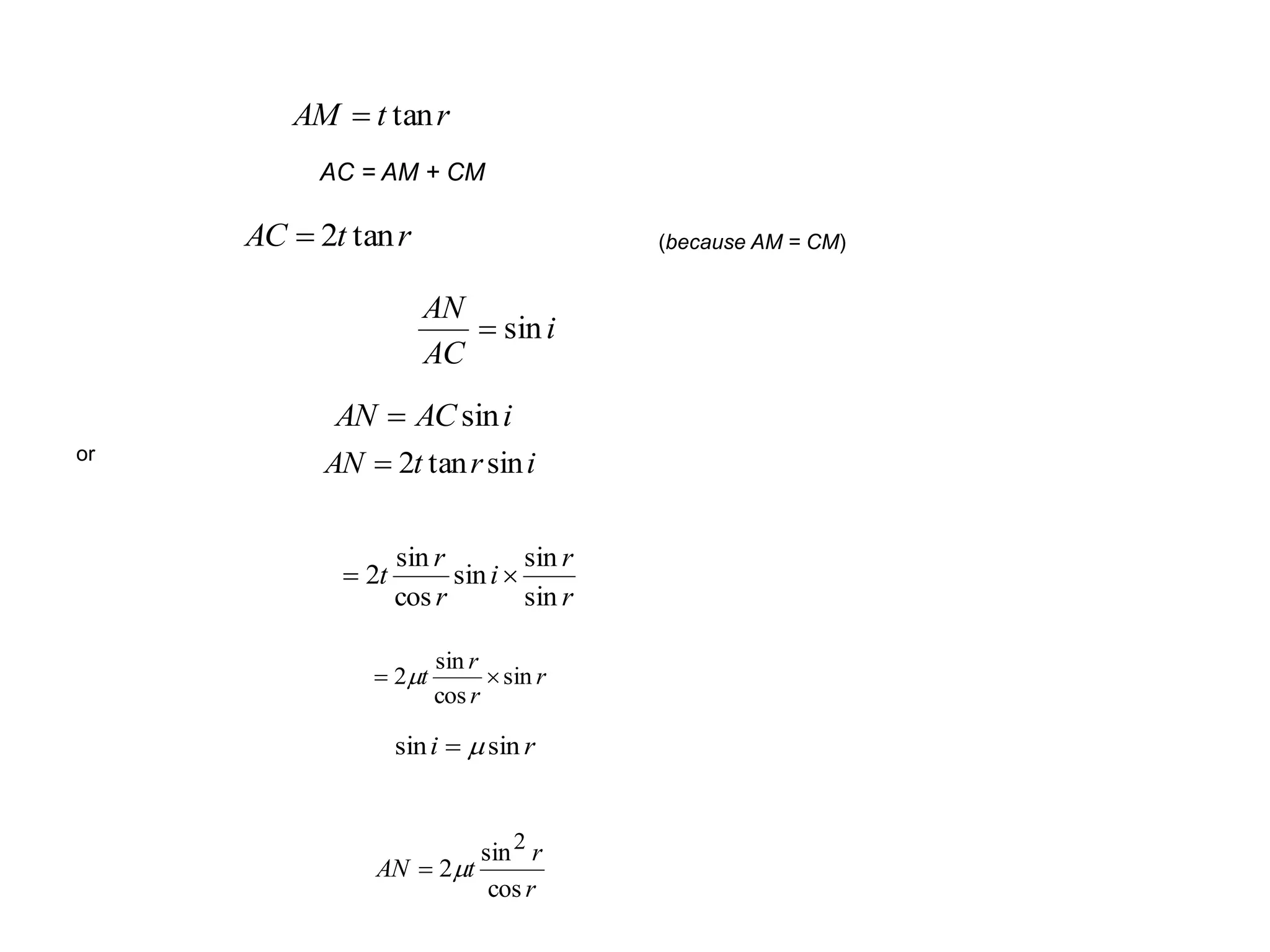- In Young's double slit experiment, the fringe width is directly proportional to the wavelength and distance between the slits and screen, and inversely proportional to the slit separation. The fringe width can be used to determine properties like the thickness of thin sheets.

1. Interference

2. Superposition Principle
For all linear systems, the net response at a given place and time caused by two
or more stimuli is the sum of the responses which would have been caused by
each stimulus individually. So if input A produces response X and input B
produces Y than input (A+B) produces response (X+Y).
Interference
When the light from two different sources with same frequency and having a
constant phase difference move in the same direction, then these light wave trains
superimpose upon each other. This results in the modification of distribution of
intensity of light. This modification of the intensity of light resulting from the
superposition of wave is called interference.
Coherent Sources
Two sources are said to be coherent if they emit light of same frequency and
always having a constant phase difference between them.

3. At some points the resultant intensity is greater than the sum of the intensities of
the waves.
Destructive Interference
Constructive Interference
At some points the resultant intensity is smaller than the sum of the intensities of
the waves.
21 III 
21 III 
This is called Constructive Interference.
This is called Destructive Interference.

4. The wave front originating from a common source is divided into two parts by
using mirrors, prisms or lenses and the two wave fronts thus separated travels and
finally brought together to produce interference.
In this type sources are small like a point source.
Classification of Interference
1. Division of Wave front
2. Division of Amplitude
The amplitude of the incoming beam is divided into two parts either by partial
reflection or refraction. These two parts travel in different paths and finally brought
together to produce interference.
In this type broad sources are required.

5. Young’s Double Slit Experiment:
crest
Trough
S
(Coherent Source)
S1
S2
(Slit) (Screen)

6. Let S be a narrow slit illuminated by a monochromatic light of wavelength λ. S1 and S2
are two narrow slits close to each other and equidistant from S. Suppose is the
frequency of the waves. Let a1 and a2 be the amplitudes of the two wave coming out of
S1 and S2.
Analytical treatment of Interference
tay sin11 

The displacement y1 due to one wave from S1 at any instant t is
The displacement y2 due to other wave from S2 at any instant t is
)sin(22   tay
Where Φ is the constant phase difference between the two waves.
The resultant displacement at P is the algebraic sum of the individual
displacements
21 yyy 

7. )sin(sin 21   tatay
Squaring (i) and (ii) and then adding
 222222
221
22
2
2
1 sincossincos2cos AAaaaaa 
 sincoscossinsin 221 tatatay 
tataay  cossinsin)cos( 221 
 coscos21 Aaa 
 sinsin2 Aa 
tAtAy  cossinsincos 
(i)
(ii)
Let

8. For maximum intensity
1cos 
2
2
2
1max aaI 
or
IAaaaa  2
21
2
2
2
1 cos2 
 n2
2
2121
2
2
2
1max )(2 aaaaaaI 
Phase Difference Path Difference

2
Path Difference = nλ

9. For minimum intensity
1cos 
2
2
2
1min aaI 
or
IAaaaa  2
21
2
2
2
1 cos2 
 )12(  n
2
2121
2
2
2
1min )(2 aaaaaaI 
Phase Difference Path Difference

2
Path Difference
For good contrast
21 aa 
2
max 4aI  0minIand
2
)12(

 n

10. Average intensity


 



2
0
2
0
d
Id
Iav
When a1 = a2

 
 



2
0
2
0
21
2
2
2
1 )cos2(
d
daaaa
 
  



2
0
2
021
2
2
2
1 sin2 aaaa 

2
2
2
1 aaIav 
2
2aIav 

11. Conditions for sustained interference:
Two light sources must be coherent.
Two coherent sources must be narrow, otherwise a single source
will act as a multi sources.
The amplitude of two waves should be equal so that we can get
good contrast between bright and dark fringes.
The distance between two coherent sources must be small.
The distance between two coherent sources and screen should be
reasonable. The large distances of screen reduce to intensity.

12. Calculation of the fringe width:
To determine the spacing between the bands/ fringes and
the intensity at point P.
D
S1
2d
S2
S
(Coherent Source)
Slit
Screen
O
P
d
d
N
M
x

13. Path difference (Δ) = S2P-S1P
To calculate S2P, consider the ∆S2NP
22
2
2
2 NPNSPS 
 222
2 dxDPS 
  2
1
2
2
2 1 




 

D
dx
DPSor
Expending by binomial theorem
 








 2
2
2
2
1
1
D
dx
DPS

14. Therefore, higher power term of D can be neglected. Then we get
 





 
 2
2
2
2
1
D
dx
DPS
 





 

D
dx
DPS
2
2
2or
 dxD Here
Similarly, we can calculate S1P, consider the ∆S1MP
 





 

D
dx
DPS
2
2
1
Then the path difference is (Δ) = S2P - S1P
D
xd2

For the nth fringe the path difference =
D
dxn2

15. (a)Bright Fringes:
The path difference should be equal to n
.
n
D
dxn

2
n
d
D
xn
2
 where n = 0, 1, 2, 3, 4, ----------------
   n
d
D
n
d
D
xx nn
2
1
2
1 
 n
d
D
d
D
n
d
D
222
 
d
D
2


d
D
2

The distance between two consecutive fringes is also known as fringe width.

16.  
2
12

n
 
2
12
2 
 n
D
dxn
 
d
D
nxn
4
12


(b) Dark Fringes:
The path difference should be equal to
Point P to be dark
where n = 0, 1, 2, 3, 4, --------------
d
D
d
D
xx nn
24
2
1



d
D
2

Fringe width

17.  D
  







d
1

From the above equations, it is clear that fringe width β depends on
1. It is directly proportional to the distance between two coherent sources
and screen
2. It is directly proportional to the wavelength of light
3. It is inversely proportional to the spacing between two coherent sources
.

18. Fresnel’s Biprism:
Fresnel’s biprism is a device to produce two coherent
sources by division of wave front.
D
ba
Overlap
regionS
S2
S1
O
H
P
G
Q

19. Construction:
A biprism consists of a combination of two acute angled prisms placed
base to base.
The obtuse angle of the biprism is 179º and other two acute angles are 30’.
03 
03 
179°

20. (b) Determination of the distance between two virtual sources:
Displacement method is one of the methods to calculate the distance
between two virtual coherent sources:
U’
vu
v’
 
  lensandobjectbetweencedis
lensandimagebetweencedis
Oobjecttheofsize
Iimagetheofsize
tan
tan

According to the linear magnification produced by the lens:
Further the lens moves towards the eyepiece and a focused image of virtual
sources S1 and S2 is visible in eyepiece again. This time the image separation of S1 and
S2 should be appear different (d2) so that:
u
v
d
d
1
'
'2
u
v
d
d

(1)
(2)
d1d2
L2L1
S1
S2
d

21. 1
2
d
d
d
d

21
2 ddd 
21ddd 
From equation (1) and (3), we get
or
But 'vu  and 'uv 
Thus equation (2) becomes
v
u
d
d
2
(3)

22. Applications of Fresnel’s Biprism:
Determination of thickness of thin sheet of transparent
material like glass or mica.
or
How to calculate the displacement of fringes when a mica
sheet is introduced in the path of interfering rays?
S1
2d
S2
t
x
D
Pm
O

23. v
t
c
tPS
T 

 1
c
t
c
tPS
T
m


 1
The time taken by light to reach P from S1 is
v
c
mBut
ttPScT m 1
  ttPSPS m 12
The path difference S2P and S1P will then be given by

24. The path difference between S2P and S1P is
   m nttPSPS  12
  m ntPSPS  112or
We have already calculated that  PSPS 12 
D
dxn2

  m nt
D
dxn
 1
2
  m nt
d
D
xn  1
2
or
Let the point P is the center of the nth bright fringe if the path difference is equal to nλ
Where xnis the distance of the nth bright fringe from the central fringe in the absence of mica.
The position of the central bright fringe when the mica sheet is placed in
the path S1P is obtained by putting n=0 in equation (1) we get
(1)

25.   t
d
D
x 1
2
0  m
m 0xSince >1 so that is positive.
(2)
The fringe width is
 
d
D
xx nn
2
1

   Using equation (1)
It means the fringe width is not affected by introduce of mica sheet.



d
D
2
Put these values in equation (2) we get,
 1
2 0


mD
dx
t
 1
0


m
x
tor
Thus we can calculate the thickness of mica sheet.

26. Light Reflection From Denser Media:
/2 Shift In Position of Wave
Inversion with /2 shift in position No inversion

27. Change of Phase on Reflection
When a wave of light is reflected at the surface of denser medium, it always gives a phase change
of π or path difference of λ/2
i Air
Glass
ar
at
r
NM
D
C
B
A
a
Here r and t are the reflection and the transmission coefficients when wave is travelling from rarer
to denser medium.

28. If we reverse the direction of reflected and transmitted light then according to the Principle of
reversibility , the original wave of amplitude a is produced, provided that there is no absorption of
energy
i Air
Glass
ar
at
r
NM
D
C
B
A
ar2+att’
art+atr’
Here r’ and t’ are the reflection and the transmission coefficients when wave is travelling from
denser to rarer medium.
The reversal of ar and at must reproduce the amplitude a. The sum of components along BE
should be zero.
0' atrart rr '
E

29. Interference due to Reflection:
Source
t
airinANpathfilminABCPath 
ii
rr
R1
R2
T1 T2
A
B
C
D
M
N
(Reflected rays)
(Transmitted rays)
The path difference between the reflected rays

30.   ANBCAB  m
r
AB
BM
cos

r
t
AB
cos

r
t
BC
cos
  BCAB 
r
BM
AM
tan
rBMAM tan
(1)
BM = t
and also
Now, for AN

31. rtAM tan
rtAC tan2
i
AC
AN
sin
iACAN sin
irtAN sintan2
r
r
i
r
r
t
sin
sin
sin
cos
sin
2 
r
r
r
t sin
cos
sin
2  m
ri sinsin m
r
r
tAN
cos
sin
2
2
m
AC = AM + CM
(because AM = CM)
or

32. r
r
t
r
t
r
t
cos
sin
2
coscos
2
mm 






r
r
t
r
t
cos
sin
2
cos
2 2
m
m

 r
r
t 2sin1
cos
2

m
r
r
t 2cos
cos
2m

rt cos2m
So that,
So that the actual path difference:
2
cos2

m  rt
As the ray is reflected from a denser medium, so an addition of
path difference of λ/2 will be there.

33. So for Maximum Intensity, path difference should be equal to
m nrt cos2


m nrt 
2
cos2
n
2
)12(cos2

m  nrt
Where n = 0,1,2,3,4,5…………………..
So for Minimum Intensity, path difference should be equal to
2
)12(

n
2
)12(
2
cos2

m  nrt
Where n = 0,1,2,3,4,5…………………..
Interference will not be perfect as there is difference in the amplitude of the reflected rays.

34. Production of colors in thin films:
When a thin film of oil on water, or a soap bubble, exposed to white light (such as
sunlight) is observed under the reflected light. The brilliant colors are seen due to
the following reasons
The path difference depend on the wavelength. It means the path
difference will be different for different colors, so that with the white light
the film shows various colors from violet to red.
The path difference also varies with the thickness of film so that various
colors appear for the same angle of incidence when seen in white light.
The path difference changes with the angle r and angle r changes with
angle i. So that the films assumes various colors when viewed from
different directions with white light.

35. Newton’s Rings:
Source
   
2
cos2

m  rt
 
2
cos2

m  rt
Actually the path difference between the interfering rays is
The effective path difference for large radius of curvature or for small angle θ

36. 

m nt 
2
2
 
2
122

m  nt
 
2
12
2
2

m  nt
  

m nnt 
22
122
m nt 2
For normal incidence cosr =1, then the path difference  
2
2

m  t
For maxima
For minima

37. Why Central Ring is dark in Newton’s rings experiment
 
2
2

m  t
At point of contact t = 0
 
2


Path difference for dark ring  
2
12

n
For n = 0, Path difference
2


That’s why Central Ring is dark

38. How to calculate the radius or diameter of the nth fringe:
n
22 2 tRtn 
Rt 2
Rtn 22 
R
t n
2
2

Let be the radius of bright ring at point C and t is the thickness of air film at that point.
Let R be the radius of plano-convex lens. In triangle OAC
so that the higher power terms are neglected.
Therefore, we have
ρn
R
R
R-t
O
A
B
C
D
RttRR n 22222
 
 222
tRR n  
or
But t

39.  
2
122

m  nt
 
2
12
2
2
2

m  n
R
n
 
m


2
122 R
nn 
For constructive interference: We have,
 





 

m


2
12nR
n
 





 

m


2
12
22
nR
D nnDiameter
   
m

m
 122
2
1242 



nRnR
Dn

40. 1mNow, for the air film the refractive index
Therefore,
Therefore,
 1222
 nRDn
12 nDn
Diameter of the nth bright ring is proportional to the square root of the odd natural numbers
For Dark rings
m nt 2
m n
R
pn

2
2
2
1mBut for air film
So,
Rnpn 2

41. Therefore,
RnDn 42

nDn
Diameter of the nth dark ring is proportional to the square root of the natural numbers
Rnpn 

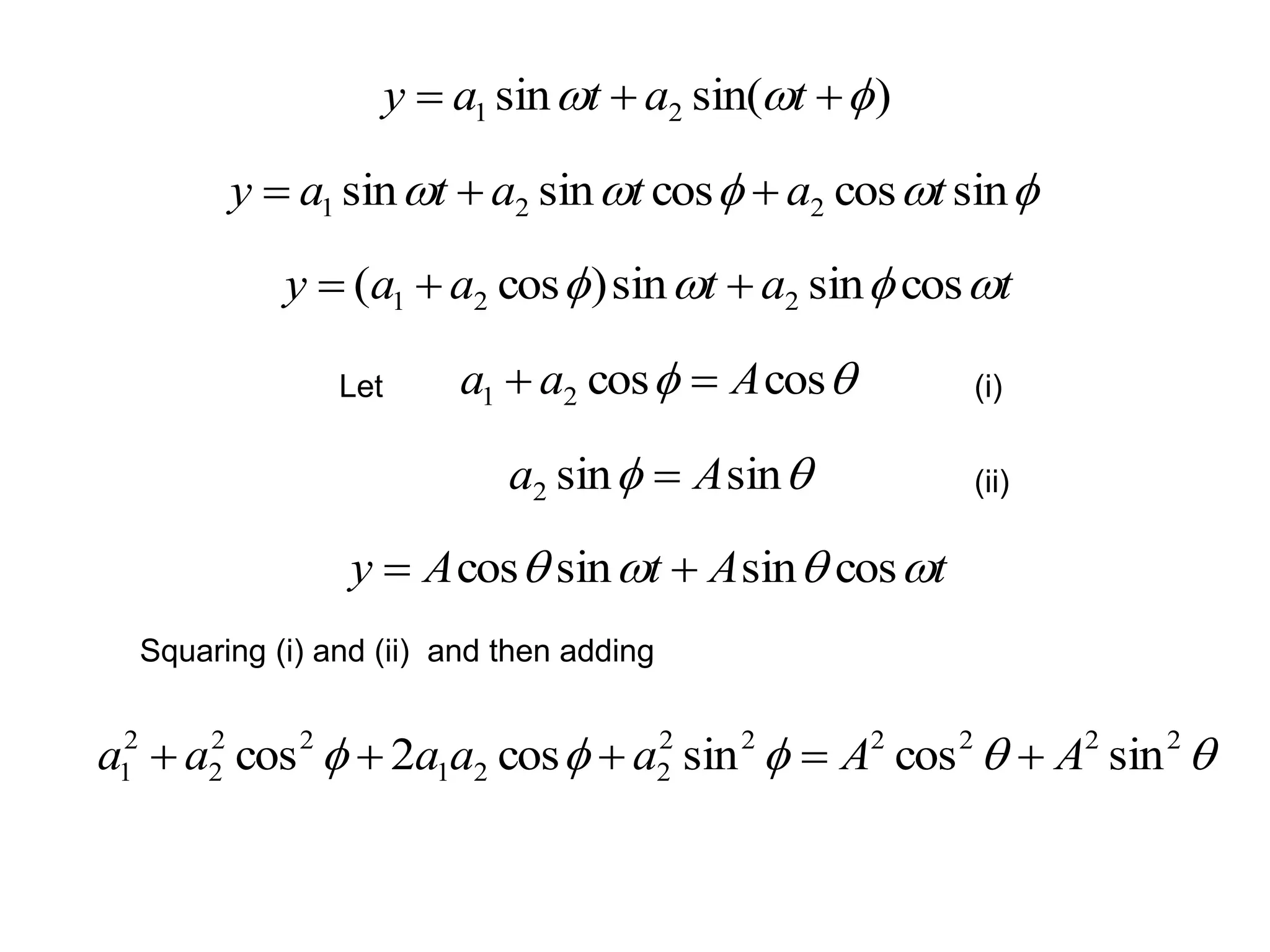
42. Spacing between successive rings
This shows that the spacing decreases with increase in the order of the rings.
]1[1 nnkDD nn 
]12[12  kDD
]23[23  kDD
]34[34  kDD

43.     1222
 pnRD pn
       12212222
 nRpnRDD npn
 RnRRpRnR 24244 
  pRDD npn
422 

 
pR
DD npn
4
22 



Determination of wavelength of light by Newton’s Rings method
 thpn Now the diameter of bright ring,
Therefore,
 1222
 nRDn

44. For Air film,
RnD airn 4][ 2

Determination of refractive index of unknown liquid by Newton’s Rings method
For unknown liquid with refractive index m
m
Rn
D liquidn
4
][ 2

liquidn
airn
D
D
][
][
2
2
m