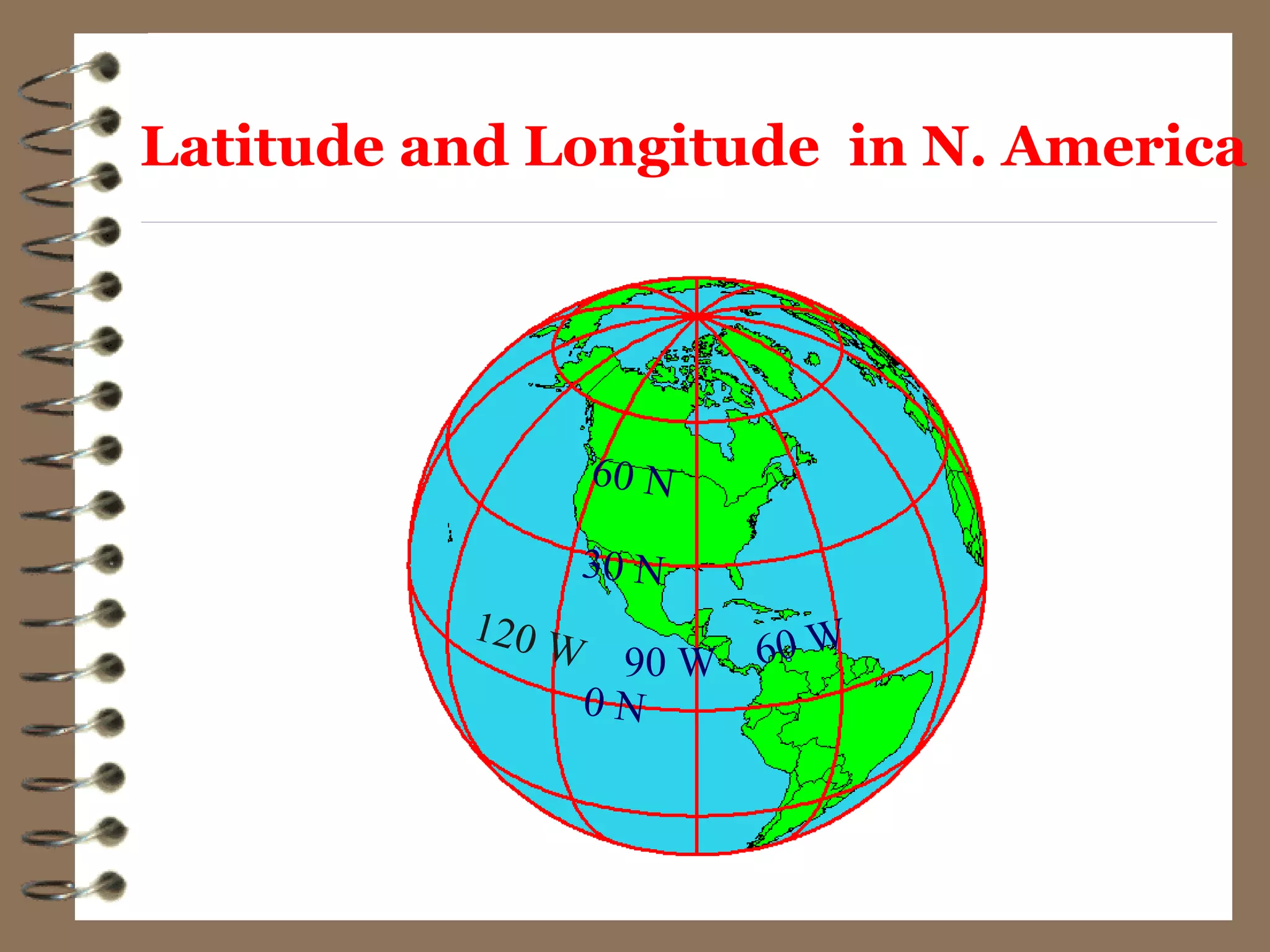
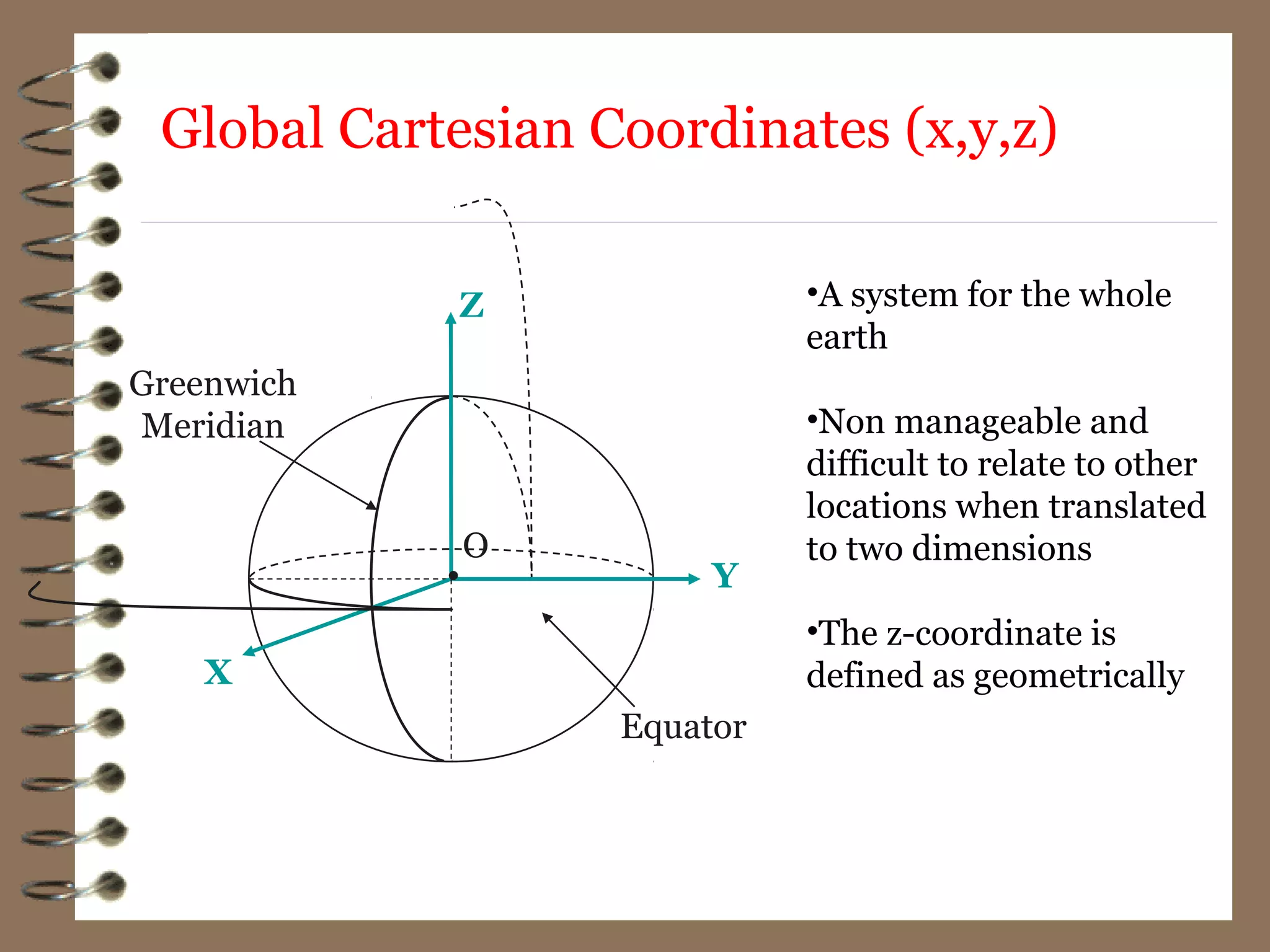
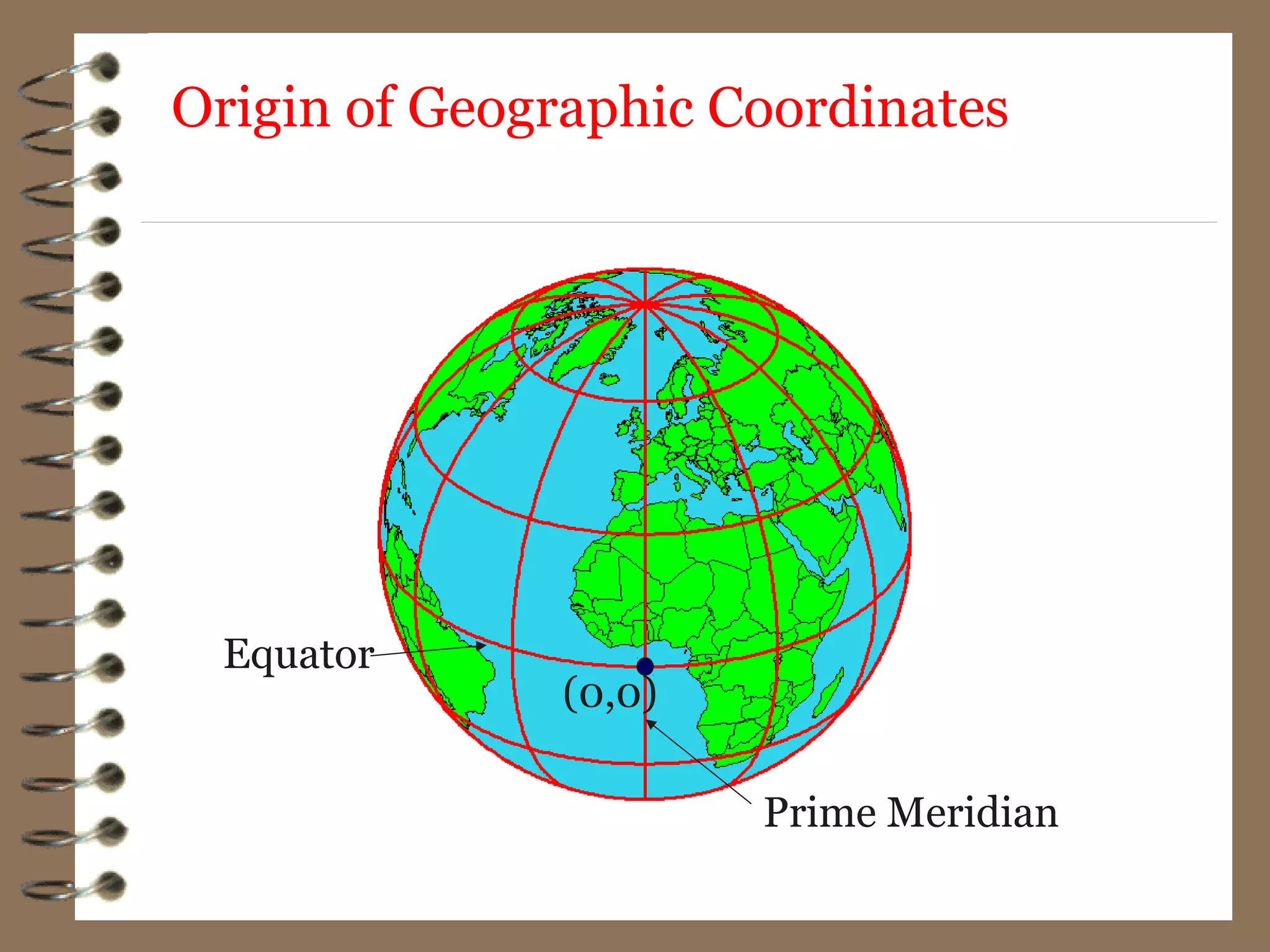
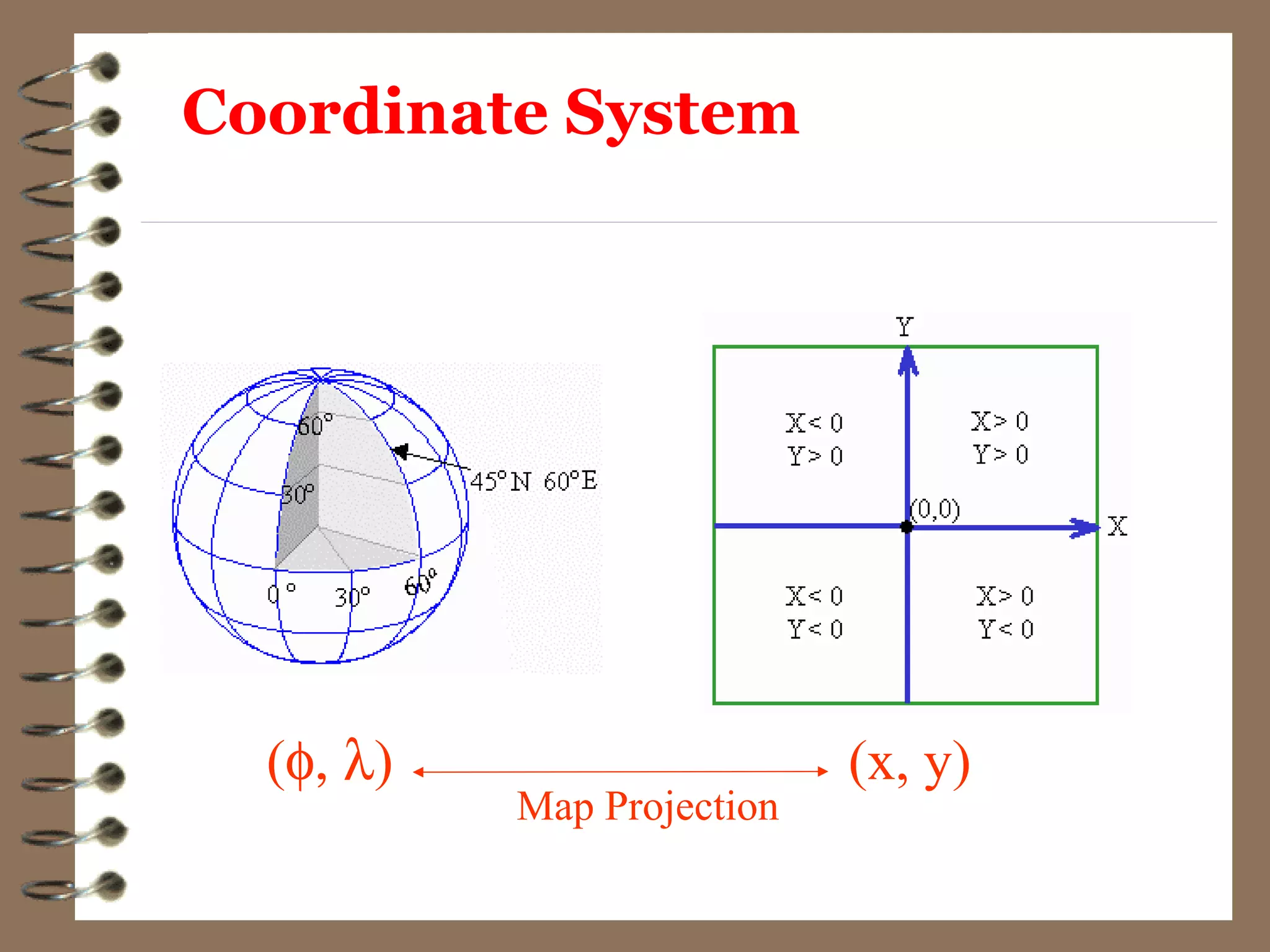
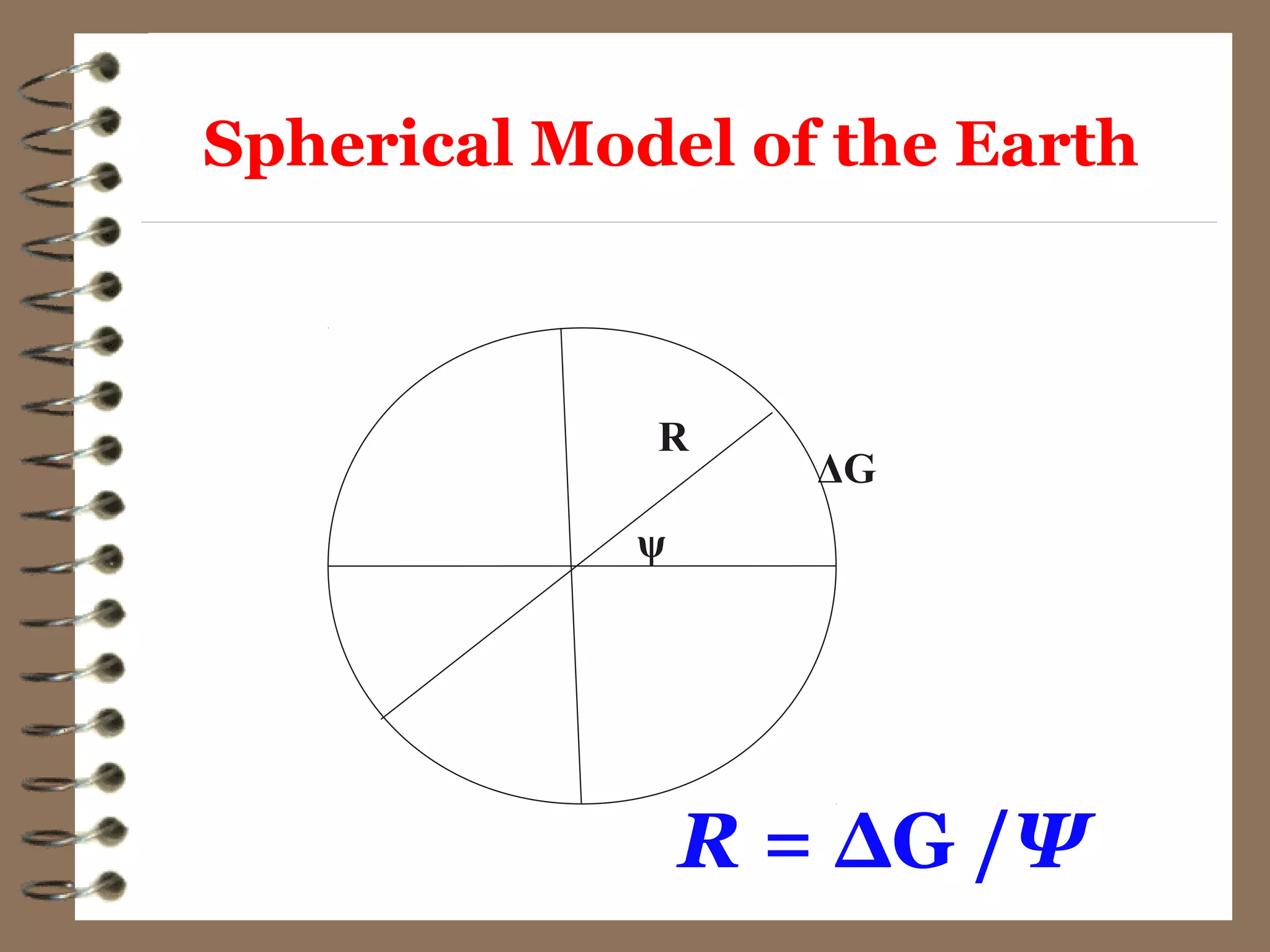
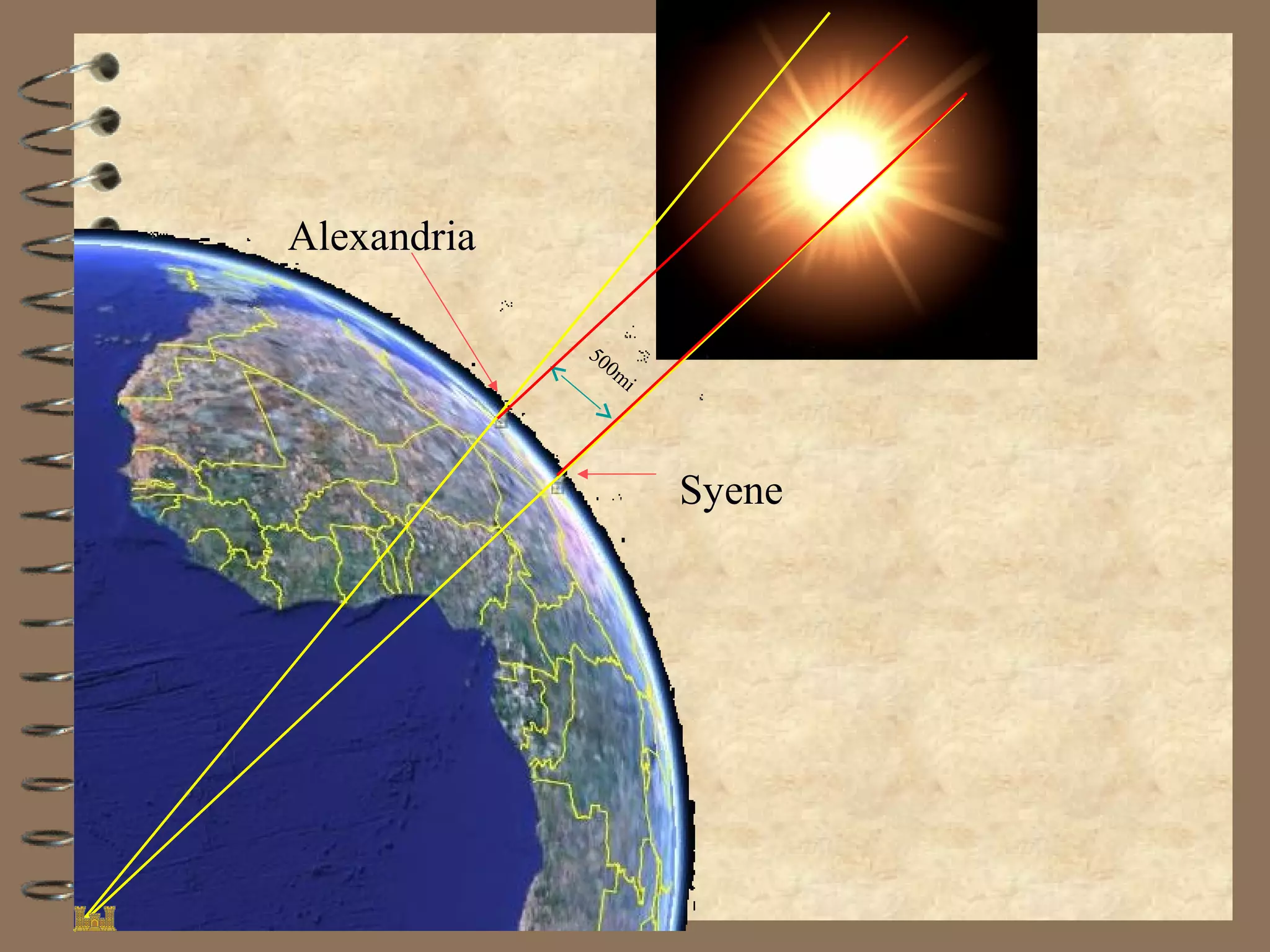
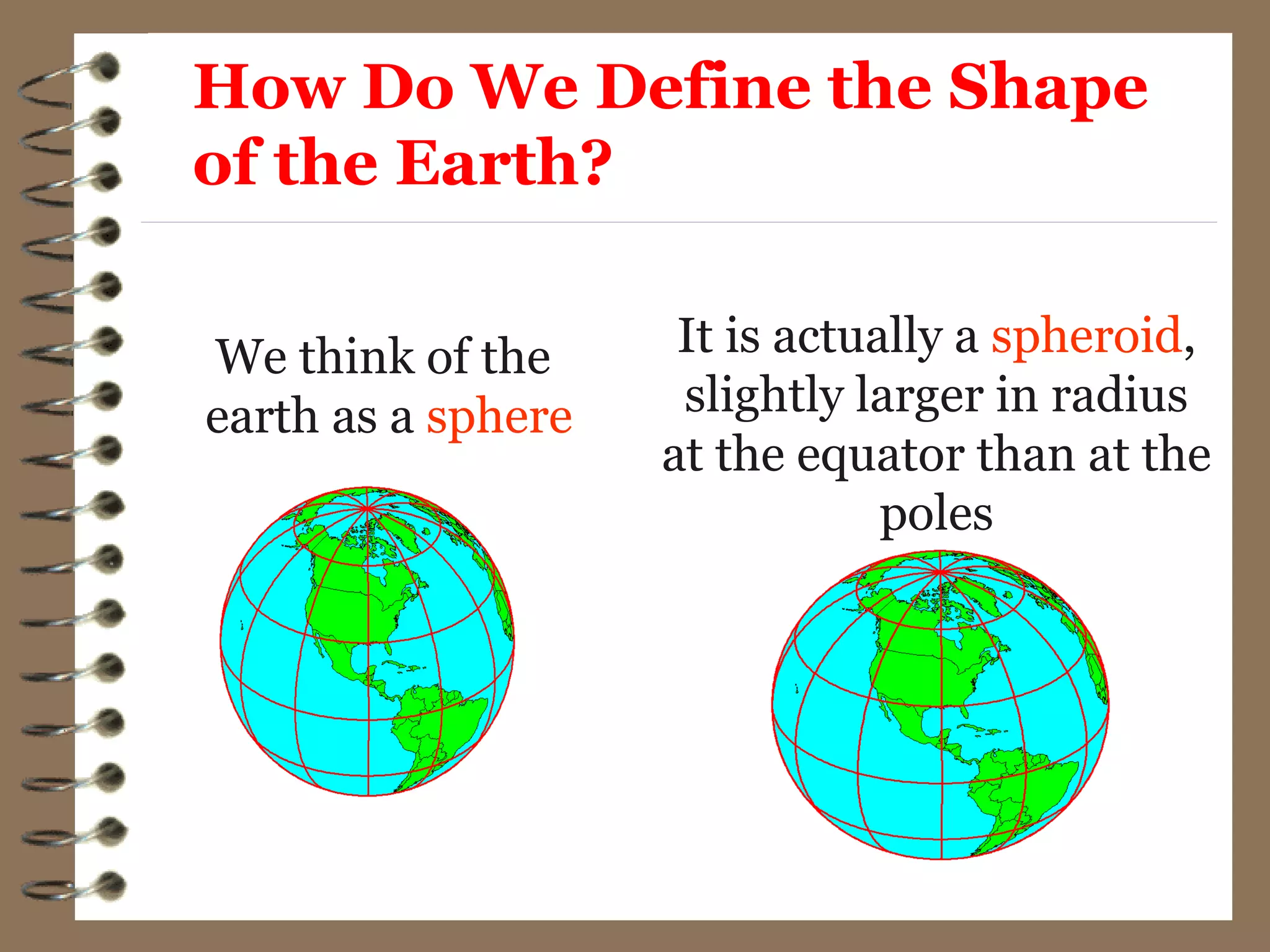
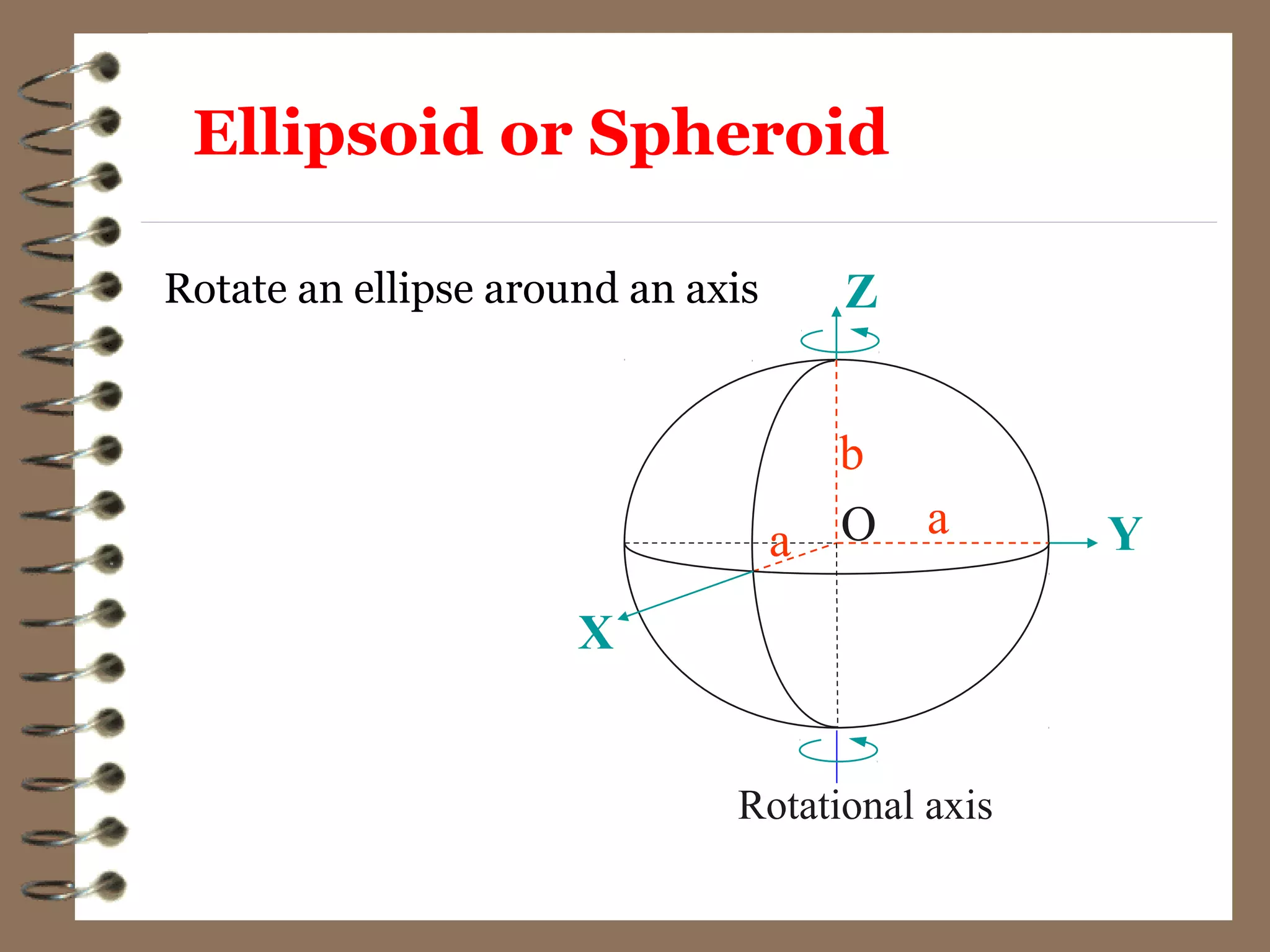
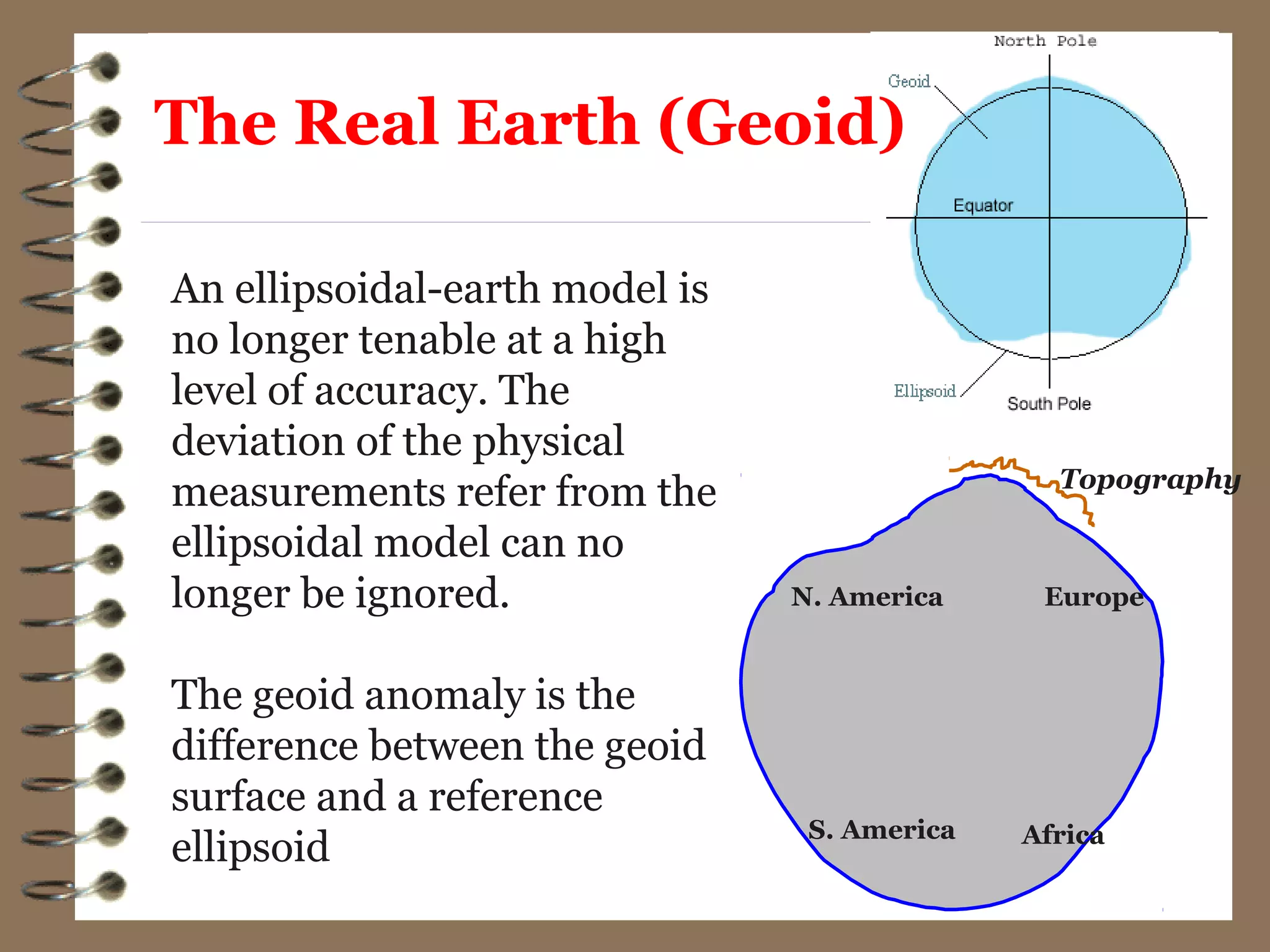
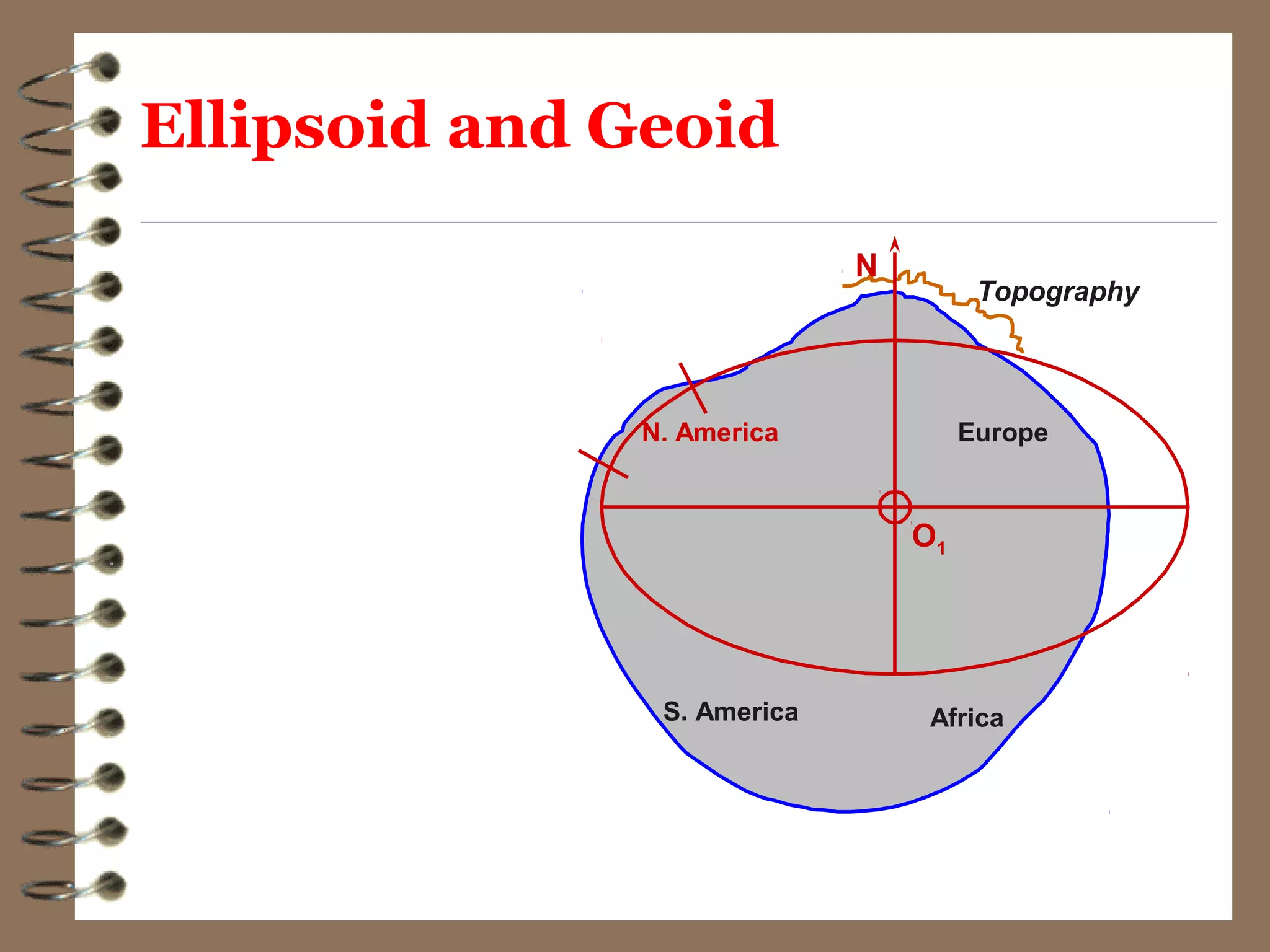
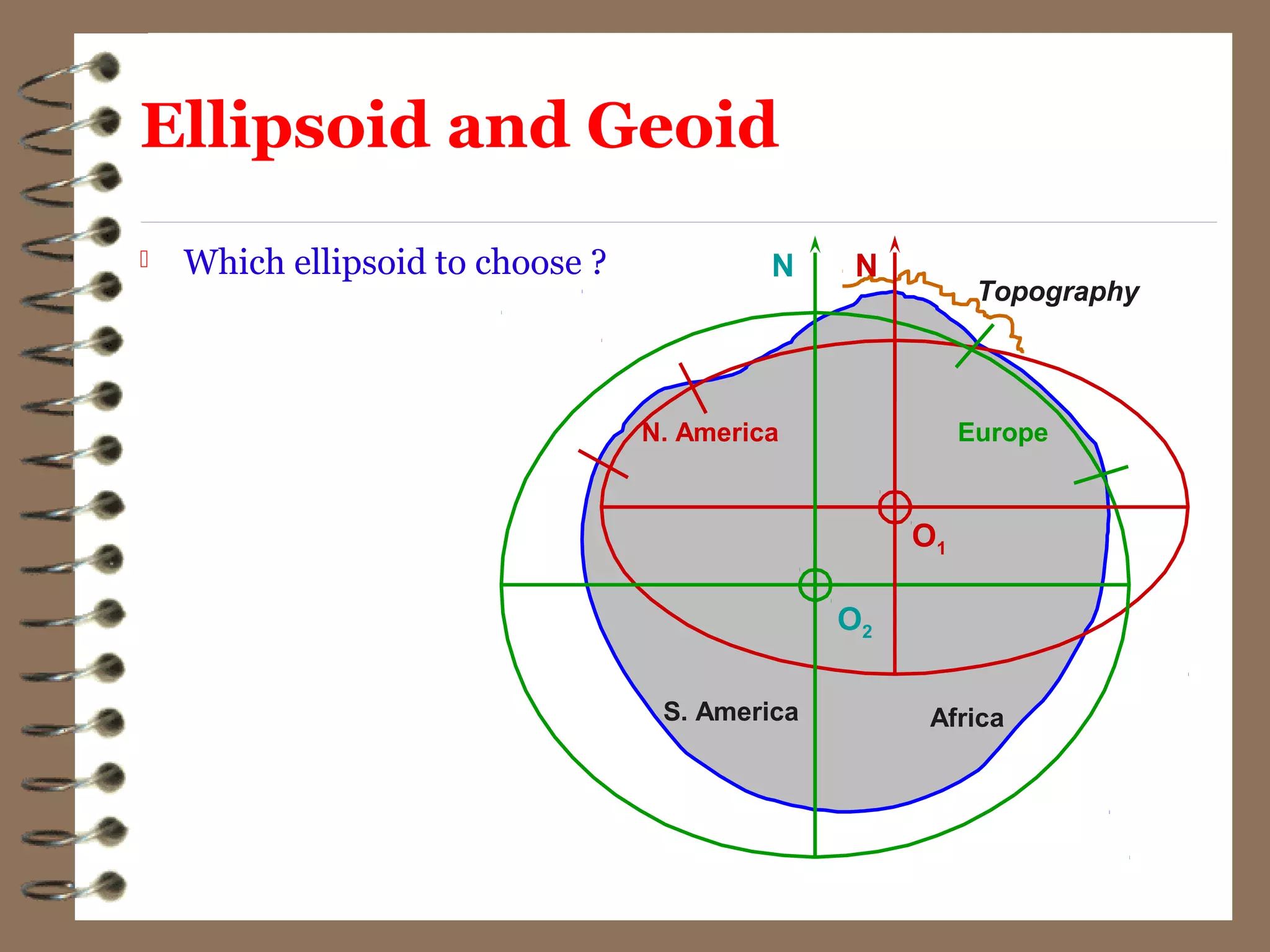
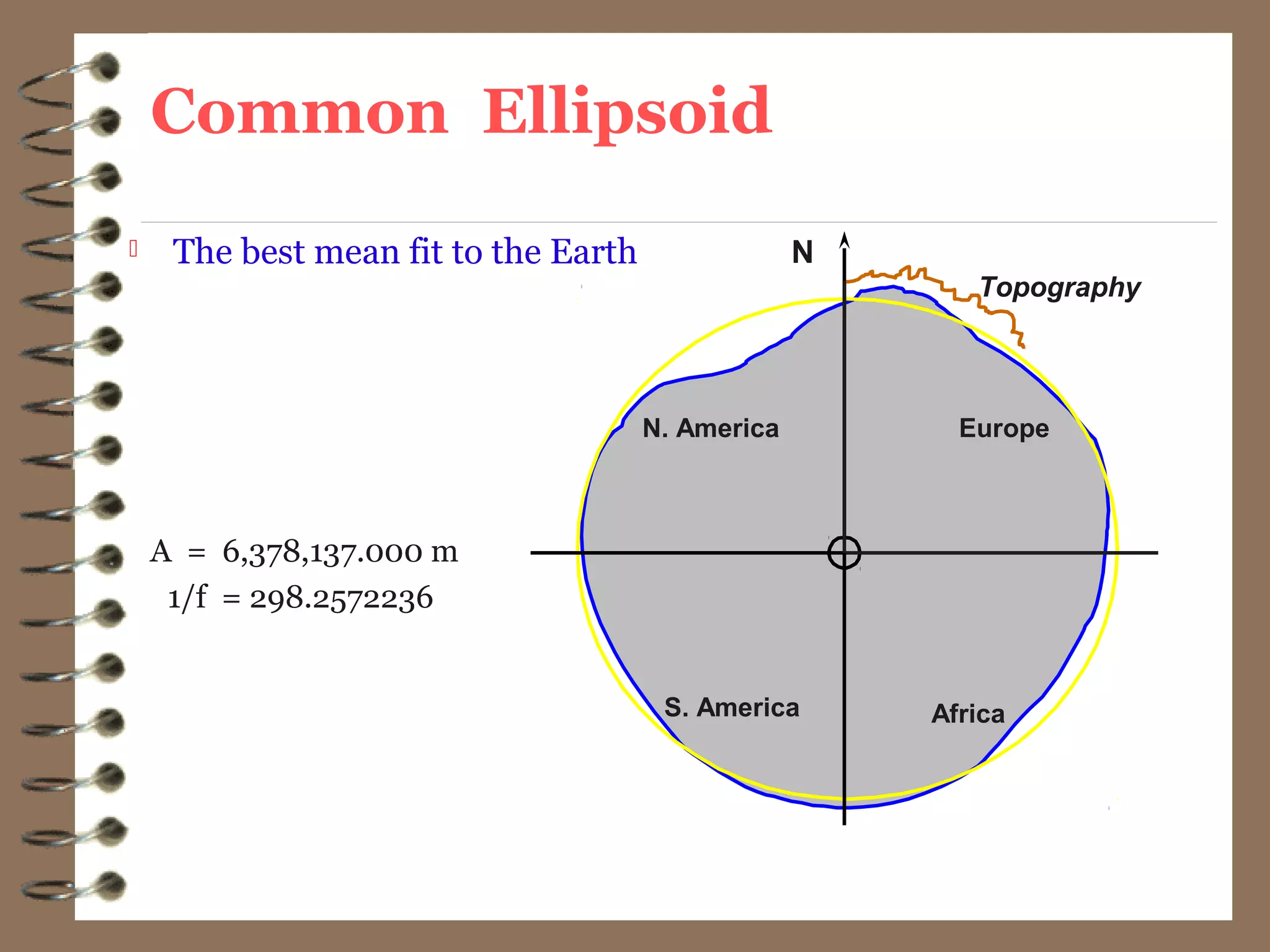
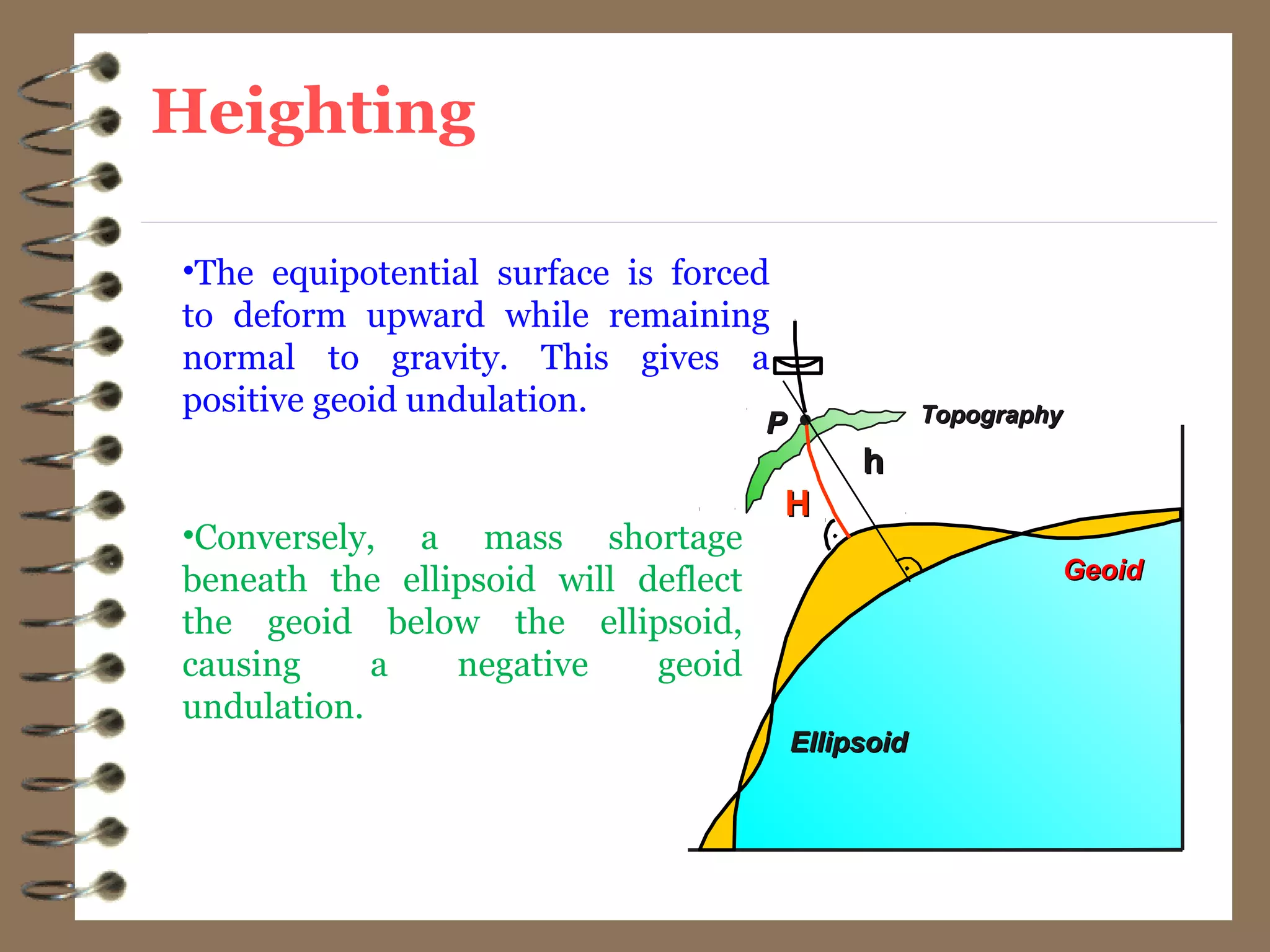
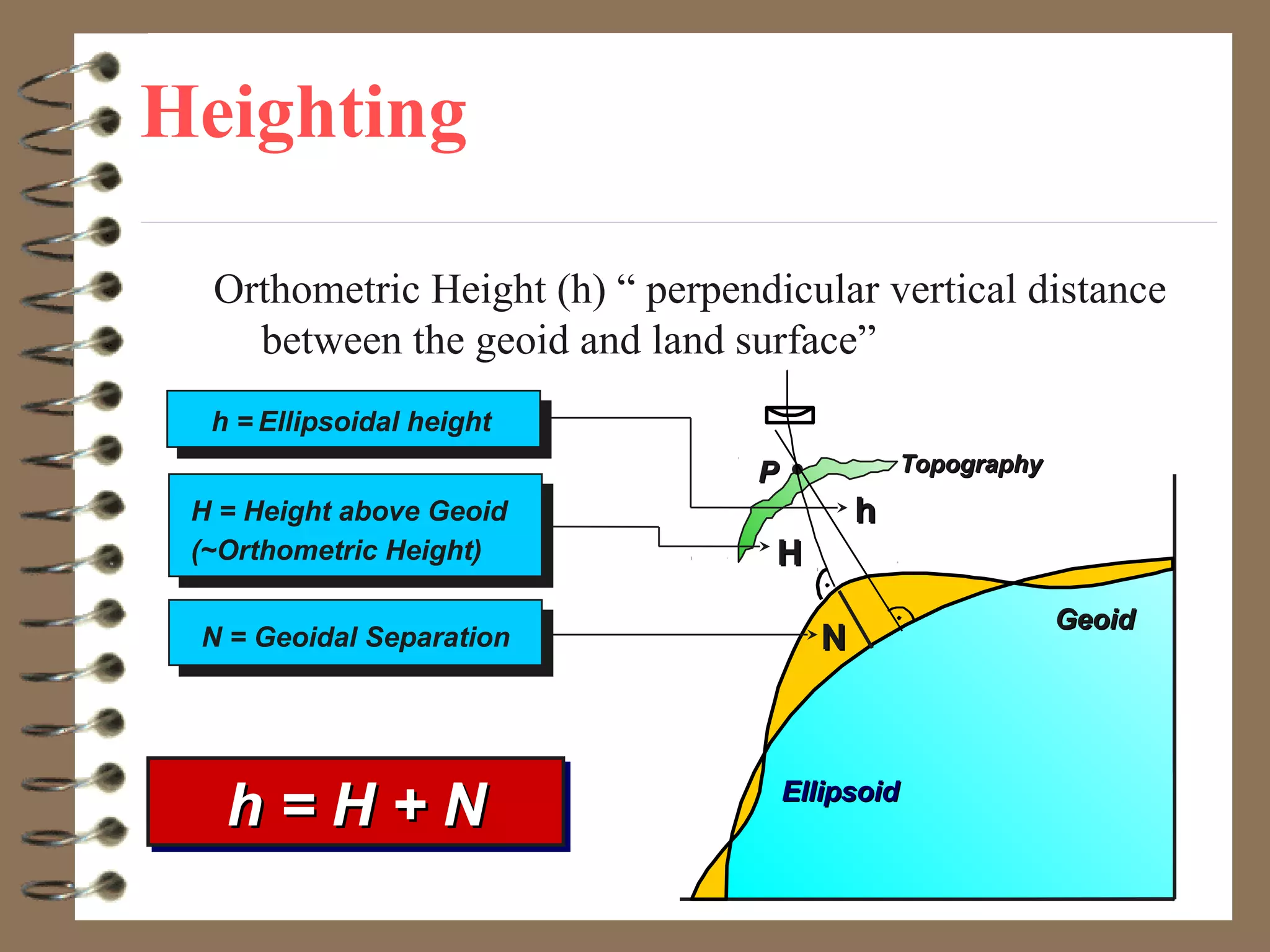
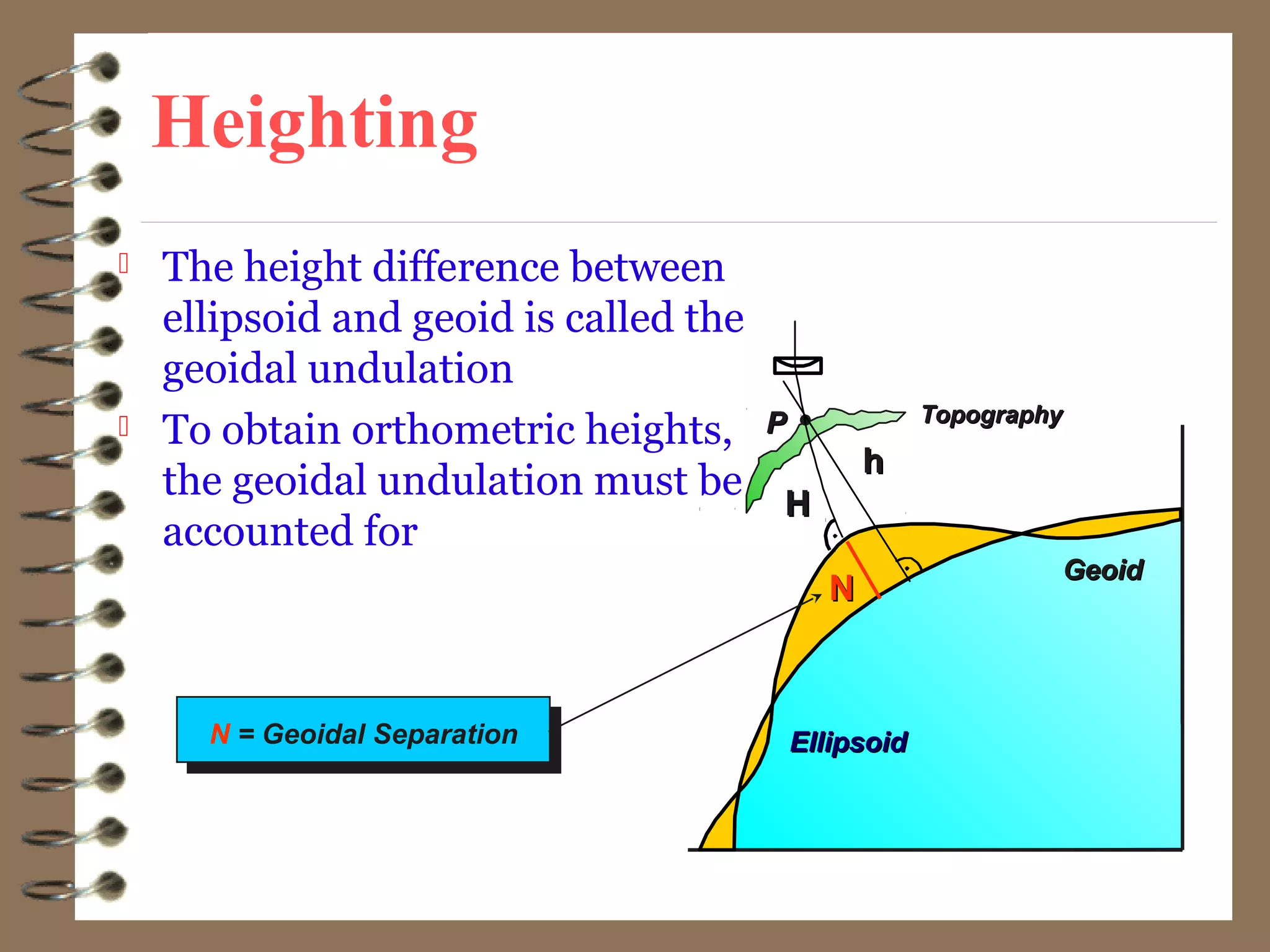
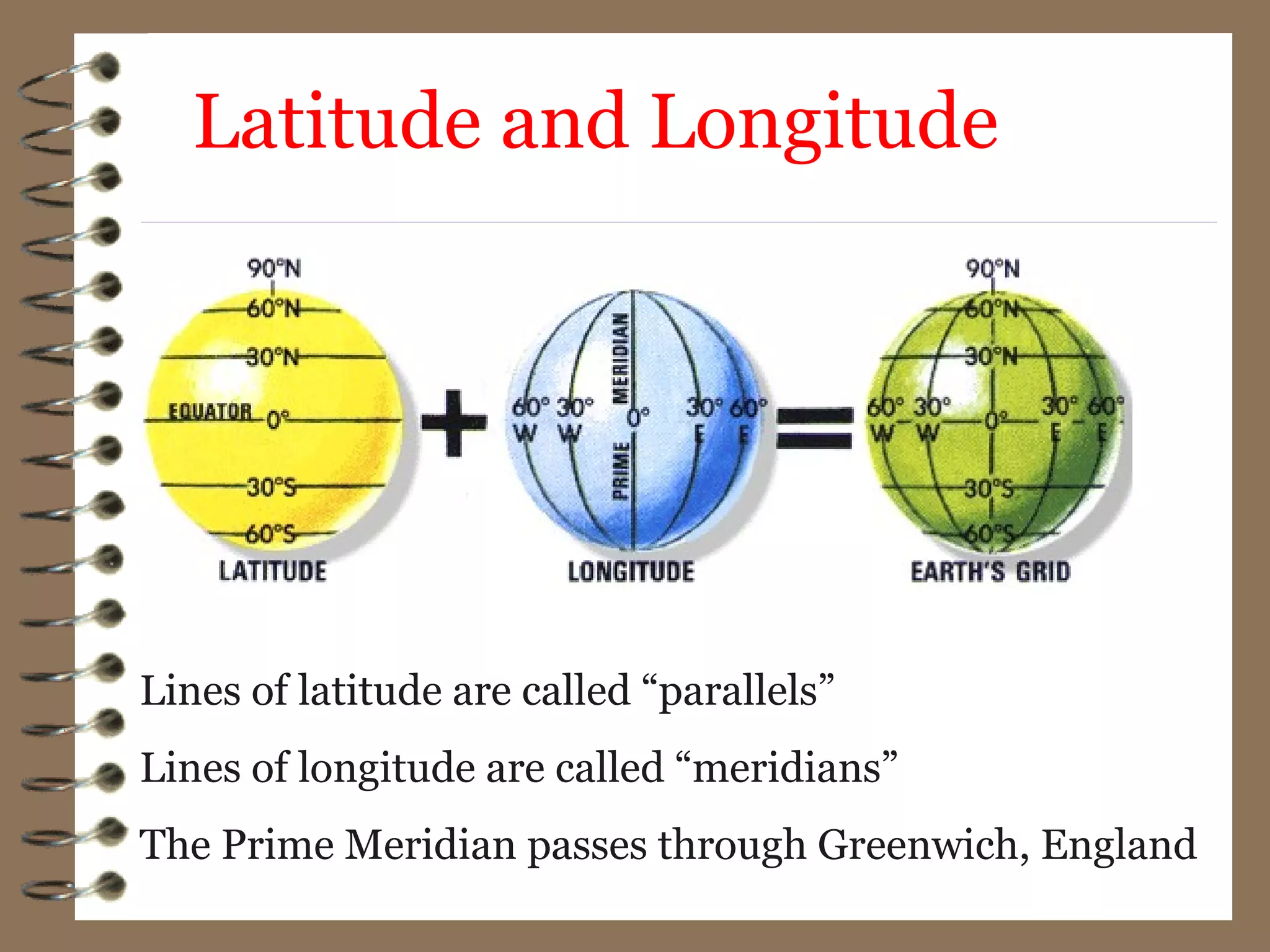
1) Geodesy is the science of measuring and mapping the Earth's surface, including determining its shape, size, and gravity field. 2) Early Greek scholar Eratosthenes used simple observations and geometry to estimate the circumference of Earth to within 1% accuracy over 2000 years ago. 3) While the Earth is approximated as an oblate spheroid, its true shape, called the geoid, is irregular due to density variations underground. Precise positioning and heights require accounting for geoid undulations.

1. Geodesy, GE 202
Kutubuddin ANSARI
kutubuddin.ansari@ikc.edu.tr
Lecture 1, Sep 27, 2016
Basic of Geodesy

2. Geodesy :- Geo - Earth desy - The
study of
“The study of the Earth”
Geodesy is the science of the
measurement and mapping of the earth’s
surface

3. Merriam-Webster:a branch of
applied mathematics concerned with the
determination of the size and shape of
the earth and the exact positions of
points on its surface and with the
description of variations of its gravity
field.

4. • Geometrical geodesy is concerned with describing
locations in terms of geometry. Consequently, coordinate
systems are one of the primary products of geometrical
geodesy.
•Physical geodesy is concerned with determining the
Earth’s gravity field, which is necessary for establishing
heights.
•Satellite geodesy is concerned with using orbiting
satellites to obtain data for geodetic purposes.
Types of Geodesy

5. R
ψ
ΔG
R = ΔG /Ψ
Spherical Model of the Earth

6. Eratosthenes had observed that
on the day of the summer solstice
(20-22 June), the midday sun
shone to the bottom of a well in
the Ancient Egyptian city of
Swenet (known in Greek as
Syene).
Eratosthenes Egypt
about 240 BC
Spherical Model of the Earth

7. Syene
Alexandria
500m
i

8. •He knew that at the same time, the sun was not
directly overhead at Alexandria; instead, it cast a
shadow with the vertical equal to 1/50th of a circle (7°
12').
•He also knew that Alexandria and Syene were 500
miles apart
•To these observations, Eratosthenes concluded that
the circumference of the earth was 50 x 500 miles, or
25000 miles.
Spherical Model of the Earth

9. •The accepted value along the equator is 24,902 miles,
but, if you measure the earth through the poles the value
is 24,860 miles
•He was within 1% of today’s accepted value
•Eratosthenes' conclusions were highly regarded at the
time, and his estimate of the Earth’s size was accepted
for hundreds of years afterwards.
Spherical Model of the Earth

10. How Do We Define the Shape
of the Earth?
We think of the
earth as a sphere
It is actually a spheroid,
slightly larger in radius
at the equator than at the
poles

11. The Ellipsoid
 An ellipse is a mathematical
figure which is defined by
Semi-Major Axis (a)
and
Semi-Minor Axis (b)
or
Flattening (f) = (a - b)/a
 It is a simple geometrical
surface
 Cannot be sensed by
instruments
b
a

12. Ellipsoid or Spheroid
O
X
Z
Ya a
b
Rotational axis
Rotate an ellipse around an axis

13. Selection of the Spheroid is what
determines the size of the Earth

14. The Real Earth
(The Geoid)

15. EuropeN. America
S. America Africa
Topography
An ellipsoidal-earth model is
no longer tenable at a high
level of accuracy. The
deviation of the physical
measurements refer from the
ellipsoidal model can no
longer be ignored.
The geoid anomaly is the
difference between the geoid
surface and a reference
ellipsoid
The Real Earth (Geoid)

16. What is the Geoid?
• “The equipotential
surface of the Earth’s
gravity field which
best fits, in the least
squares sense, global
mean sea level.”
• Can’t see the surface
or measure it directly.
• Modeled from gravity
data.

17. Ellipsoid and Geoid
 Ellipsoid
• Simple Mathematical Definition
• Described by Two Parameters
• Cannot be 'Sensed' by Instruments
 Geoid
• Complicated Physical Definition
• Described by Infinite Number of
Parameters
• Can be 'Sensed' by Instruments

18. Earth surface
EllipsoidSea surface
Geoid
Since the Geoid varies due to local anomalies, we must
approximate it with a ellipsoid
Ellipsoid and Geoid

19. O1
EuropeN. America
S. America Africa
Topography
N
Ellipsoid and Geoid

20.  Which ellipsoid to choose ?
O2
O1
EuropeN. America
S. America Africa
N
Topography
N
Ellipsoid and Geoid

21. Common Ellipsoid
 The best mean fit to the Earth
EuropeN. America
S. America Africa
N
Topography
A = 6,378,137.000 m
1/f = 298.2572236

22. Unfortunately, the density of the earth’s crust is not uniformly the
same. Heavy rock, such as an iron ore deposit, will have a stronger
attraction than lighter materials. Therefore, the geoid (or any
equipotential surface) will not be a simple mathematical surface.
Ellipsoid and Geoid Heights

23. Heighting
•The equipotential surface is forced
to deform upward while remaining
normal to gravity. This gives a
positive geoid undulation.
•Conversely, a mass shortage
beneath the ellipsoid will deflect
the geoid below the ellipsoid,
causing a negative geoid
undulation.
EllipsoidEllipsoid
PP
HH
GeoidGeoid
hh
TopographyTopography

24. h = H + Nh = H + Nh = H + Nh = H + N EllipsoidEllipsoid
hh
PP TopographyTopography
HH
GeoidGeoid
NNN = Geoidal Separation
H = Height above Geoid
(~Orthometric Height)
h = Ellipsoidal height
Heighting
Orthometric Height (h) “ perpendicular vertical distance
between the geoid and land surface”

25. Heighting
 The height difference between
ellipsoid and geoid is called the
geoidal undulation
 To obtain orthometric heights,
the geoidal undulation must be
accounted for
EllipsoidEllipsoid
PP
HH
GeoidGeoid
NN
N = Geoidal Separation
hh
TopographyTopography

26. Latitude and Longitude
Lines of latitude are called “parallels”
Lines of longitude are called “meridians”
The Prime Meridian passes through Greenwich, England

27. Latitude and Longitude in N. America
90 W
120 W 60 W
30 N
0 N
60 N

28. Length on Meridians and Parallels
0 N
30 N
∆φ
Re
Re
R
R
A
B
C
∆λ
(Lat, Long) = (φ, λ)
Length on a Meridian:
AB = Re ∆φ
(same for all latitudes)
Length on a Parallel:
CD = R ∆λ = Re ∆λ Cos φ
(varies with latitude)
D

29. Any set of numbers,
usually in sets of
two or three, used to
determine location
relative to other
locations in two or
three dimensions
Coordinate systems

30. Global Cartesian Coordinates (x,y,z)
O
X
Z
Y
Greenwich
Meridian
Equator
•
•A system for the whole
earth
•Non manageable and
difficult to relate to other
locations when translated
to two dimensions
•The z-coordinate is
defined as geometrically

31. Geographic Coordinates (φ, λ, z)
• Latitude (φ) and Longitude (λ) defined using an
ellipsoid, an ellipse rotated about an axis
• Elevation (z) defined using geoid, a surface of
constant gravitational potential

32. Origin of Geographic Coordinates
(0,0)
Equator
Prime Meridian

33. Coordinate System
(φo,λo)
(xo,yo)
X
Y
Origin
A planar coordinate system is defined by a pair
of orthogonal (x,y) axes drawn through an origin

34. (φ, λ) (x, y)
Map Projection
Coordinate System