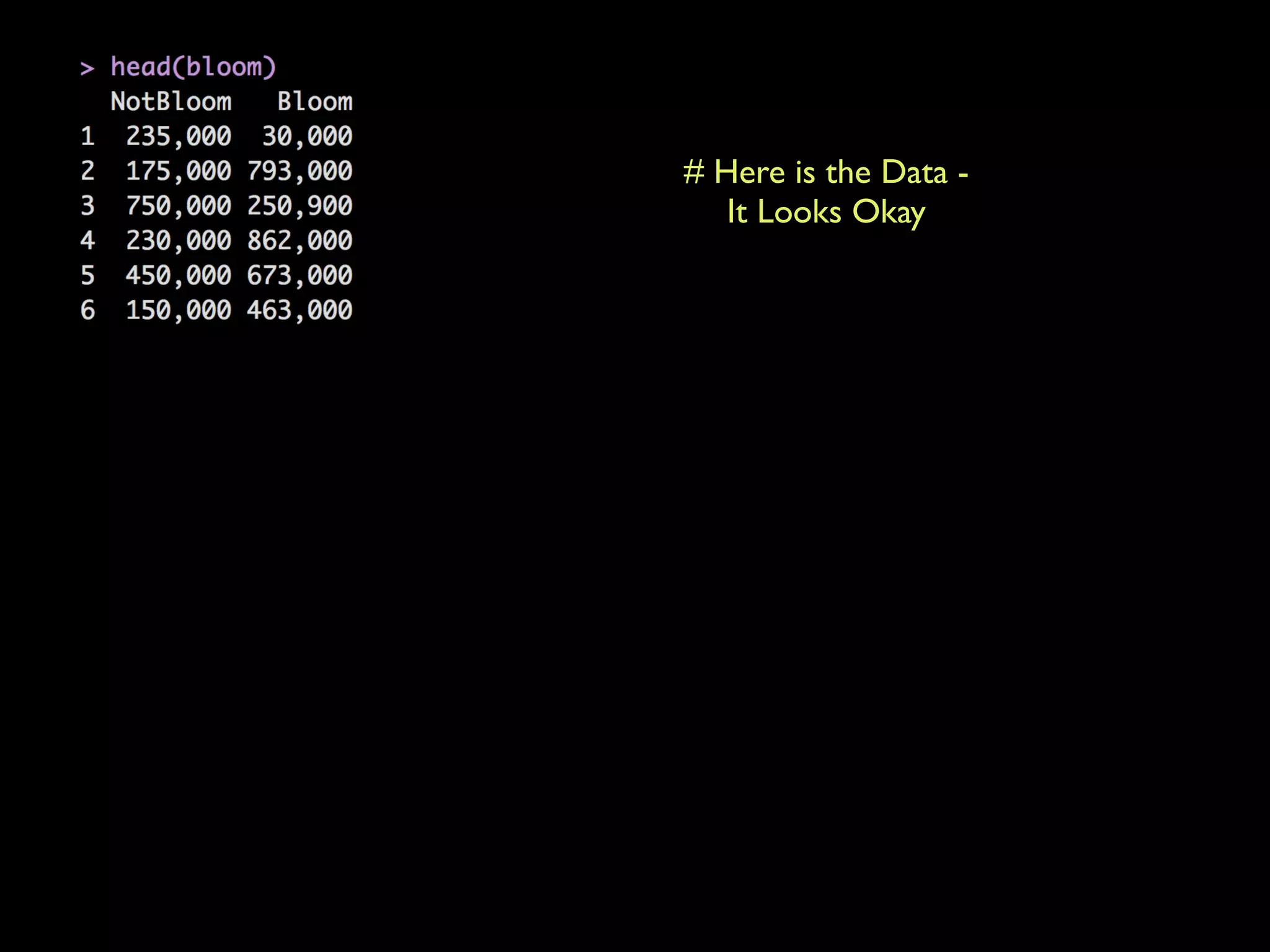
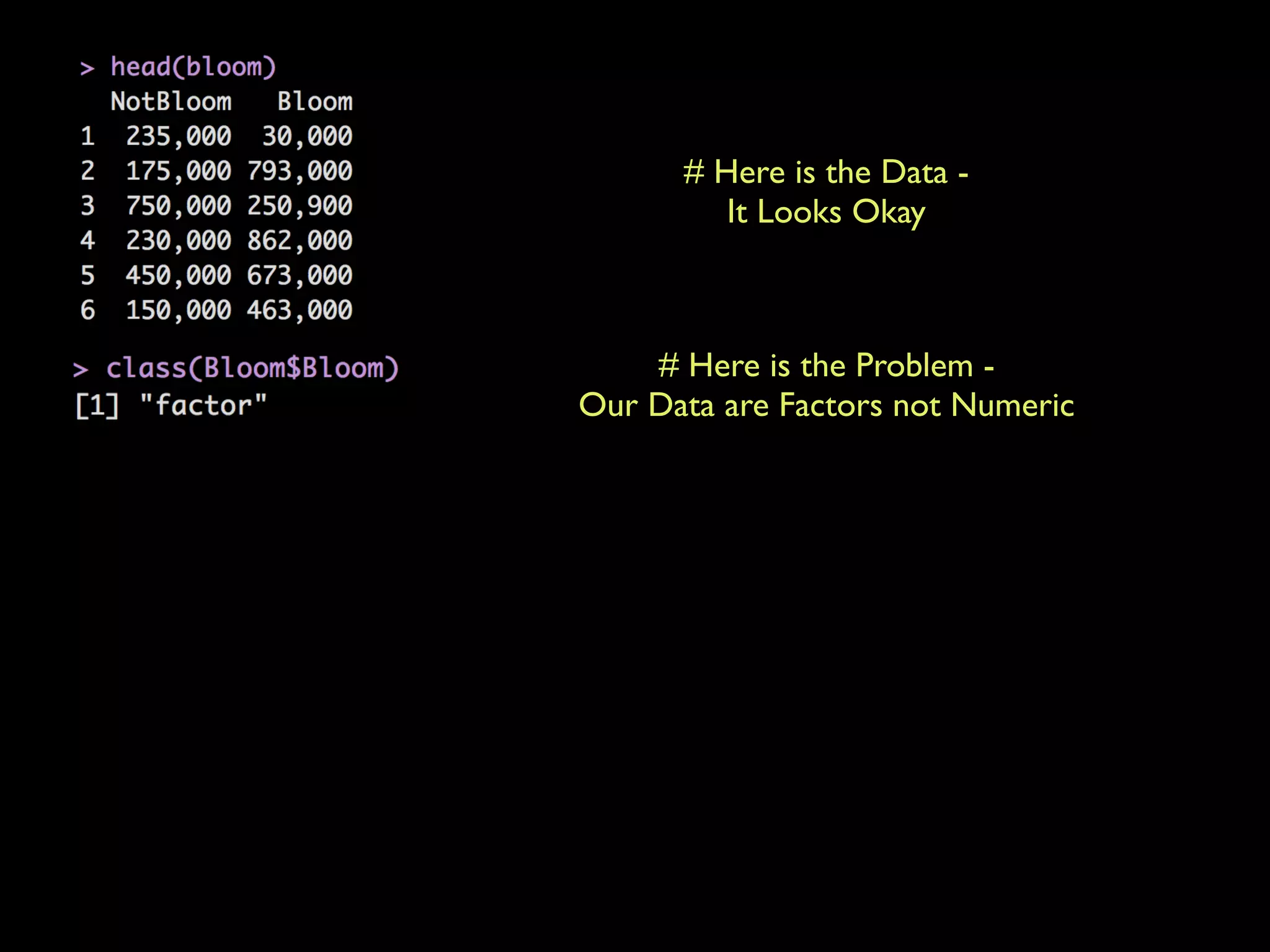
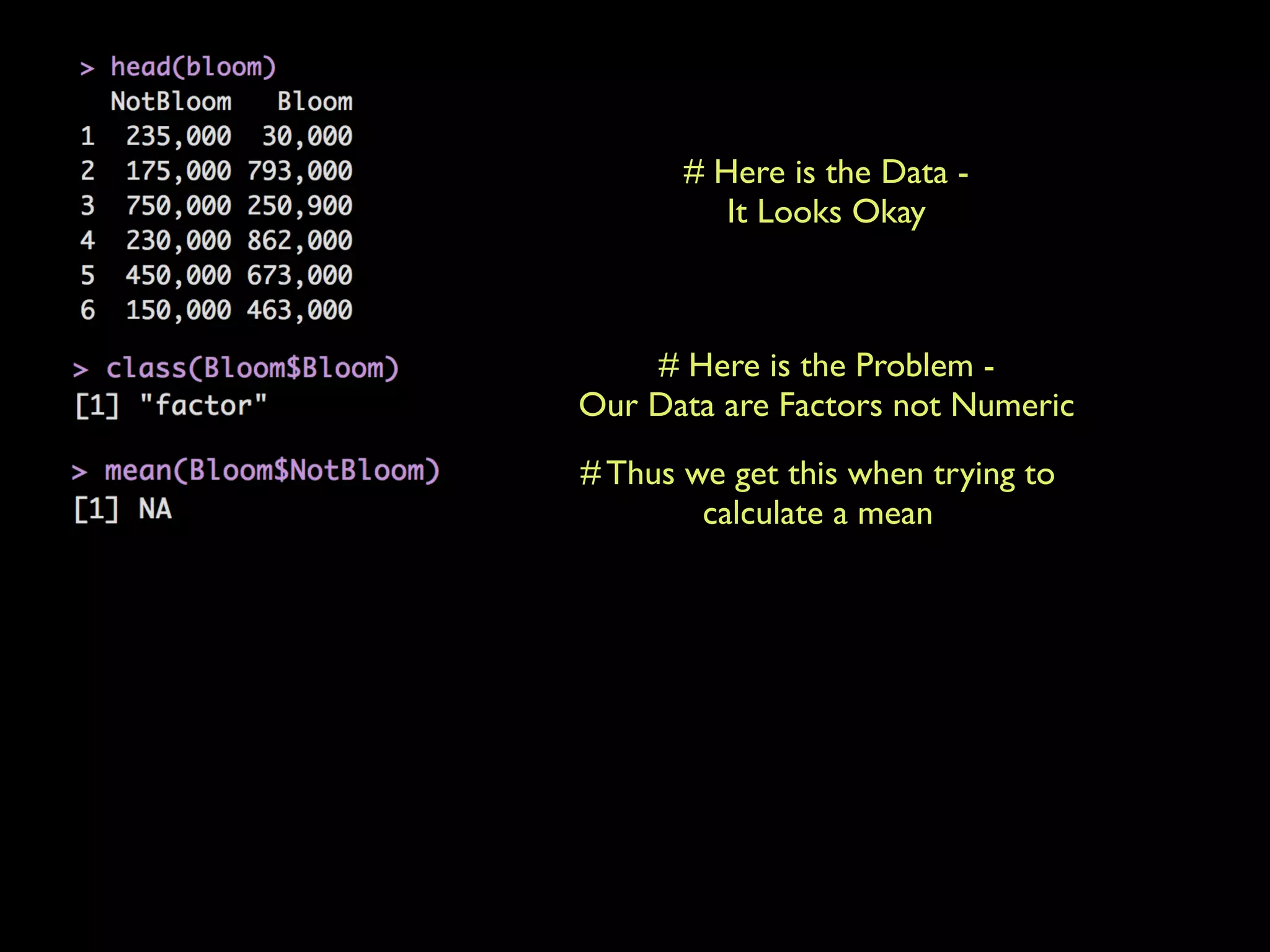
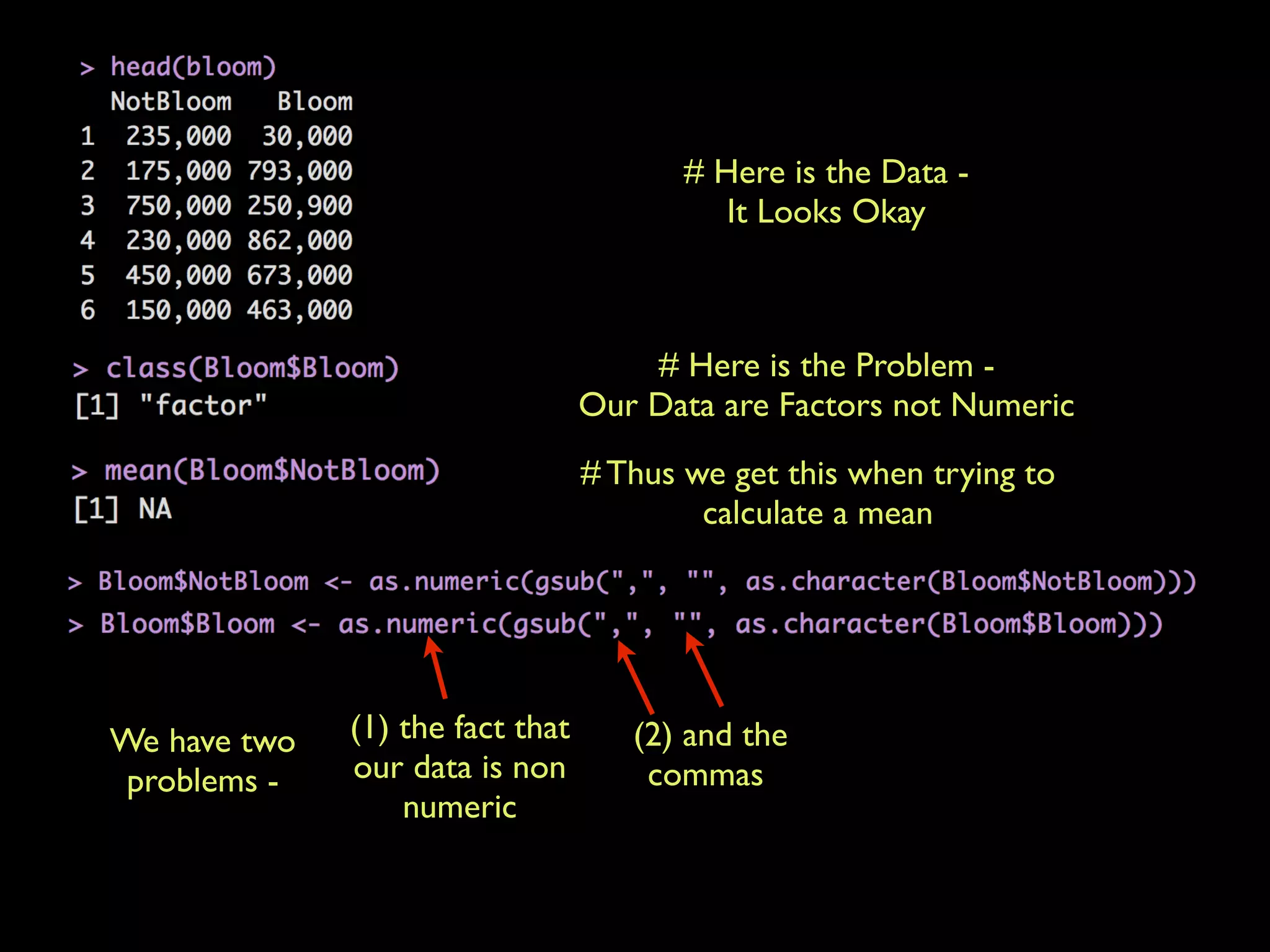
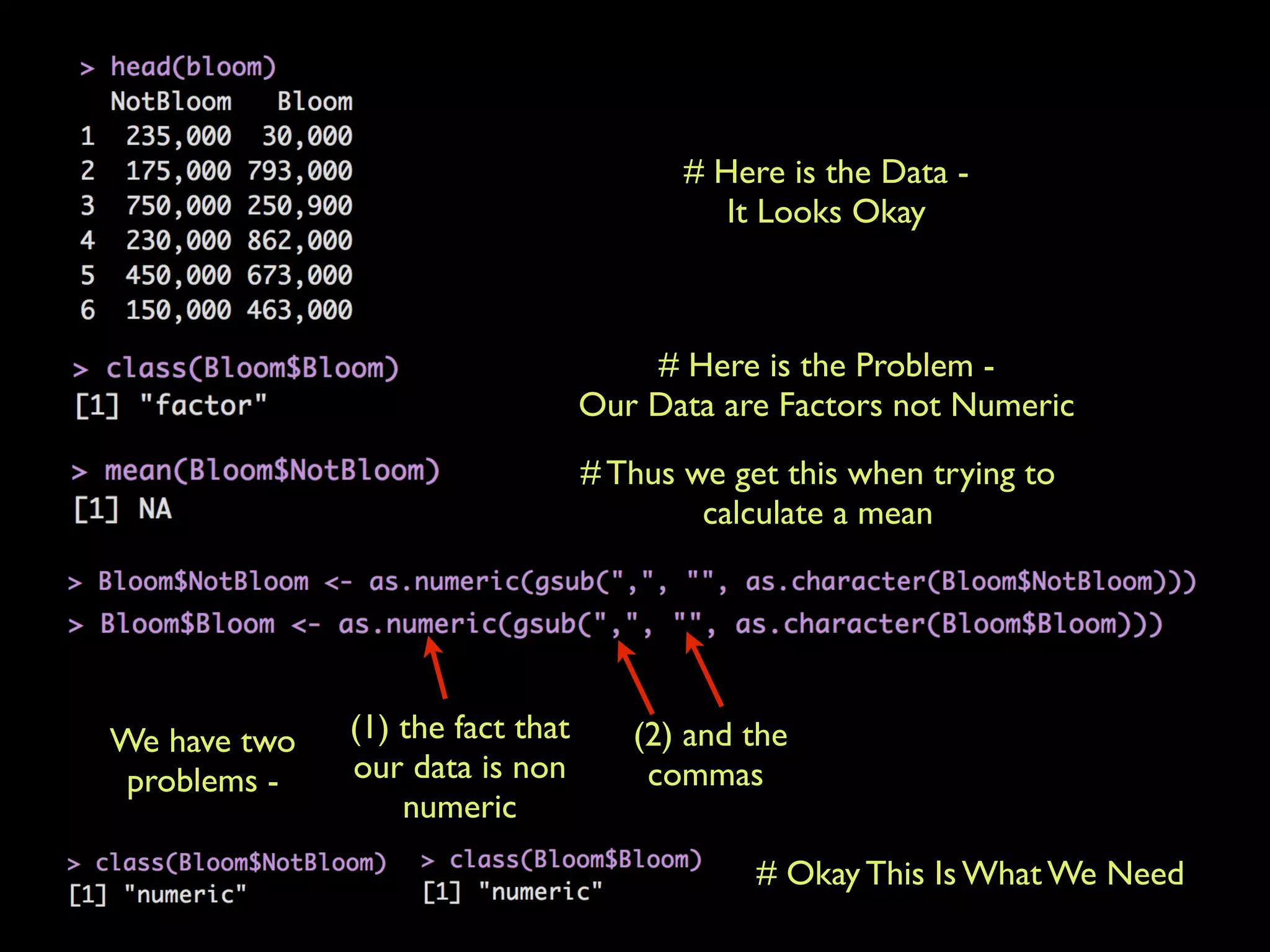
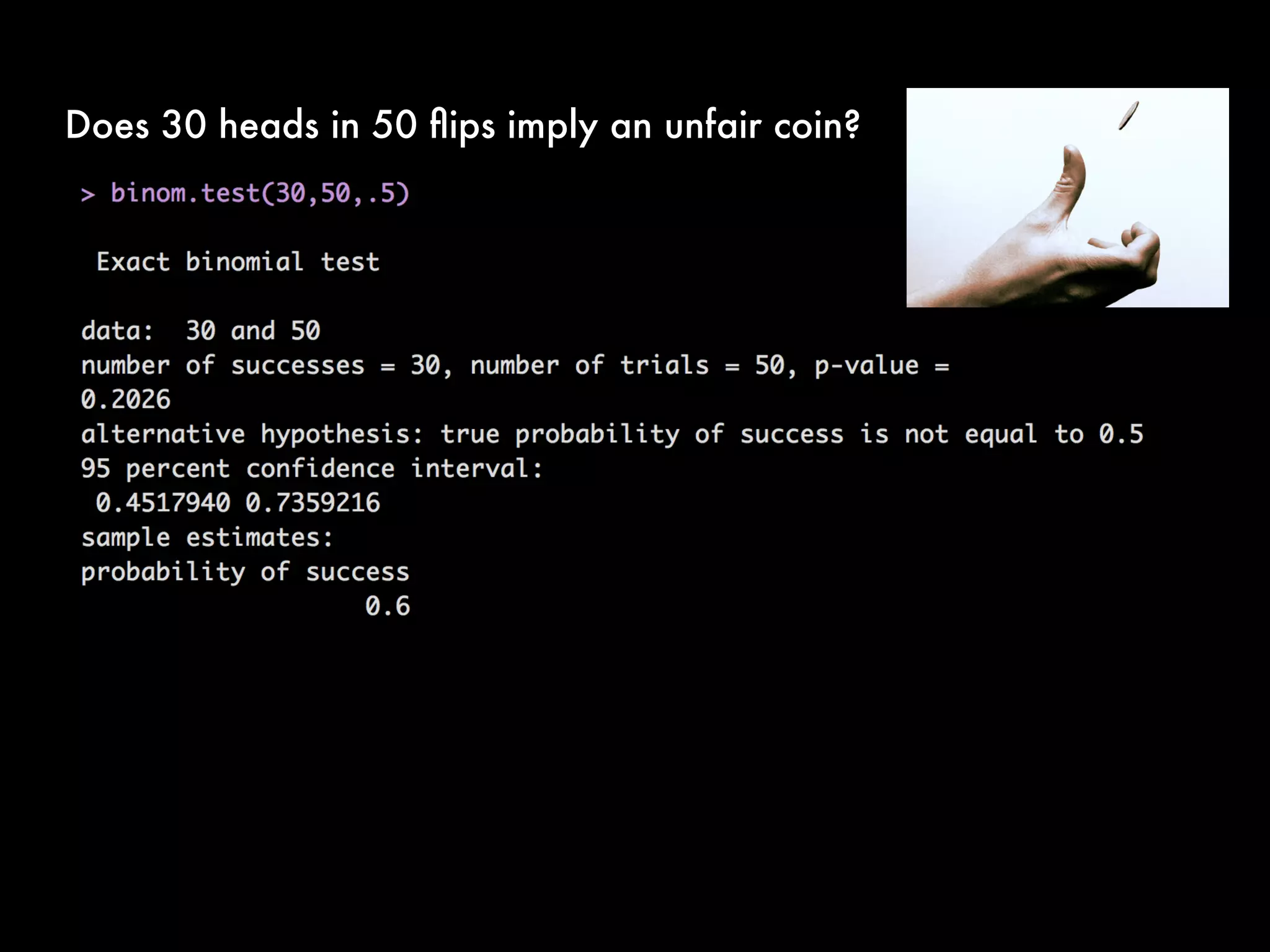
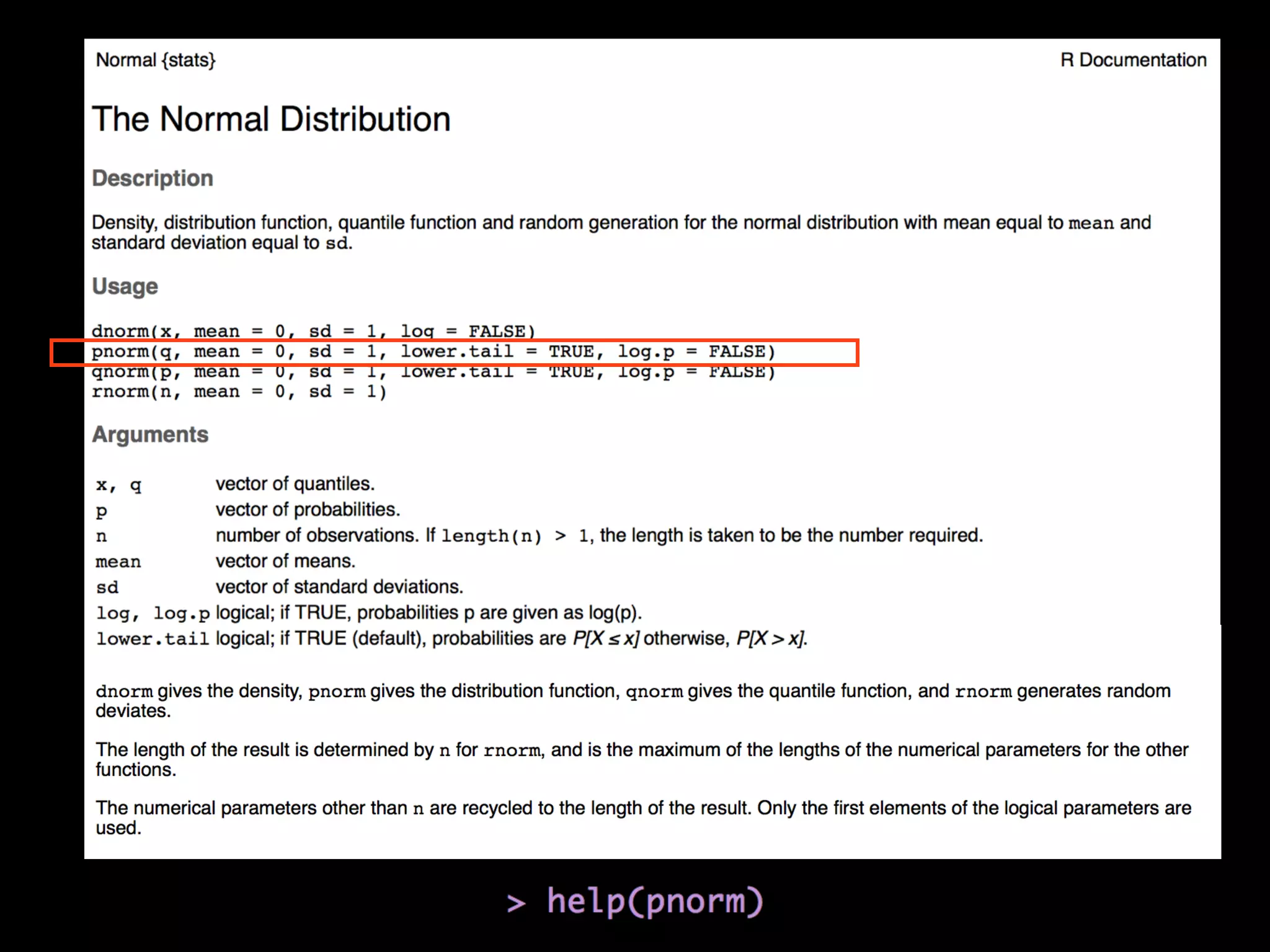
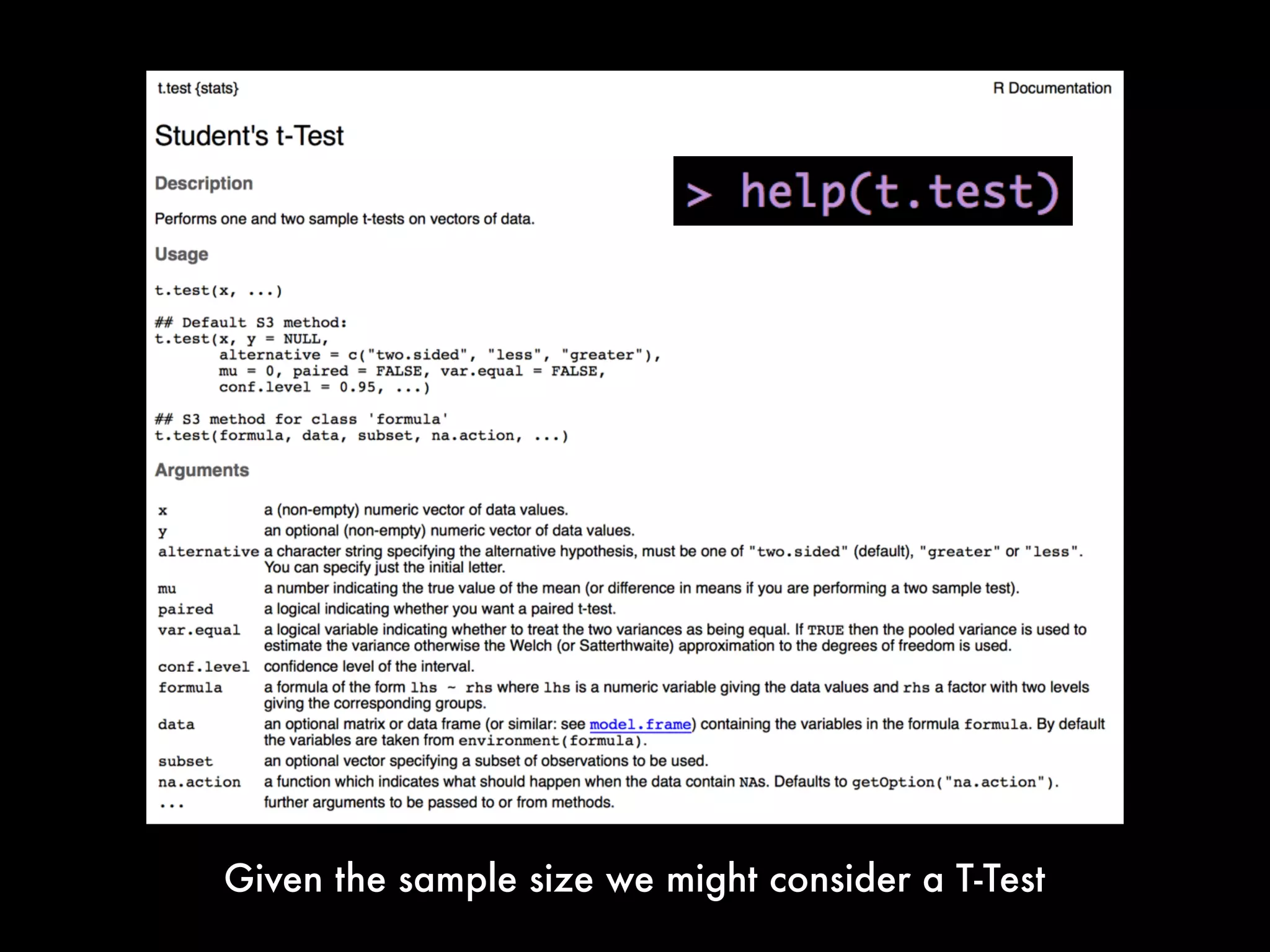
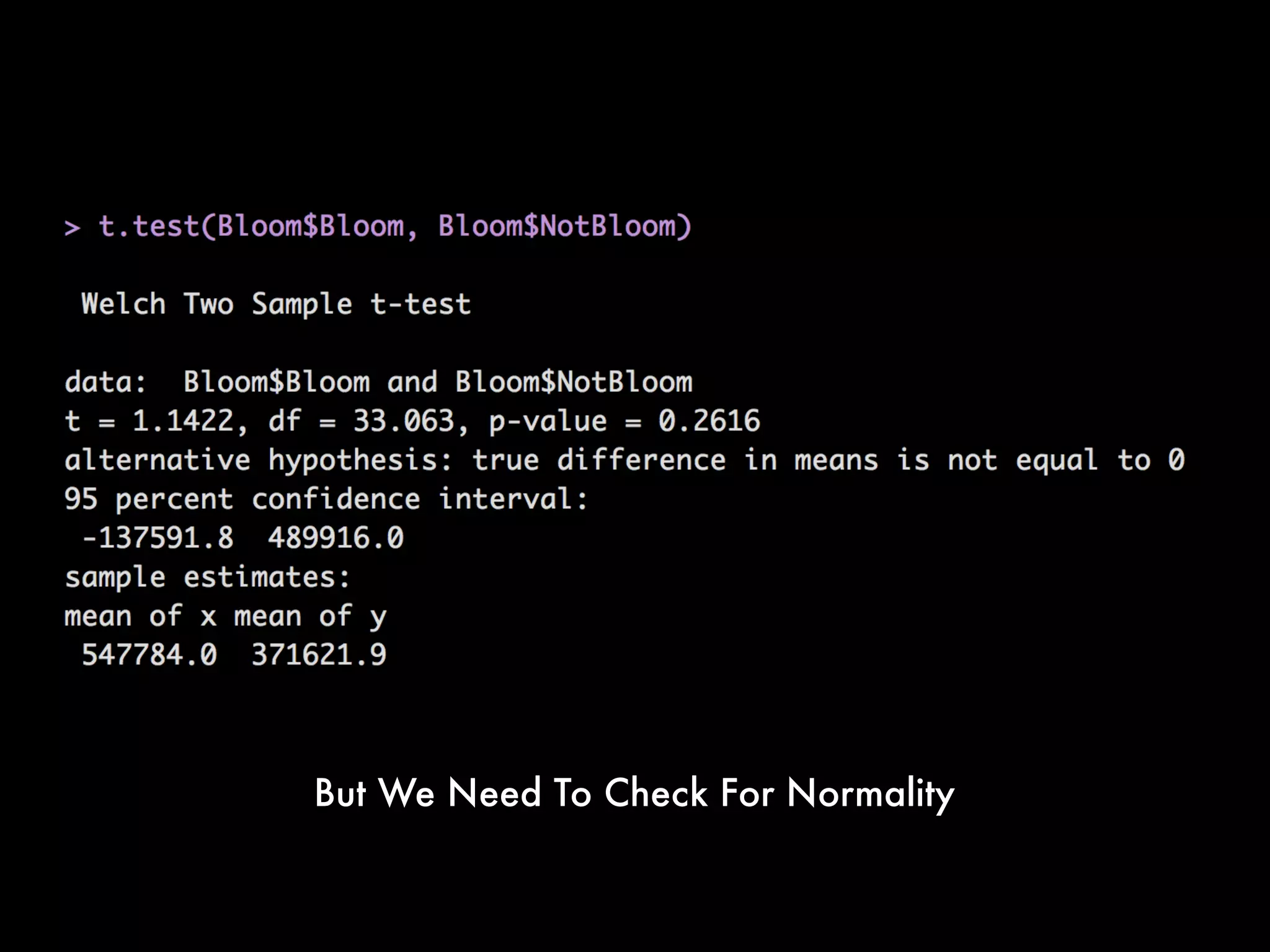
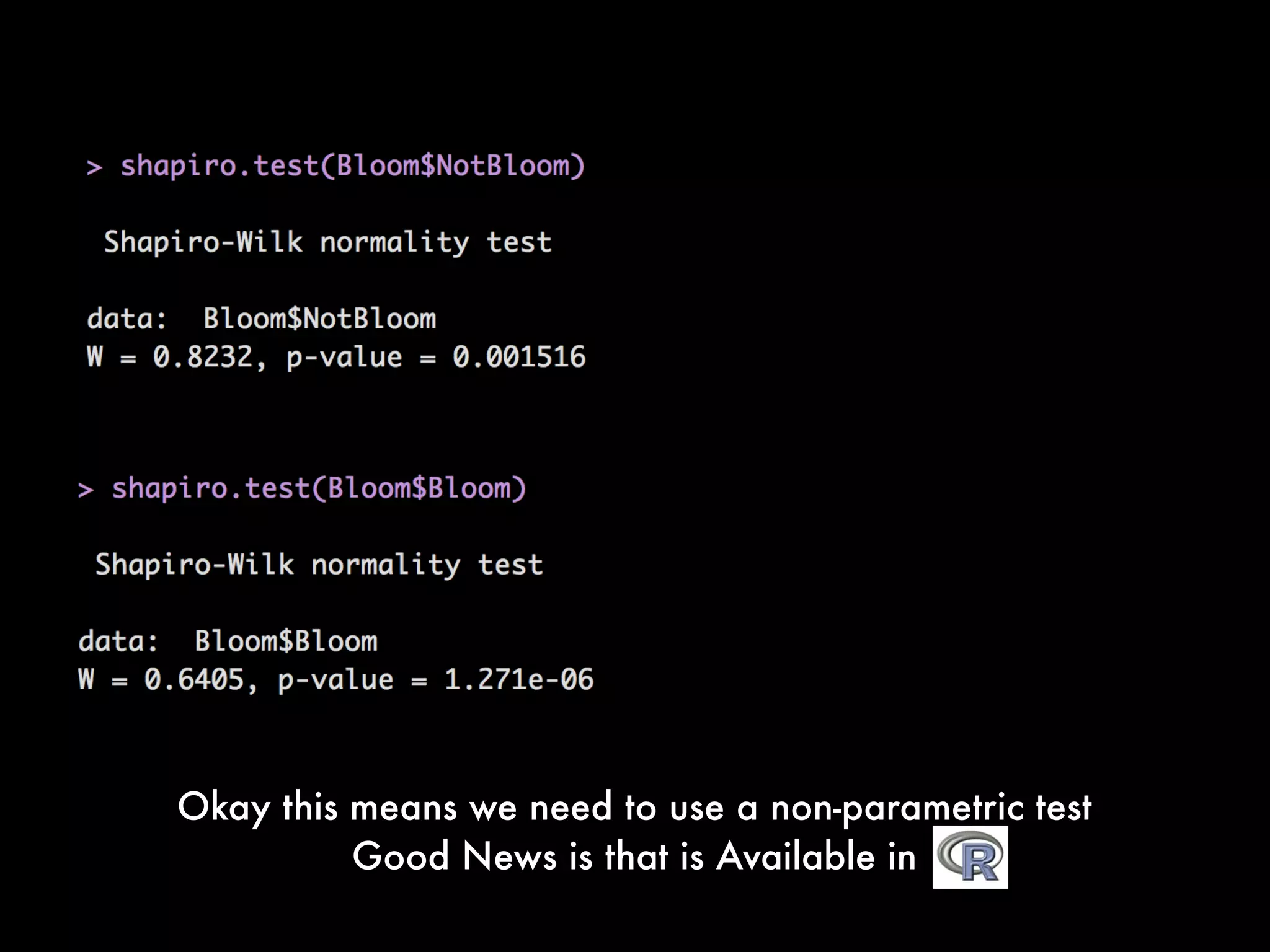
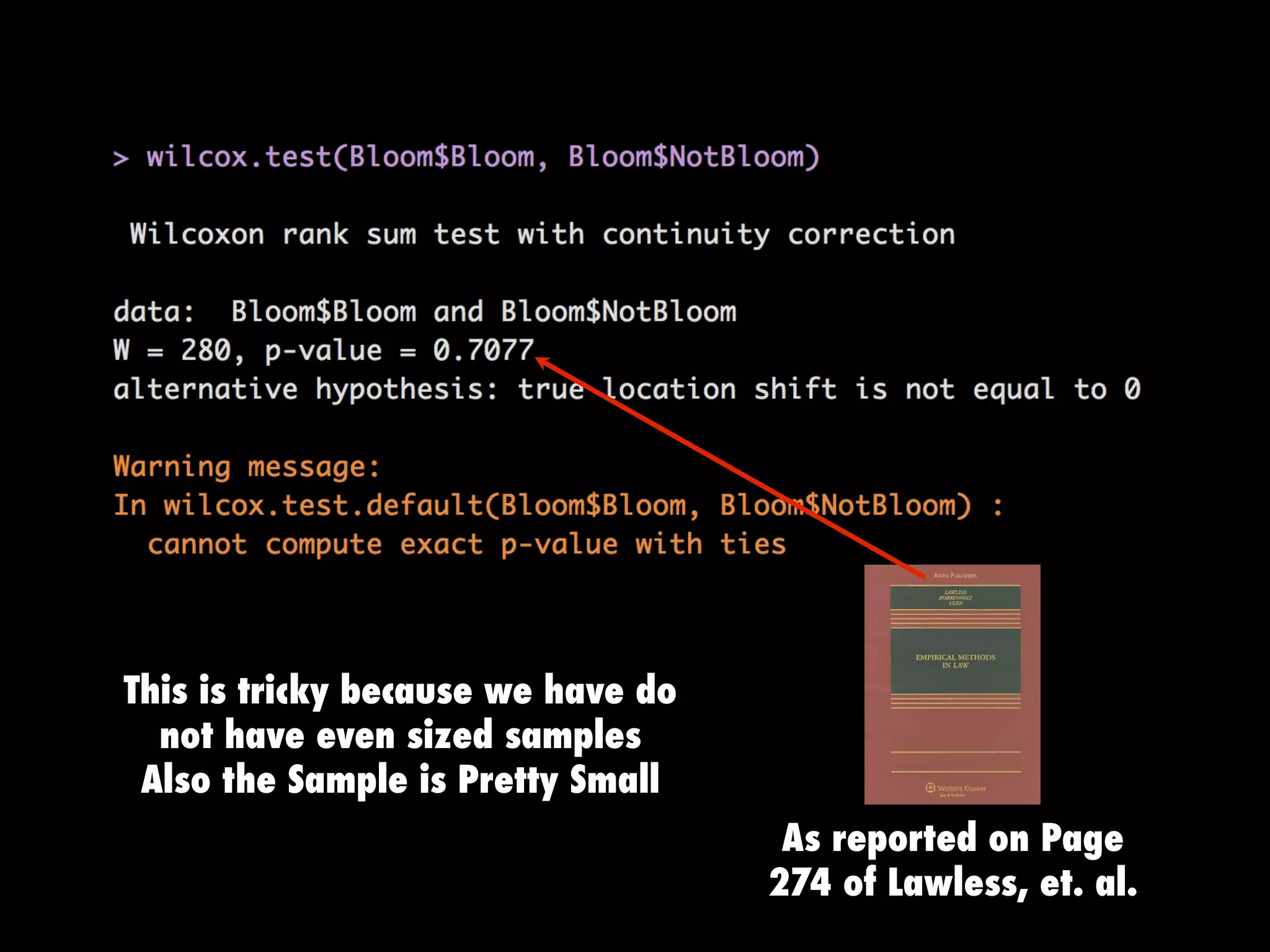
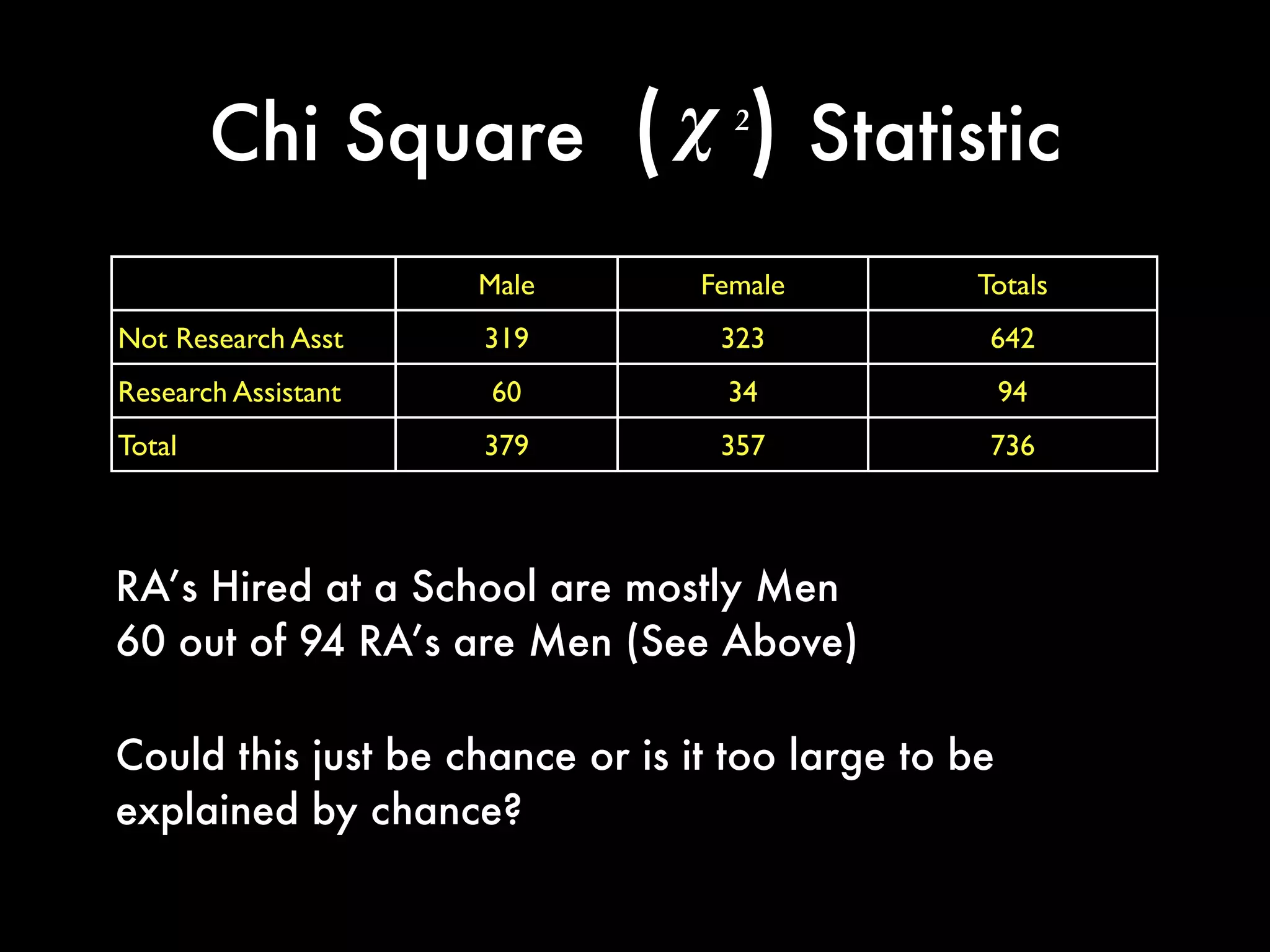
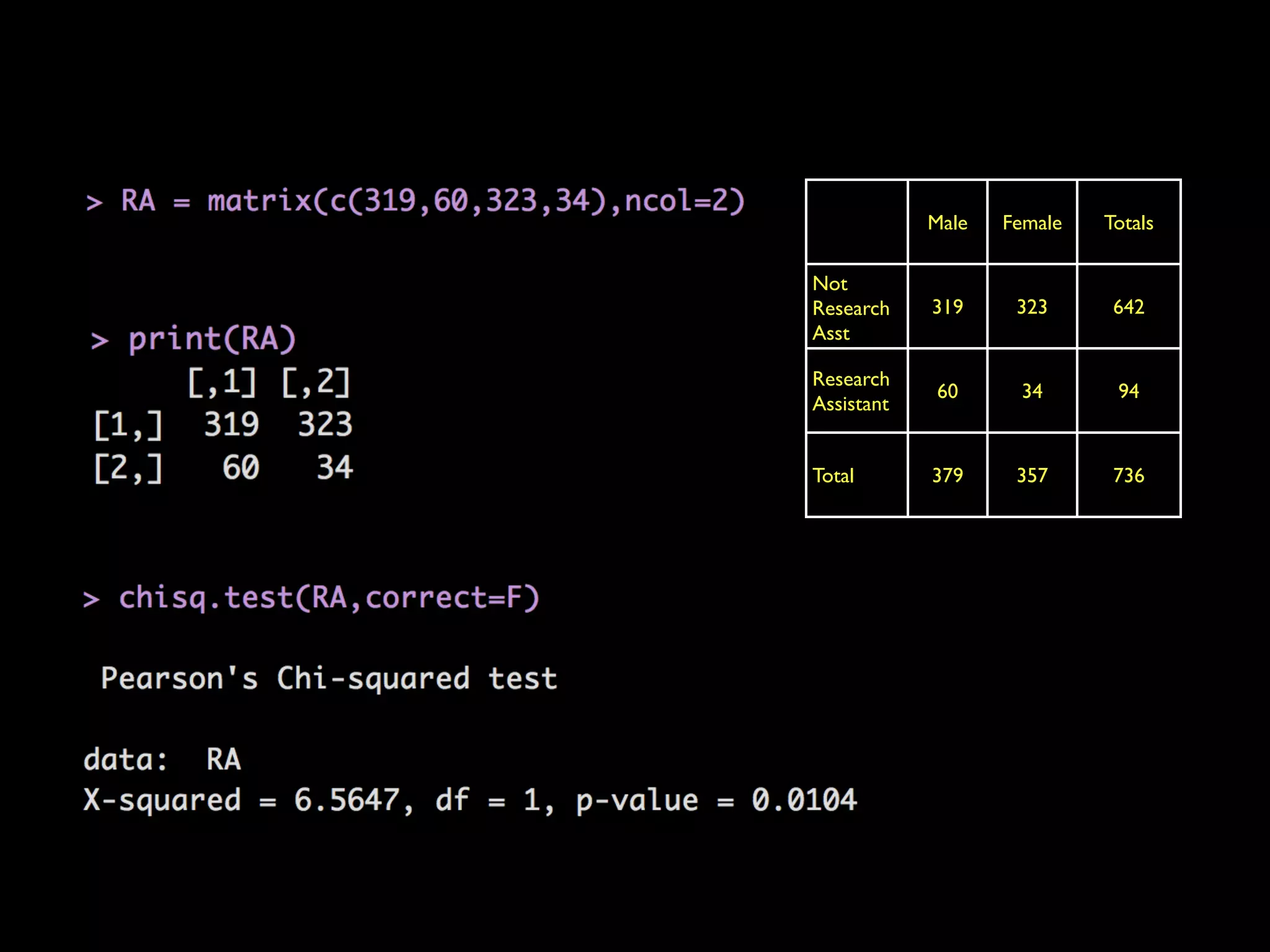
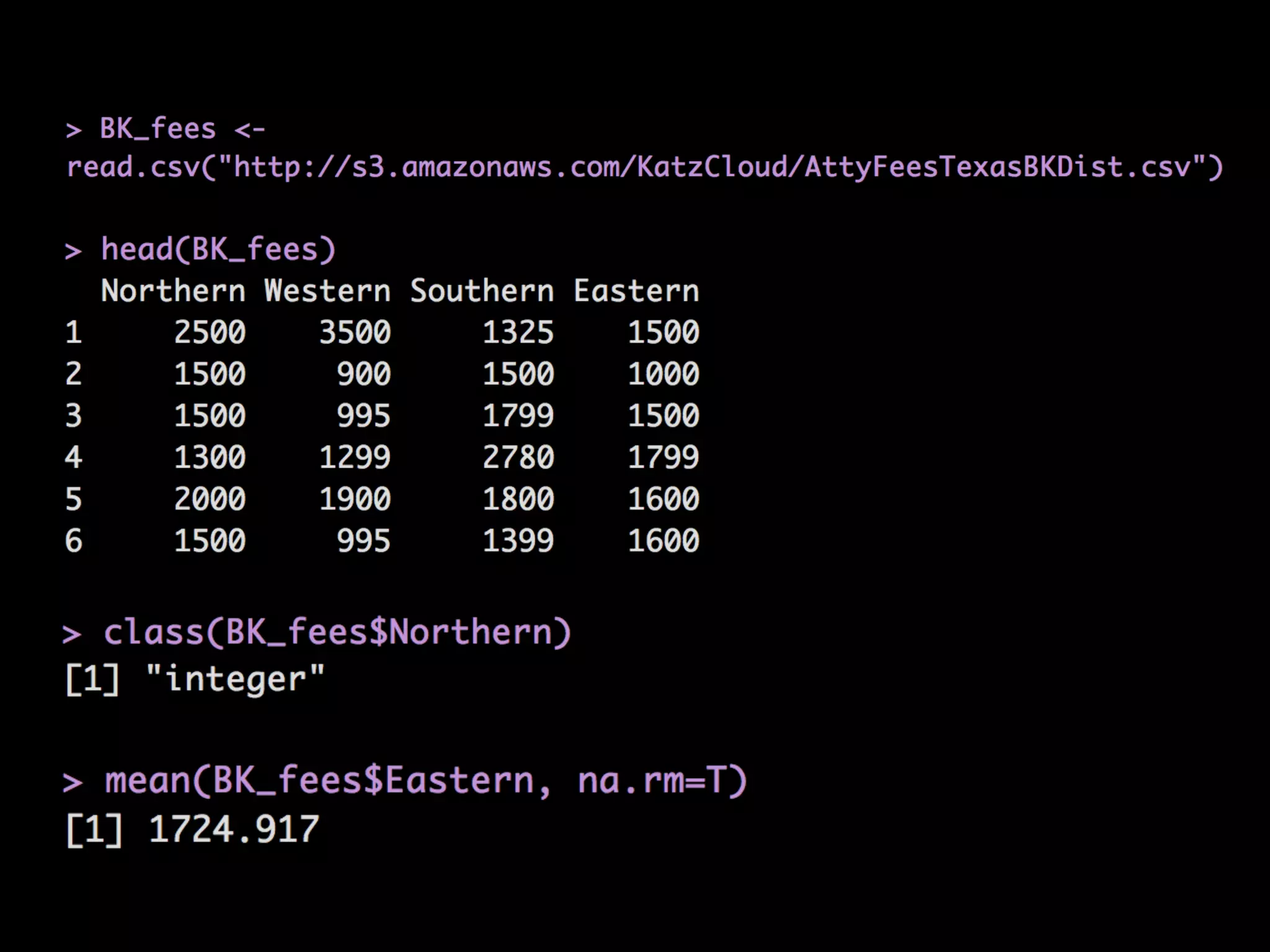
This document provides an overview of statistical tests and calculations using R. It discusses loading and cleaning a dataset, doing basic calculations, and running statistical tests like the binomial distribution, normal distribution, hypothesis testing, chi-squared test, and F test. Examples are provided for each type of analysis, including the R code and interpretation. The goal is to demonstrate how to use R to analyze datasets and evaluate various statistical hypotheses.

1. Quantitative
Methods
for
Lawyers
Statistical Tests Using R
R Boot Camp - Part 2
Class #15
@ computational
computationallegalstudies.com
professor daniel martin katz danielmartinkatz.com
lexpredict.com slideshare.net/DanielKatz

2. My Challenge to You
Use R to
Download and
Clean this Simple
DataSet

3. https://s3.amazonaws.com/KatzCloud/Bloom.csv
Load into R and Do
Some Basic Calculations

4. Load into R and Do
Some Basic Calculations
# Just Remember that R does not Handle https://

5. Load into R and Do
Some Basic Calculations
# Just Remember that R does not Handle https://
# Okay We Are Now Loaded

6. # Here is the Data -
It Looks Okay

7. # Here is the Data -
It Looks Okay
# Here is the Problem -
Our Data are Factors not Numeric

8. # Here is the Data -
It Looks Okay
# Here is the Problem -
Our Data are Factors not Numeric
# Thus we get this when trying to
calculate a mean

9. # Here is the Data -
It Looks Okay
# Here is the Problem -
Our Data are Factors not Numeric
# Thus we get this when trying to
calculate a mean
We have two
problems -
(1) the fact that
our data is non
numeric
(2) and the
commas

10. # Here is the Data -
It Looks Okay
# Here is the Problem -
Our Data are Factors not Numeric
# Thus we get this when trying to
calculate a mean
# Okay This Is What We Need
We have two
problems -
(1) the fact that
our data is non
numeric
(2) and the
commas

11. Okay Lets Do Some
Basic Calculations

12. Okay Lets Do Some
Basic Calculations
# Okay We Are All Set

13. Okay Lets See How
to Use R
to Run Some of the
Calculations that we
have already seen in
this class

14. The Binomial
Distribution

15. Binomial Distribution
“A binomial experiment (also known as a Bernoulli trial) is a
statistical experiment that has the following properties:
The experiment consists of n repeated trials.
Each trial can result in just two possible outcomes.
The probability of success, denoted by P, is the
same on every trial.
The trials are independent”

16. Example: Coin Flip
Nostradamus
Predicting Coin Flips -
Does you Friend Have the General Ability to
Actually Predict Coin Flips?
How Would You Evaluate This Proposition?
How Many Predictions Would Your Friend Have to Get Right
For You To Believe They Actually Have Real Ability?

17. Example: Coin Flip
Nostradamus
Ho: Cannot Actually Predict Coin Flips
H1: Can Actually Predict Coin Flip
(i.e. do so at a rate greater than chance)
Ho is the Null Hypothesis
H1 is the Alternative Hypothesis

18. Reject the Null versus
Failing to Reject the Null
If We Fail to Reject the Null, we are left with the assumption
of no relationship
In the Coin Flip Example, We might have enough evidence
to reject the null
Remember the default (null) is that there is no
relationship
Although a Relationship might actually exist

19. Example: Coin Flip
Nostradamus
If He Were Guessing - what is the Probability Coin Flip
Nostradamus Predicts at least 3 of 4 Coin Tosses ?
p
probability of success
x
number of successes
n
number of trials
3 or 4 4 1/2

21. Example: Coin Flip
Nostradamus
If He Were Guessing - what is the Probability Coin Flip
Nostradamus Predicts at least 3 of 4 Coin Tosses ?
p
probability of success
x
number of successes
n
number of trials
3 or 4 4 1/2

22. Example: Coin Flip
Nostradamus
If He Were Guessing - what is the Probability Coin Flip
Nostradamus Predicts at least 3 of 4 Coin Tosses ?
#Here We Get Only For X=3

23. Example: Coin Flip
Nostradamus
If He Were Guessing - what is the Probability Coin Flip
Nostradamus Predicts at least 3 of 4 Coin Tosses ?
#Here We Get Only For X=3
#Now We Get a Vector if X=3, X=4

24. Example: Coin Flip
Nostradamus
If He Were Guessing - what is the Probability Coin Flip
Nostradamus Predicts at least 3 of 4 Coin Tosses ?
#Here We Get Only For X=3
#Now We Get The
Sum of X=3, X=4
#Now We Get a Vector if X=3, X=4

25. Does 30 heads in 50 flips imply an unfair coin?

26. Does 30 heads in 50 flips imply an unfair coin?

27. Does 30 heads in 50 flips imply an unfair coin?
Assuming a Fair Coin - what is the 95% Conf. Interval for 50 flips?

28. Does 30 heads in 50 flips imply an unfair coin?
Assuming a Fair Coin - what is the 95% Conf. Interval for 50 flips?

29. Imagine that I gave out a 15
question multiple choice test
with 5 possible answers per
question.

30. Imagine that I gave out a 15
question multiple choice test
with 5 possible answers per
question.
Using random guessing, what is the probability of
getting exactly 7 questions correct?

31. Imagine that I gave out a 15
question multiple choice test
with 5 possible answers per
question.
p
probability of success
x
number of successes
n
number of trials
7 15 1/5
Using random guessing, what is the probability of
getting exactly 7 questions correct?

32. Imagine that I gave out a 15
question multiple choice test
with 5 possible answers per
question.
p
probability of success
x
number of successes
n
number of trials
7 15 1/5
Using random guessing, what is the probability of
getting exactly 7 questions correct?

33. Imagine that I gave out a 15
question multiple choice test
with 5 possible answers per
question.
p
probability of success
x
number of successes
n
number of trials
7 15 1/5
Using random guessing, what is the probability of
getting exactly 7 questions correct?
This is the exact probability for 7
But What About 7 or Greater?

34. Imagine that I gave out a 15
question multiple choice test
with 5 possible answers per
question.
Using random guessing, what is the probability of
getting greater than 7 questions correct?
This is our prior answer
Here we are summing 7:15

35. Normal Distribution

36. Imagine that a population of students
take a test with an average score of 78
and a standard deviation of 9.
Assuming the test scores are normally
distributed, how many students
received a 90 or higher?

38. Imagine that a population 100
Students take a test with an
average score of 78
and a standard deviation of 9.
Assuming the test scores are
normally distributed, how many
students received a 90 or higher?

39. Imagine that a population 100
Students take a test with an
average score of 78
and a standard deviation of 9.
Assuming the test scores are
normally distributed, how many
students received a 90 or higher?
pnorm(q , mean= , sd= , lower.tail=TRUE) This is the Syntax:

40. Imagine that a population 100
Students take a test with an
average score of 78
and a standard deviation of 9.
Assuming the test scores are
normally distributed, how many
students received a 90 or higher?
pnorm(q , mean= , sd= , lower.tail=TRUE) This is the Syntax:
pnorm(90 , mean= 78 , sd=9 , lower.tail=FALSE) What We Want:
because we want upper tail

41. Imagine that a population 100
Students take a test with an
average score of 78
and a standard deviation of 9.
Assuming the test scores are
normally distributed, how many
students received a 90 or higher?
pnorm(q , mean= , sd= , lower.tail=TRUE) This is the Syntax:
pnorm(90 , mean= 78 , sd=9 , lower.tail=FALSE) What We Want:
because we want upper tail

42. In the 2011-2012 year the national
average on the LSAT was 150.66
with a Standard Deviation of
10.19
Assuming those scores are
normally distributed, what
percentage of test takers scored
160 or above? http://www.lsac.org/docs/default-source/
research-%28lsac-resources%29/tr-12-03.pdf
Table 1 on Page 9

43. In the 2011-2012 year the national
average on the LSAT was 150.66
with a Standard Deviation of
10.19
Assuming those scores are
normally distributed, what
percentage of test takers scored
160 or above? http://www.lsac.org/docs/default-source/
research-%28lsac-resources%29/tr-12-03.pdf
Table 1 on Page 9

44. Hypothesis Testing

45. 235,000
175,000
750,000
230,000
450,000
150,000
1,000,060
910,000
150,000
220,000
130,000
170,000
234,000
450,000
890,000
101,000
120,000
560,000
321,000
456,000
102,000
30,000
793,000
250,900
862,000
673,000
463,000
54,000
39,000
687,000
260,800
682,000
3,514,000
67,000
356,000
13,000
42,000
4,000
402,000
943,000
961,600
630,000
398,800
52,000
976,500
540,000
Awards in Rest of State Awards in Bloom County
N = 21
N = 25
Are Damage Awards in
Bloom County Excessive?
H0: There is No Difference Between the Mean Damage Award
in Bloom County and the Mean Damage Award in the Rest of
the State
This is
a
Two
Sample
Problem

46. H0: There is No Difference Between the Mean Damage
Award in Bloom County and the Mean Damage Award in
the Rest of the State
Num of Obs. Mean Std. Dev.
GROUP 1
Rest of State
21 $371,621 $289,823
GROUP 2
Bloom County
25 $547,784 $703,314

47. Given the sample size we might consider a T-Test

48. But We Need To Check For Normality

49. Okay this means we need to use a non-parametric test
Good News is that is Available in

50. This is tricky because we have do
not have even sized samples
Also the Sample is Pretty Small
As reported on Page
274 of Lawless, et. al.

51. Chi Squared Test

52. Male Female Totals
Not Research Asst 319 323 642
Research Assistant 60 34 94
Total 379 357 736
RA’s Hired at a School are mostly Men
60 out of 94 RA’s are Men (See Above)
Could this just be chance or is it too large to be
explained by chance?
Chi Square ( ) Statisticχ 2

53. Male Female Totals
Not
Research
Asst
319 323 642
Research
Assistant
60 34 94
Total 379 357 736

54. F Statistic
F Test

55. 2500
1500
1500
1300
2000
1500
1500
2000
2000
1500
1400
1500
2000
800
3000
1500
2000
2000
1700
2500
2299
1900
2050
2101
1160
2101
1300
3500
900
995
1299
1900
995
771
1250
900
749
1200
950
1200
995
1300
1600
1601
1000
1371
2400
1500
1325
1500
1799
2780
1800
1399
2225
1700
3800
2299
1800
1450
1500
1000
1500
1799
1600
1600
2000
2500
1200
2500
2000
1500
Northern
District
Western
District
Southern
District
Eastern
District
Attorneys Fees in
Chapter 7 BK’s in Texas
Districts
(From Lawless, et al)
https://s3.amazonaws.com/KatzCloud/AttyFeesTexasBKDist.csv

57. Daniel Martin Katz
@ computational
computationallegalstudies.com
lexpredict.com
danielmartinkatz.com
illinois tech - chicago kent college of law@