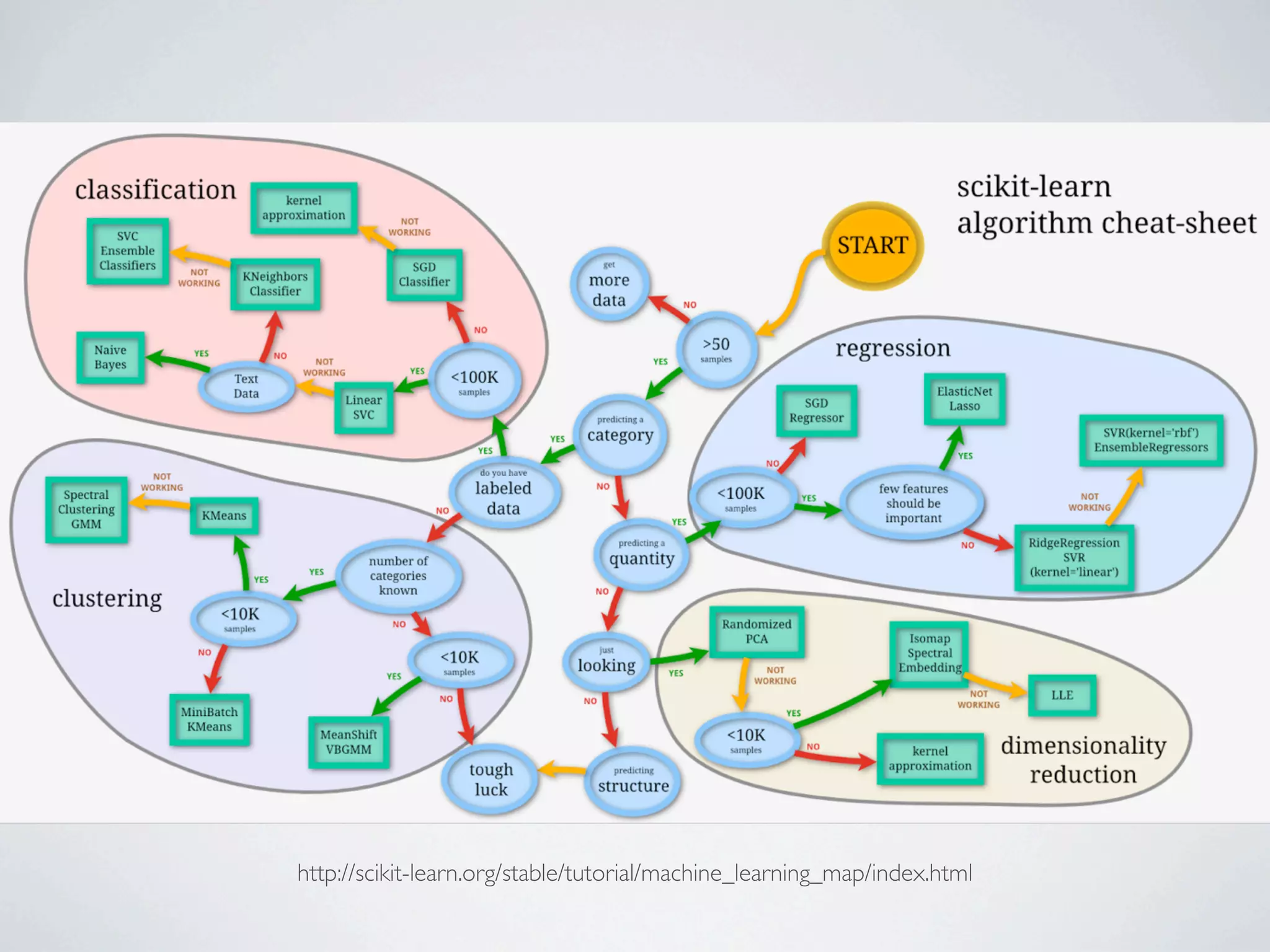
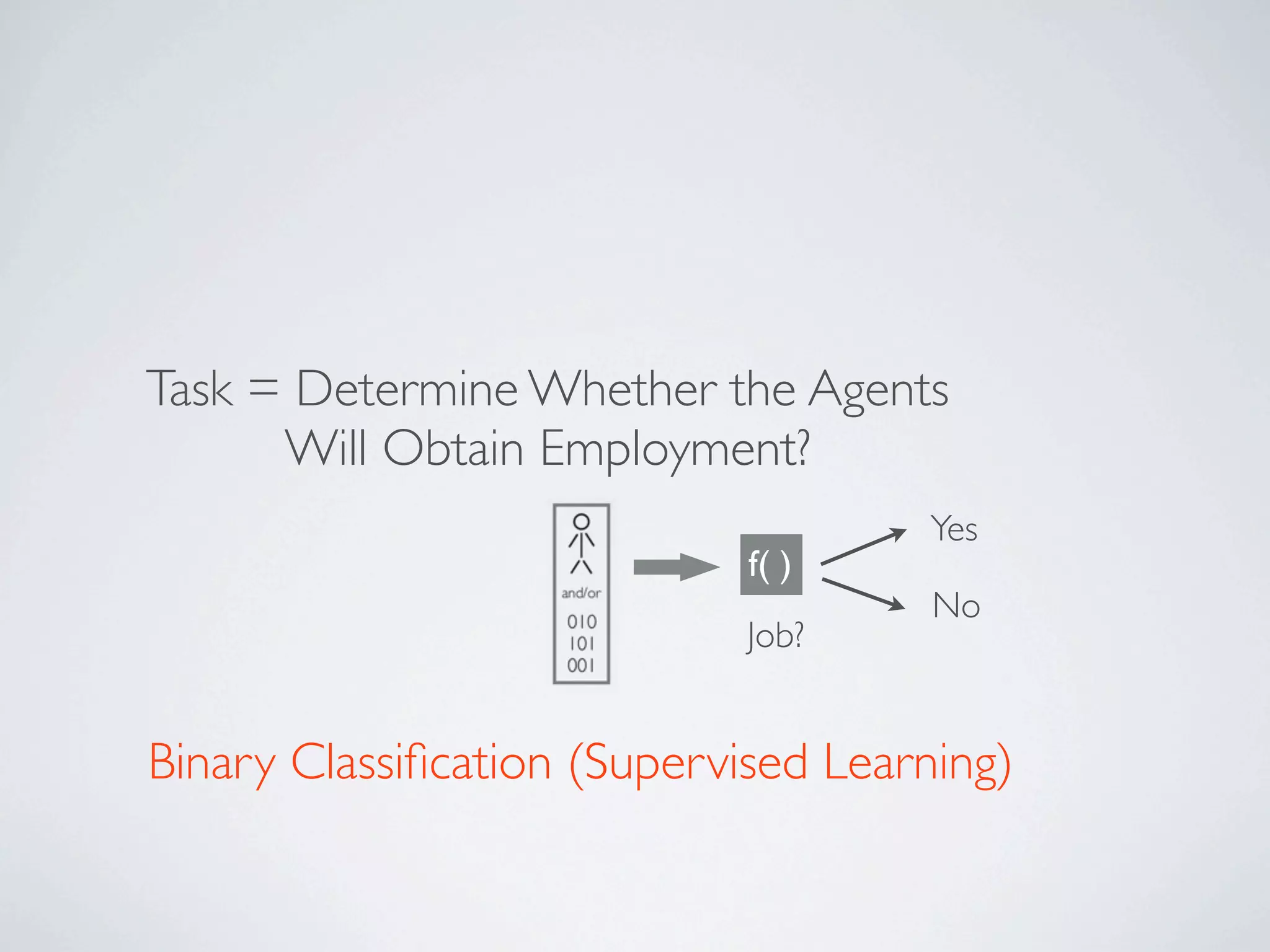
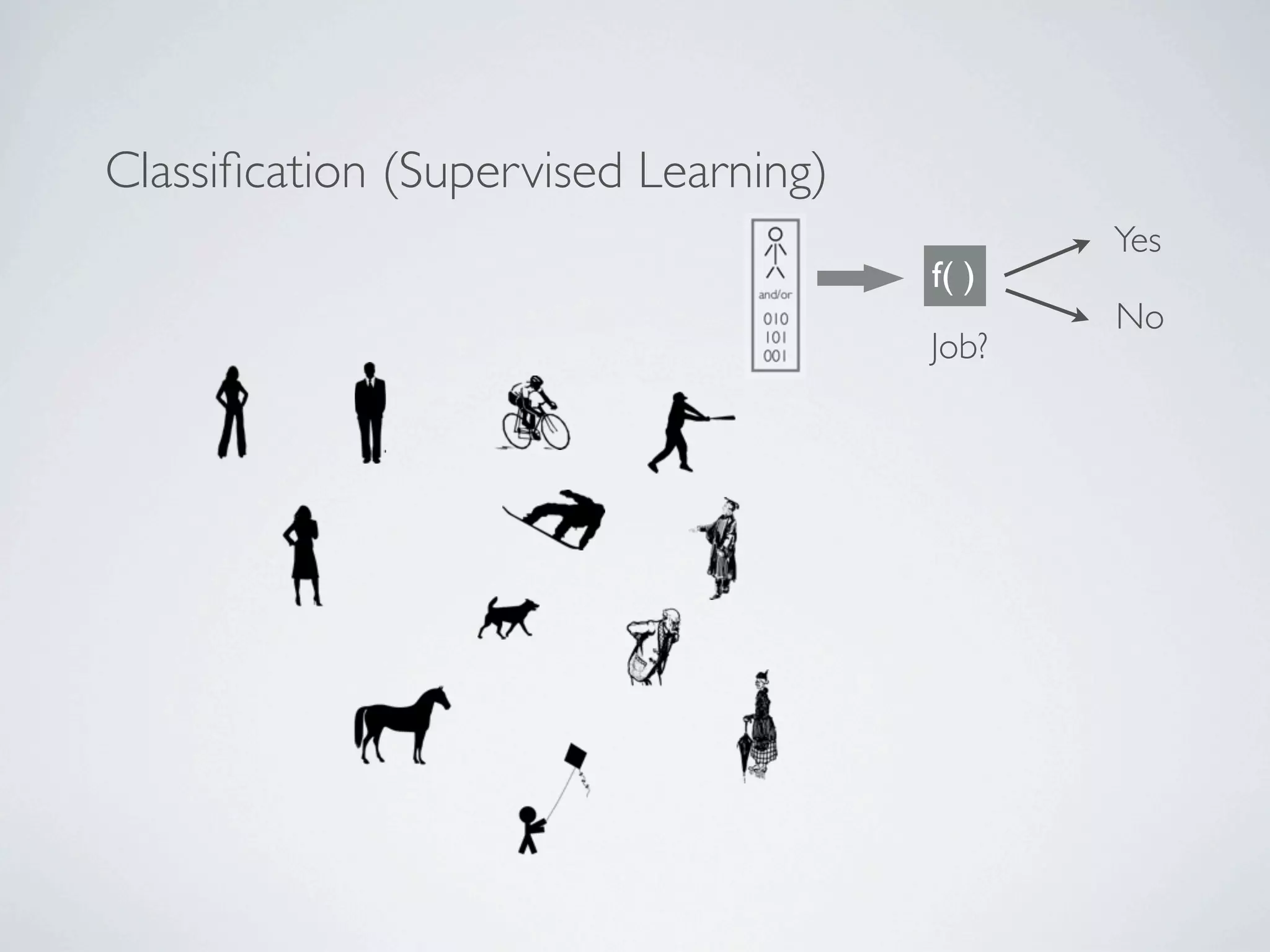
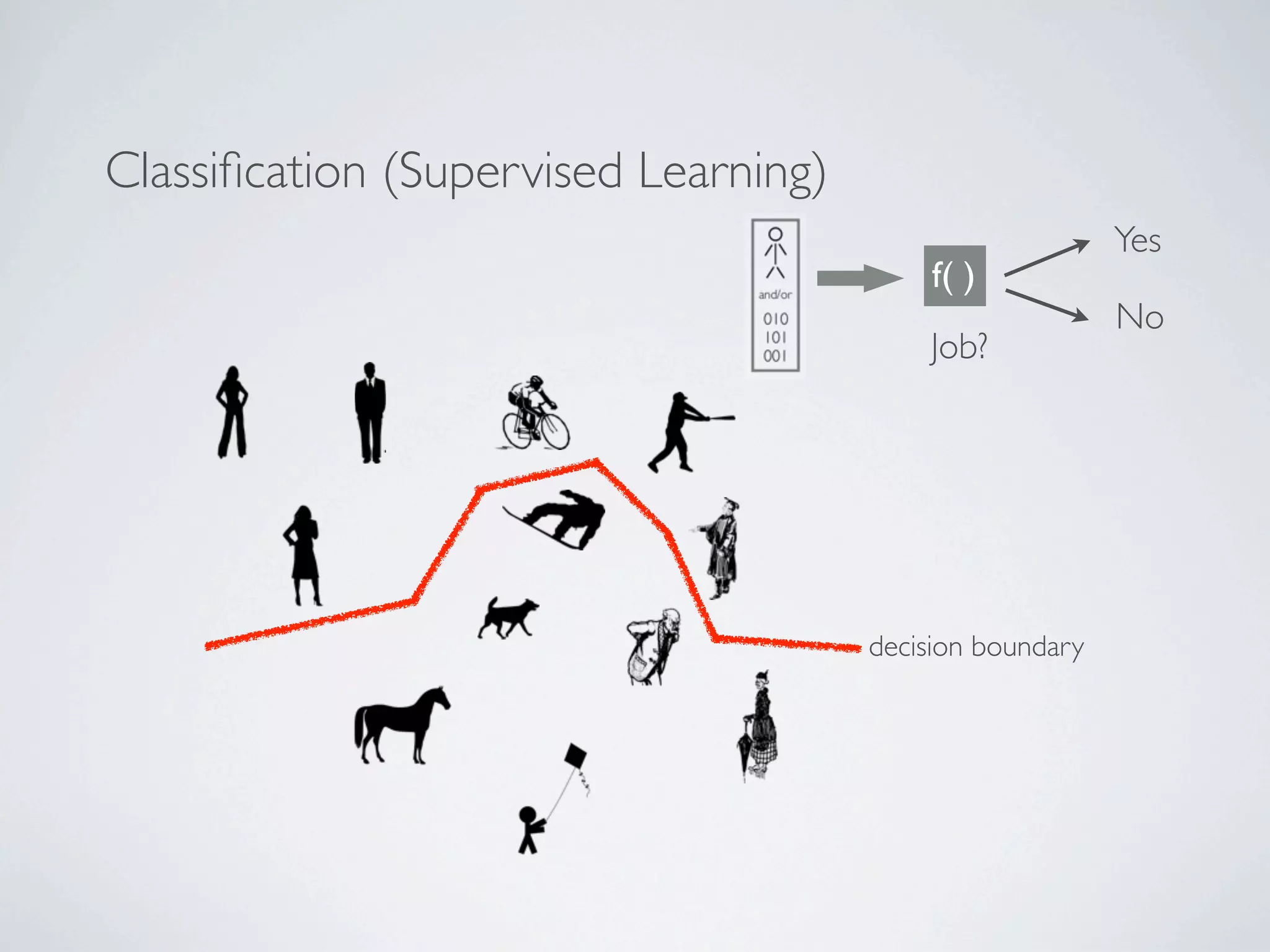
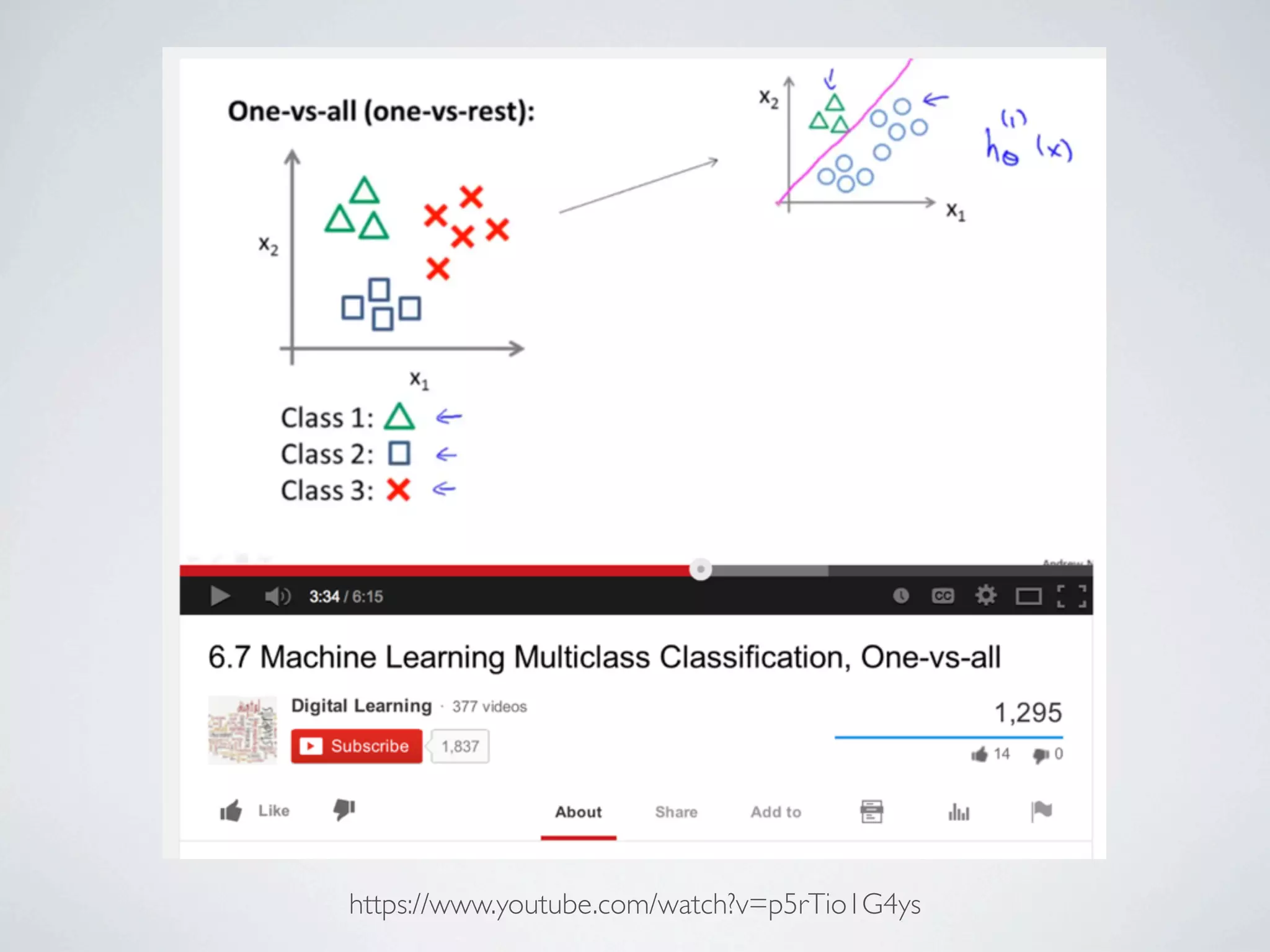
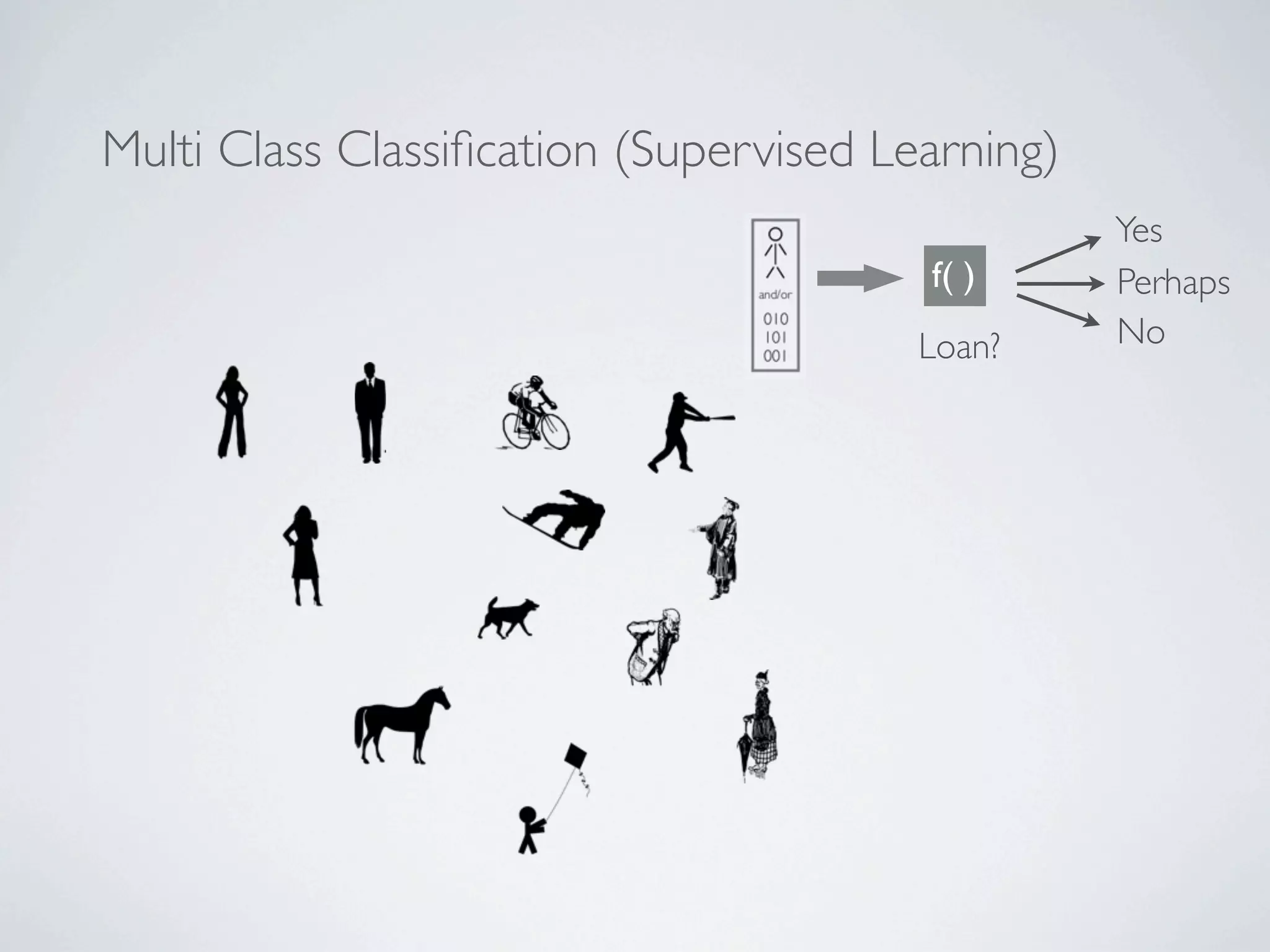
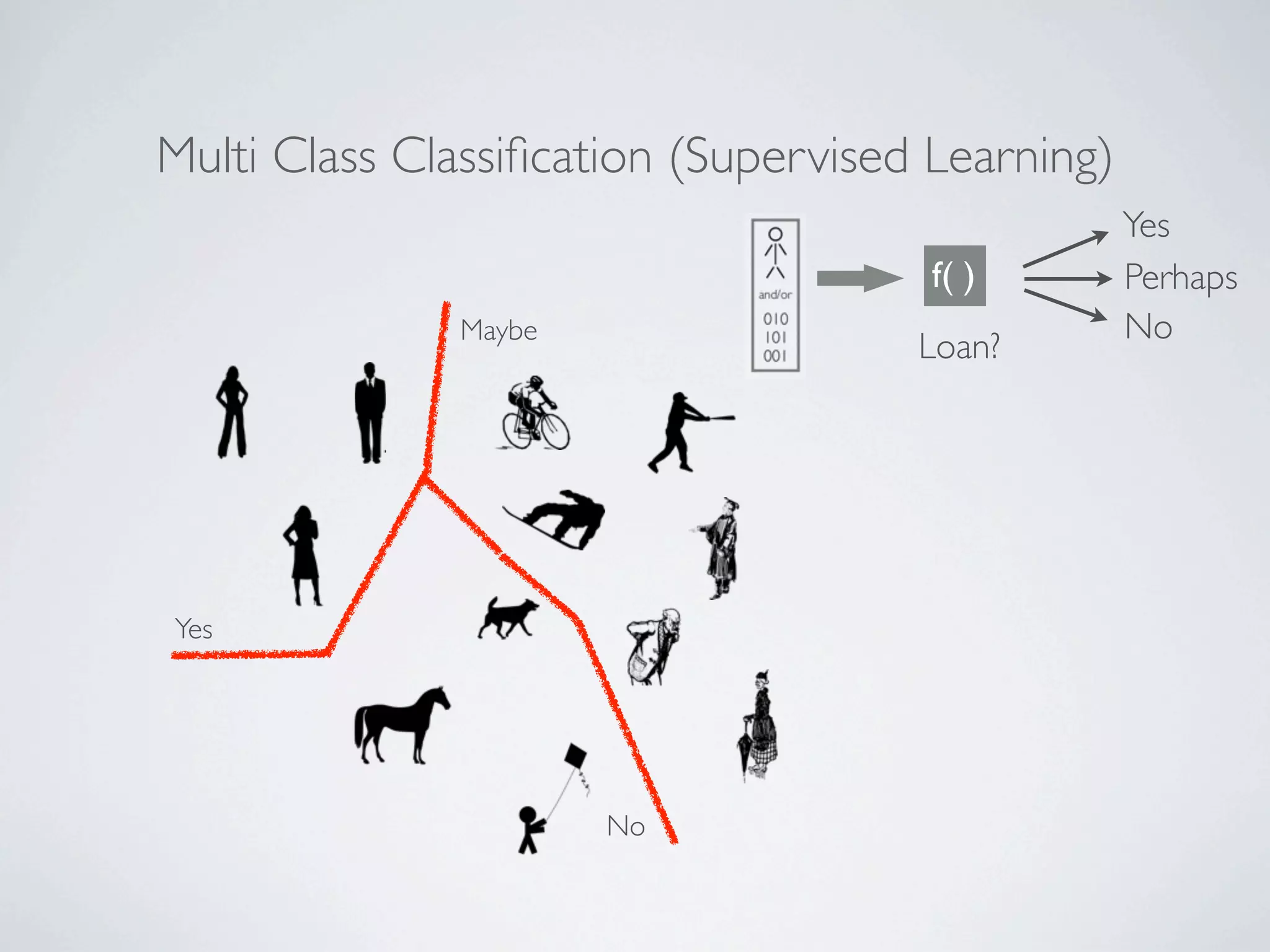
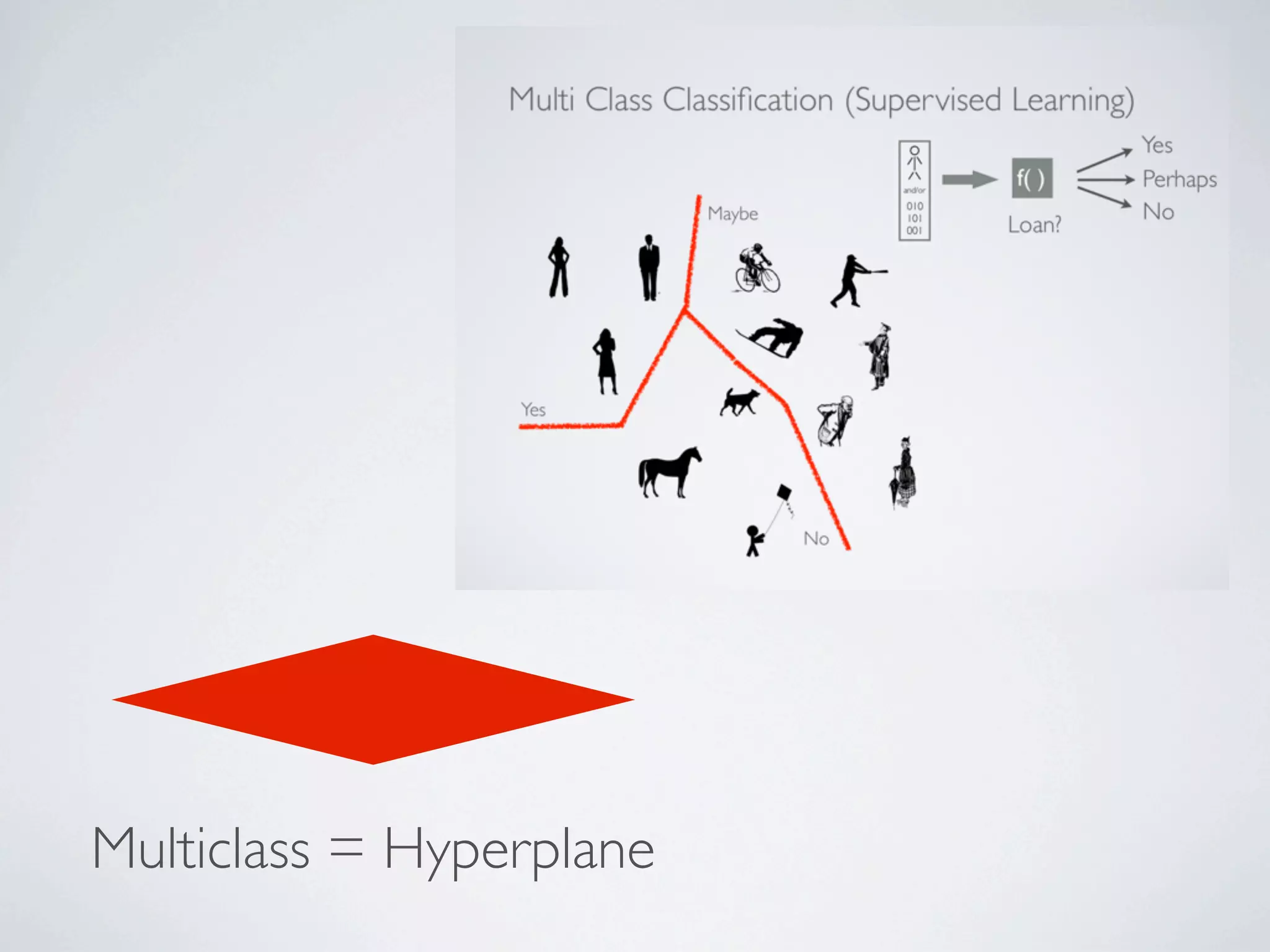
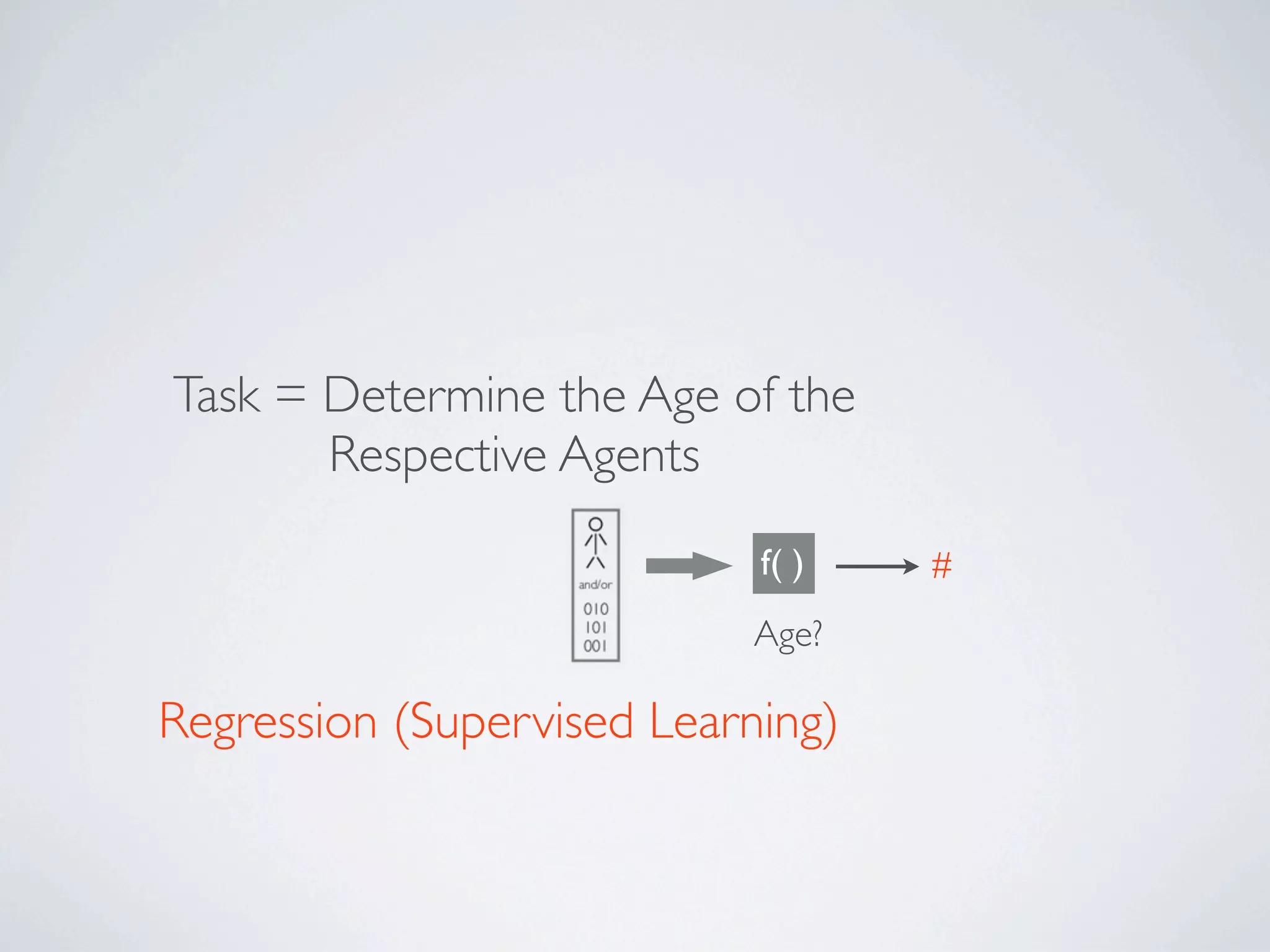
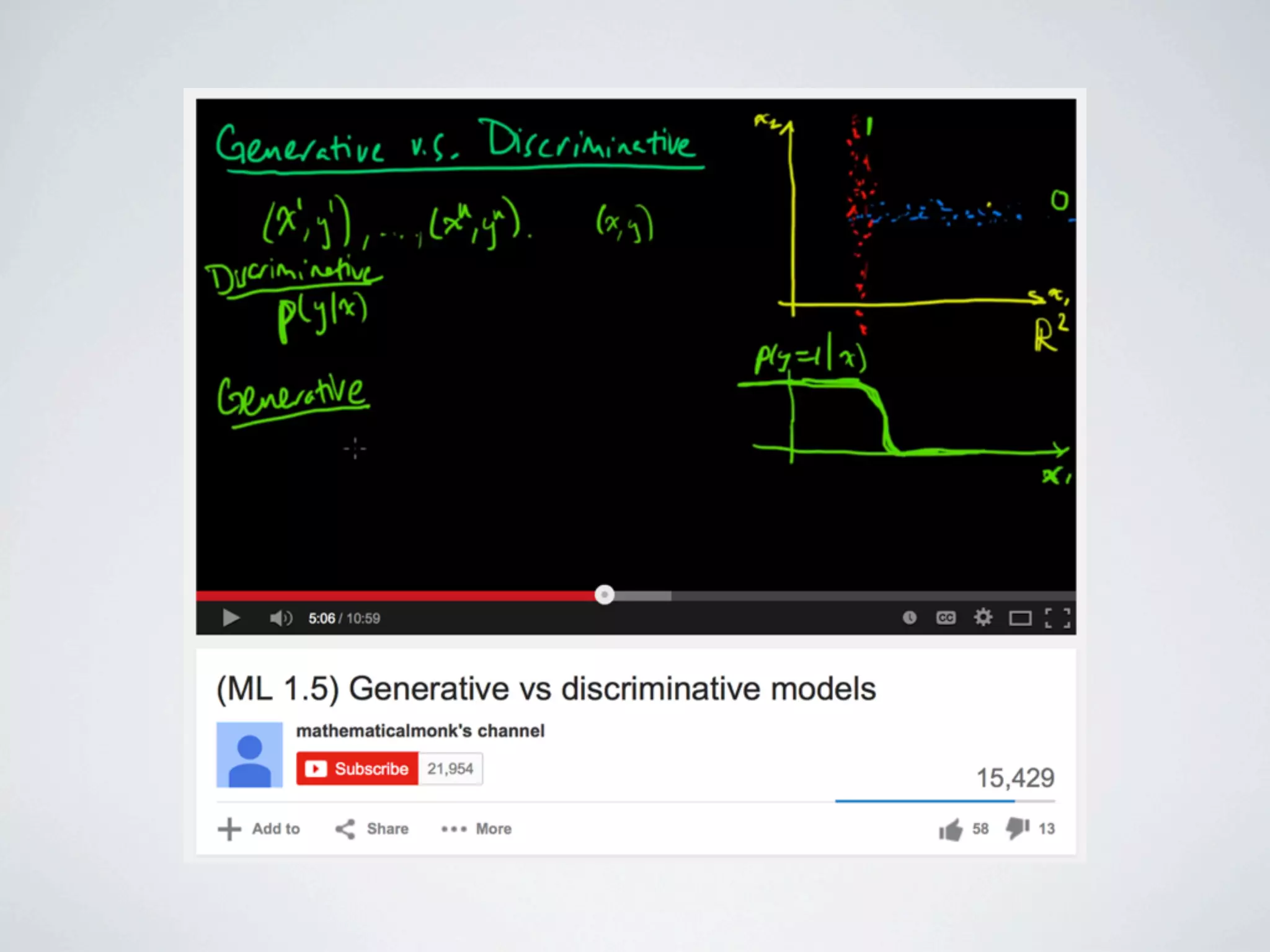
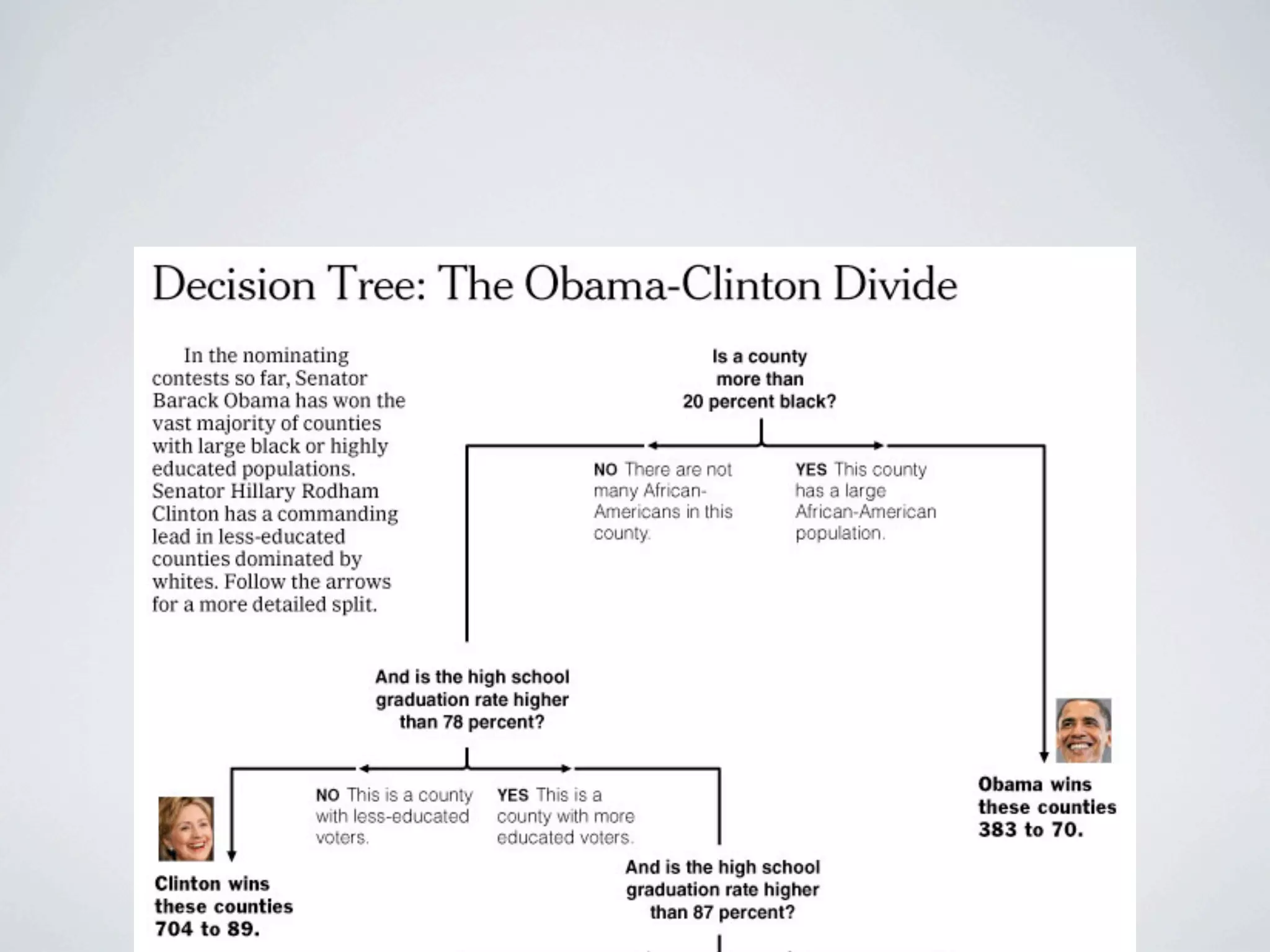
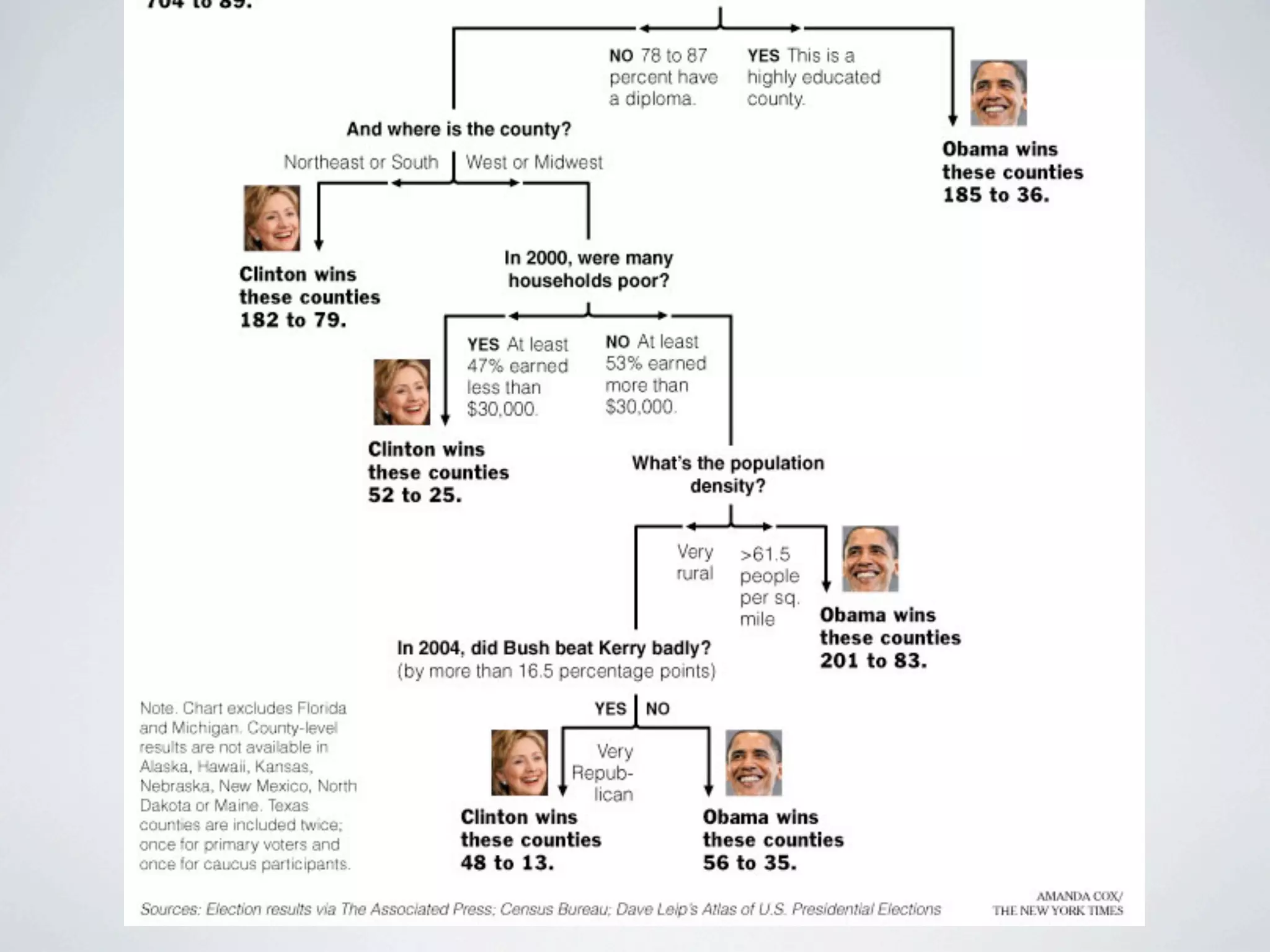
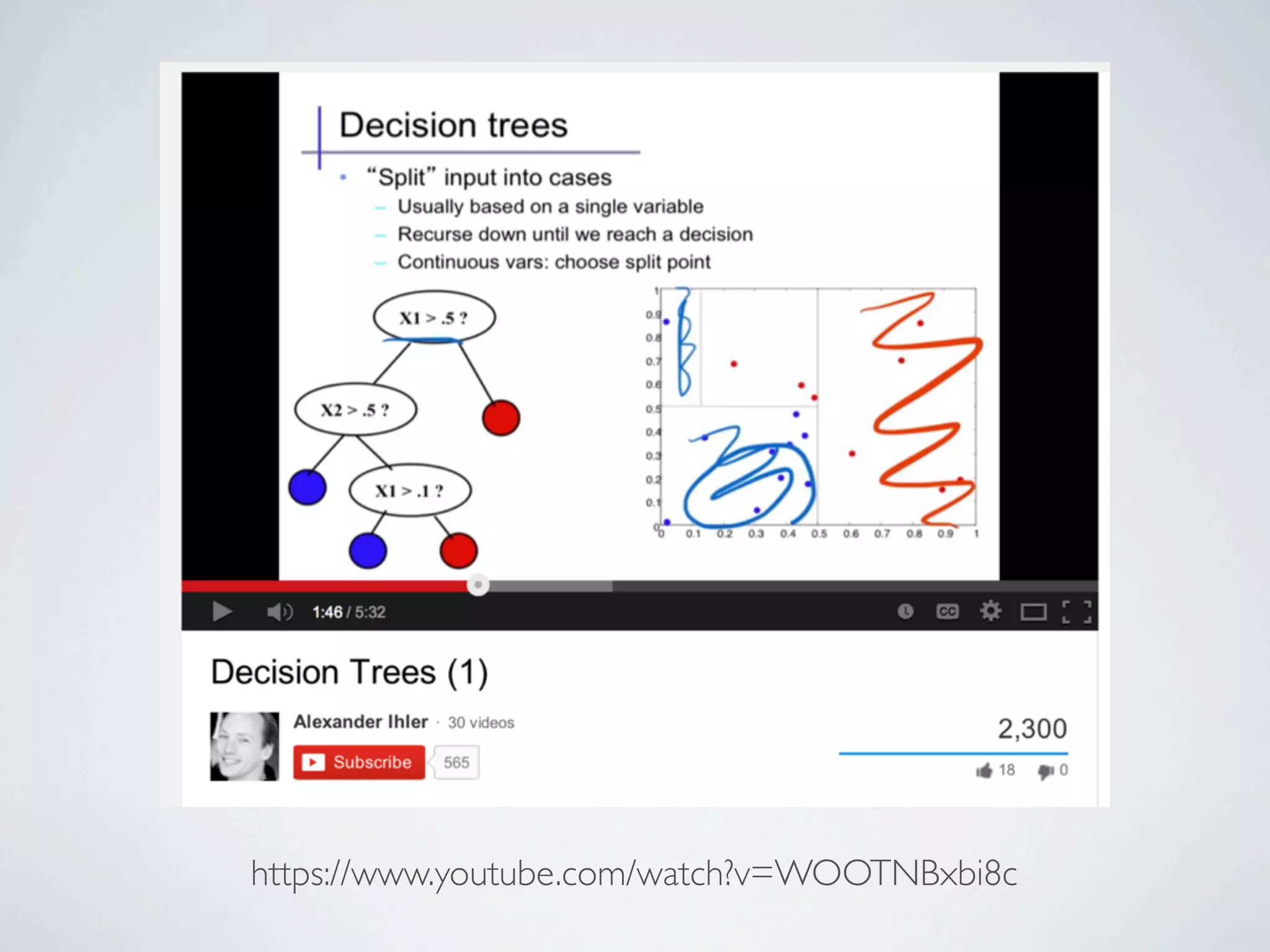
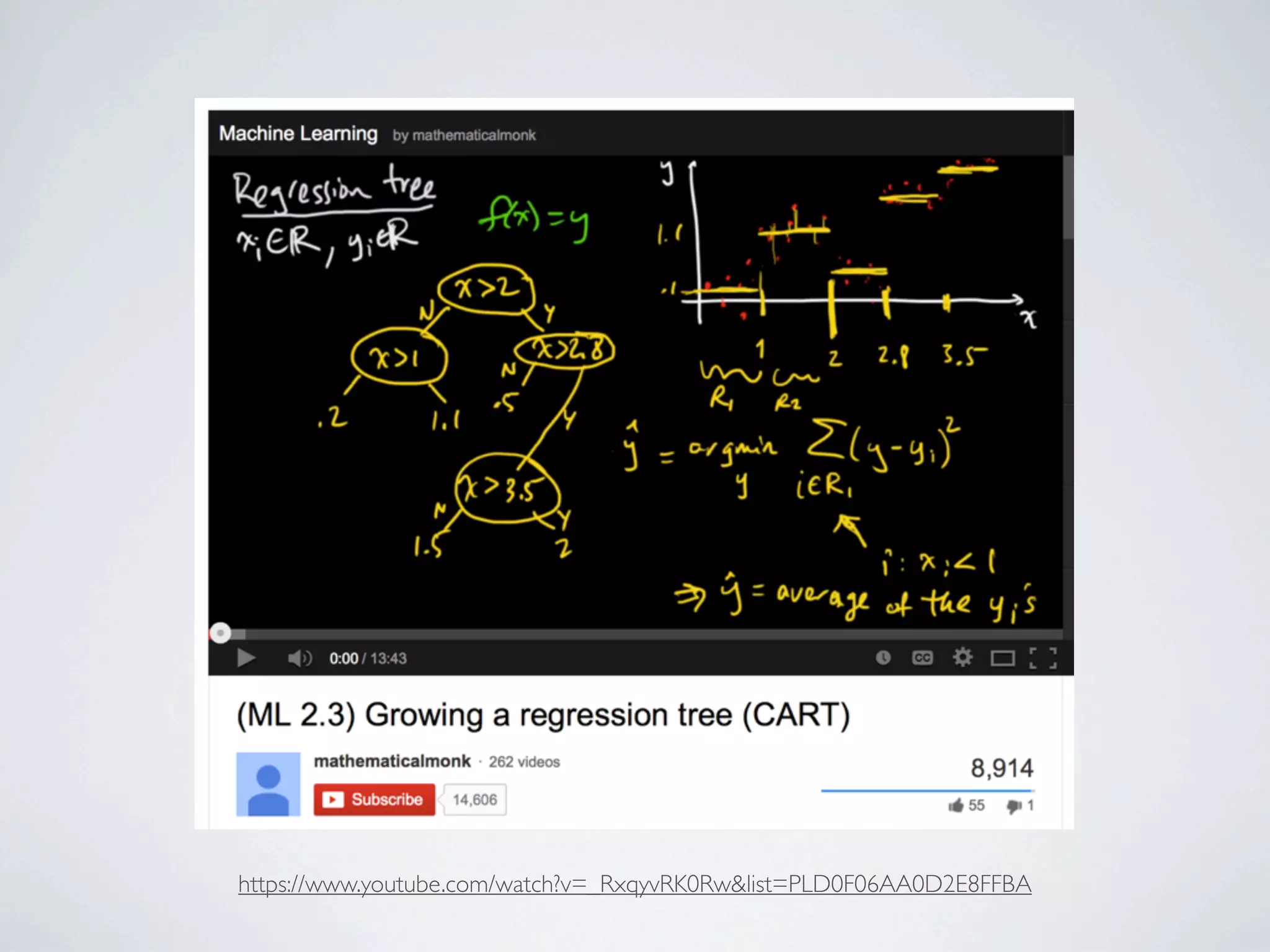
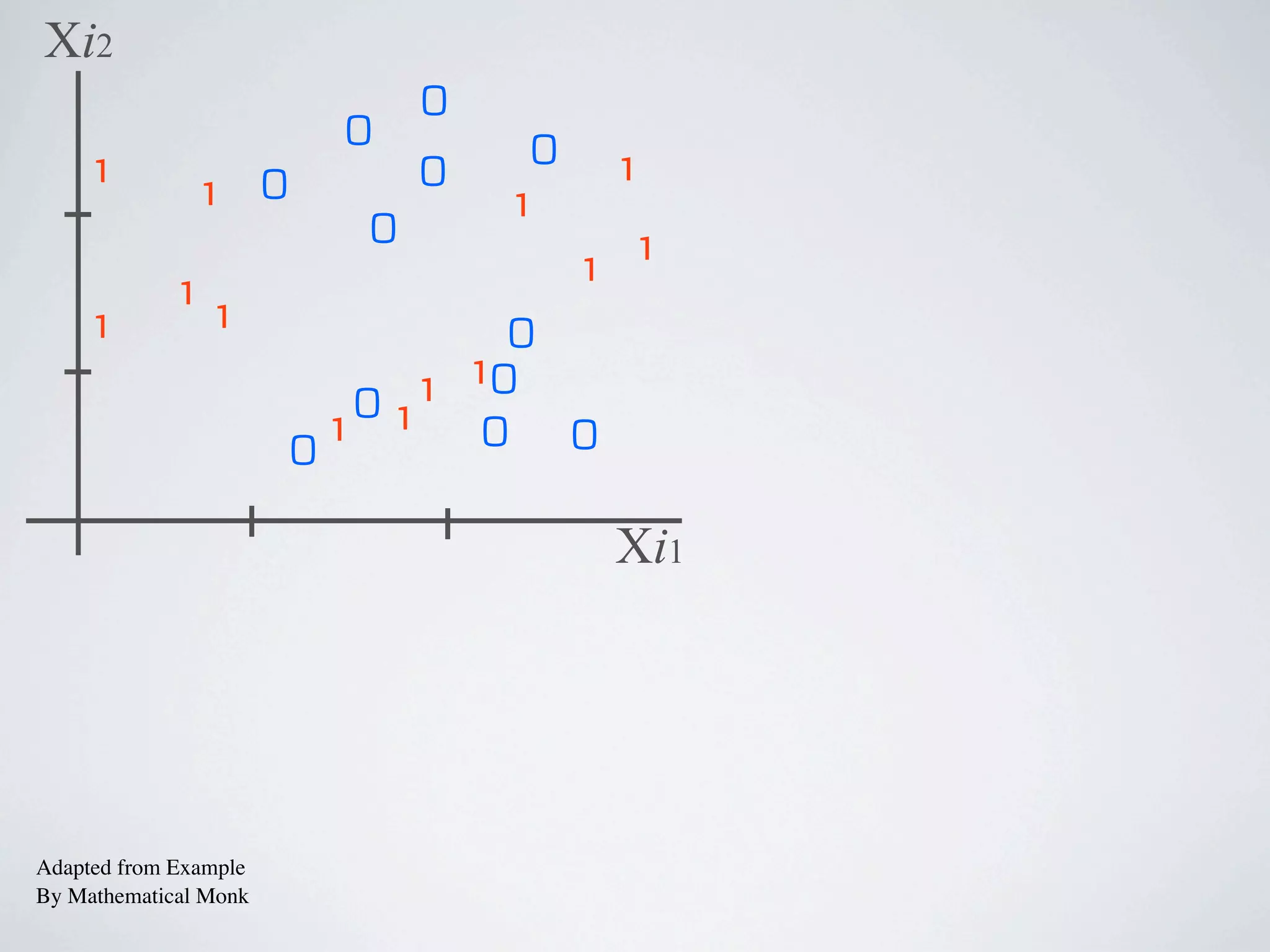
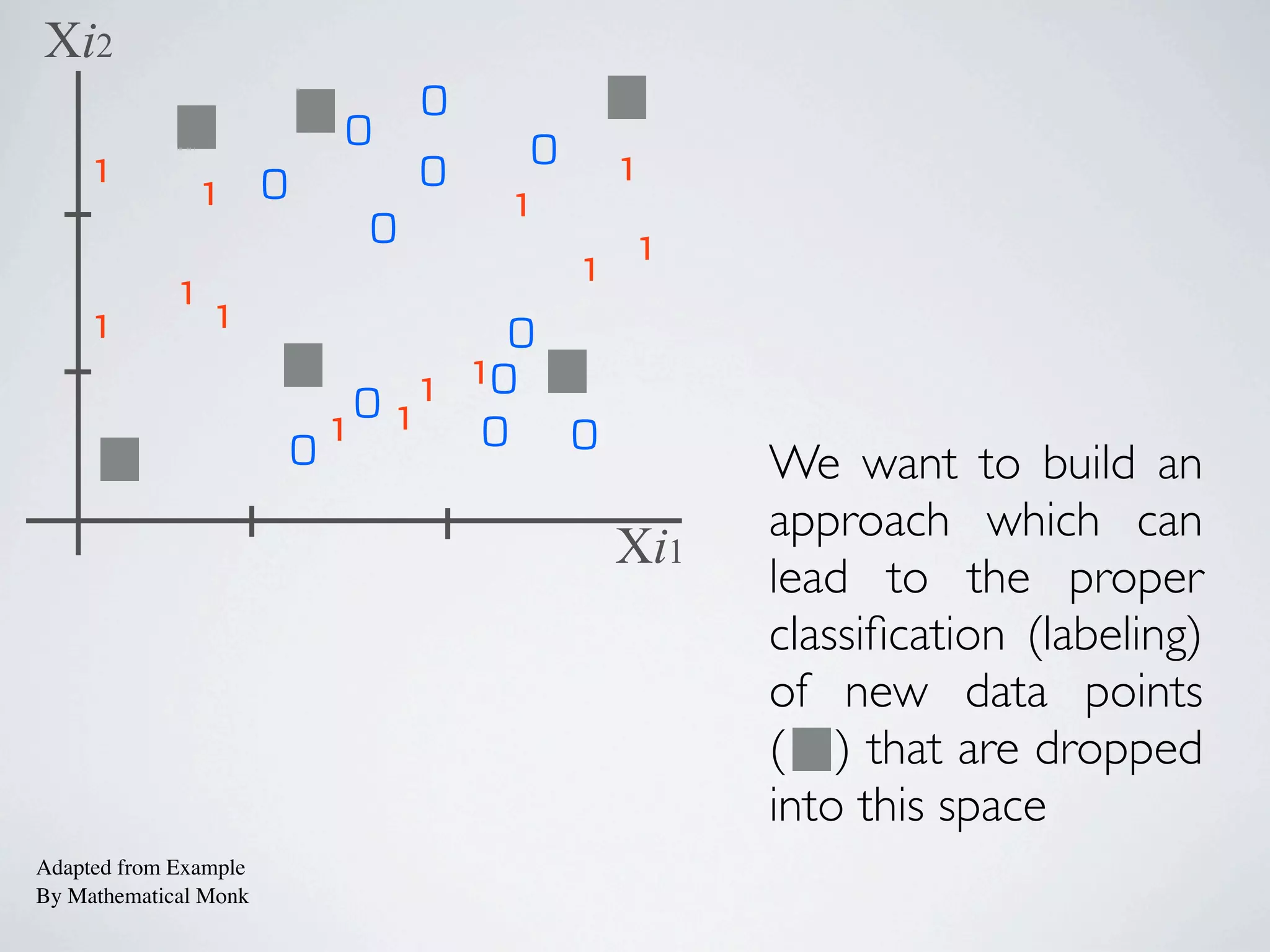
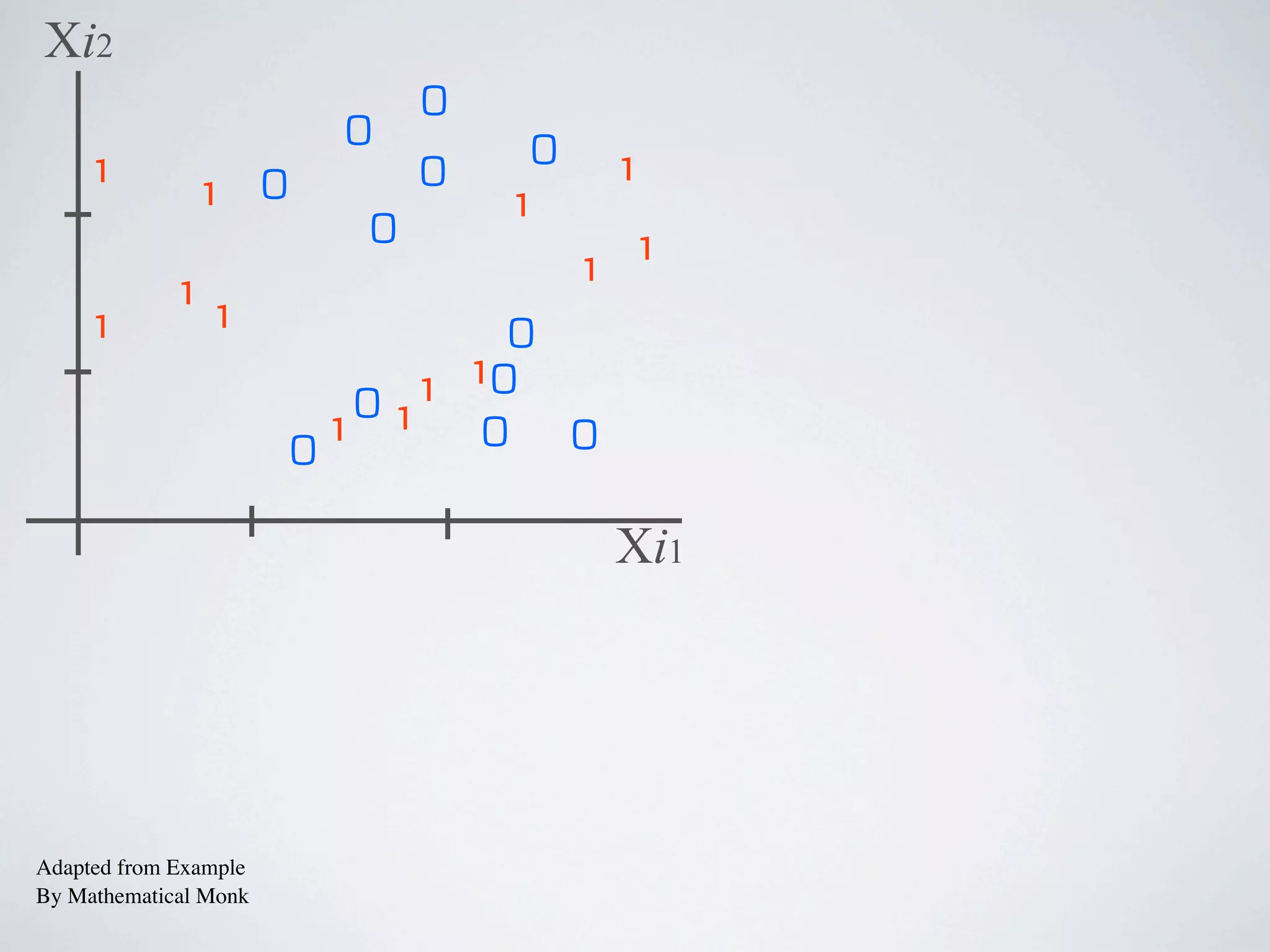
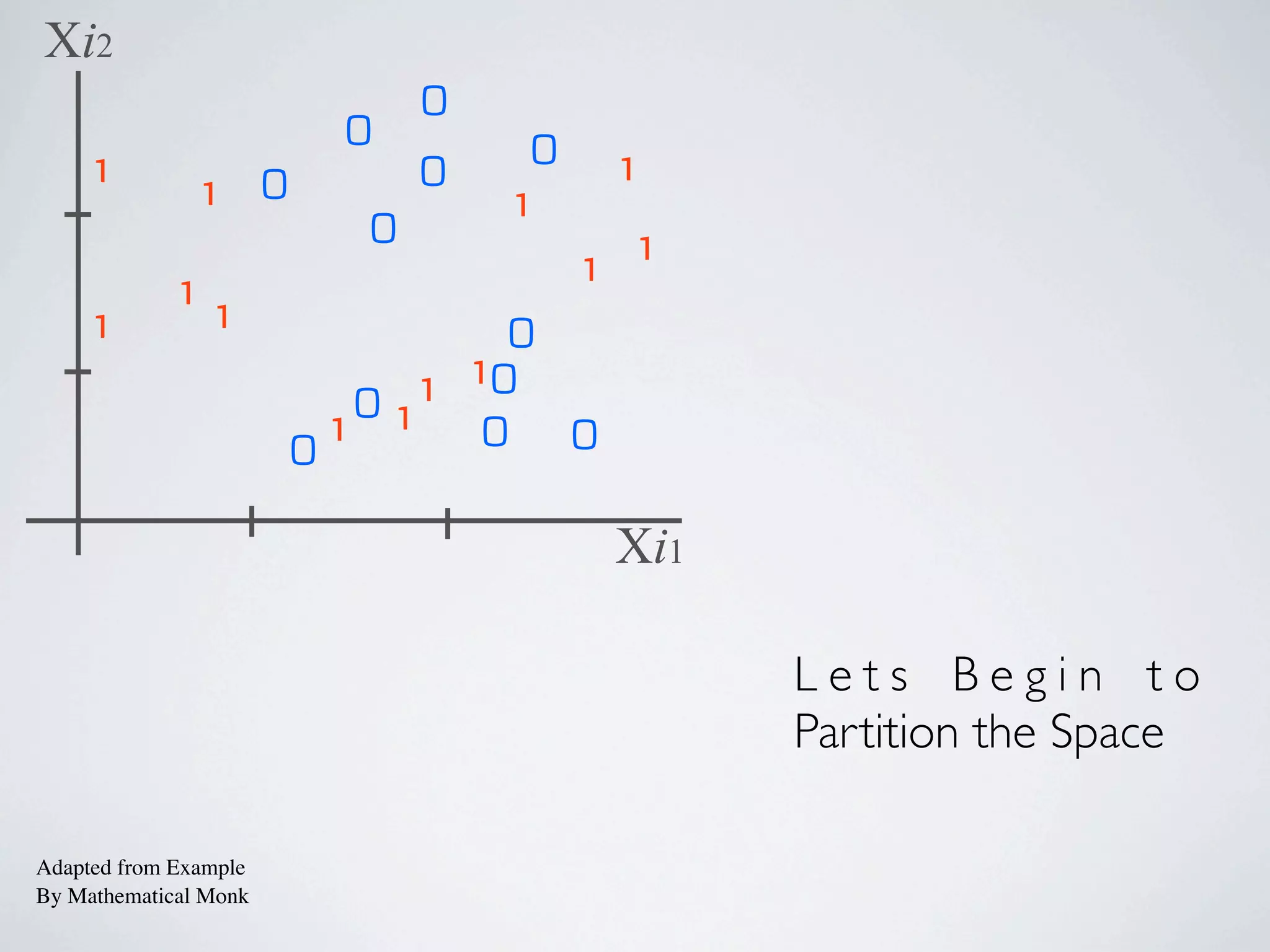
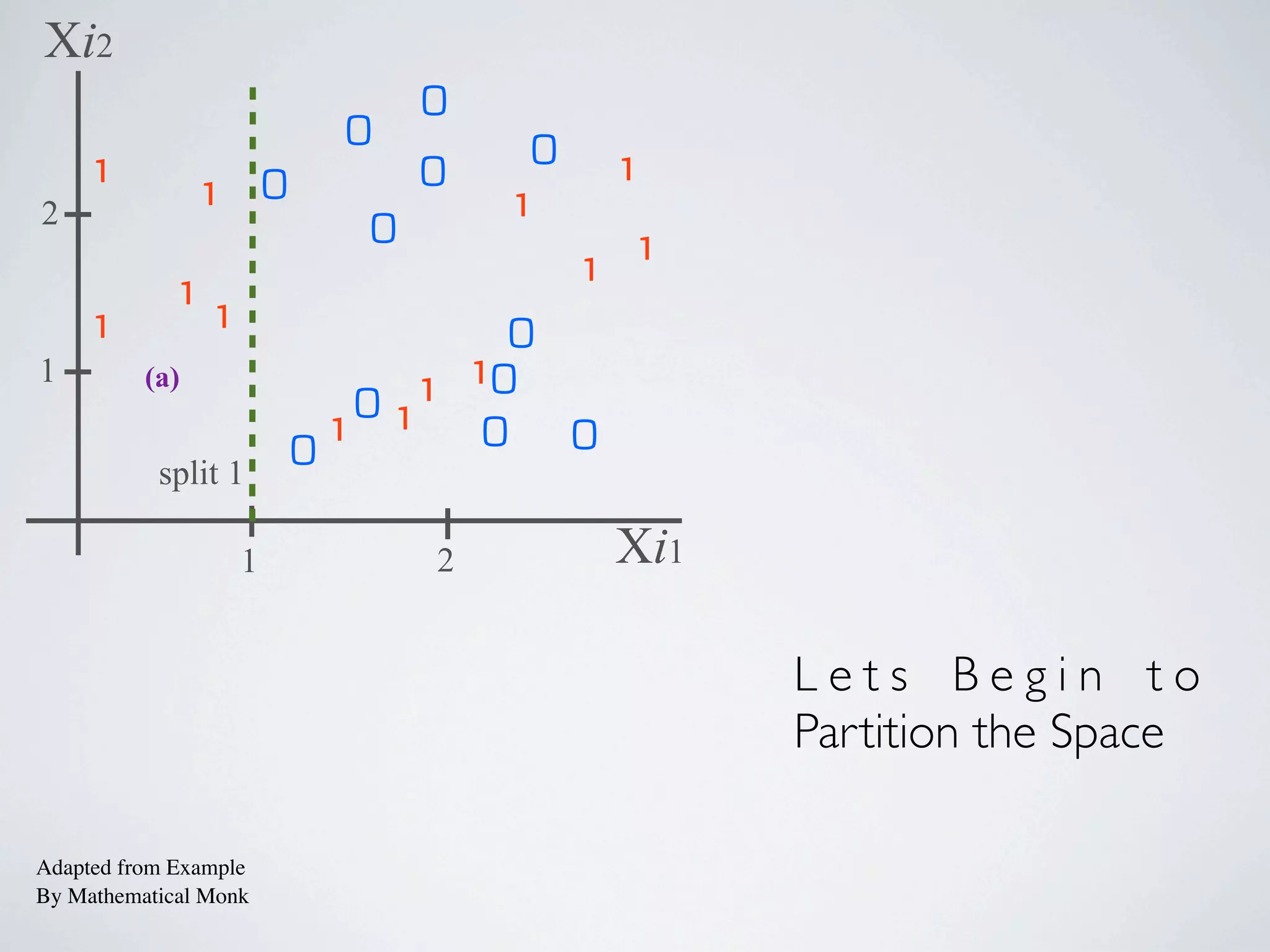
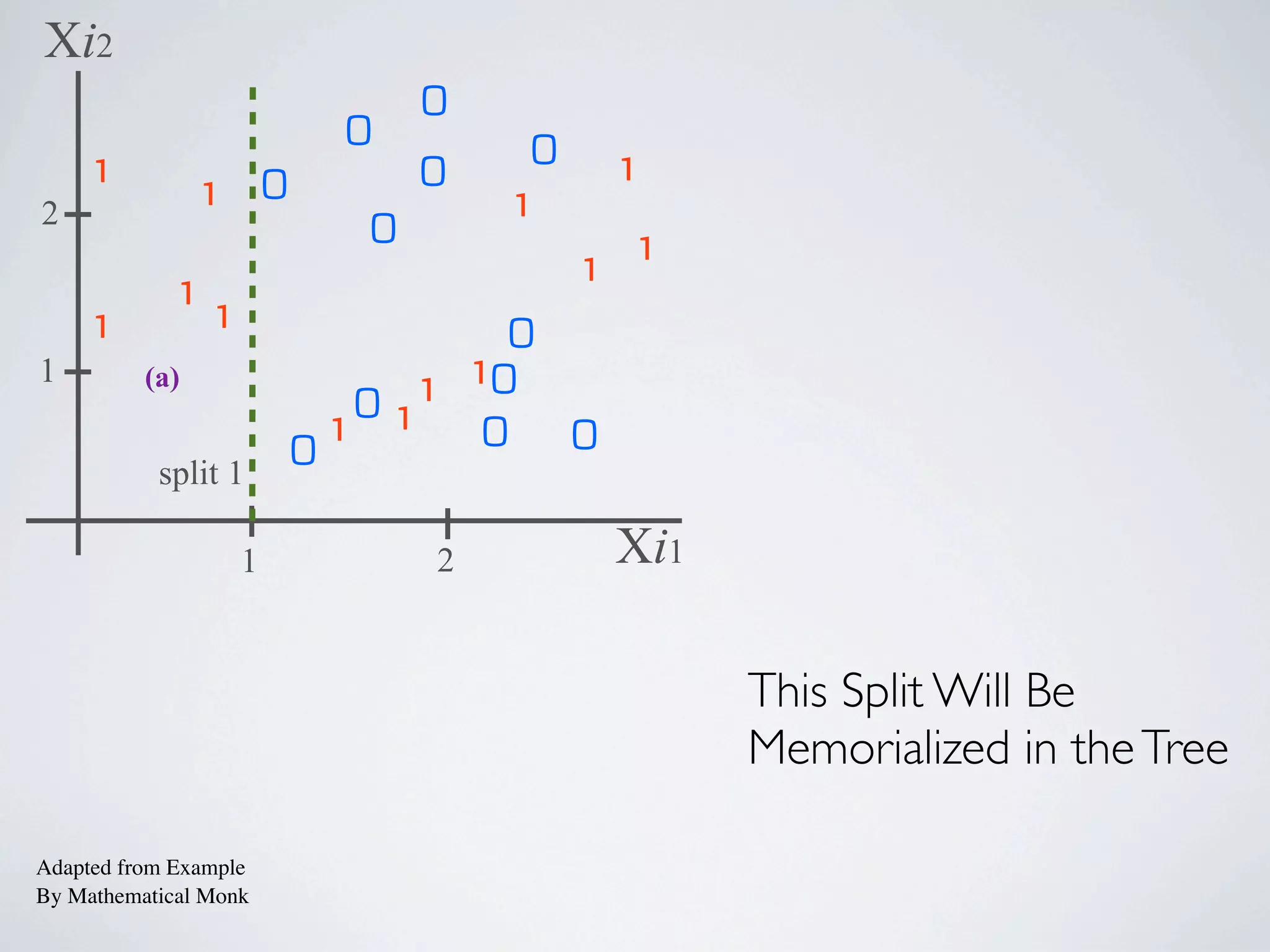
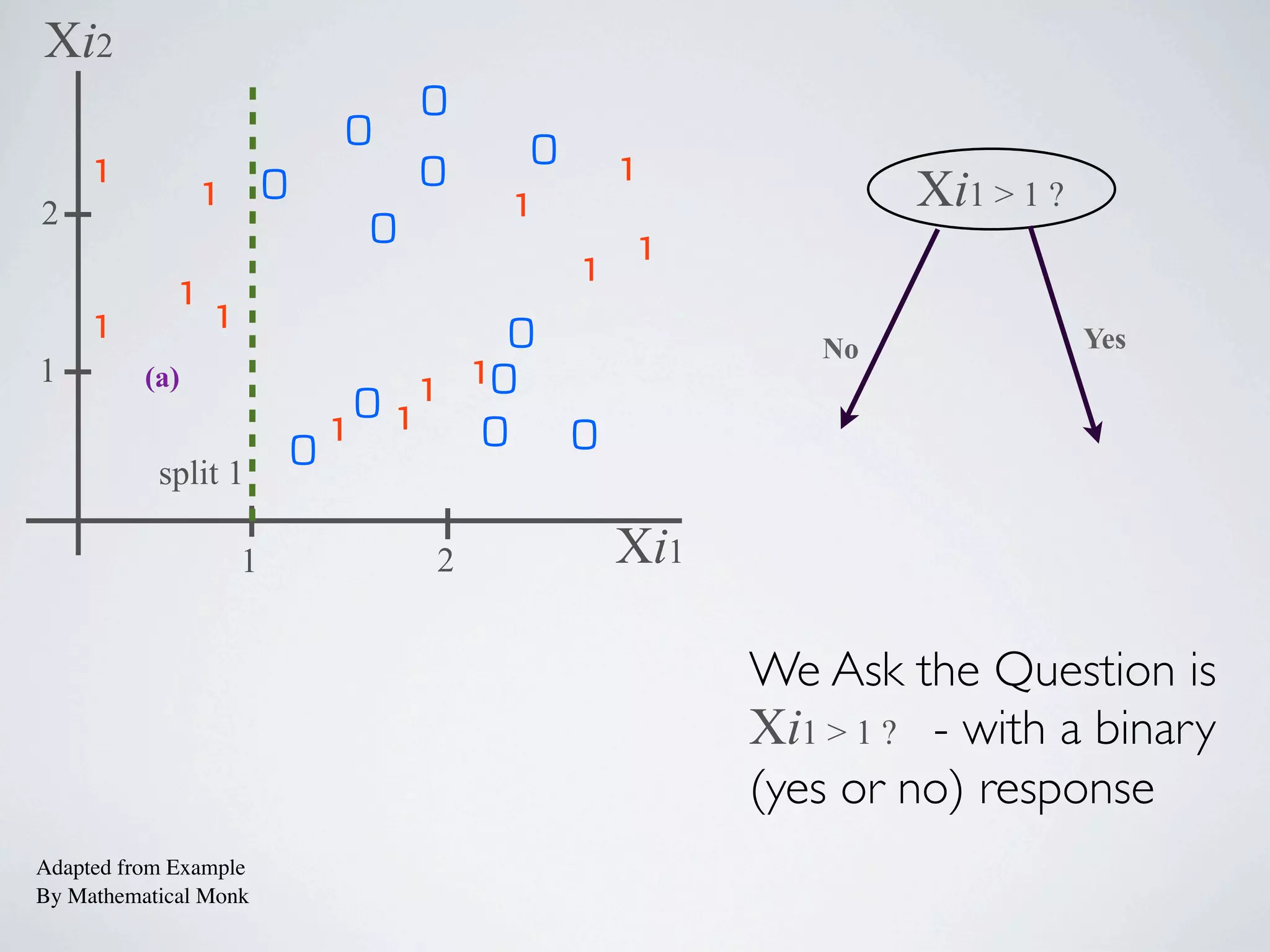
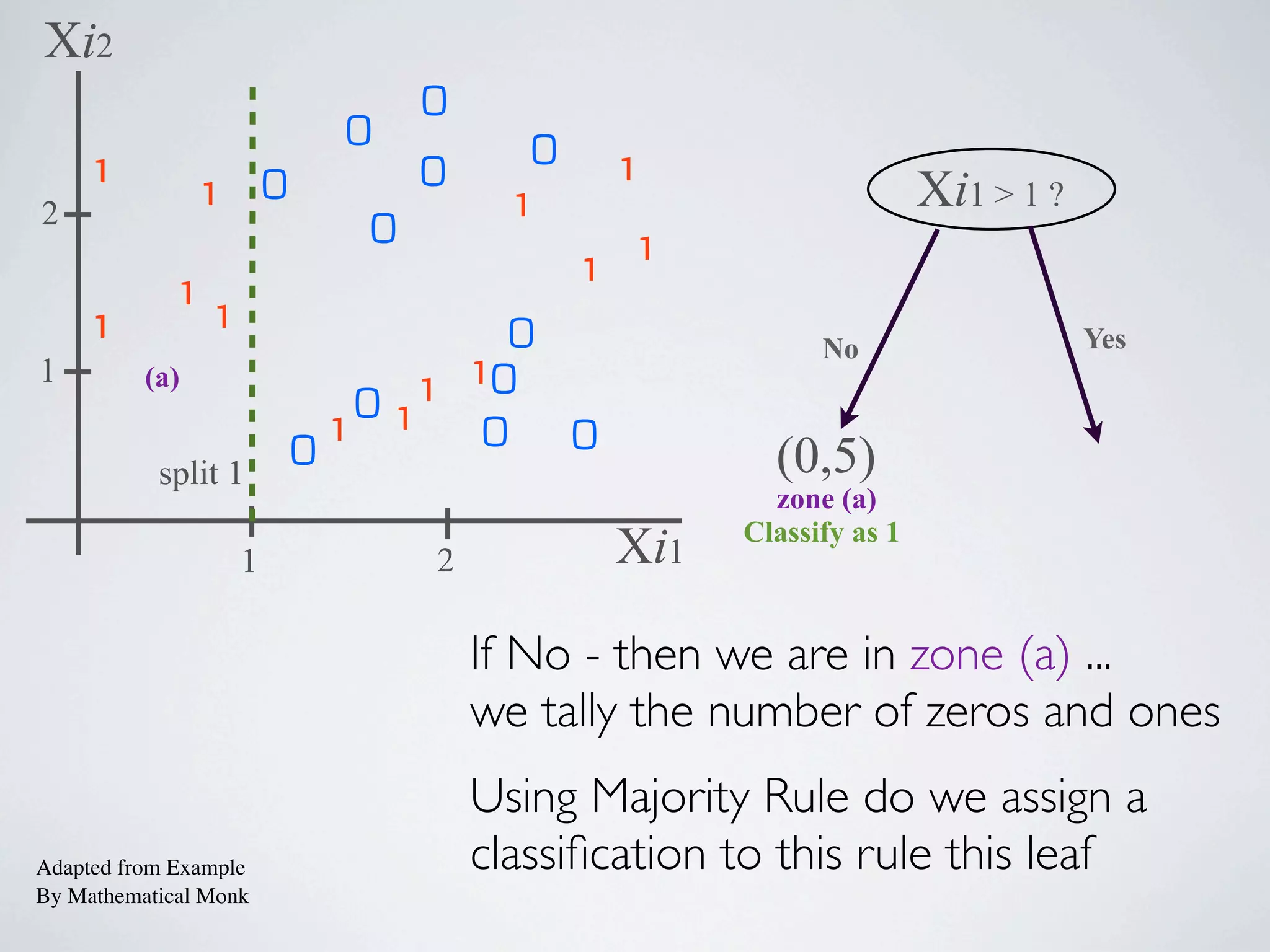
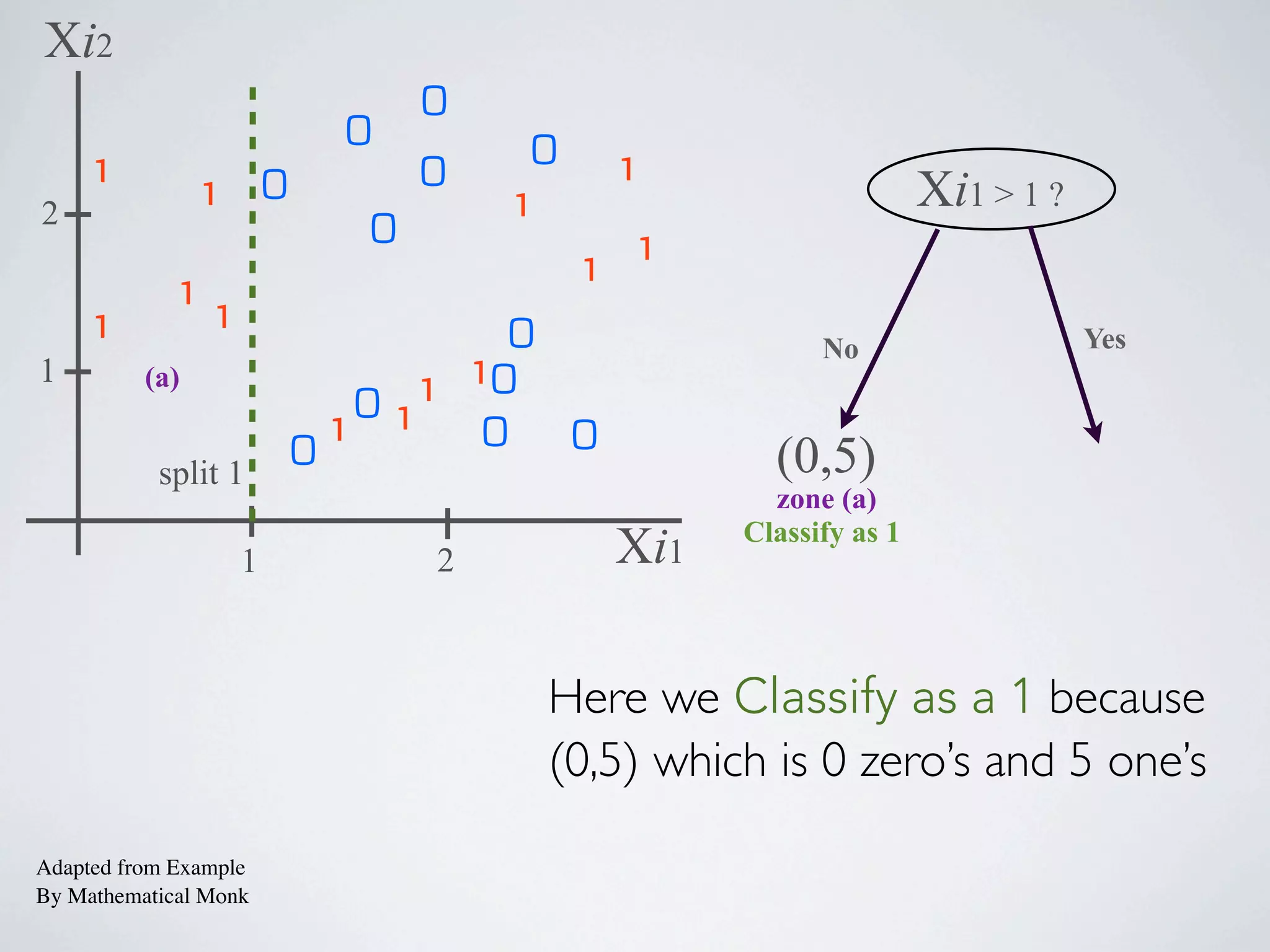
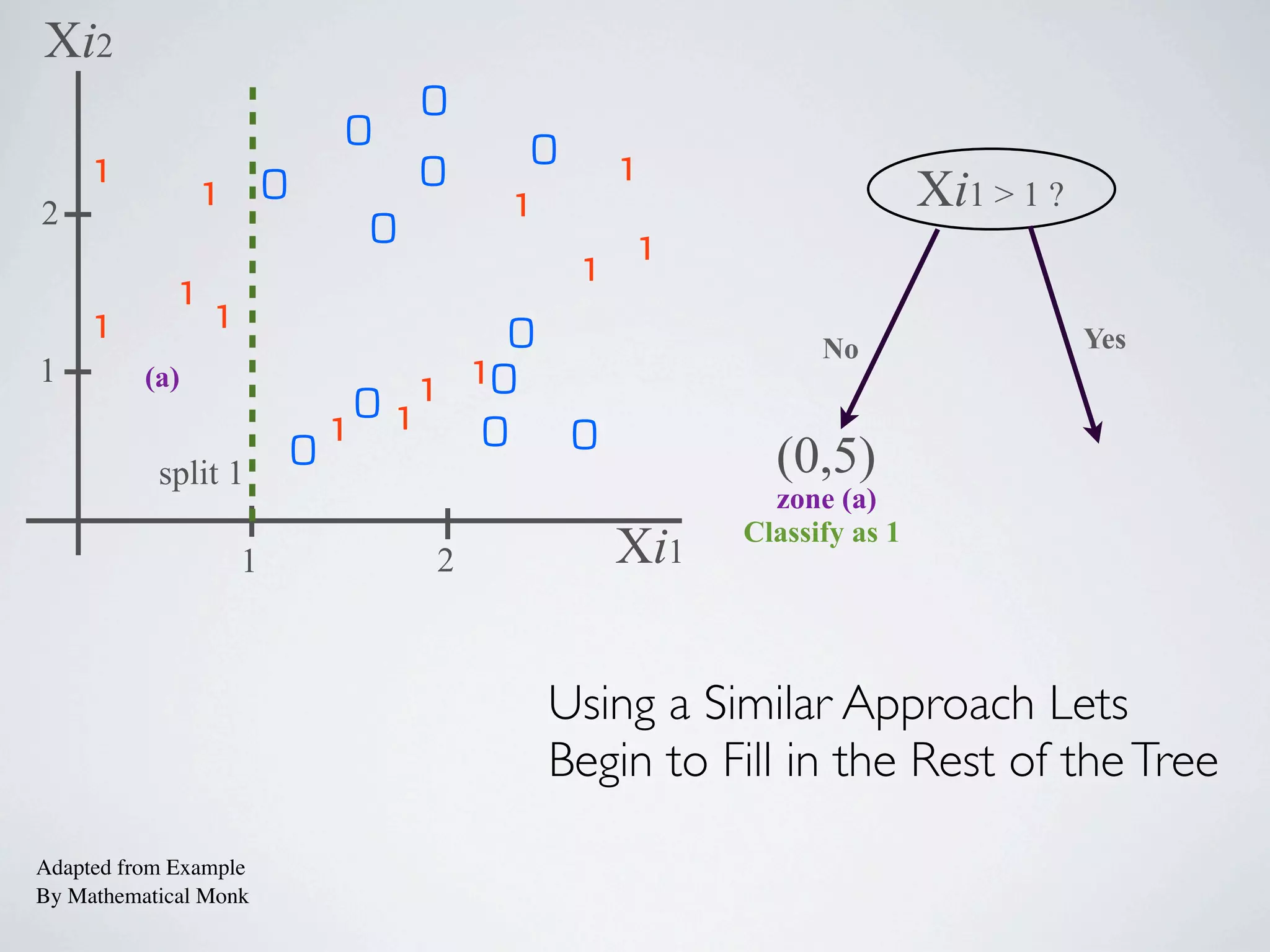
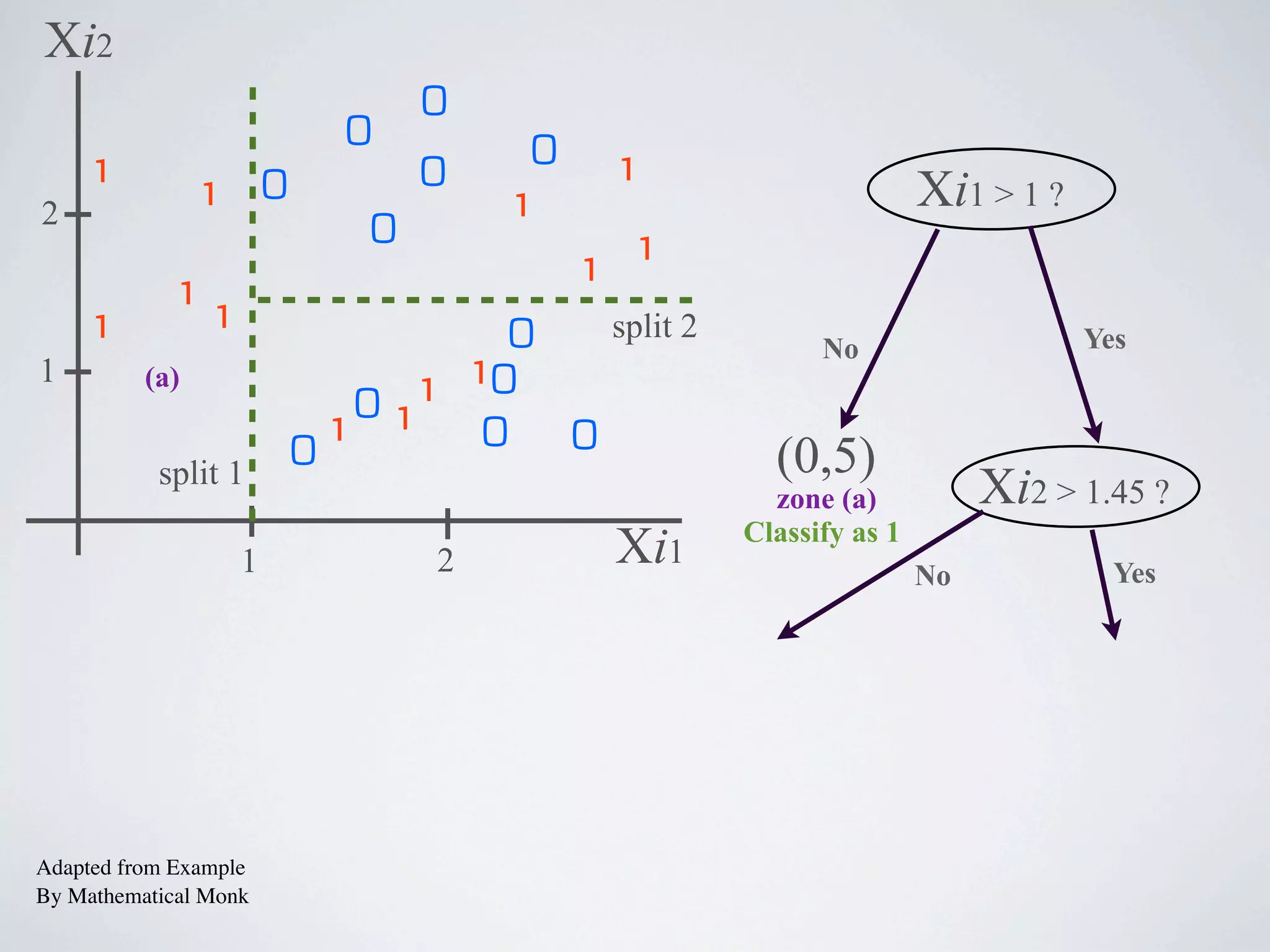
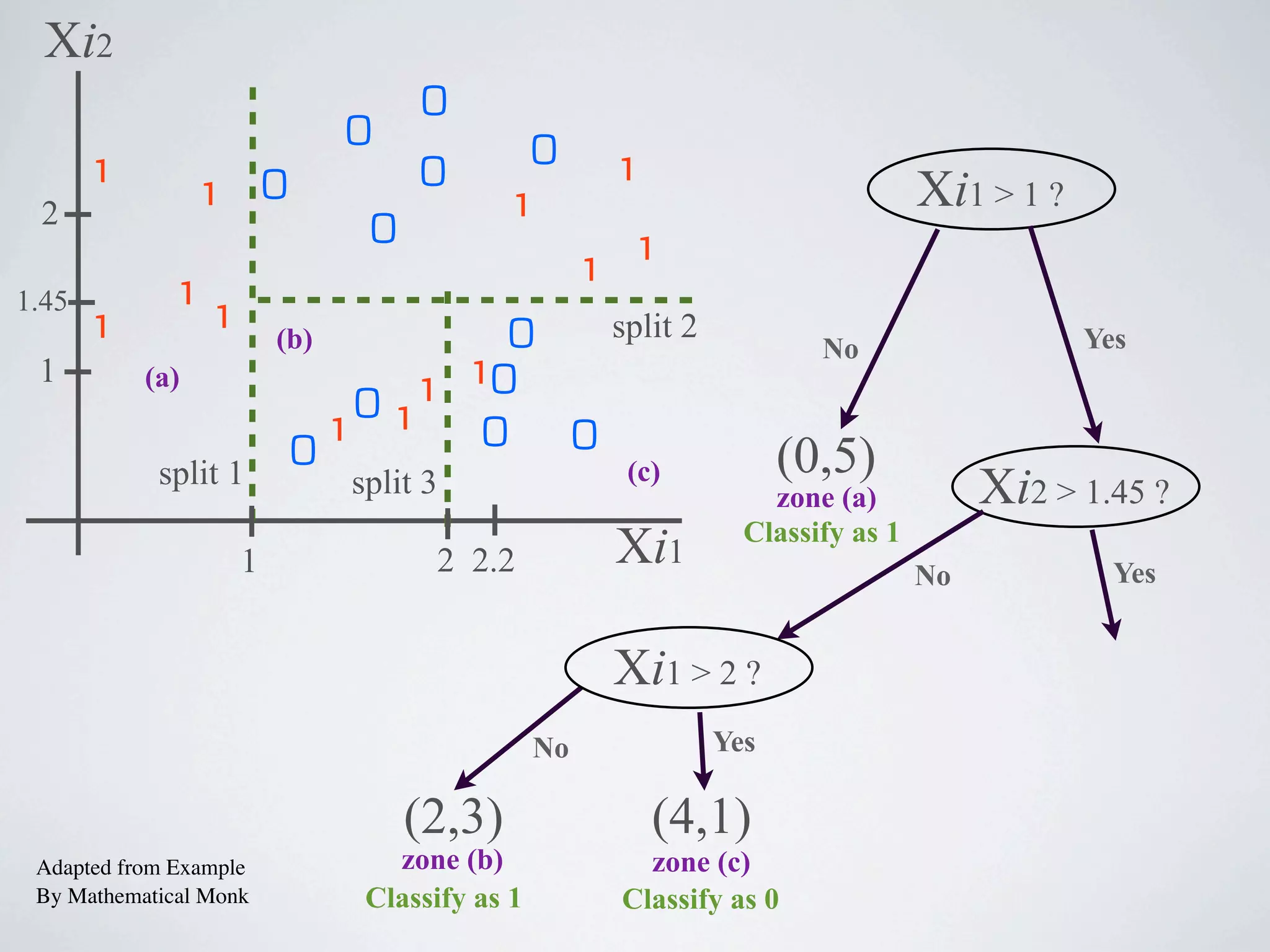
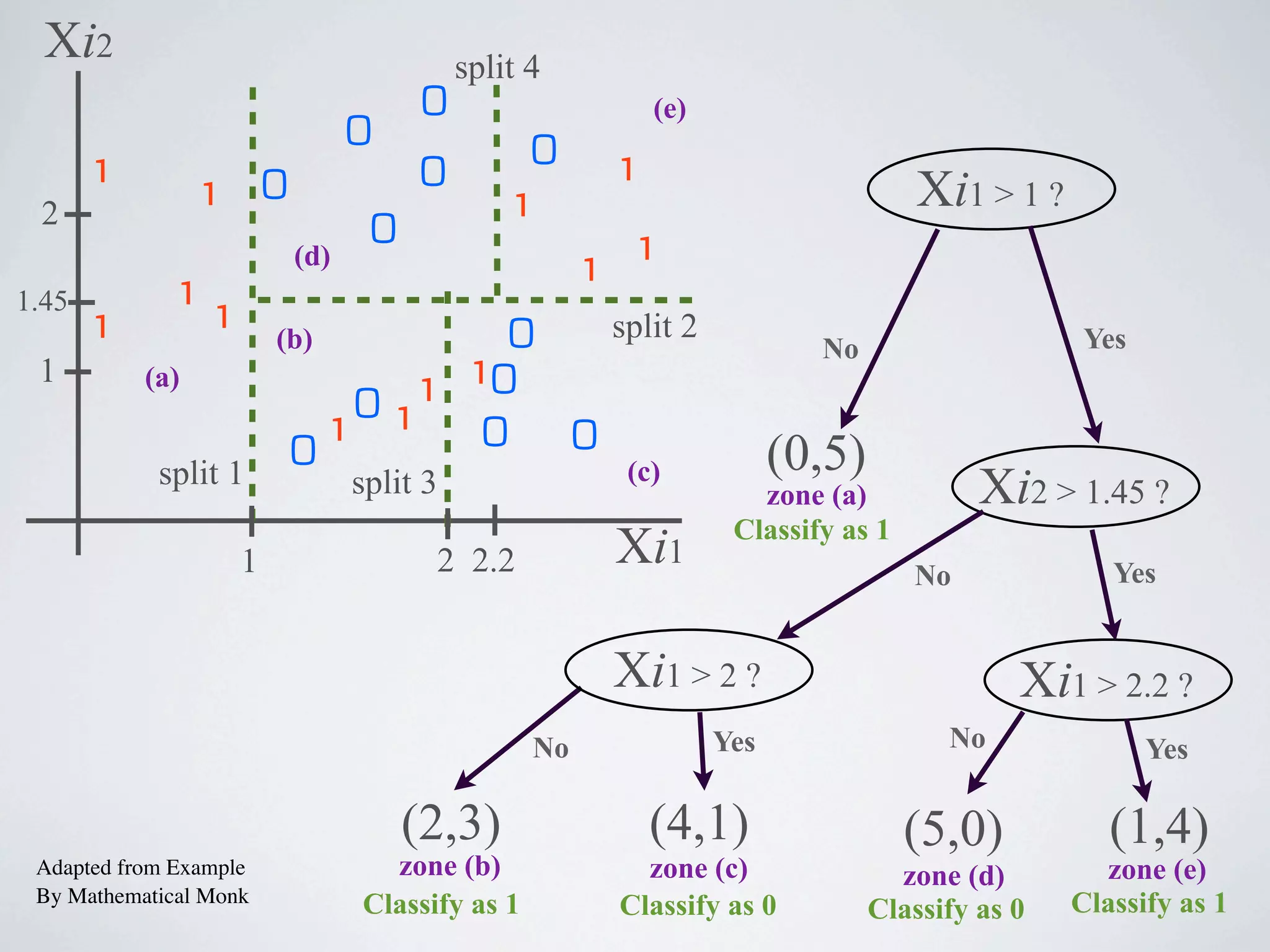
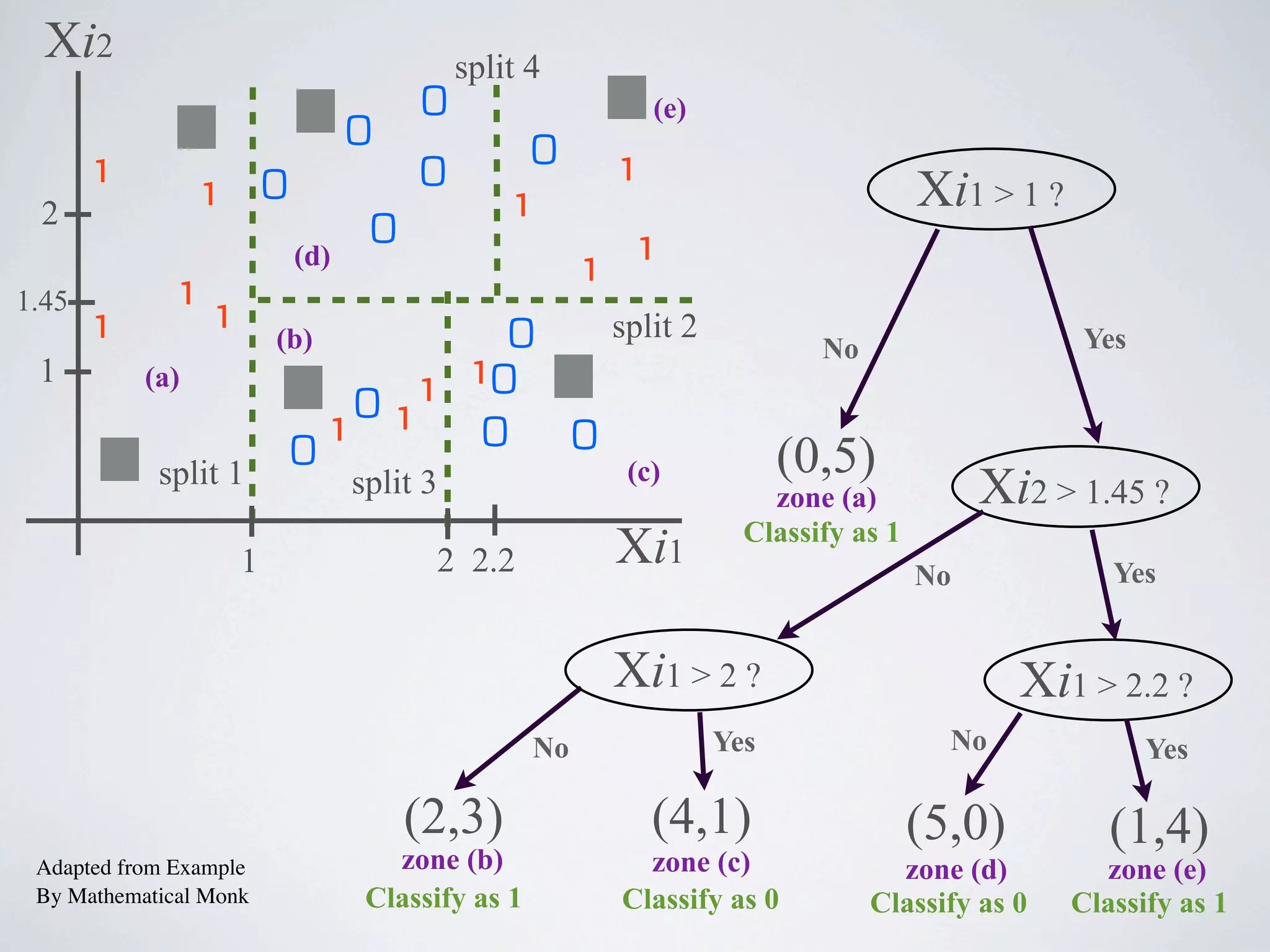
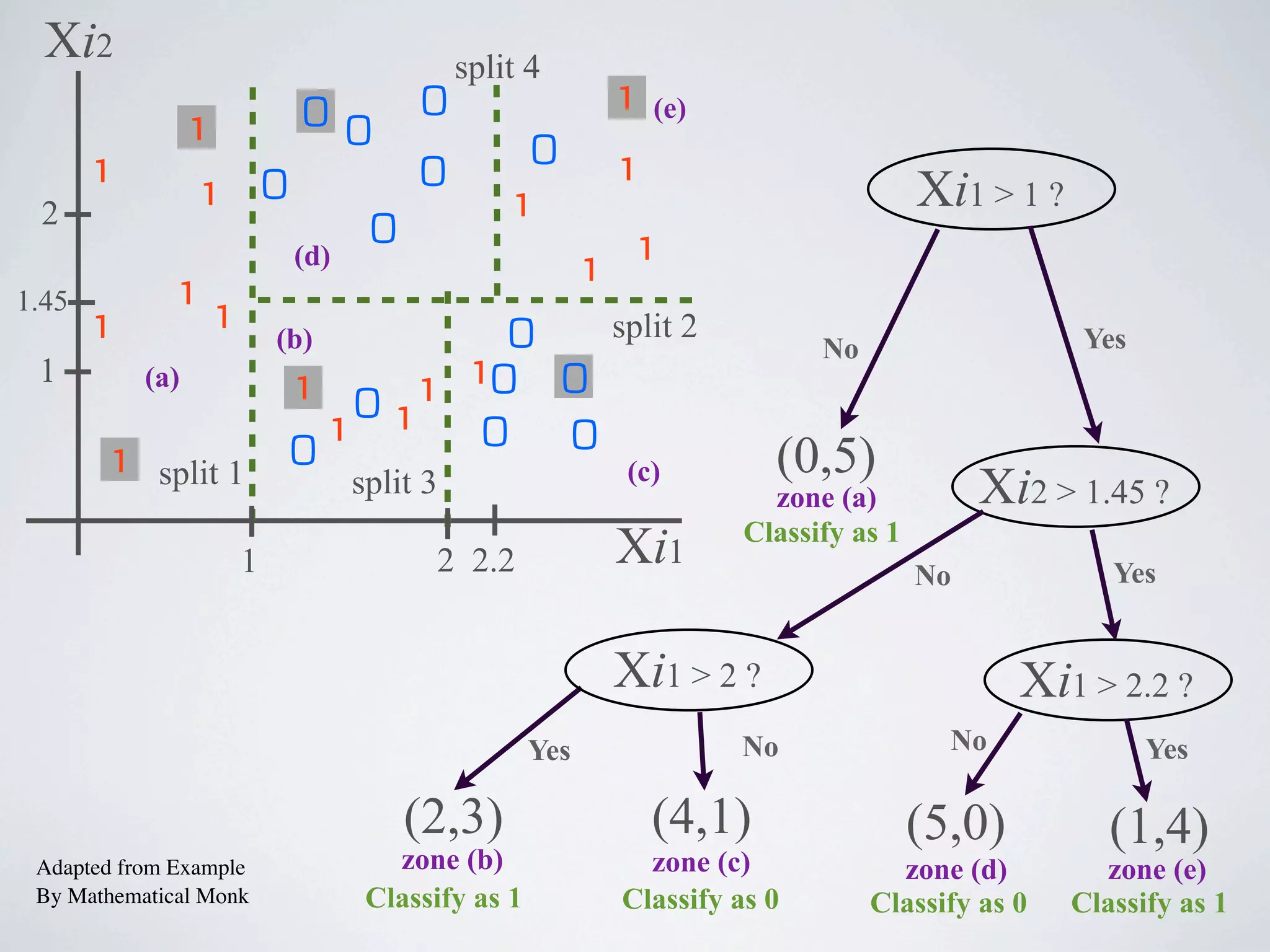
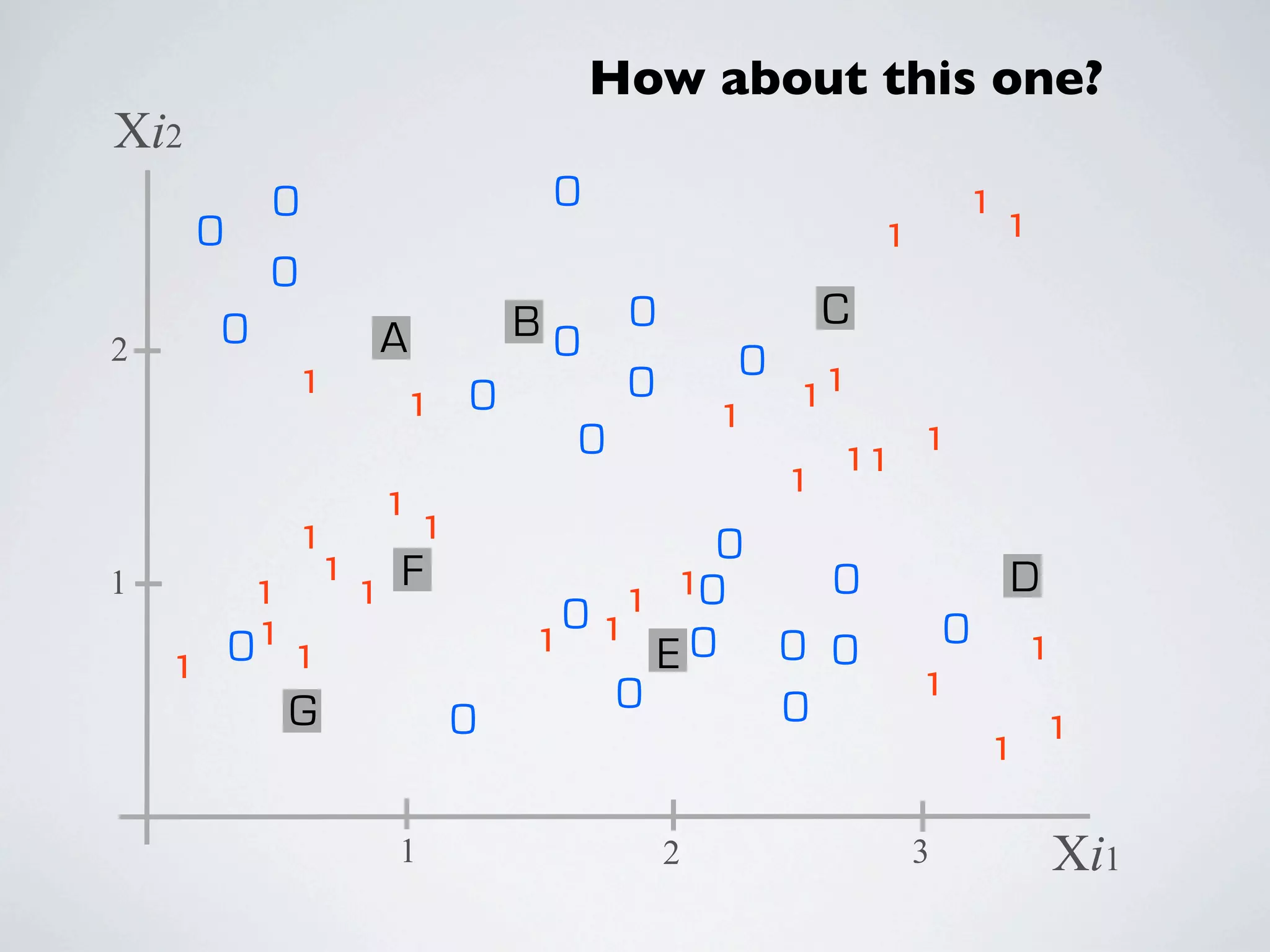
The document discusses binary classification and decision tree learning within the context of legal analytics, emphasizing supervised learning techniques and the use of decision trees for making predictions. It explains the methodology behind classification tasks, the greedy optimization approach used for tree-building, and the challenges associated with determining optimal partitions. Resources and additional learning materials related to this subject are also provided.