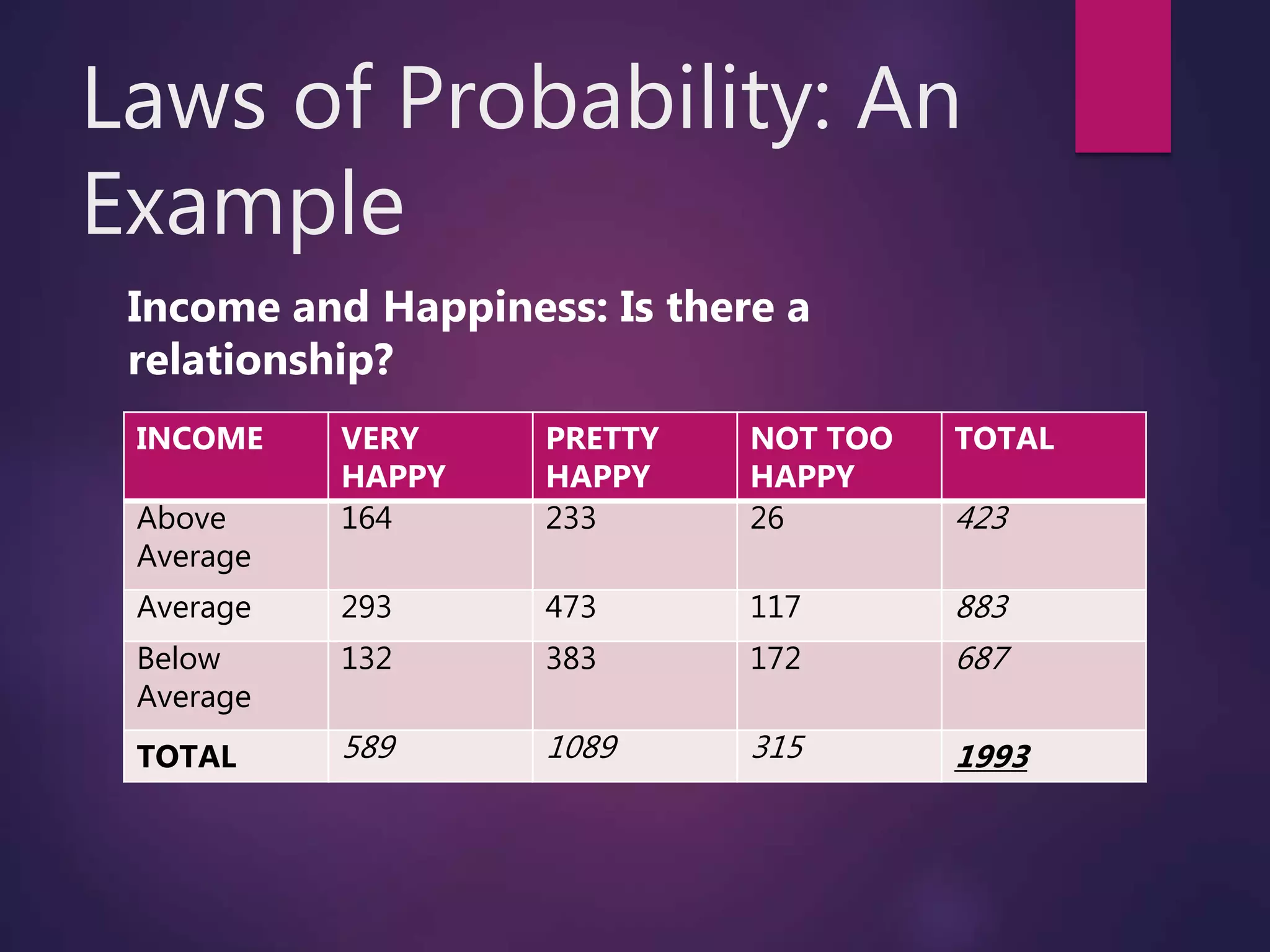
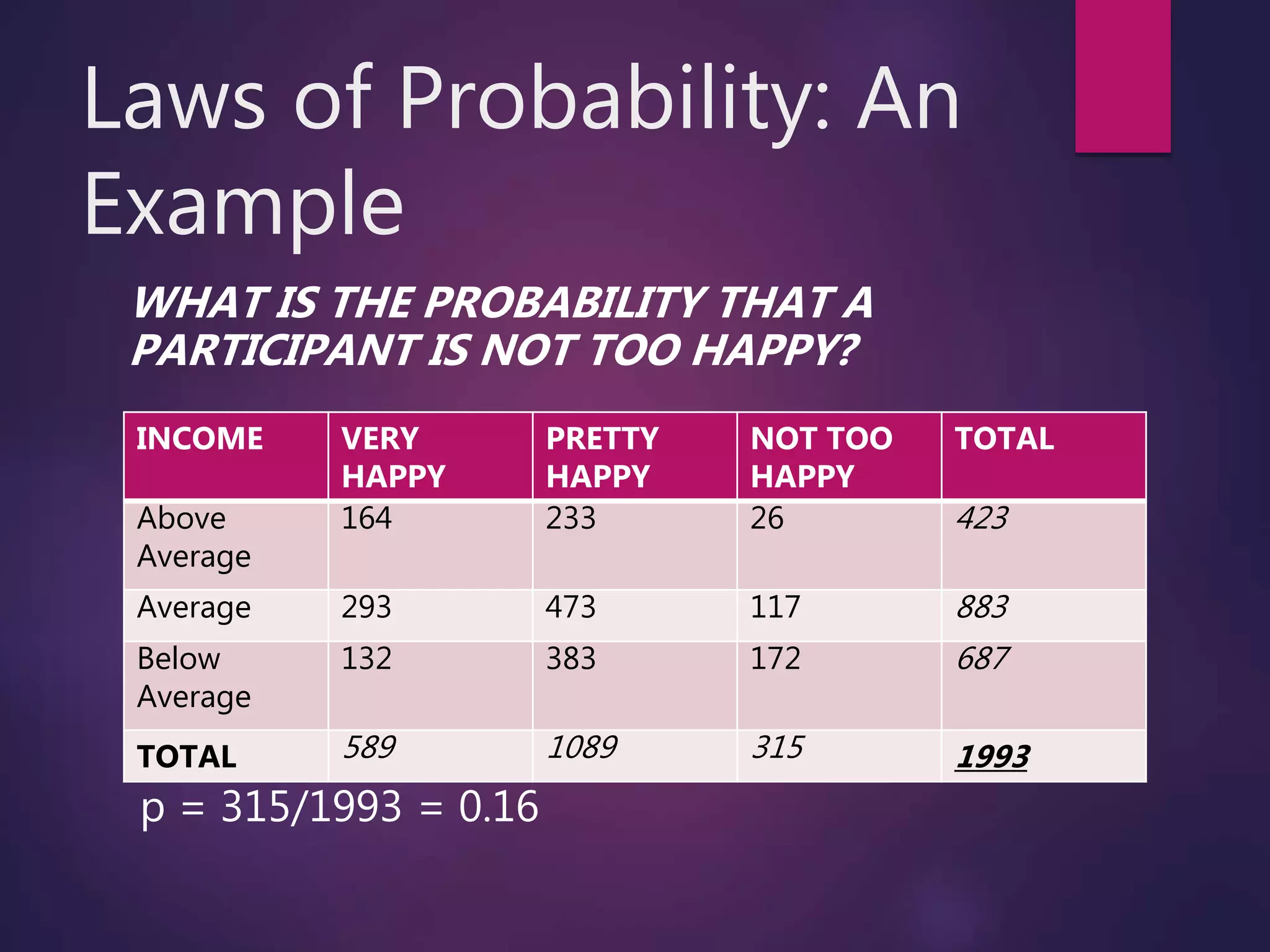
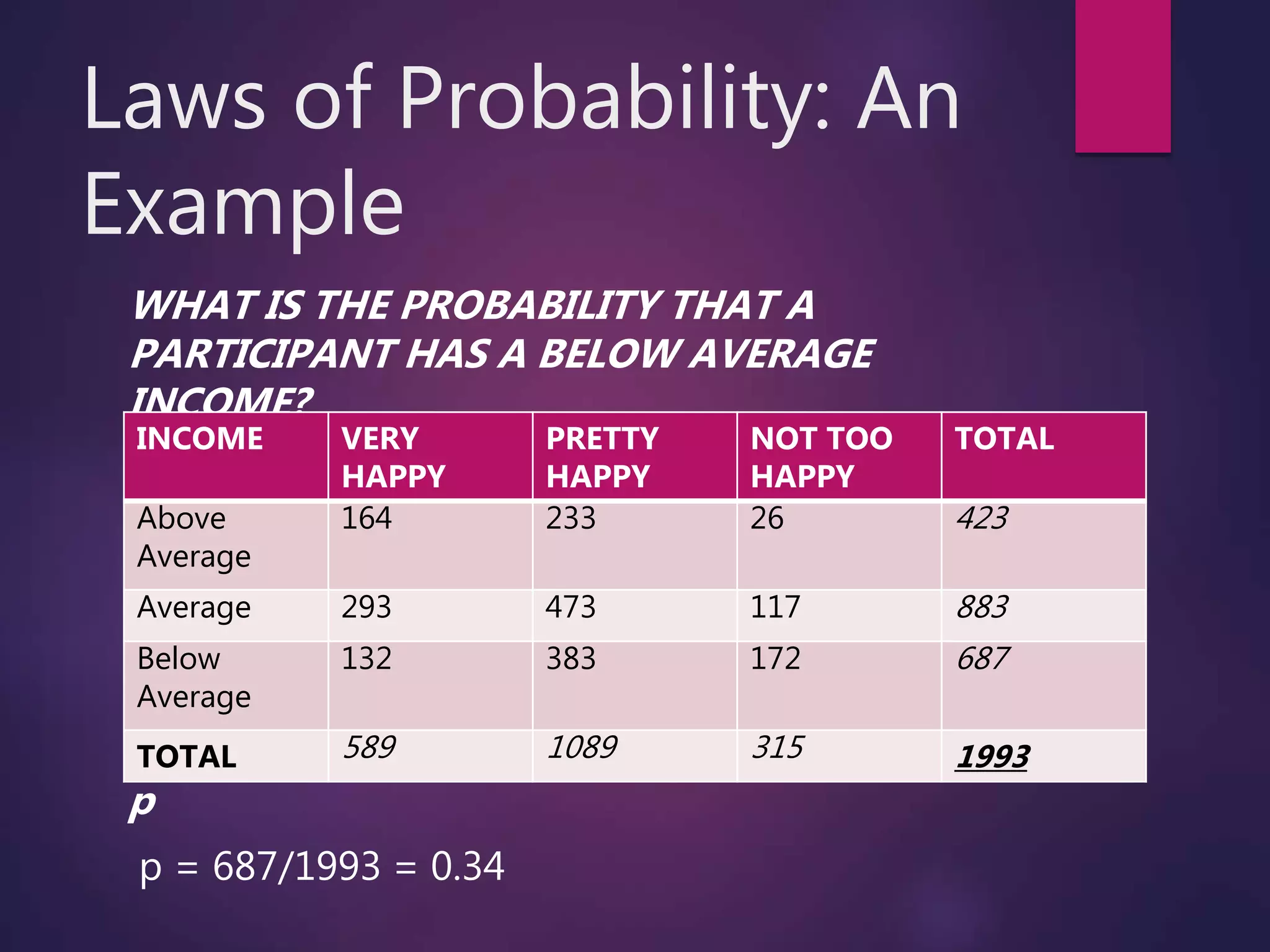
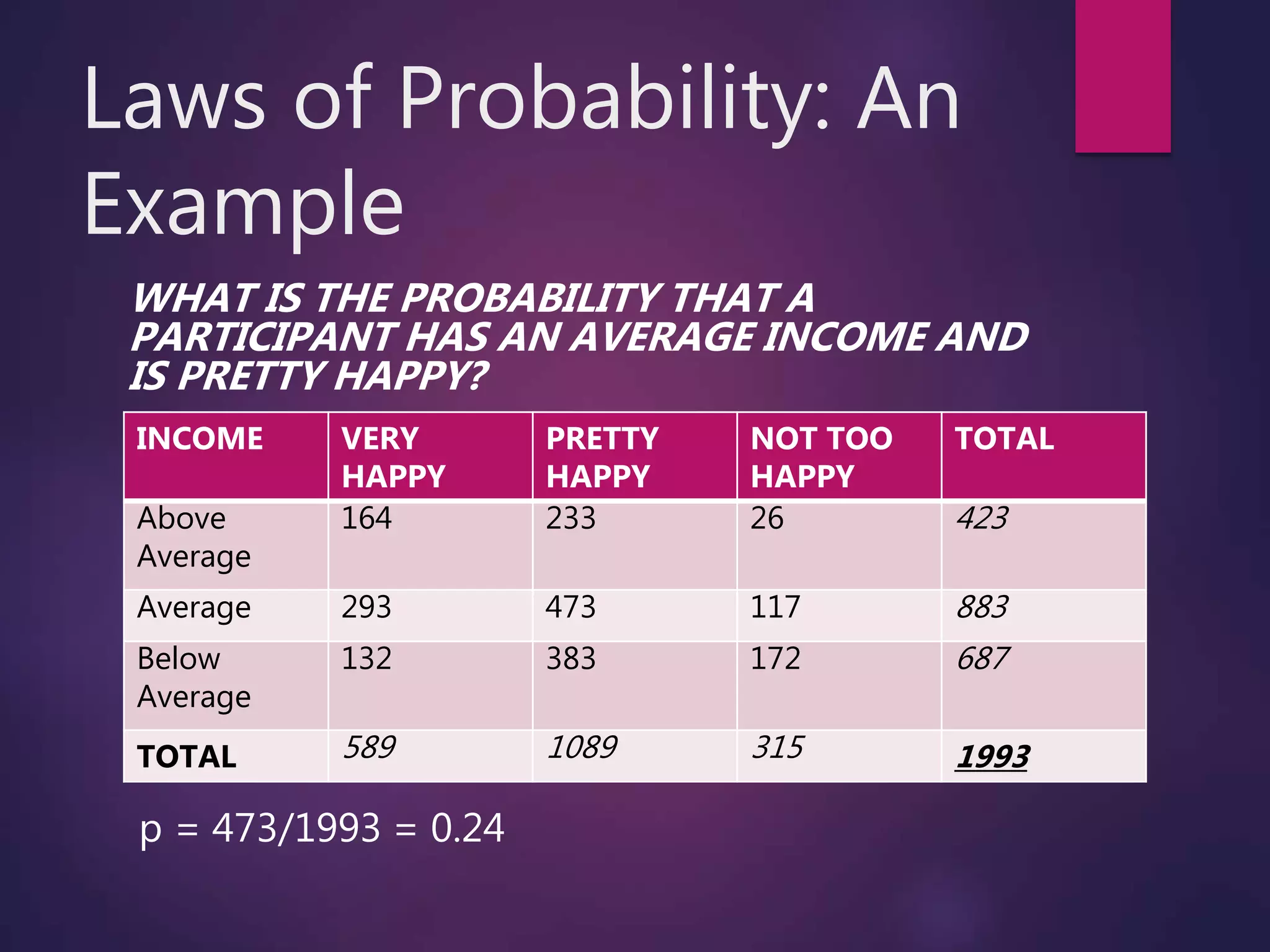
The document discusses key concepts in probability, including analytic, frequentist, and subjective views of probability. It covers terms like events, independence, dependent events, mutually exclusive events, and exhaustive events. Laws of probability like the additive law and multiplicative law are explained. Examples are provided to demonstrate calculating probabilities using tables and the normal distribution. The central limit theorem and law of large numbers are introduced.

1. Probability
&
Probability
Distribution

2. Analytic View of
Probability
 If an event can occur in A ways and can fail
to occur in B ways, and if all possible
outcomes are equally likely to occur, then:
 Occurrence:
 A/(A+B)
 Fail to Occur:
 B/(A+B)

3. Frequentist View of
Probability
 Probability is defined in terms of one’s past
performance
 Uses sampling with replacement/independent
random sampling

4. Subjective Probability
 An individuals subjective belief in the
likelihood of occurrence

5. Key Terms
• Data used in analyzing probability
• Outcome of trial
Event
• Occurrence of one event is not dependent on the other
Independent Events
• Outcome of one event is related to the other
Dependent Events
• One way only
Mutually Exclusive Events
• All possible events
Exhaustive Events

6. Laws of Probability
The probability of the occurrence of one event or another is equal
to the sum of their separate probabilities.
Additive Law
The probability of the joint occurrence of two or more
independent events is the product of their individual probabilities.
Multiplicative
Law
Co-occurrence of two events
Joint Probability
The probability that one event will occur given the occurrence of
some other event.
Conditional
Probability
The probability of one event ignoring the occurrence or
nonoccurrence of some other event.
Unconditional
Probability

7. Laws of Probability: An
Example
Income and Happiness: Is there a
relationship?
INCOME VERY
HAPPY
PRETTY
HAPPY
NOT TOO
HAPPY
TOTAL
Above
Average
164 233 26 423
Average 293 473 117 883
Below
Average
132 383 172 687
TOTAL 589 1089 315 1993

8. Laws of Probability: An
Example
WHAT IS THE PROBABILITY THAT A
PARTICIPANT IS NOT TOO HAPPY?
p
p = 315/1993 = 0.16
INCOME VERY
HAPPY
PRETTY
HAPPY
NOT TOO
HAPPY
TOTAL
Above
Average
164 233 26 423
Average 293 473 117 883
Below
Average
132 383 172 687
TOTAL 589 1089 315 1993

9. Laws of Probability: An
Example
WHAT IS THE PROBABILITY THAT A
PARTICIPANT HAS A BELOW AVERAGE
INCOME?
p
p = 687/1993 = 0.34
INCOME VERY
HAPPY
PRETTY
HAPPY
NOT TOO
HAPPY
TOTAL
Above
Average
164 233 26 423
Average 293 473 117 883
Below
Average
132 383 172 687
TOTAL 589 1089 315 1993

10. Laws of Probability: An
Example
WHAT IS THE PROBABILITY THAT A
PARTICIPANT HAS AN AVERAGE INCOME AND
IS PRETTY HAPPY?
p = 473/1993 = 0.24
INCOME VERY
HAPPY
PRETTY
HAPPY
NOT TOO
HAPPY
TOTAL
Above
Average
164 233 26 423
Average 293 473 117 883
Below
Average
132 383 172 687
TOTAL 589 1089 315 1993

11. Laws of Probability: An
Example
WHAT IS THE PROBABILITY THAT A
PARTICIPANT HAS A BELOW AVERAGE
INCOME GIVEN THAT HE/SHE IS VERY HAPPY?
p = 132/687 = 0.19
INCOME VERY
HAPPY
PRETTY
HAPPY
NOT TOO
HAPPY
TOTAL
Above
Average
164 233 26 423
Average 293 473 117 883
Below
Average
132 383 172 687
TOTAL 589 1089 315 1993

12. Laws of Probability: An
Example
WHAT IS THE PROBABILITY THAT A PARTICIPANT HAS A
BELOW AVERAGE INCOME AND IS NOT TOO HAPPY?
p = 687/1993 = 0.34
p = 315/1993 = 0.16
p = (0.34) x (0.16) = 0.05
INCOME VERY
HAPPY
PRETTY
HAPPY
NOT TOO
HAPPY
TOTAL
Above
Average
164 233 26 423
Average 293 473 117 883
Below
Average
132 383 172 687
TOTAL 589 1089 315 1993

13. The Normal Distribution
 Symmetrical
 Bell-shaped
 Mean, Median, and Mode are equal to one
another

14. The Normal Distribution

15. The Normal Distribution
 The use of z-scores can help determine the
probability
 Can describe the proportions of area
contained in each section of the distribution

16. The Normal Distribution
 The use of z-scores can help determine the
probability
 Can describe the proportions of area
contained in each section of the distribution

17. z-scores
 Helps identify the exact location of a score
in a distribution
 To make raw scores meaningful, they are
transformed into new values
 Standardizes the entire distribution

18. z-scores
𝑧 =
𝑥 − 𝑥
𝜎
𝑥 = 𝜇 + 𝑧𝜎

19. Example 1
SAT scores for a normal distribution with
mean of 500 and a standard deviation of 100.
What SAT score separates the top 10% of the
distribution from the test?

20. Solution 1
X = mean + (z) (sd)
X = 500 + (z) (100)
X = 500 + (1.28) (100)
X = 500 + 128
X = 628

21. Example 2
IQ test scores are standardized to produce a
normal distribution with a mean of 100 and a
standard deviation of 15. Find the proportion
of the population in each of the following IQ
categories:
Genius or near genius: IQ over 140
Very superior: IQ 120-140
Average: IQ 90-109

22. Solution 2
Genius or near genius:
z = 140-100/15
z = 2.67
p = 0.0038 or 3.8%
Very Superior:
z = 120-100/15 = 1.33
z = 140-100/15 = 2.67
p (120 < X < 140) = 0. 0918 – 0.0038
p = 0.0880 or 8.8%
Average:
z = 90-100/15 = -0.67
z = 109-100/15 = 0.60
p = (90 < X < 109) = 0.2486 + 0.2257
p = 0.4744 or 47.44%

23. Sampling Error
 Discrepancy between a sample statistic and
its corresponding population parameter
 If the population is normal, you should be
able to determine the probability of
obtaining any individual score

24. Sampling Distribution
 Distribution of statistics obtained by
selecting all the possible samples of a
specific size from a population

25. Distribution of Sample
Means
 Collection of sample means for all possible
random samples of a particular size that can
be obtained from a population
 Characteristics:
 Piles up around population mean
 Forms a normal distribution
 The larger the sample size, the closer to the
population mean

26. Central Limit Theorem
 For any population with mean and standard
deviation, the distribution of sample means
for sample size will have a mean and a
standard deviation ( 𝜎 𝑛) that will
approach a normal distribution as the
sample approaches infinity.

27. Central Limit Theorem
 Expected Value of M
 The mean of the distribution of sample
means is equal to the mean of the
population of scores
 Standard Error of M
 Provides a measure on how much distance is
expected between sample mean and population
mean

28. Law of Large Numbers
 The larger the sample size, the more
probable it is that the sample mean will be
close to the population mean
 When n > 30, the distribution is almost
normal regardless of the shape
 As sample size increases, error decreases