Uploaded byDaniel Katz
Quantitative Methods for Lawyers - Class #20 - Regression Analysis - Part 3
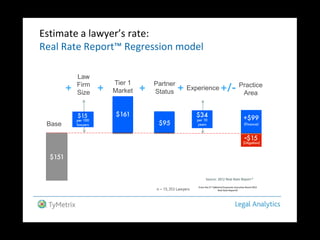
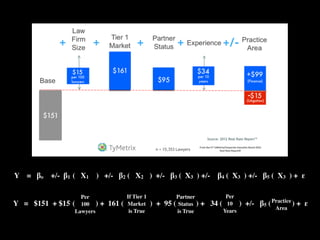
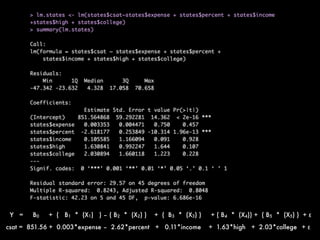
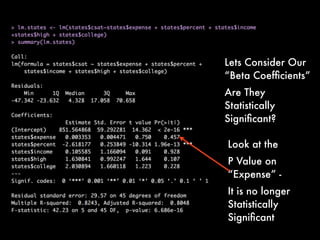
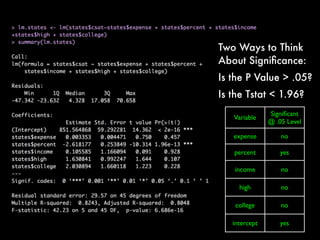
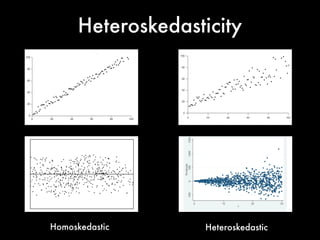
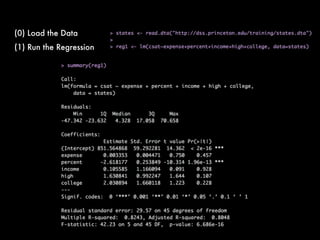
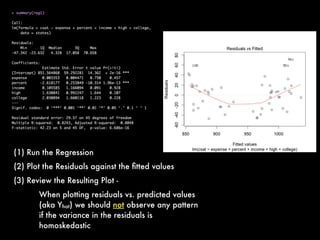
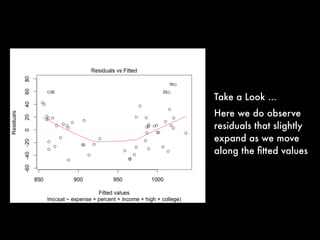
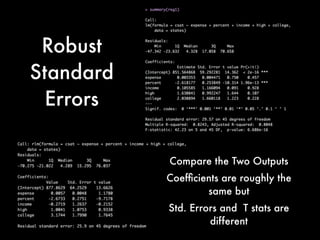
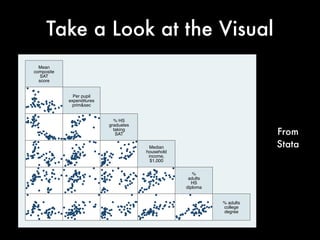
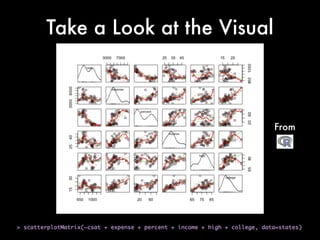
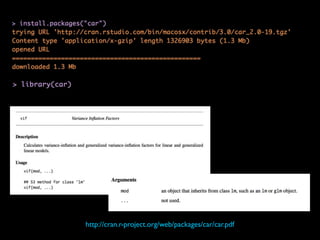
This document discusses multiple regression analysis and some key assumptions and issues that can arise. It provides an example of using multiple regression to estimate SAT scores based on various state-level factors like expenditures, income levels, education levels etc. It discusses how to detect issues like heteroskedasticity and multicollinearity that can violate the assumptions of regression analysis. It demonstrates how to use robust standard errors to account for heteroskedasticity and examines variance inflation factors to check for multicollinearity issues.
More Related Content
Similar to Quantitative Methods for Lawyers - Class #20 - Regression Analysis - Part 3
Quantitative Methods for Lawyers - Class #20 - Regression Analysis - Part 3
- 1. Quantitative Methods for Lawyers Class #20 RegressionAnalysis Part 3 @ computational computationallegalstudies.com professor daniel martin katz danielmartinkatz.com lexpredict.com slideshare.net/DanielKatz
- 2.
- 3.
- 4. Keep This VisualImage in Your Mind
- 5. Estimate a lawyer’srate: Real Rate Report™ Regression model From the CT TyMetrix/Corporate Executive Board 2012 Real Rate Report© $15 1 $16 1 $34 per 10 years$95 +$99 (Finance) -$15 (Litigation) n = 15,353 Lawyers Tier 1 Market Experience Partner Status Practice Area Base + + +/- Source: 2012 Real Rate Report™ 32 $15 Per 100 Lawyers Law Firm Size+ + $161 $151 $15 per 100 lawyers $95 $34 per 10 years -$15 (Litigation) +$99 (Finance)
- 6. Y = βo+/- β1 ( X1 ) +/- β2 ( X2 ) +/- β3 ( X3 ) +/- β4 ( X3 ) +/- β5 ( X3 ) + ε Y = $151 + $15 ( ) + 161 ( ) + 95 ( ) + 34 ( ) +/- β5 ( ) + ε Per 100 Lawyers If Tier 1 Market is True Partner Status is True Per 10 Years Practice Area
- 7. From The LastTime...
- 8. Now Lets Considerthe More Complex Case: Relationship Between Sat Score and Expenditures/ Variety of other Variables ? Our Y Dependent Variable Our X Predictors/ Independent Variables Multivariate Regression
- 9. Y = B0+ ( B1 * (X1) ) – ( B2 * (X2) ) + ( B3 * (X3) ) + ( B4 * (X4)) + ( B5 * (X5) ) + ε csat = 851.56 + 0.003*expense – 2.62*percent + 0.11*income + 1.63*high + 2.03*college + ε
- 10. Lets Consider Our “BetaCoefficients” Are They Statistically Significant? Look at the P Value on “Expense” - It is no longer Statistically Significant
- 11. Two Ways toThink About Significance: Is the P Value > .05? Is the Tstat < 1.96? Variable Significant @ .05 Level expense no percent yes income no high no college no intercept yes
- 12. Using Our Modelto Predict
- 13. Using Our Modelto Predict What if we had a Hypothetical State with the following factors - • Per Pupil Expenditures Primary & Secondary (expense) - $6000 • % HS of graduates taking SAT (percent) - 20% • Median Household Income (income) - 33.000 • % adults with HS Diploma (high) - 70% • % adults with College Degree (college) - 15% • Midwest State (Region=South) Please Predict the Mean Score for this Hypothetical State? Here is our Model: csat = 849.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε
- 14. Using Our Modelto Predict What if we had a Hypothetical State with the following factors - • Per Pupil Expenditures Primary & Secondary (expense) - $6000 • % HS of graduates taking SAT (percent) - 20% • Median Household Income (income) - 33.000 • % adults with HS Diploma (high) - 70% • % adults with College Degree (college) - 15% • Midwest State (Region=South) Here is our Model: csat = 849.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε csat = 849.59 – 0.002*(6000) – 3.01*(20) – 0.17*(33.000) + 1.81*(70) + 4.67*(15) + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε
- 15. Using Our Modelto Predict csat = 849.59 – 0.002*(6000) – 3.01*(20) – 0.17*(33.000) + 1.81*(70) + 4.67*(15) + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε csat = 849.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε csat = 849.59 – 12 – 60.2 – 5.61 + 126.7 + 70.05 + - 9.18 predicted composite SAT Score = 959.35
- 16.
- 17. Heteroskedasticity Regression Analysis assumesthat error terms are independently, identically and normally distributed Assumes that error terms have mean of zero and a constant variance (i.e. variance is the same throughout all subsets of values of the error terms) What does this Mean? If there is an error in our estimate - that estimate is still centered around the true variable value No Systematic Error in over/under estimating the regression coefficients
- 18. Heteroskedasticity Heteroscedasticity does notcause ordinary least squares coefficient estimates to be biased, although it can cause ordinary least squares estimates of the variance (and, thus, standard errors) of the coefficients to be biased, possibly above or below the true or population variance. Thus, regression analysis using heteroscedastic data will still provide an unbiased estimate for the relationship between the predictor variable and the outcome, but standard errors and therefore inferences obtained from data analysis are suspect. Biased standard errors lead to biased inference, so results of hypothesis tests are possibly wrong.
- 19.
- 20. How Do IDetect Heteroskedasticity? Visual (Ocular) Method is a good starting point (although you should probably also check with a more formal approach) However, lets just start here: (1) Run the Regression (2) Plot the Residuals against the fitted values (3) Review the Resulting Plot - When plotting residuals vs. predicted values (aka Yhat) we should not observe any pattern if the variance in the residuals is homoskedastic
- 21. (0) Load theData (1) Run the Regression
- 22. (1) Run theRegression (2) Plot the Residuals against the fitted values (3) Review the Resulting Plot - When plotting residuals vs. predicted values (aka Yhat) we should not observe any pattern if the variance in the residuals is homoskedastic
- 23. Take a Look... Here we do observe residuals that slightly expand as we move along the fitted values
- 24. How Do IDetect Heteroskedasticity? There is a More Formal Approach ... the Breusch-Pagan test Test the Null Hypothesis of Constant Variance (1) Run the Regression (2) Execute the Breusch-Pagan test
- 25. How Do IDetect Heteroskedasticity? However, it is generally considered wise to use assume Heteroskedasticity and control for it in an appropriate manner This is a Fail to Reject Situation
- 26.
- 27. Robust Standard Errors RobustStandard Errors Control for heteroskedasticity In R you can just use “rlm” instead of “lm”
- 28. Robust Standard Errors Compare the TwoOutputs Coefficients are roughly the same but Std. Errors and T stats are different
- 29.
- 30. Multicollinearity statistical phenomenon inwhich two or more predictor variables in a multiple regression model are highly correlated. In this situation the coefficient estimates may change erratically in response to small changes in the model or the data. Multicollinearity does not reduce the predictive power or reliability of the model as a whole, at least within the sample data themselves; it only affects calculations regarding individual predictors.
- 31. Take a Lookat the Visual Mean composite SAT score Per pupil expenditures prim&sec % HS graduates taking SAT Median household income, $1,000 % adults HS diploma % adults college degree From Stata
- 32. Take a Lookat the Visual From R
- 33. Take a Lookat the Visual Mean composite SAT score Per pupil expenditures prim&sec % HS graduates taking SAT Median household income, $1,000 % adults HS diploma % adults college degree
- 34.
- 35. How Do IDetect Multicollinearity? (1) Run the Regression (2) Obtain and then Examine the Variance Inflation Factor (“VIF”) A vif > 10 or a 1/vif < 0.10 is an issue Here we look to be okay
- 36. Daniel Martin Katz @computational computationallegalstudies.com lexpredict.com danielmartinkatz.com illinois tech - chicago kent college of law@