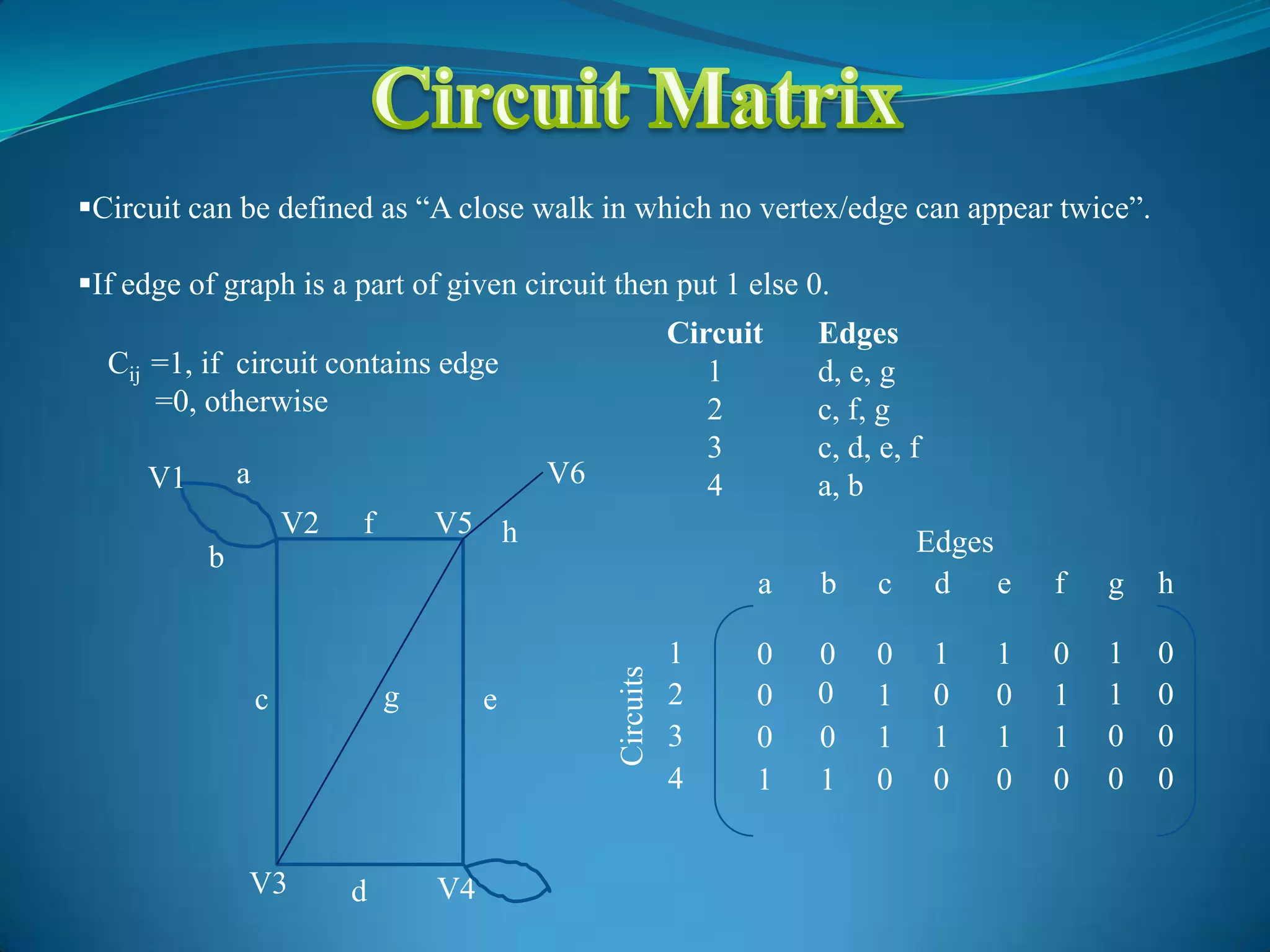
The document discusses different matrix representations of graphs: 1) Incidence matrix shows which edges are incident to each vertex with 1s and 0s. 2) Adjacency matrix shows which vertices are adjacent to each other with 1s and 0s. 3) Cut-set matrix shows which edges are part of given cut sets that disconnect the graph with 1s and 0s.

1. Presented By:
Abhishek Pachisia
B.Tech-IT(V Sem)
090102801

2. Graph is a set of edges and vertices.
Graph can be represented in the form of matrix.
Different matrix that can be formed are:
1. Incidence Matrix
2. Adjacency Matrix
3. Cut-Set Matrix
4. Circuit Matrix
5. Path Matrix

3. Edge connected to the vertex is known as incidence edge to that vertex.
If vertex is incident on vertex then put 1 else 0. Vertex Edges
1 a, b
2 a, b, c, f
aij =1, if edge ej is incident on vertex vi 3 c, d, g
=0, otherwise 4 d, e
5 d, e, f, g, h
6 h
V1 a V6
V2 f V5 h
b Edges
a b c d e f g h
V1 1 1 0 0 0 0 0 0
V2 1 1 1 0 0 1 0 0
Vertex
c e V3 0 0 1 1 1 0 1 0
V4 0 0 0 1 1 0 1 0
V5 0 0 0 1 1 1 1 1
V6 0 0 0 0 0 0 0 1
V3 d V4

4.  If two vertices are connected by single path than they are known as adjacent vertices.
 If vertex is connected to itself then vertex is said to be adjacent to itself.
If vertex is adjacent then put 1 else 0.
V1 a V6
V2 f V5 h Vertices
b V1 V2 V3 V V5 V6
4
V1 0 1 0 0 0 0
V2 1 0 1 0 1 0
Vertices
c e V3 0 1 0 1 1 0
V4 0 0 1 1 1 0
V5 0 1 1 1 0 1
V6 0 0 0 0 0 1
V3 d V4

5. Cut set is a “Set of edges in a graph whose removal leaves the graph disconnected”.
If edge of graph is a part of given cut set then put 1 else 0.
Cut Set Edges
Cij =1, if jth
cutset contains edge 1 f, g, d
=0, otherwise 2 c, g, e
3 h
V1 a V6 4 a, b
V2 f V5 h
b Edges
a b c d e f g h
1 0 0 0 1 0 1 1 0
Cut Sets
c e 2 0 0 1 0 1 0 1 0
3 0 0 0 0 0 0 0 1
4 1 1 0 0 0 0 0 0
V3 d V4

6. Circuit can be defined as “A close walk in which no vertex/edge can appear twice”.
If edge of graph is a part of given circuit then put 1 else 0.
Circuit Edges
Cij =1, if circuit contains edge 1 d, e, g
=0, otherwise 2 c, f, g
3 c, d, e, f
V1 a V6 4 a, b
V2 f V5 h
b Edges
a b c d e f g h
1 0 0 0 1 1 0 1 0
Circuits
c e 2 0 0 1 0 0 1 1 0
3 0 0 1 1 1 1 0 0
4 1 1 0 0 0 0 0 0
V3 d V4

7. Path can be defined as “A open walk in which no vertex/edge can appear twice”.
If edge of graph is a part of given path then put 1 else 0. Path Edges
1 a, f, h
P( Vj,Vi)=1,if edge is on path Ex: P ( V1,V6) 2 a, c, g, h
=0, otherwise 3 a, c, d, e, h
4 b, f, h
V1 a V6 5 b, c, g, h
6 b,c, d, e, h
V2 f V5 h Edges
b
a b c d e f g h
1 1 0 0 0 0 1 0 1
0
Paths
c e 2 1 1 0 0 0 1 1
3 1 0 1 1 1 0 0 1
4 0 1 0 0 0 1 0 1
5 0 1 1 0 0 0 1 1
6 0 1 1 1 1 0 0 1
V3 d V4