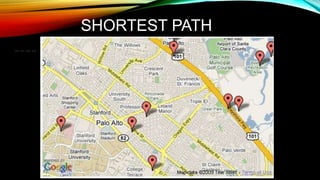
This document provides information about adjacency and incidence matrices used to represent graphs. It defines what a graph is consisting of edges and vertices. Adjacency and incidence matrices are introduced as ways to represent graphs mathematically. The differences between directed and undirected adjacency matrices are explained. An example of each is shown with a graph. Incidence matrices are also defined showing the relationship between vertices and edges. The document concludes with applications of converting between these matrix representations and using them to find the shortest path.

1. CSE 131: DISCRETE MATHEMATICS
MS. TASMIA TASRIN ( LECTURER )
Group: Enigma
H.M. Rafi Hasan (161-15-7050)
Mohammad Touhidul Islam (161-15-7051)
Md. Rahmat Ullah (161-15-6970)
Abir Hasnat (161-15-6789)
Alinewaz Chowdhory (161-15-6790)

2. PRESENTATION ON
Adjacency And Incidence Matrix

3. WHAT IS GRAPH?
Graph is a set of edges and vertices.
A B
C D
E

4. REPRESENTING OF GRAPHS
Graph can be represented in the form of matrix.
Different matrix that can be formed are:
1. Adjacency Matrix
2. Incidence Matrix
3. Cut-Set Matrix
4. Circuit Matrix
5. Path Matrix

5. Adjacency Matrix
Edge connected to the vertex is known as incidence edge to that vertex
 If vertex is connected to itself then vertex is said to be adjacent to itself.
If vertex is adjacent then put 1 else 0.
Undirected and directed adjacency matrix is different
a
V6
V4
V5V2
V3
h
ec
f
d
V1 a
b
0 00
0 01
1 01
1 01
1 10
0 10
0 10
0 11
0 00
0 02
2 1
0 01
0
V4 V6V5V1 V3V2
V1
V2
V3
V4
V5
V6
Vertices
Vertices

6. DIRECTED ADJACENCY MATRIX
V6
V4
V5V2
V3
h
ec
f
d
V1
a
b
0 00
0 01
0 01
1 00
1 10
0 00
0 10
0 00
0 00
0 01
1 1
0 00
0
V4 V6V5V1 V3V2
V1
V2
V3
V4
V5
V6
Vertices
Vertices

7. Incidence Matrix
Edge connected to the vertex is known as incidence edge to that vertex
If vertex is incident on vertex then put 1 else 0.
V6
V4
V5V2
V3
h
ec
f
d
V1 a
b
Vertex
V1
V2
V3
V4
V5
V6
Edges
a, b
a, b, c, f
c, d, g
d, e
d, e, f, g, h
h
0 00
0 10
1 01
1 010 00
1 01
1 1
0 10
1
d fea cb
V4
V1
V
2V3
g h
0
0
1
1
0
0
0
0
Edges
Vertex
1 11
0 000 00
0 00
V6
V5 1
0
1
1

8. APPLICATION OF INCIDENCE
AND ADJACENCY MATRIX

9. INCIDENCE TO ADJACENCY MATRIX
• int m = 4; // number or rows = number of cols
• double mat[m][m] = {
• {0, 1, 1, 1} , // first point adjacent to all others
• {1, 0, 0, 0} , // 2nd only adjacent to 1st
• {1, 0, 0, 1} , // 3rd adjacent to 1st & 4th
• {1, 0, 1, 0} // 4th adjacent to 1st & 3rd
• };
•
• for(int i=0; i<m-1;++i)
• {
• for(int j=i+1; j < m; ++i)
• { // loop through upper triangle
• if( math[i][j] )
• { // if element is set
• addPair(i,j); // add it to the list
• }
• }
• }

10. MAPPING

11. •Adjacency Lists and average time complexity
for binary search

12. SHORTEST PATH

14. GOOGLE SELF-DRIVING CAR