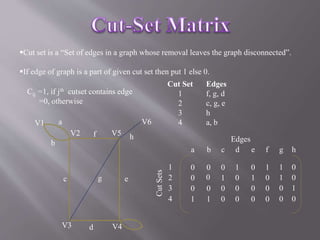
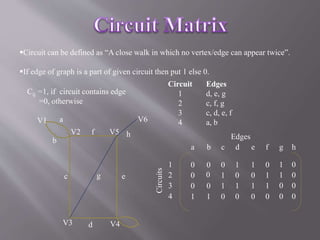
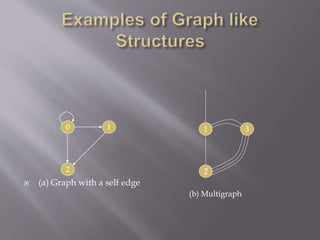
The document discusses different ways to represent graphs using matrices. It describes incidence matrices, adjacency matrices, cut-set matrices, circuit matrices, and path matrices. Each matrix represents the connections between vertices and edges in a graph. The document provides examples of defining the elements in each matrix type based on whether an edge is incident to, adjacent to, part of a cut-set, circuit, or path between two vertices.

1. Presented By:
KESHAV SOMANI
BBA(E-COMM)IIISEM.
ROLLNO.56417

2. MATRIX REPRESENTATION
OF GRAPH

3. Graph is a set of edges and vertices.
Graph can be represented in the form of matrix.
Different matrix that can be formed are:
1. Incidence Matrix
2. Adjacency Matrix
3. Cut-Set Matrix
4. Circuit Matrix
5. Path Matrix

4. Edge connected to the vertex is known as incidence edge to that vertex.
If vertex is incident on vertex then put 1 else 0.
aij =1, if edge ej is incident on vertex vi
V6
f
=0, otherwise
V2 V5
V4
V3
h
c e
d
V1 a
b
a b c d e f
0 0 0
0 0 1
1 1 0
1 1 0
1 1
1
0 0 1
0 0 0 1 1 0
V1
V2
V3
V4
g h
0
0
0
0
1
0
1
0
Edges
Vertex
V5 1
1 1 1
0 0 0
0 0 0 0 0 0
V6
0
1
1
Vertex
1
2
3
4
5
6
Edges
a, b
a, b, c, f
c, d, g
d, e
d, e, f, g, h
h

5.  If two vertices are connected by single path than they are known as adjacent vertices.
 If vertex is connected to itself then vertex is said to be adjacent to itself.
If vertex is adjacent then put 1 else 0.
V6
f
V2 V5
V4
V3
h
c e
d
V1 a
b
V1 V2 V3 V5 V6
0 0 0
0 1 0
1 1 0
1 1 0
1 0 1
0 0 1
0 1 0
1 0
1
0 1 0
0 0 1
0 1 1
0 0 0
V
4
V1
V2
V3
V4
V5
V6
Vertices
Vertices

6. Cut set is a “Set of edges in a graph whose removal leaves the graph disconnected”.
If edge of graph is a part of given cut set then put 1 else 0.
V6
V2 V5
V4
V3
h
f
c e
d
V1 a
b
a b c d e f
1 0 1
0 1 0
0 0 0
0 0 0
0 0
1
0 0 0
1 1 0 0 0 0
1
2
3
4
g h
1
1
0
0
0
0
1
0
Edges
Cut Sets
Cut Set
1
2
3
4
Edges
f, g, d
c, g, e
h
a, b
Cij =1, if jth cutset contains edge
=0, otherwise

7. Circuit can be defined as “A close walk in which no vertex/edge can appear twice”.
If edge of graph is a part of given circuit then put 1 else 0.
V6
V2 V5
V4
V3
h
f
c e
d
V1 a
b
a b c d e f
1 1 0
0 0 1
1 1 1
0 0 0
0 0
1
0 0 1
1 1 0 0 0 0
1
2
3
4
g h
1
1
0
0
0
0
0
0
Edges
Circuits
Circuit
1
2
3
4
Edges
d, e, g
c, f, g
c, d, e, f
a, b
Cij =1, if circuit contains edge
=0, otherwise

8. Path can be defined as “A open walk in which no vertex/edge can appear twice”.
If edge of graph is a part of given path then put 1 else 0. Path
V6
V2 V5
V4
V3
h
f
c e
d
V1 a
b
1
2
3
4
5
6
Edges
a, f, h
a, c, g, h
a, c, d, e, h
b, f, h
b, c, g, h
b,c, d, e, h
P( Vj,Vi)=1,if edge is on path
=0, otherwise
Ex: P ( V1,V6)
a b c d e f
0 0 1
0 0 0
1 1 0
1 0 0
1 0
1
1 0 1
0 1 0 0 0 1
1
2
3
4
g h
0
1
0
0
1
1
1
1
Edges
Paths
5 1
0 0 0
0 1 1
0 1 1 1 1 0
6
0
1
1

10.  A graph, G, consist of two sets, V and E.
 E is set of pairs of vertices called edges. V is a finite, nonempty
set of vertices.
 The vertices of a graph G can be represented as V(G).
 Likewise, the edges of a graph, G, can be represented
as E(G).
 Graphs can be either undirected graphs or directed
graphs.
 For a undirected graph, a pair of vertices (u, v) or (v, u)
represent the same edge.
 For a directed graph, a directed pair <u, v> has u as the
tail and the v as the head. Therefore, <u, v> and <v, u>
represent different edges.

11.  (c) G3) = {0,
0
1 2
3
0
1
3 4
2
5 6
1
2
V(G2) = {0, 1, 2, 3, 4, 5, 6}
E(G2) = {(0, 1), (0, 2), (1, 3), (1, 4),
(2, 5), (2, 6)}
V(G1) = {0, 1, 2, 3}
E(G1) = {(0, 1), (0, 2), (0, 3), (1, 2),
(1, 3), (2, 3)}
(a) G1
(c) G3
V(G3 1, 2}
E(G3) = {<0, 1>, <1, 0>, <1, 2>}

12.  There are several roughly equivalent definitions
of a graph. Most commonly, a graph G is
defined as an ordered pair G=(V,E) ,
where V={v1 ,v2,….} is called the
graph's vertex-set and E= {e1,e2,…} is called
the graph's edge-set.

13.  A graph may not have an edge from a vertex
back to itself.
 (v, v) or <v, v> are called self edge or self loop. If a
graph with self edges, it is called a graph with self
edges.
v1 A graph man not have multiple occurrences of
the same edge.
 If without this restriction, it is called a multigraph.

14. 0
2
1 1
 (a) Graph with a self edge
2
3
(b) Multigraph

15.  Degree of a vertex: The degree of a vertex is the
number of edges incident to that vertex.
 If G is a directed graph, then we define
 in-degree of a vertex: is the number of edges
for which vertex is the head.
 out-degree of a vertex: is the number of edges
for which the vertex is the tail.

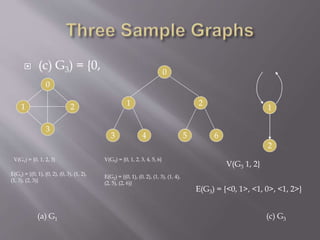
16.  Let G(V, E) be a graph with n vertices, n ≥ 1. The
adjacency matrix of G is a two-dimensional nxn array,
A.
 A[i][j] = 1 iff the edge (i, j) is in E(G).
 The adjacency matrix for a undirected graph is symmetric, it
may not be the case for a directed graph.
 For an undirected graph the degree of any vertex i is its
row sum.
 For a directed graph, the row sum is the out-degree
and the column sum is the in-degree.

17.  Planar graphs are graphs that may be drawn
on a 2-dimensional plane without having any
of the edges intersect. Below are several planar
graphs that are also complete graphs.
