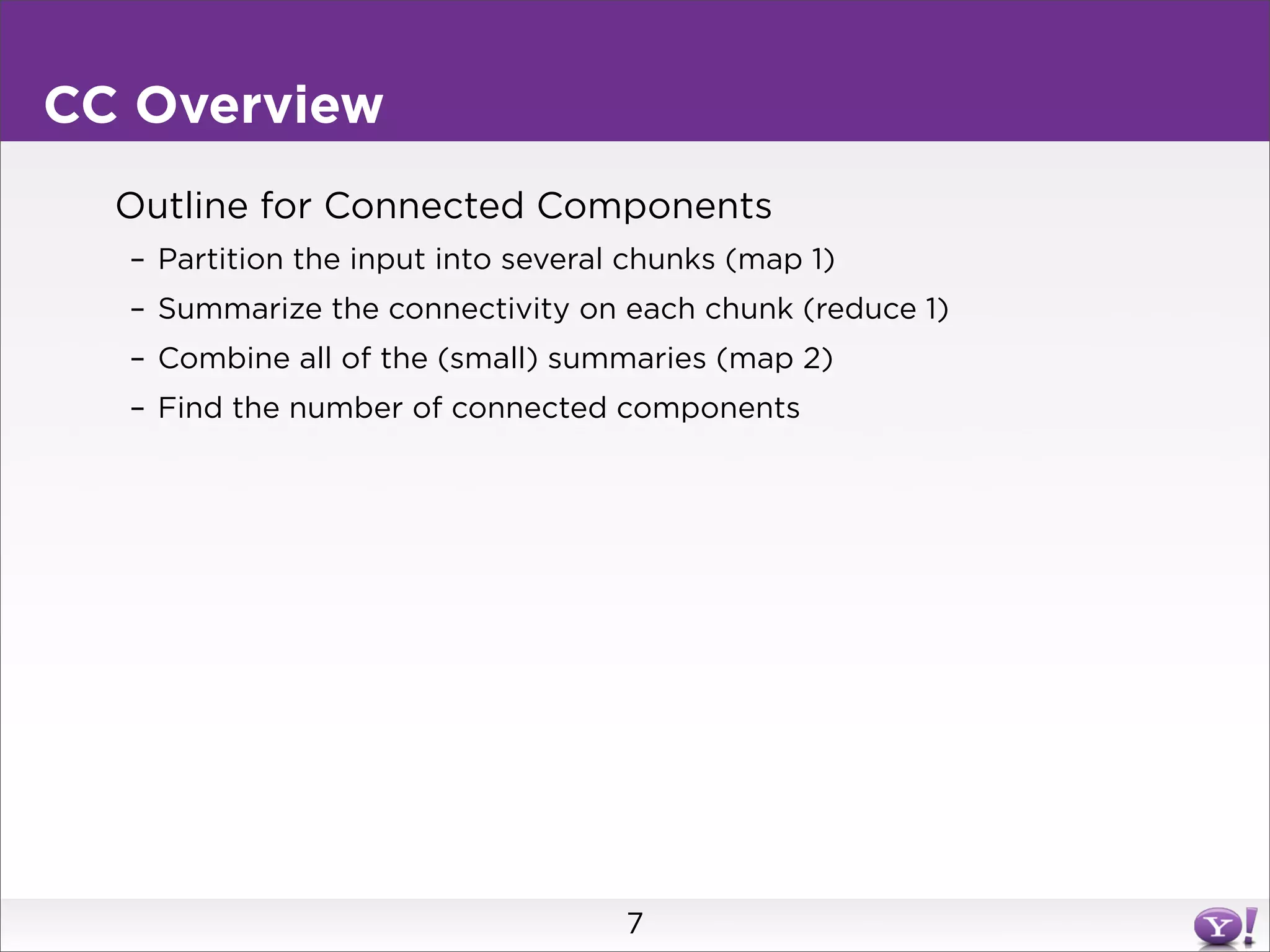
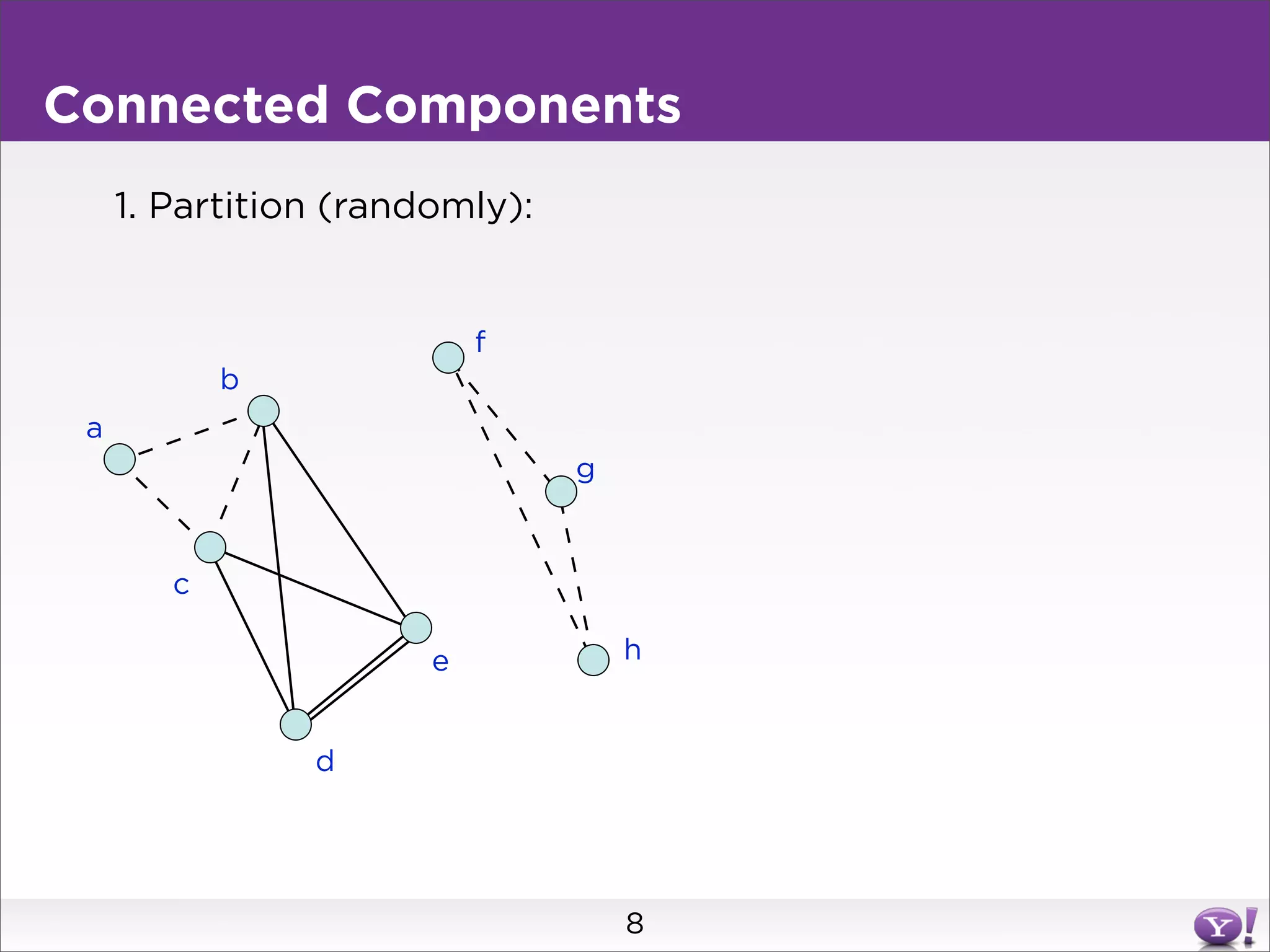
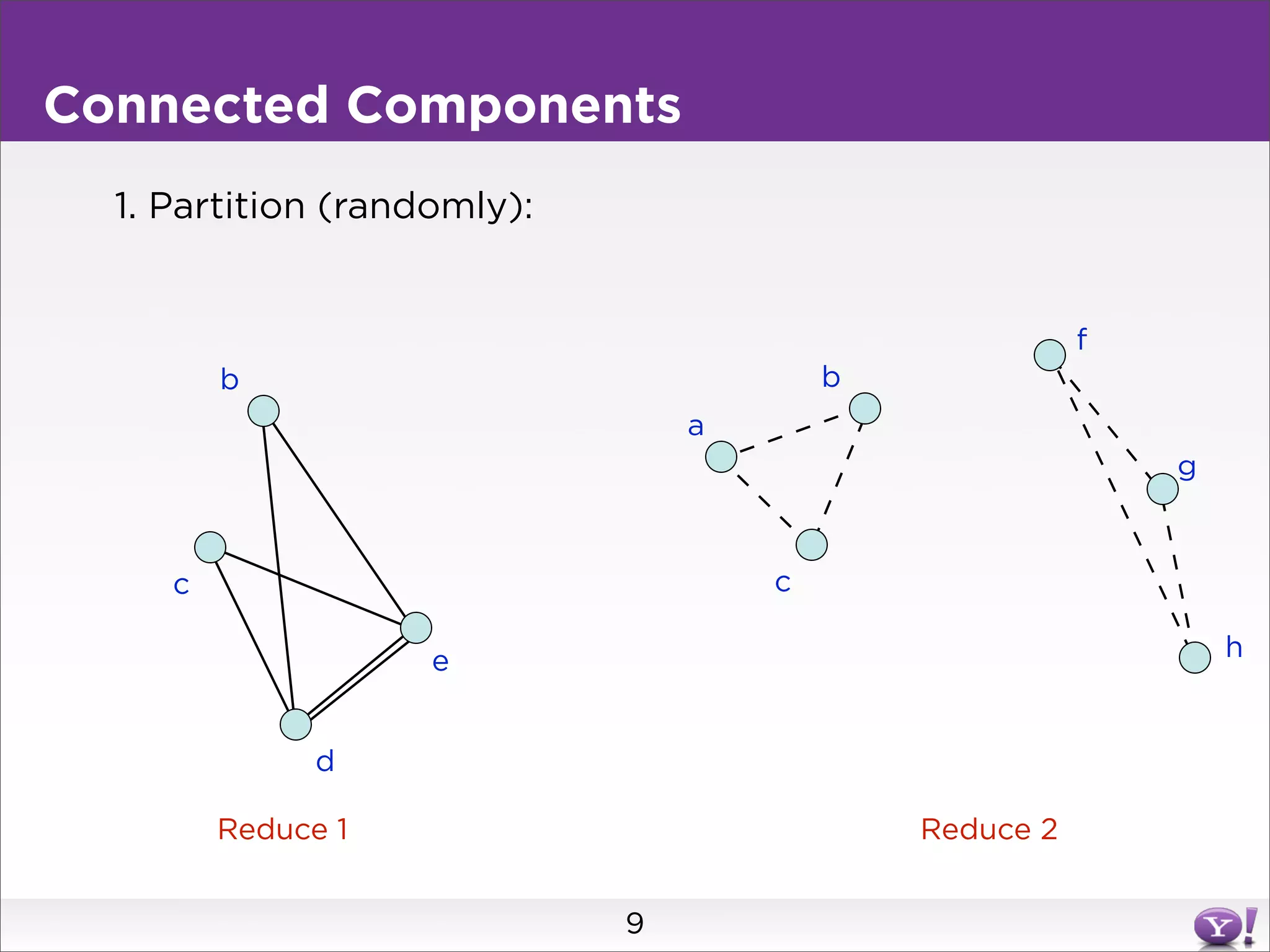
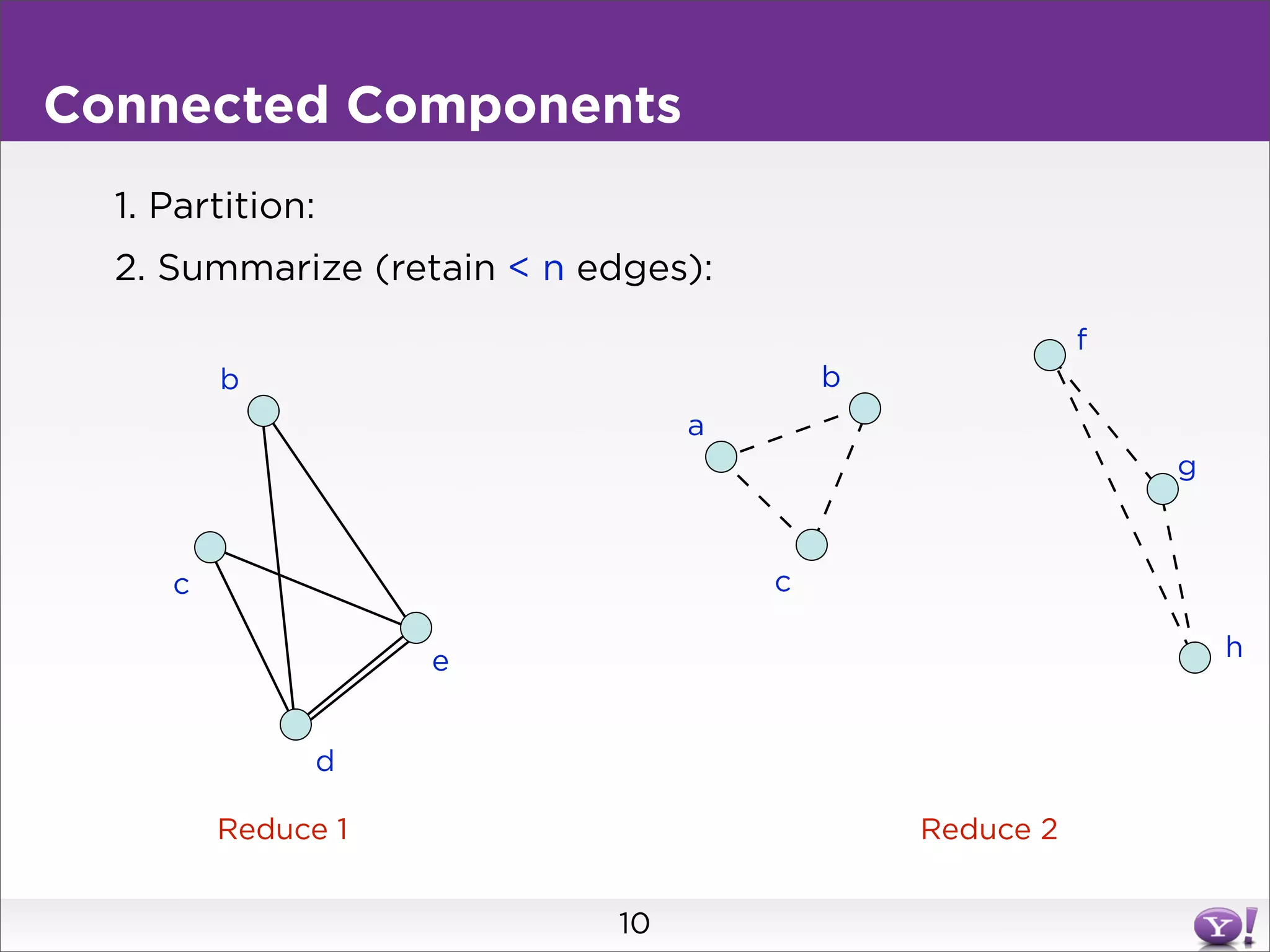
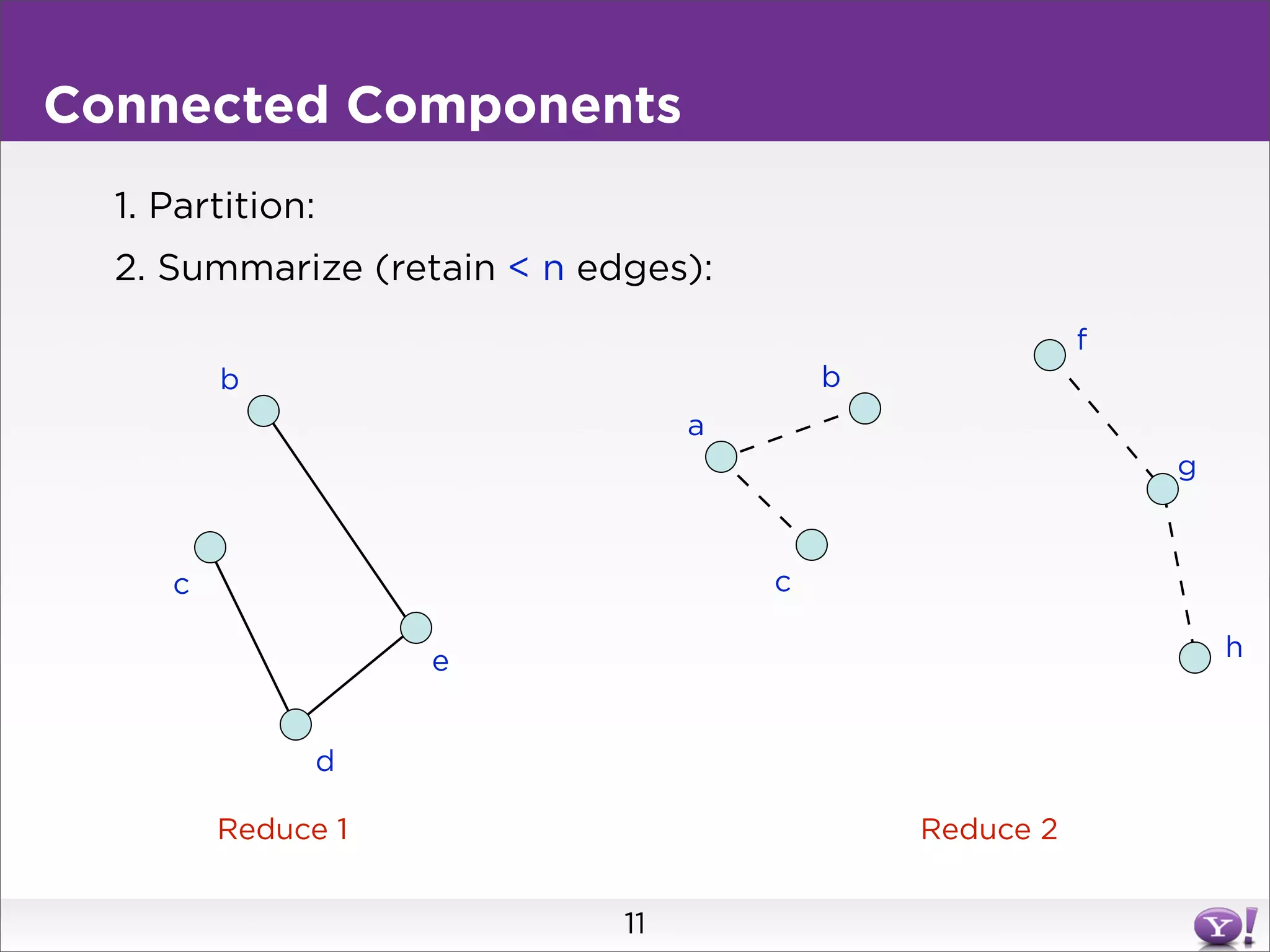
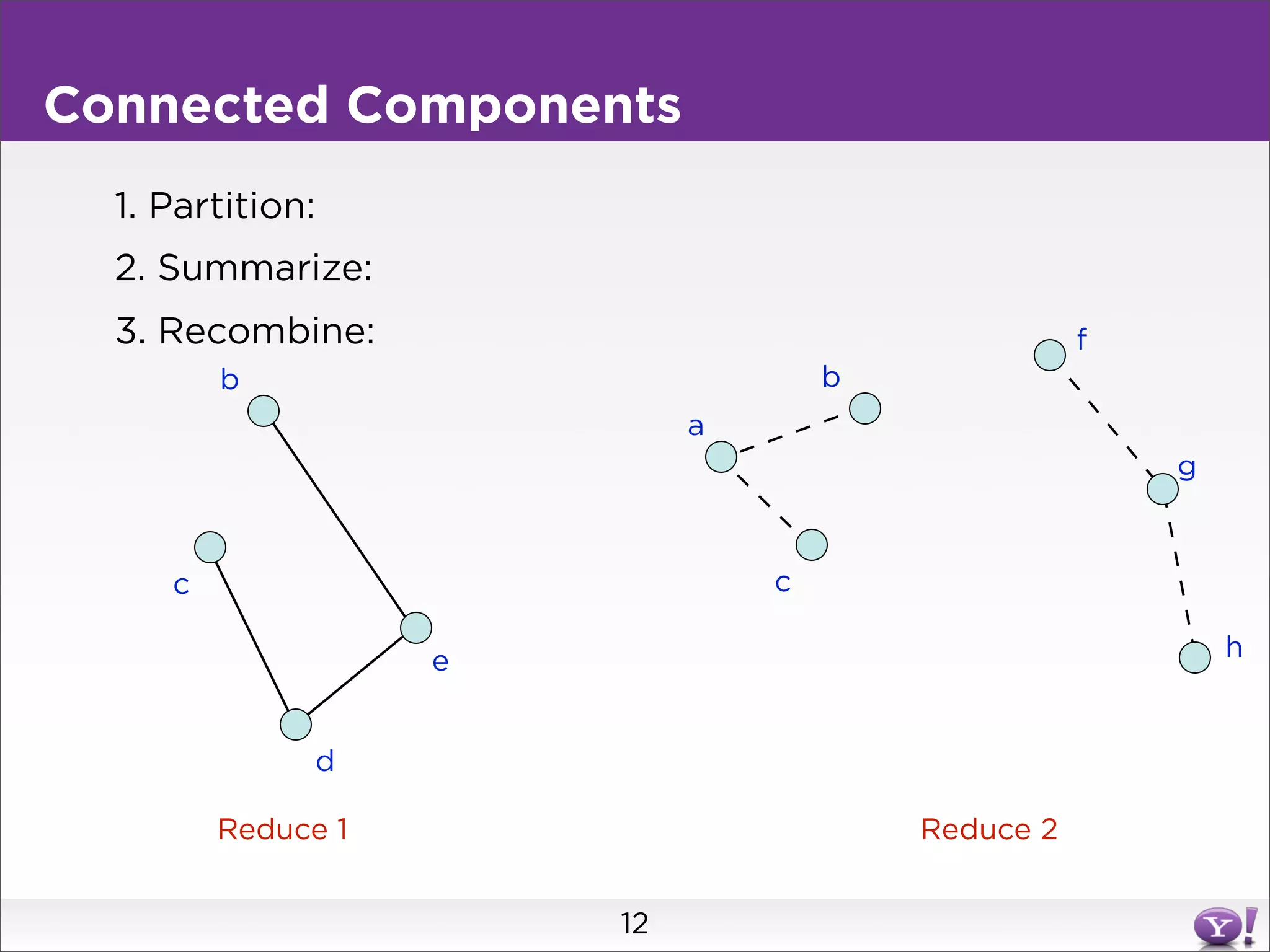
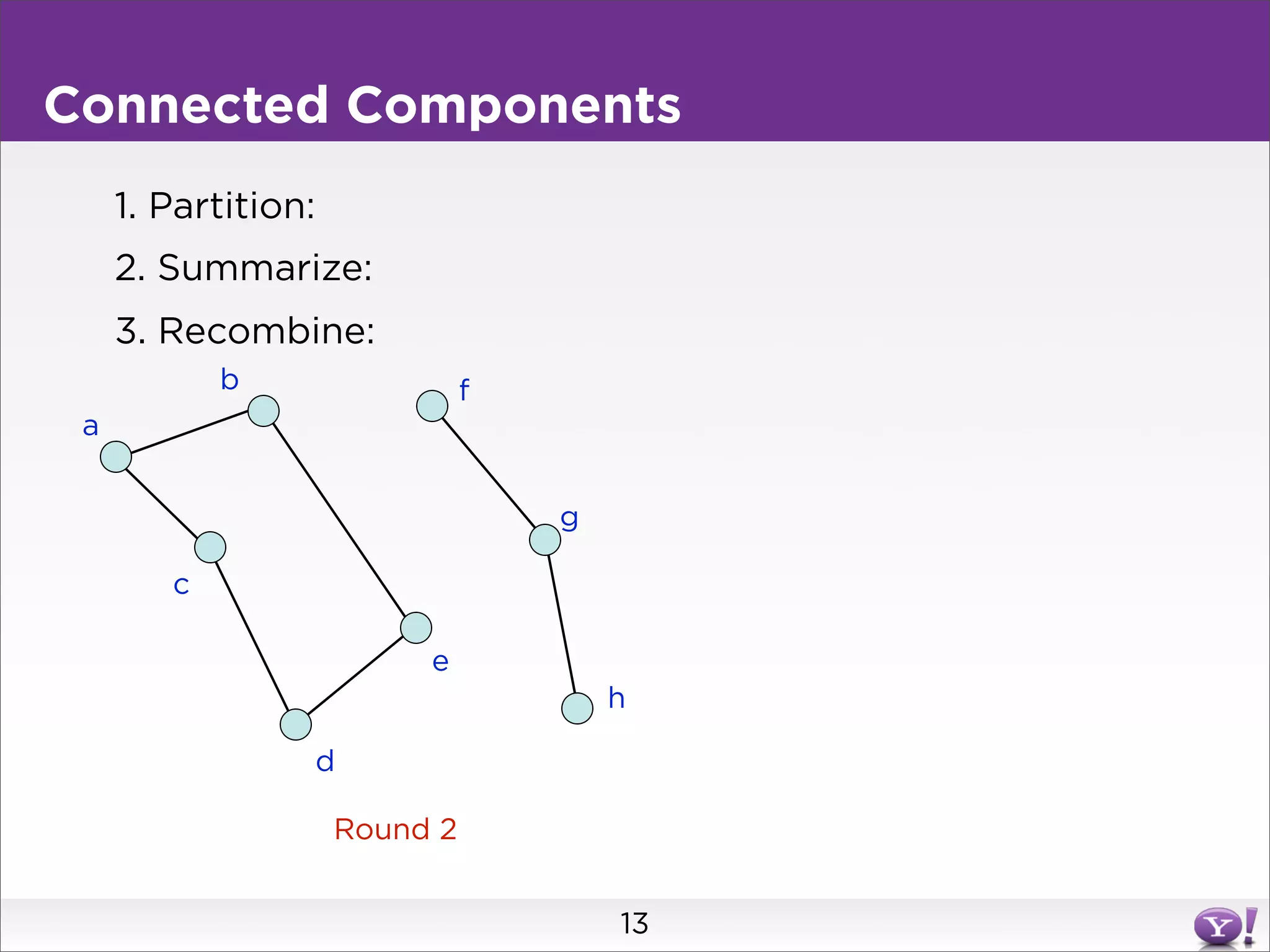
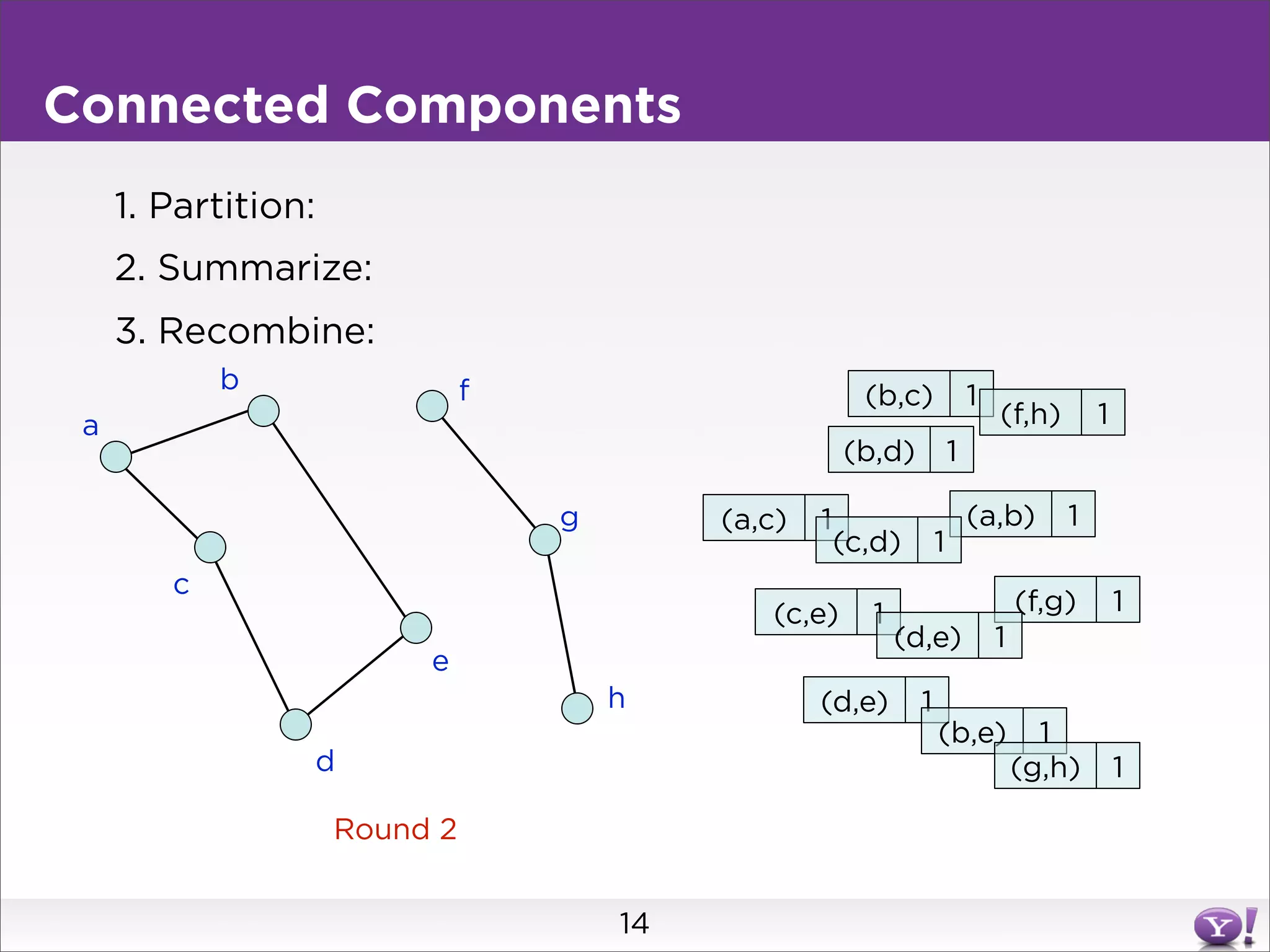
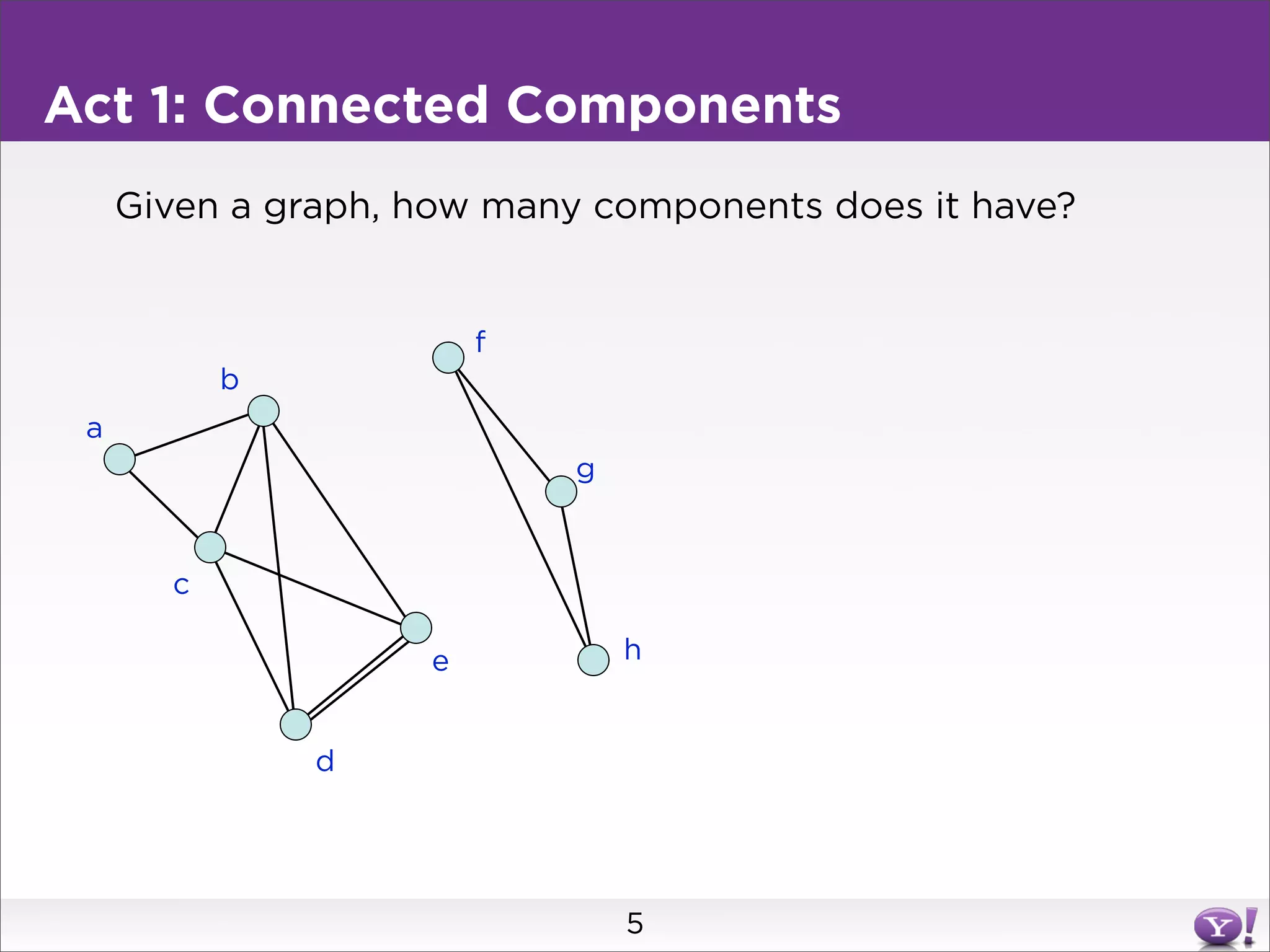
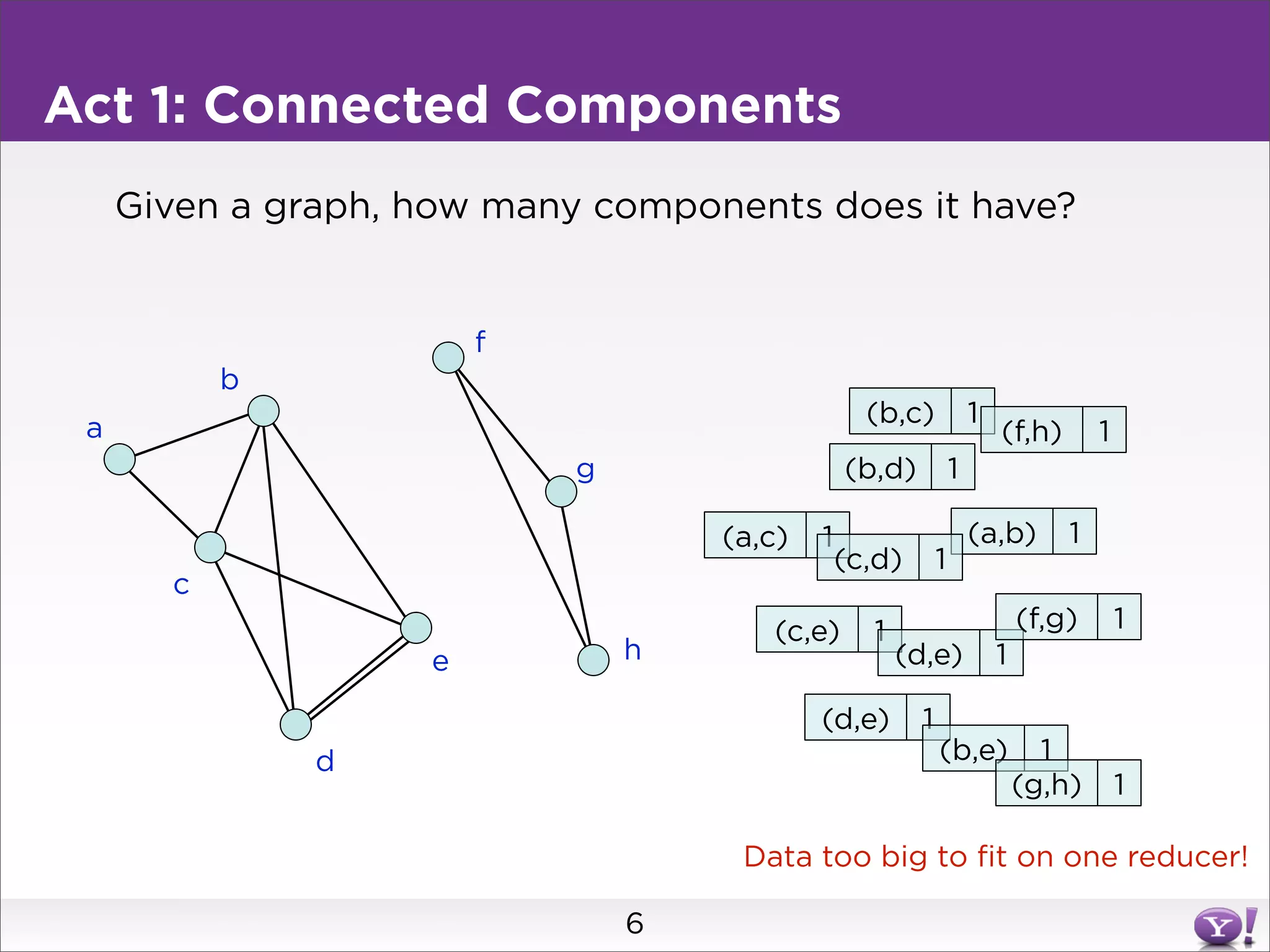
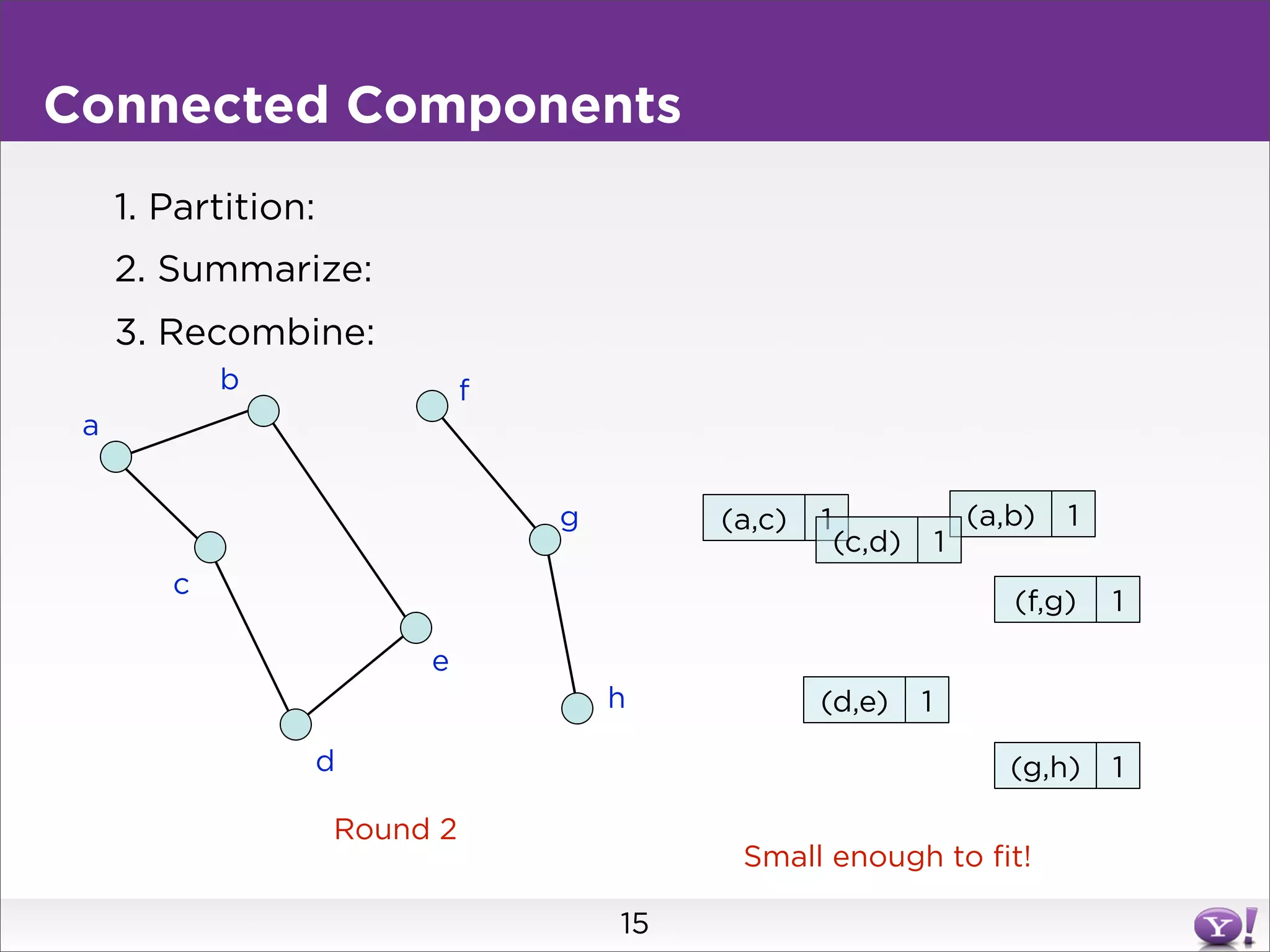
This document summarizes two graph algorithms for analyzing large graphs: connected components and clustering coefficient. For connected components, it describes a two step approach: 1) partition the graph and summarize connectivity on each partition, reducing data size, and 2) recombine the summaries to find the overall connected components. This approach works for other problems like finding minimum spanning trees by summarizing each partition. 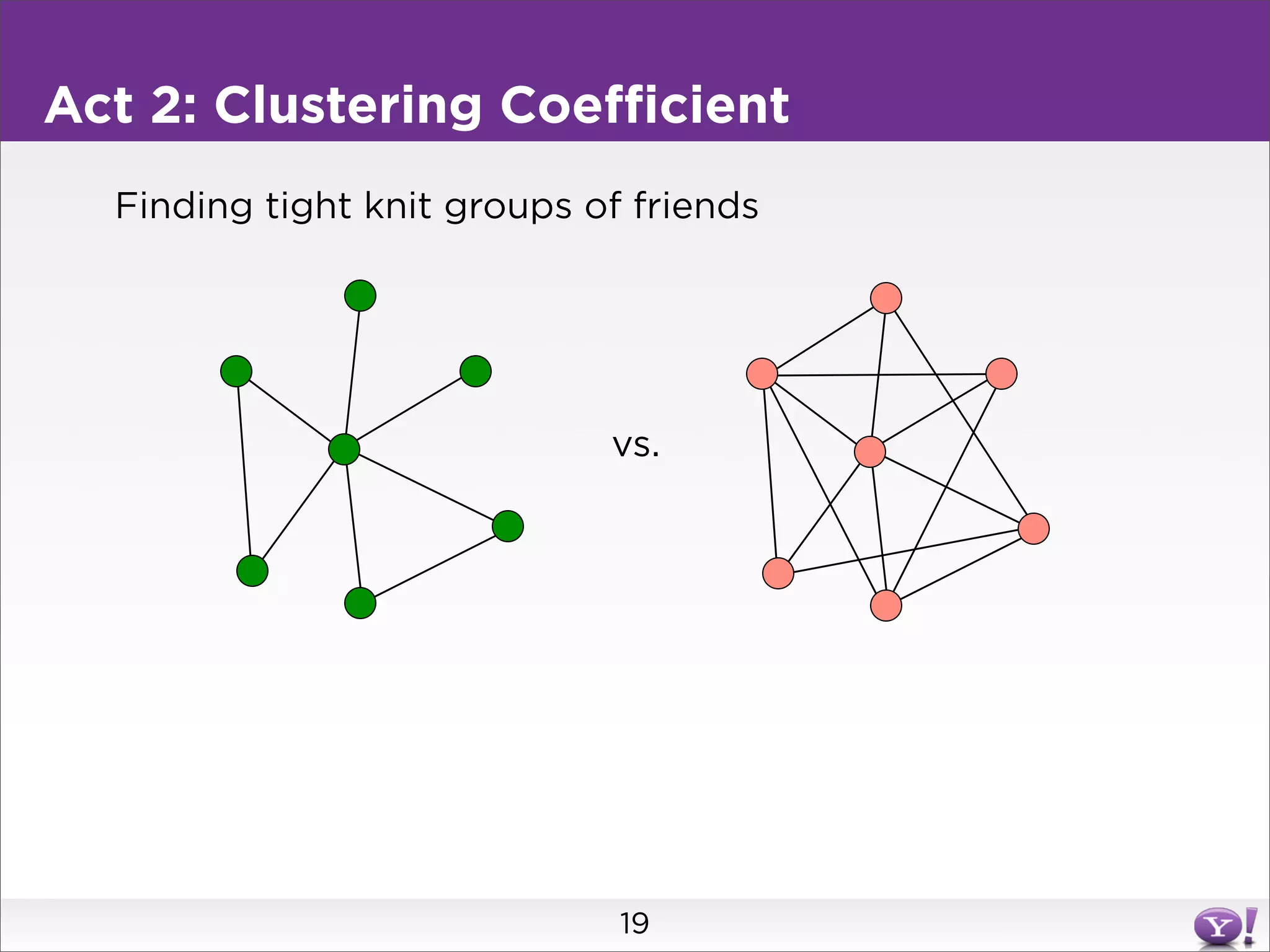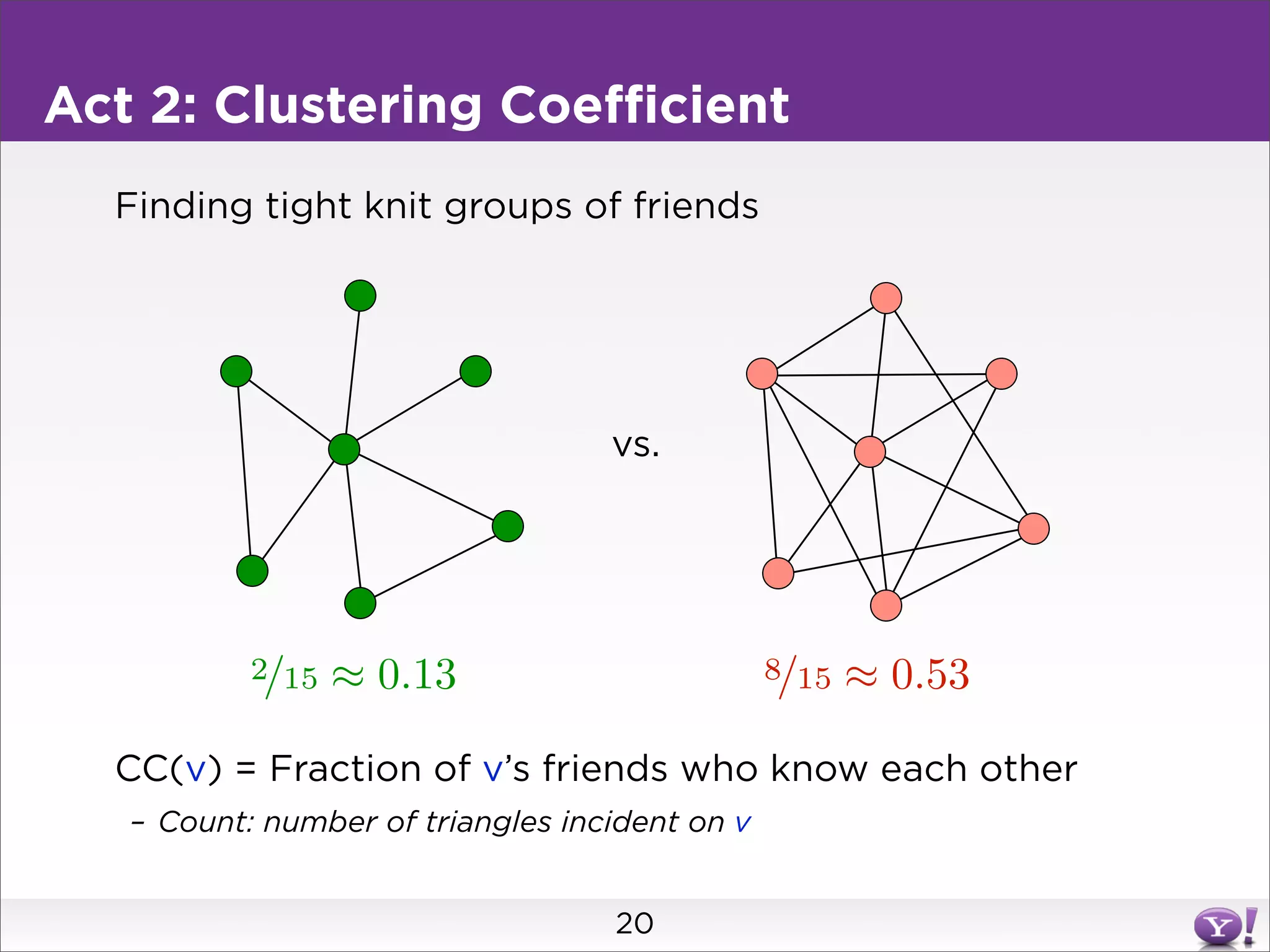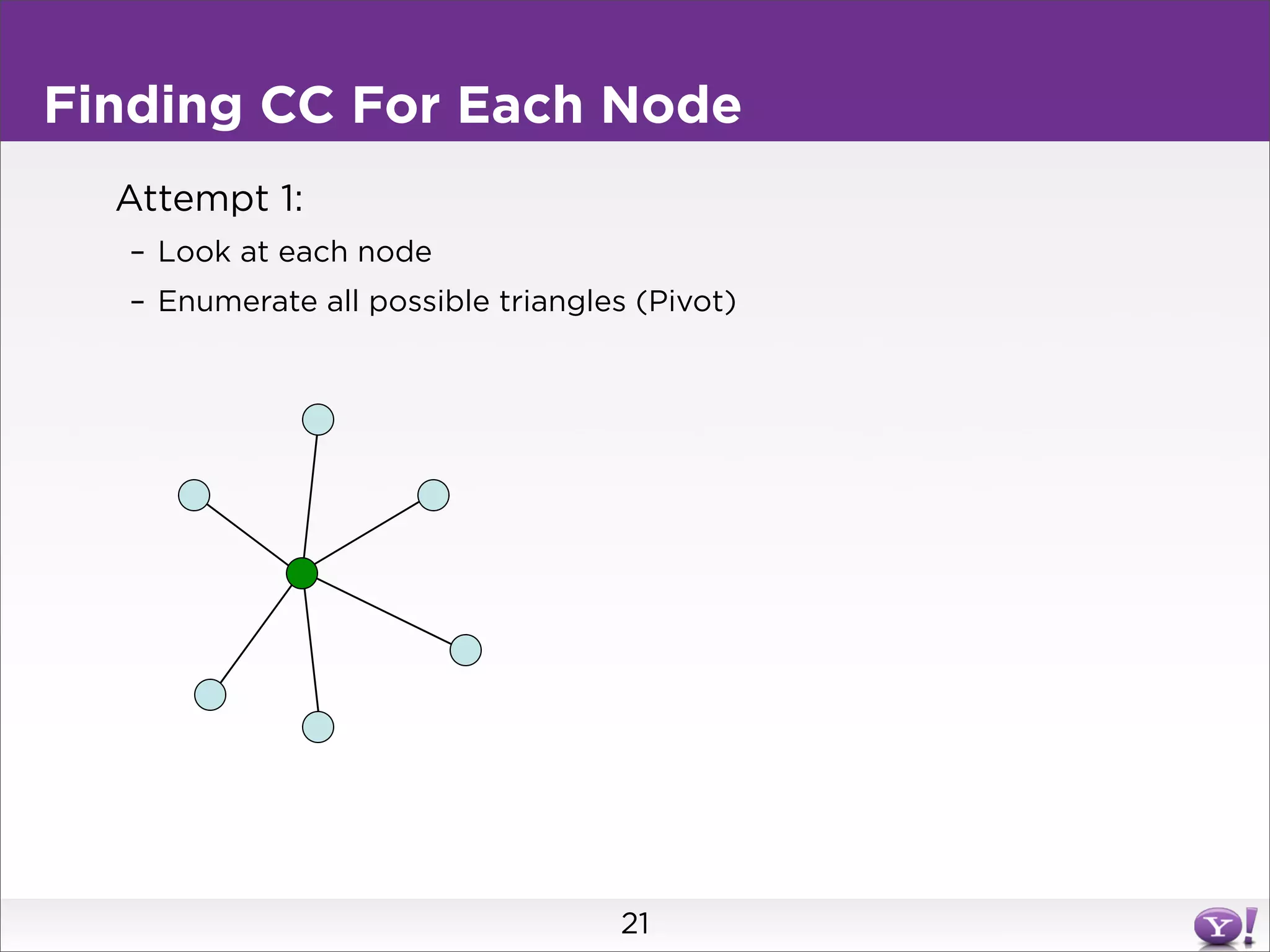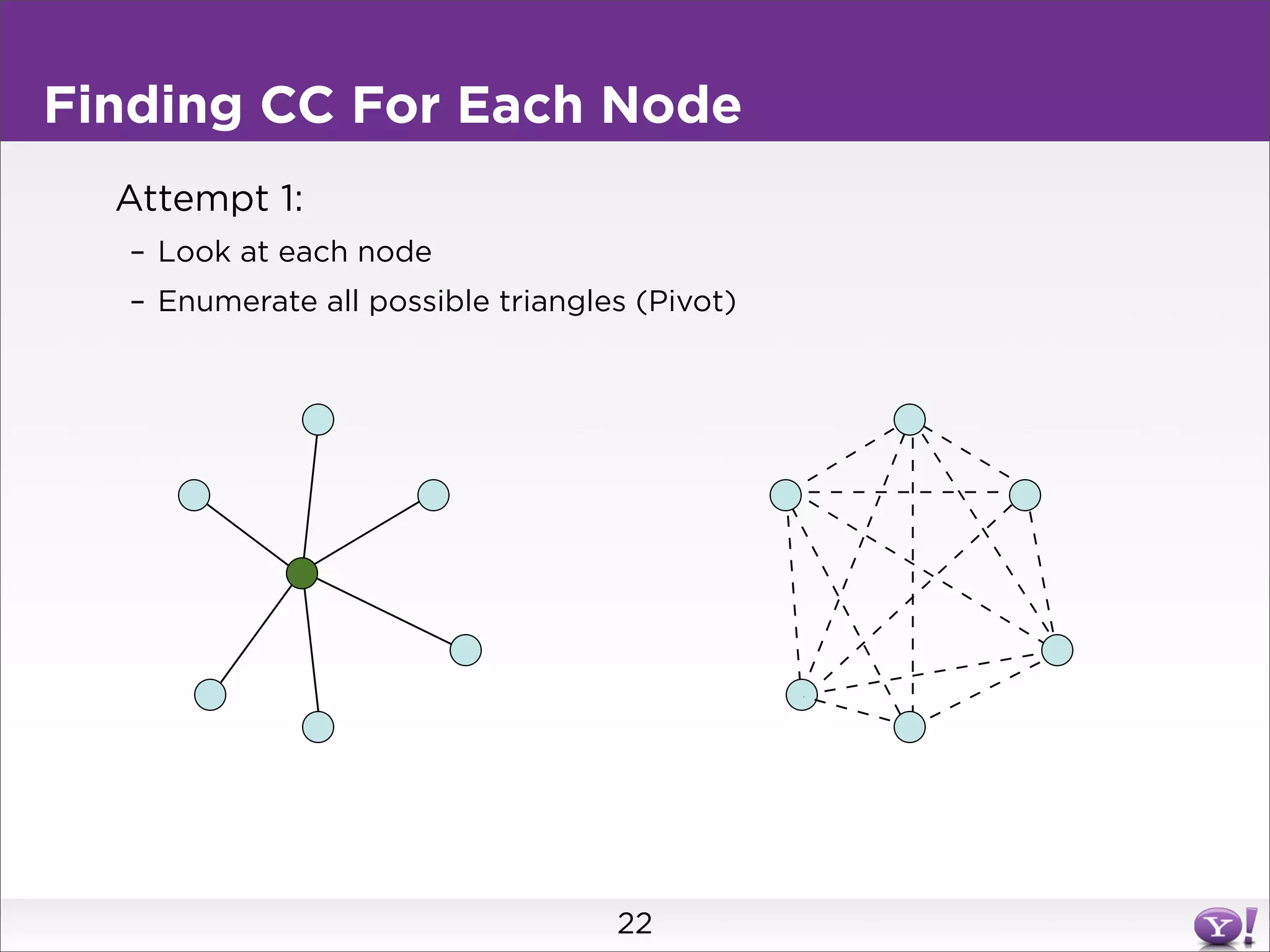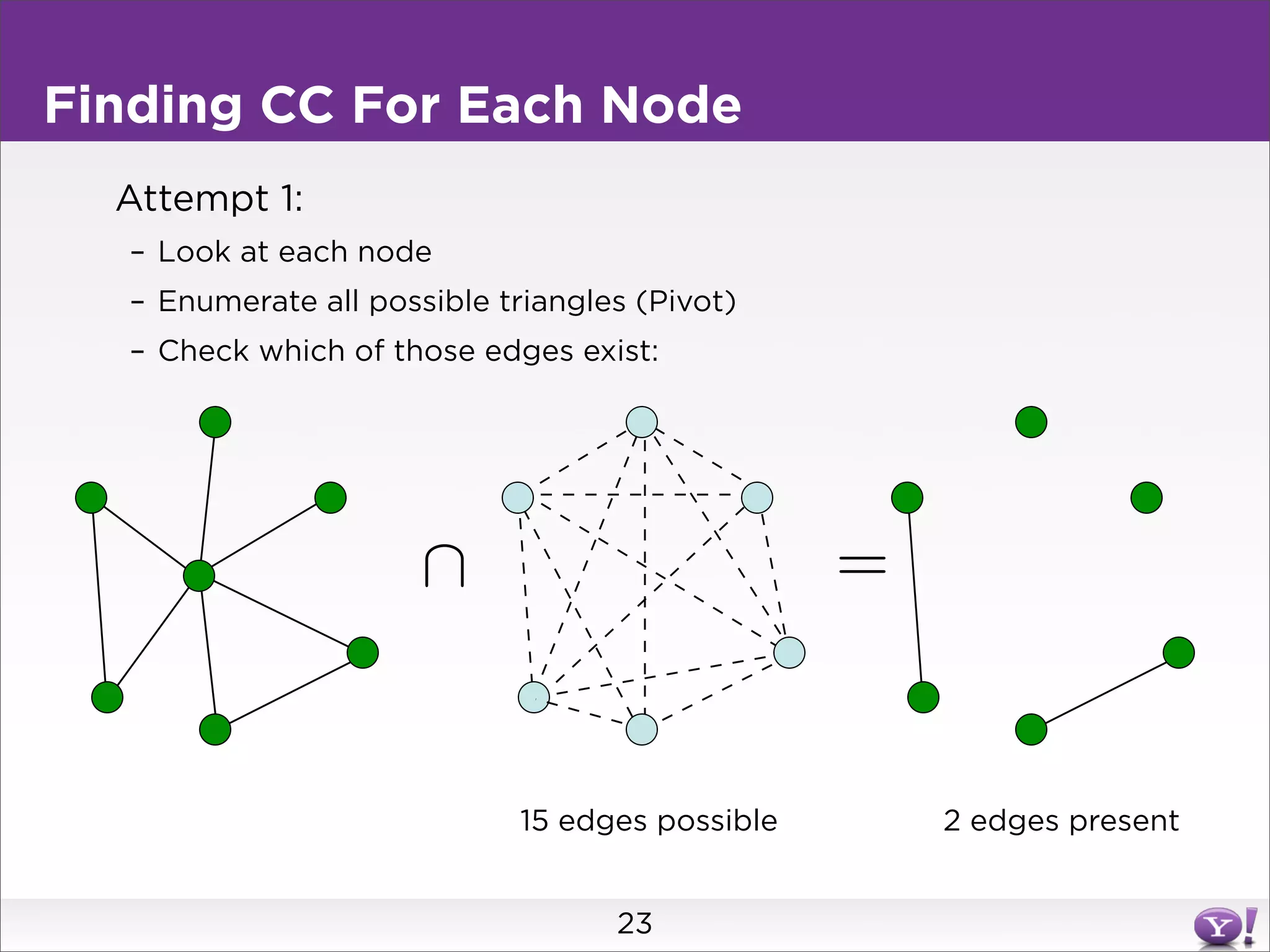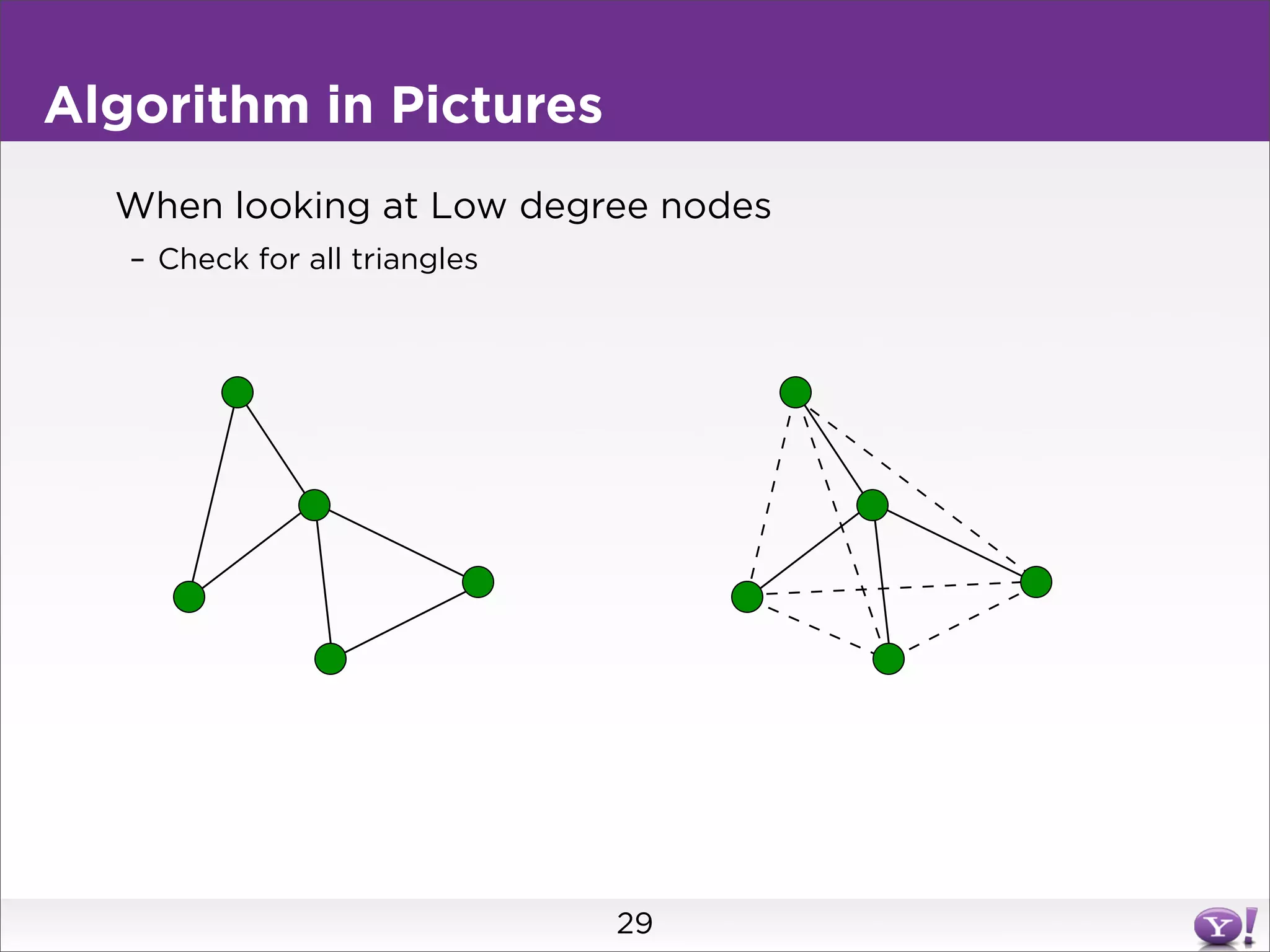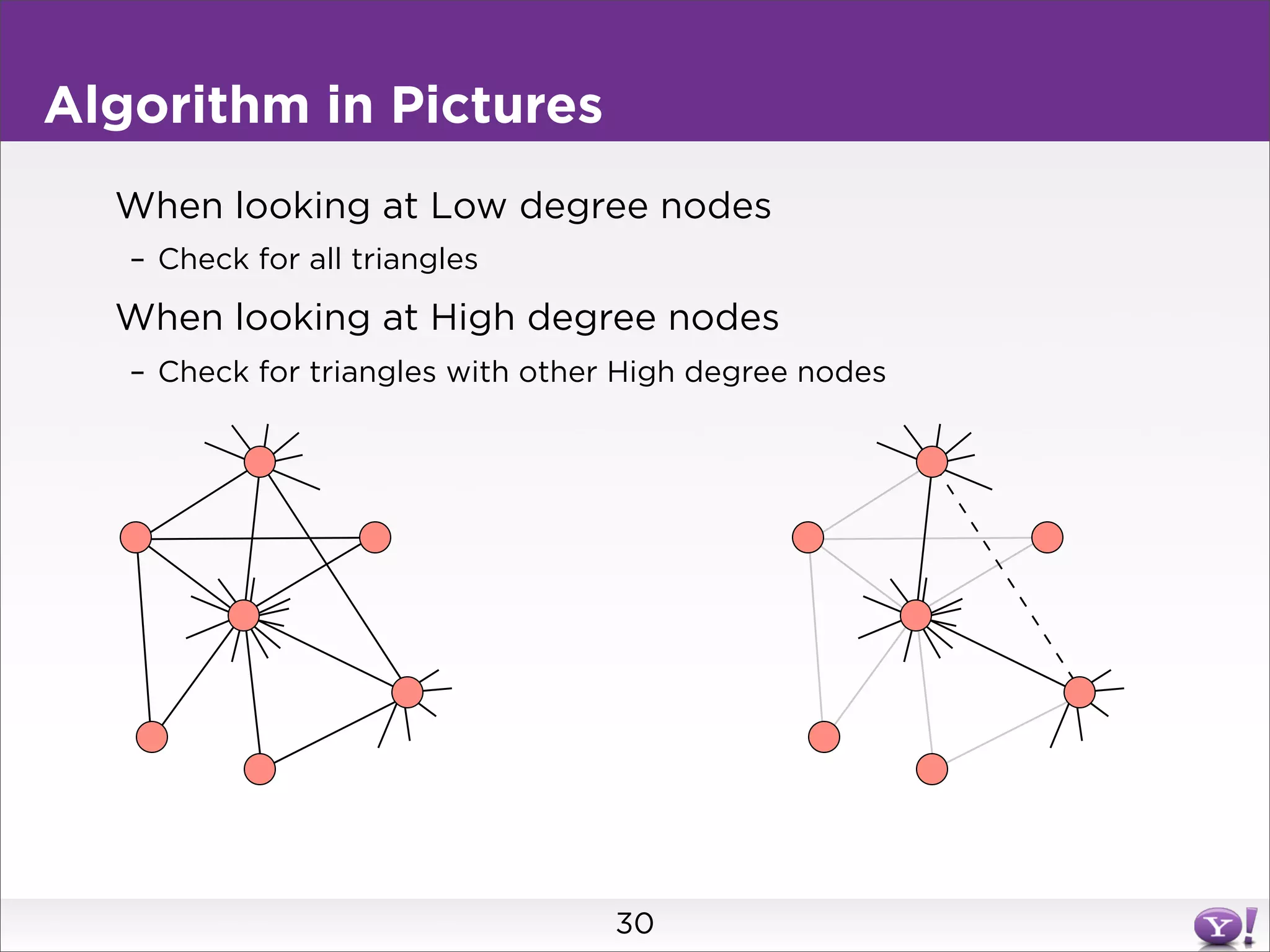For clustering coefficient, it describes the challenge of enumerating all possible triangles for each node, which generates quadratic intermediate data. A different approach is needed to scale to very high degree nodes with millions of connections.

1. XXL Graph Algorithms
Sergei Vassilvitskii
Yahoo! Research
With help from Jake Hofman, Siddharth Suri, Cong Yu and many others

2. Introduction
XXL Graphs are everywhere:
– Web graph
– Friend graphs
– Advertising graphs...
2

3. Introduction
XXL Graphs are everywhere:
– Web graph
– Friend graphs
– Advertising graphs...
But we have Hadoop!
– Few algorithms have been ported (no Hadoop Algorithms book)
– Few general algorithmic approaches
– Active area of research
3

4. Outline
Today:
– Act 1: Crawl before you walk
• Counting connected components
– Act 2: The curse of the last reducer
• Finding tight knit friend groups
4

5. Act 1: Connected Components
Given a graph, how many components does it have?
f
b
a
g
c
e h
d
5

6. Act 1: Connected Components
Given a graph, how many components does it have?
f
b
(b,c) 1
a (f,h) 1
g (b,d) 1
(a,c) 1 (a,b) 1
(c,d) 1
c
(c,e) 1 (f,g) 1
e h (d,e) 1
(d,e) 1
d (b,e) 1
(g,h) 1
Data too big to fit on one reducer!
6

7. CC Overview
Outline for Connected Components
– Partition the input into several chunks (map 1)
– Summarize the connectivity on each chunk (reduce 1)
– Combine all of the (small) summaries (map 2)
– Find the number of connected components
7

8. Connected Components
1. Partition (randomly):
f
b
a
g
c
e h
d
8

9. Connected Components
1. Partition (randomly):
f
b b
a
g
c c
e h
d
Reduce 1 Reduce 2
9

10. Connected Components
1. Partition:
2. Summarize (retain < n edges):
f
b b
a
g
c c
e h
d
Reduce 1 Reduce 2
10

11. Connected Components
1. Partition:
2. Summarize (retain < n edges):
f
b b
a
g
c c
e h
d
Reduce 1 Reduce 2
11

12. Connected Components
1. Partition:
2. Summarize:
3. Recombine: f
b b
a
g
c c
e h
d
Reduce 1 Reduce 2
12

13. Connected Components
1. Partition:
2. Summarize:
3. Recombine:
b f
a
g
c
e
h
d
Round 2
13

14. Connected Components
1. Partition:
2. Summarize:
3. Recombine:
b f (b,c) 1
a (f,h) 1
(b,d) 1
g (a,c) 1 (a,b) 1
(c,d) 1
c
(c,e) 1 (f,g) 1
(d,e) 1
e
h (d,e) 1
(b,e) 1
d (g,h) 1
Round 2
14

15. Connected Components
1. Partition:
2. Summarize:
3. Recombine:
b f
a
g (a,c) 1 (a,b) 1
(c,d) 1
c
(f,g) 1
e
h (d,e) 1
d (g,h) 1
Round 2
Small enough to fit!
15

16. Connected Components
The summarization does not affect connectivity
– Drops redundant edges
– Dramatically reduces data size
– Takes two MapReduce rounds
16

17. Connected Components
The summarization does not affect connectivity
– Drops redundant edges
– Dramatically reduces data size
– Takes two MapReduce rounds
Similar approach works in other situations:
– Consider vertices connected only if k edges between vertices
– Consider vertices connected if similarity score above a threshold
• E.g. approximate Jaccard similarity when computing for recommendation
systems
– Find minimum spanning trees
• Summarize by computing an MST on the subset graph
– Clustering
• Cluster each partition, then aggregate the clusters
17

18. Outline
Today:
– Act 1: Crawl before you walk
• Counting connected components
– Act 2: The curse of the last reducer
• Finding tight knit friend groups
18

19. Act 2: Clustering Coefficient
Finding tight knit groups of friends
19

20. Act 2: Clustering Coefficient
Finding tight knit groups of friends
vs.
19

21. Act 2: Clustering Coefficient
Finding tight knit groups of friends
vs.
2/15 ≈ 0.13 8/15 ≈ 0.53
CC(v) = Fraction of v’s friends who know each other
– Count: number of triangles incident on v
20

22. Finding CC For Each Node
Attempt 1:
– Look at each node
– Enumerate all possible triangles (Pivot)
21

23. Finding CC For Each Node
Attempt 1:
– Look at each node
– Enumerate all possible triangles (Pivot)
22

24. Finding CC For Each Node
Attempt 1:
– Look at each node
– Enumerate all possible triangles (Pivot)
– Check which of those edges exist:
∩ =
15 edges possible 2 edges present
23

25. Finding CC For Each Node
Attempt 1:
– Look at each node
– Enumerate all possible triangles (Pivot)
– Check which of those edges exist
24

26. Finding CC For Each Node
Attempt 1:
– Look at each node
– Enumerate all possible triangles
– Check which of those edges exist
Amount of intermediate data
– Quadratic in the degree of the nodes
– 6 friends: 15 possible triangles
– n friends, n(n-1)/2 possible triangles
25

27. Finding CC For Each Node
Attempt 1:
– Look at each node
– Enumerate all possible triangles
– Check which of those edges exist
Amount of intermediate data
– Quadratic in the degree of the nodes
– 6 friends: 15 possible triangles
– n friends, n(n-1)/2 possible triangles
There’s always “that guy”:
– tens of thousands of friends
– tens of thousands of movie ratings (really!)
– millions of followers
26

28. Finding CC For Each Node
Attempt 1:
– Look at each node a le
Sc triangles
ot
– Enumerate all possible
sn
oe
– Check which of those edges exist
D
27

29. Finding CC For Each Node
Attempt 1:
– Look at each node a le
Sc triangles
ot
– Enumerate all possible
sn
oe
– Check which of those edges exist
D
Attempt 2:
– There is a limited number of High degree nodes
– Count LLL, LLH, LHH, and HHH triangles differently
– If a triangle has at least one Low node
– Pivot on Low node to count the triangles
– If a triangle has all High nodes
– Pivot but only on other neighboring High nodes (not all nodes)
28

30. Algorithm in Pictures
When looking at Low degree nodes
– Check for all triangles
29

31. Algorithm in Pictures
When looking at Low degree nodes
– Check for all triangles
When looking at High degree nodes
– Check for triangles with other High degree nodes
30

32. Clustering Coefficient Discussion
Attempt 2:
– Main idea: treat High and Low degree nodes differently
• Limit the amount of data generated (No more than O(n) per node)
– All triangles accounted for
– Can set High-Low threshold to balance the two cases
• Rule of thumb: threshold around square root of number of vertices
– A bit more complex, but still easy to code
• Doesn’t suffer from the one high degree node problem
31

33. XXL Graphs: Conclusions
Algorithm Design
– Prove performance guarantees independent of input data
• Input skew (e.g. high degree nodes) should not severely affect
algorithm performance
• Number of rounds fixed (and hopefully small)
32

34. XXL Graphs: Conclusions
Algorithm Design
– Prove performance guarantees independent of input data
• Input skew (e.g. high degree nodes) should not severely affect
algorithm performance
• Number of rounds fixed (and hopefully small)
Rethink graph algorithms:
– Connected Components: Two round approach
– Clustering Coefficient: High-Low node decomposition
– (Breaking News) Matchings: Two round sampling technique
33

35. Thank You
sergei@yahoo-inc.com