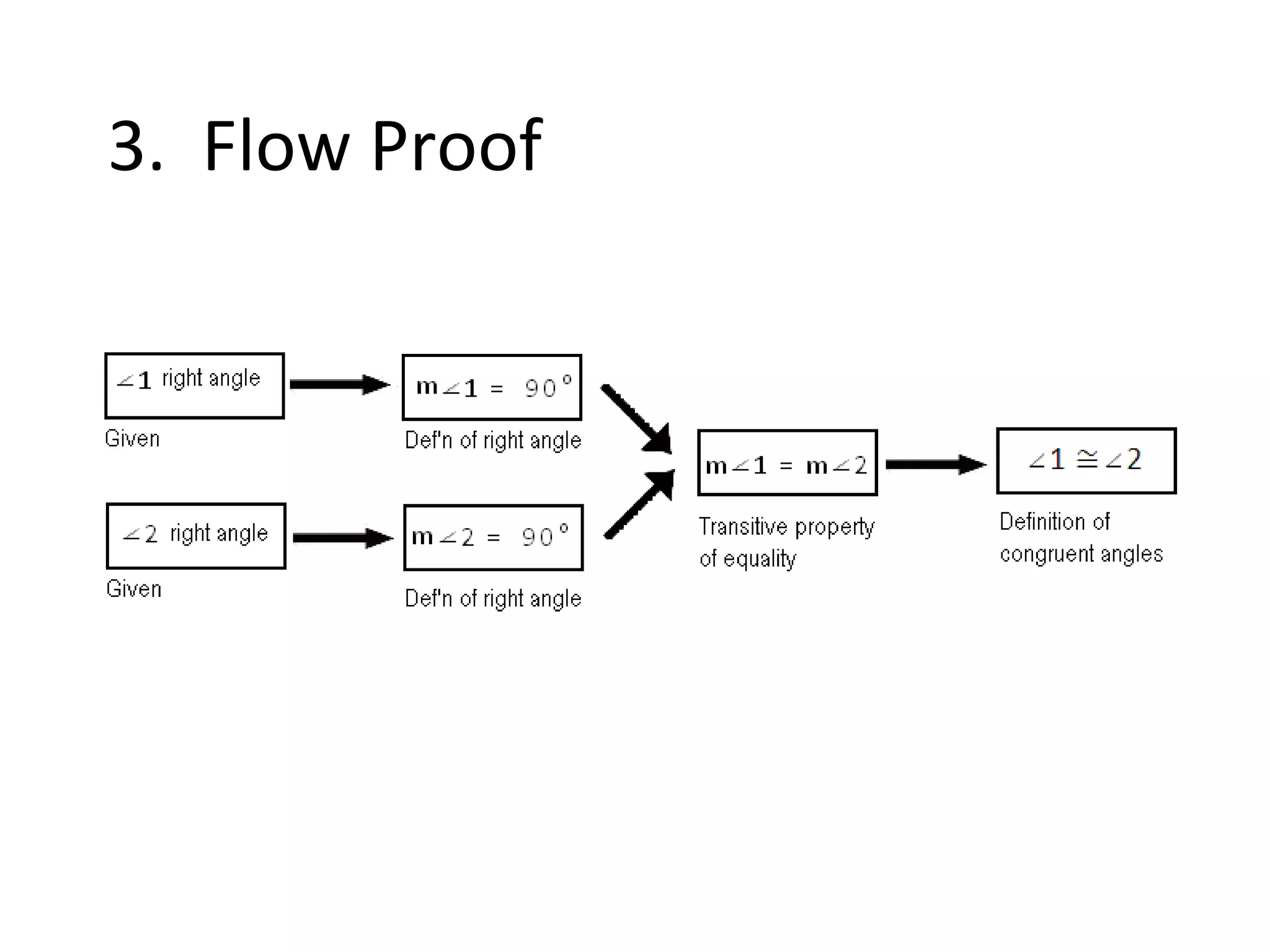
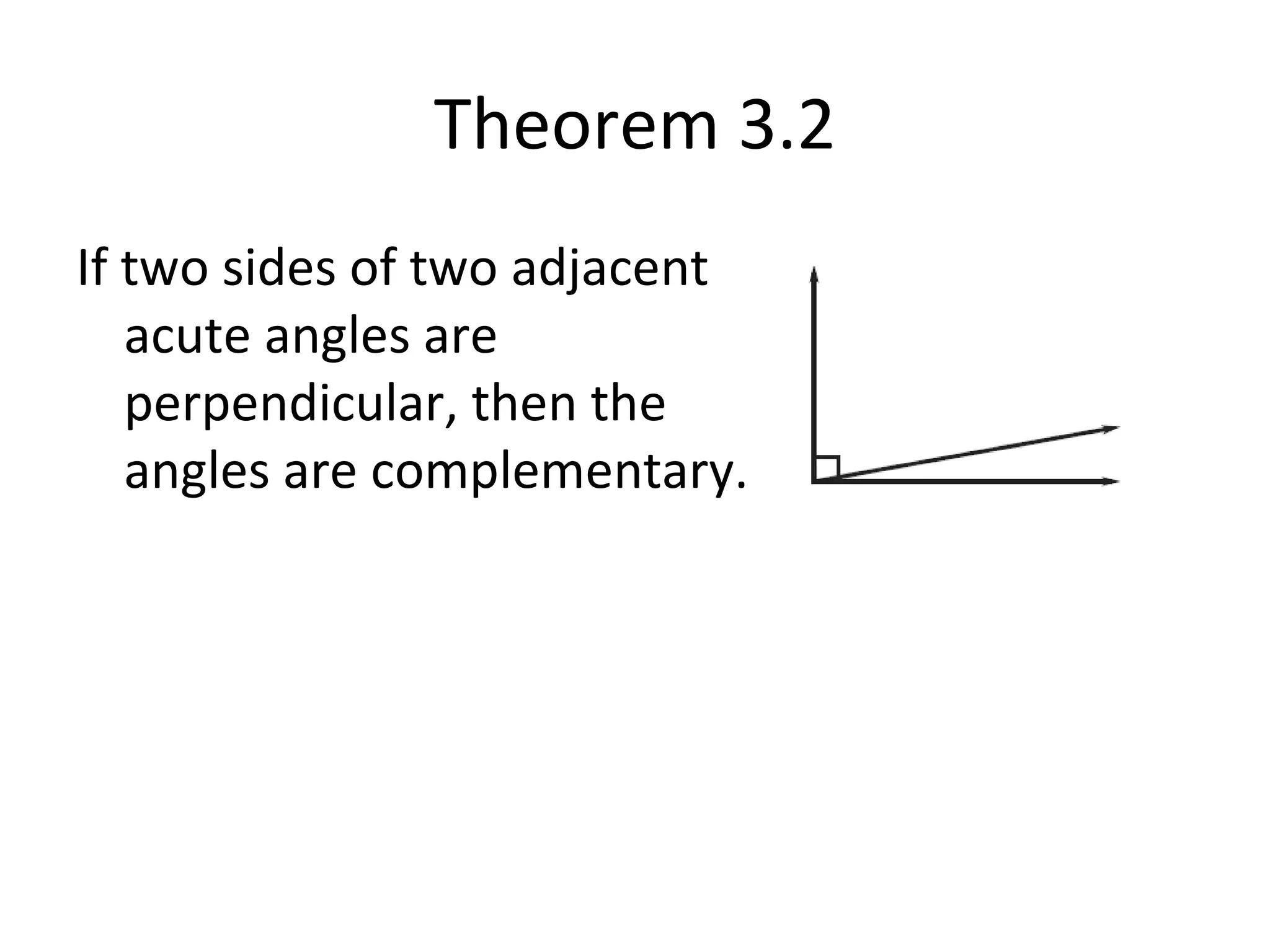
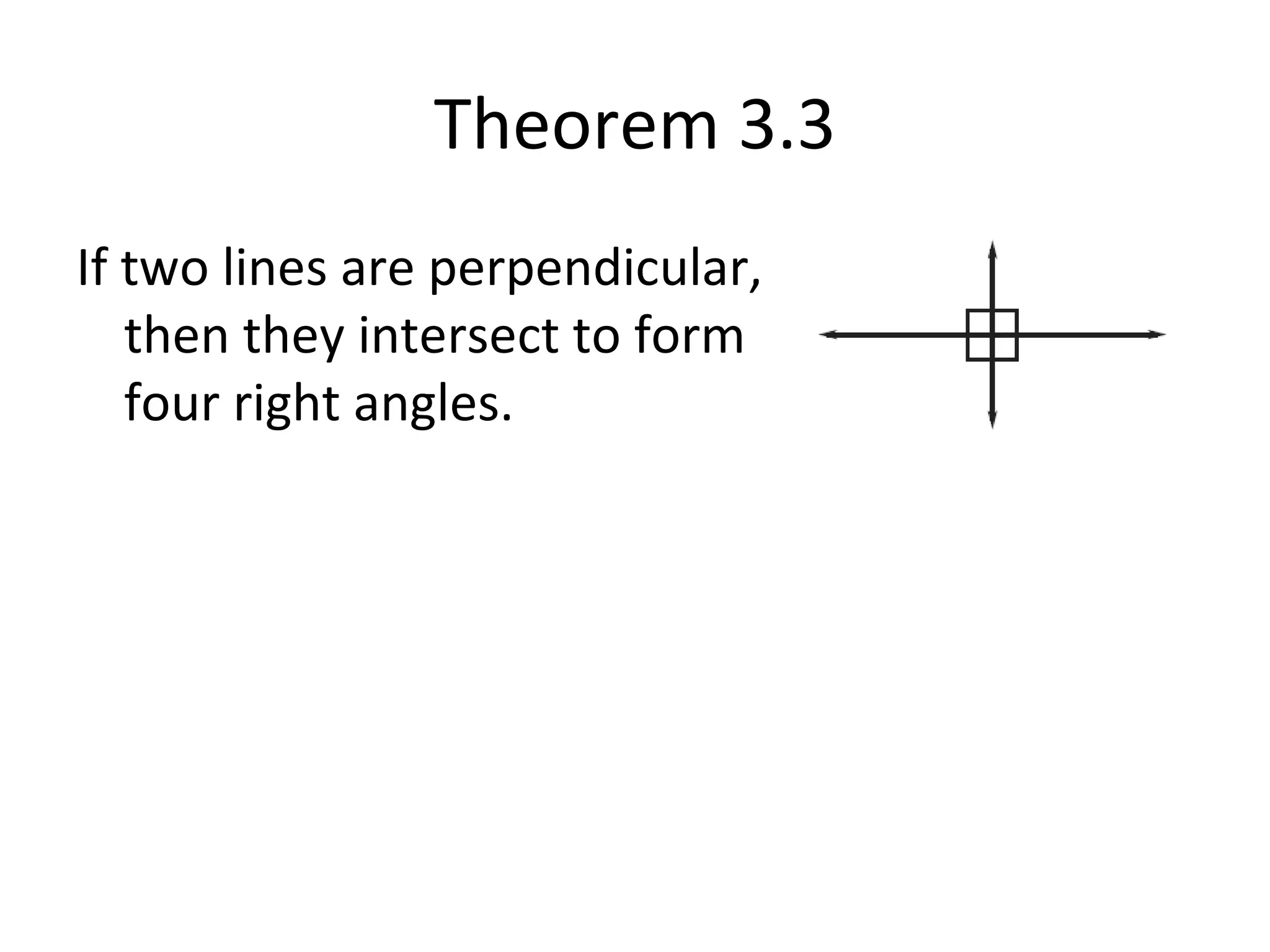
The document discusses different types of proofs used to prove theorems about perpendicular lines. It presents three theorems: 1) if two lines intersect to form congruent angles, they are perpendicular, 2) if two adjacent acute angles have perpendicular sides, they are complementary, and 3) if two lines are perpendicular, they intersect to form four right angles. It also provides an example proof of theorem 3.2 using a two-column format.

1. Theorems About Perpendicular Lines

2. Comparing Types of Proofs Two-Column Proof Paragraph Proof Flow Proof Uses arrows to show the flow of the logical argument

3. Right Angle Congruence Theorem 1. Two Column Proof: All right angles are congruent. Given : 1 and 2 are right angles Prove : 1 ≅ 2 Statement Reason 1 and 2 are right angles Given m 1 = 90 o , m 2 = 90 o Definition of a right angle m 1 = m 2 Transitive property of equality 1 ≅ 2 Definition of congruent angles

4. Because angles 1 and 2 are right angles, their measures are equal to 90 o , by the definition of right angles. Hence by the transitive property of equality, the measure of angle 1 is equal to the measure of angle 2. By the definition of congruent angles, angle 1 is congruent to angle 2. 2. Paragraph Proof

5. 3. Flow Proof

6. Theorem 3.1 If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.

7. Theorem 3.2 If two sides of two adjacent acute angles are perpendicular, then the angles are complementary.

8. Theorem 3.3 If two lines are perpendicular, then they intersect to form four right angles.

9. Proof of Theorem 3.2 Prove : 1 + 2 are complementary Statement Reason AB BC Given ABC is a right angle Definition of perpendicular lines m ABC = 90 o Definition of a right angle m 1 + m 2 = m ABC Angle addition postulate m 1 + m 2 = 90 o Substitution property of equality 1 + 2 are complementary Definition of complementary angles

10. Practice and Homework Workbook: Exercise 3.2 Textbook: Exercise 3.2 p138: 1-27, odd