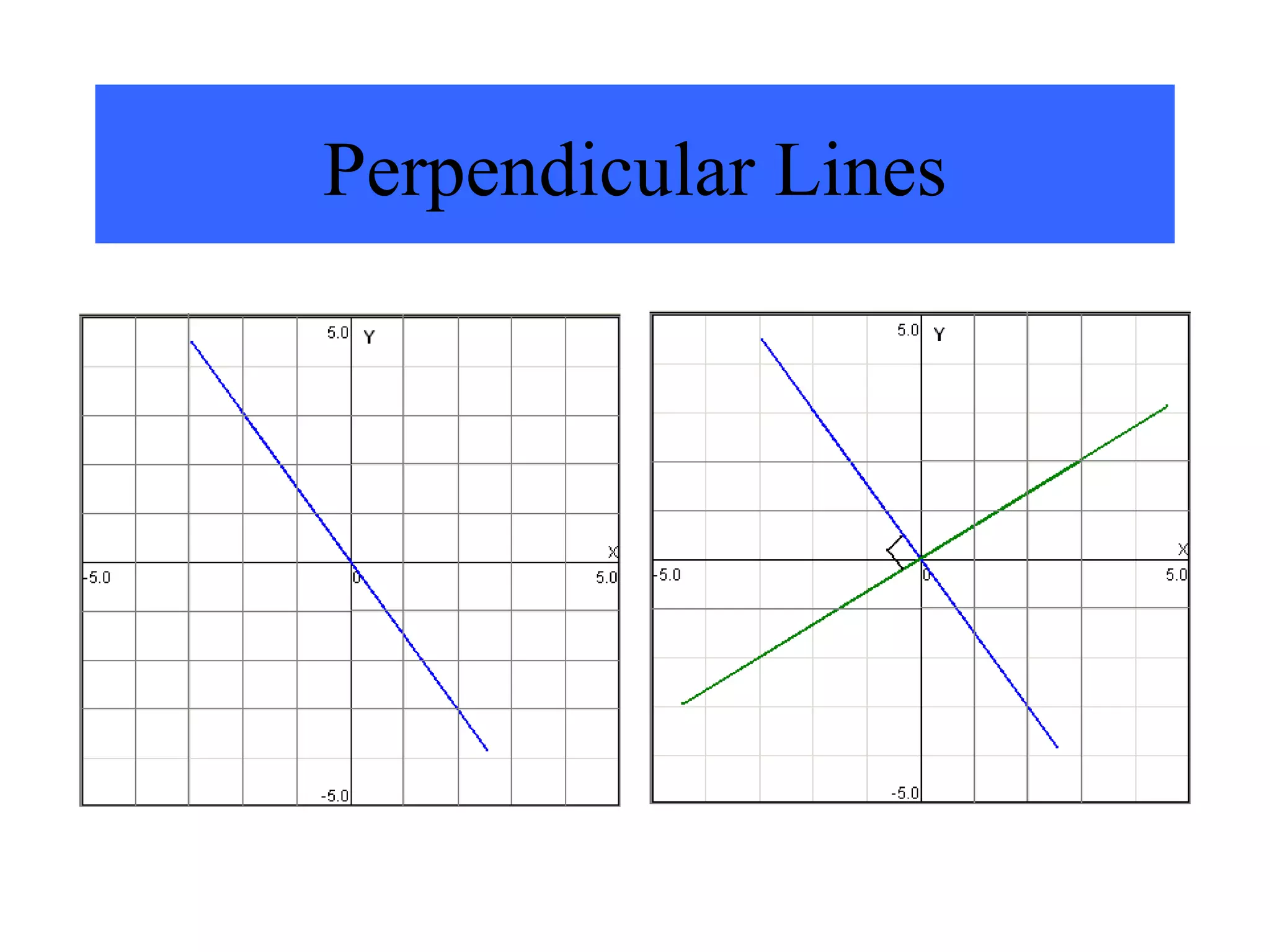
1) Parallel lines have the same slope. Perpendicular lines have slopes that are negative reciprocals of each other. 2) To determine if two lines are parallel or perpendicular, you calculate their slopes. If the slopes are equal, the lines are parallel. If the slopes are negative reciprocals, the lines are perpendicular. 3) To find the equation of a line parallel or perpendicular to a given line, you use the slope of the given line and the point-slope formula. For a parallel line, you use the same slope. For a perpendicular line, you use the negative reciprocal slope.

1. Parallel and Perpendicular Lines

2. If two non-vertical lines in the same plane have the same slope, then the lines are parallel . If two non-vertical lines in the same plane are parallel , then they have the same slope. Two horizontal lines in the same plane are parallel ; two vertical lines in the same plane are parallel . Parallel Lines: Concept

3. SOLUTION EXAMPLE 1 Write an equation of a parallel line Write an equation of the line that passes through (–3, –5) and is parallel to the line y = 3 x – 1. STEP 1 Identify the slope. The graph of the given equation has a slope of 3. So, the parallel line through (–3, –5) has a slope of 3. STEP 2 Find the y - intercept. Use the slope and the given point. y = m x + b Write slope-intercept form .

4. EXAMPLE 1 Write an equation of a parallel line y = 3 x + b – 5 = 3 ( –3 ) + b 4 = b Substitute 3 for m . Substitute  3 for x , and  5 for y . Solve for b . STEP 3 Write an equation. Use y = mx + b . y = 3 x + 4 Substitute 3 for m and 4 for b . Using the point (–3, –5)

5. GUIDED PRACTICE for Example 1 Write an equation of the line that passes through (–2, 11 ) and is parallel to the line y = –x + 5. y = –x + 9 ANSWER

6. Perpendicular Lines

7. If two non-vertical lines in the same plane have slopes that are negative reciprocals, then the lines are perpendicular . If two non-vertical lines in the same plane are perpendicular , then their slopes are negative reciprocals. A horizontal line and a vertical line in the same plane are perpendicular . Perpendicular Lines: Concept

8. EXAMPLE 2 Determine whether lines are parallel or perpendicular Determine which lines, if any, are parallel or perpendicular. Line a : y = 5 x – 3 Line b : x + 5 y = 2 Line c : –10 y – 2 x = 0 SOLUTION Find the slopes of the lines . Line a : The equation is in slope-intercept form . The slope is 5. Write the equations for lines b and c in slope-intercept form.

9. EXAMPLE 2 5 y = – x + 2 – 10 y = 2 x Determine whether lines are parallel or perpendicular Line a : m = 5. Line b : x + 5 y = 2 Line c : – 10 y – 2 x = 0 y = – x 1 5 x y = 2 5 1 5 + –

10. EXAMPLE 2 ANSWER Determine whether lines are parallel or perpendicular Lines b and c have slopes of – , so they are parallel. 1 5 Line a has a slope of 5, the negative reciprocal of – , so it is perpendicular to lines b and c . 1 5

11. GUIDED PRACTICE for Example 2 Determine which lines, if any, are parallel or perpendicular. Line a : 2 x + 6 y = –3 Line b : y = 3 x – 8 Line c : –1.5 y + 4.5 x = 6 ANSWER parallel: b and c ; perpendicular: a and b , a and c

12. SOLUTION EXAMPLE 3 Determine whether lines are perpendicular Line a : 12 y = –7 x + 42 Line b : 11 y = 16 x – 52 Find the slopes of the lines . Write the equations in slope-intercept form . The Arizona state flag is shown in a coordinate plane. Lines a and b appear to be perpendicular. Are they ? STATE FLAG

13. EXAMPLE 3 Determine whether lines are perpendicular Line a : 12 y = –7 x + 42 Line b : 11 y = 16 x – 52 ANSWER y = – x + 12 42 7 12 11 52 y = x – 16 11 The slope of line a is – . The slope of line b is . The two slopes are not negative reciprocals, so lines a and b are not perpendicular. 7 12 16 11

14. SOLUTION EXAMPLE 4 Write an equation of a perpendicular line Write an equation of the line that passes through (4, –5) and is perpendicular to the line y = 2 x + 3. STEP 1 Identify the slope. The graph of the given equation has a slope of 2. Because the slopes of perpendicular lines are negative reciprocals, the slope of the perpendicular line through (4, –5) is . 1 2 –

15. EXAMPLE 4 STEP 2 Find the y - intercept. Use the slope and the given point. Write slope-intercept form. Solve for b . STEP 3 Write an equation . y = mx + b Write slope-intercept form . Write an equation of a perpendicular line – 5 = – ( 4 ) + b 1 2 Substitute – for m , 4 for x , and – 5 for y . 1 2 y = m x + b – 3 = b y = – x – 3 1 2 Substitute – for m and –3 for b . 1 2

16. GUIDED PRACTICE for Examples 3 and 4 3. Is line a perpendicular to line b ? Justify your answer using slopes. Line a : 2 y + x = –12 Line b : 2 y = 3 x – 8 ANSWER 1 No; the slope of line a is – , the slope of line b is . The slopes are not negative reciprocals so the lines are not perpendicular. 2 3 2

17. GUIDED PRACTICE for Examples 3 and 4 4. Write an equation of the line that passes through (4, 3) and is perpendicular to the line y = 4 x – 7 . ANSWER y = – x + 4 1 4

18. Parallel lines have the same slope. m 1 = m 2 The slopes of perpendicular lines are negative reciprocals of each other. m 1 ． m 2 = -1 OR Summary

19. Homework Exercise 5.5 page 322: 1-35, Odd.