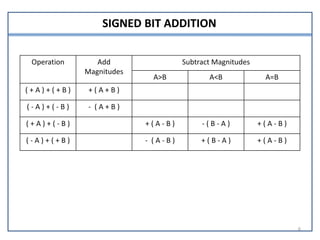
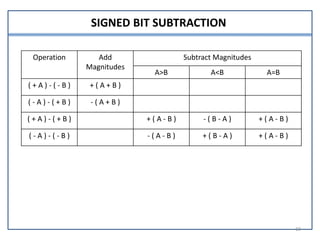
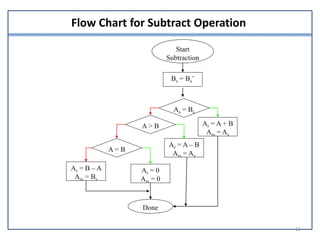
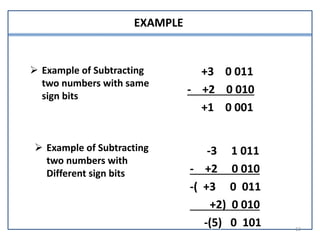
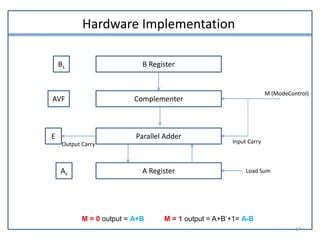
This document presents information on signed number representation and algorithms for signed addition and subtraction. It discusses signed magnitude, 1's complement, and 2's complement representations. It provides examples and flowcharts for the addition and subtraction algorithms in signed magnitude representation. The algorithms treat the signs and magnitudes separately. For hardware implementation, it shows how a parallel adder, complementer, and mode control can be used to perform signed addition and subtraction.

1. SARVAJANIK COLLEGE OF ENGINEERING AND
TECHNOLOGY
COMPUTER ENGINEERING DEPARTMENT
B. E.-II, CO-E, SEM-IV
(EVEN-2019)
ALA Presentation
on
“Signed Addition And Subtraction”
Subject Name : Computer Organisation(2140702)
Prepared and Presented by (Group No. : 14 )
Pathik Thakor (170420107557)
Jasmin Thummar (170420107558)
Uttam Thummar (170420107559)
Keyur Vadodariya (170420107561)
1

2. Overview
• Representation of Number
• Addition & Subtraction Algorithm
• Flow Chart
• Examples
• Hardware implementation
2

3. SIGNED BIT REPRESENTATION
Example: Represent +9 and -9 in 7 bit-binary number
Only one way to represent + 9 ==> 0 001001
Three different ways to represent - 9:
In signed-magnitude: 1 001001
In signed-1's complement: 1 110110
In signed-2's complement: 1 110111
Representation of both positive and negative numbers
- Following 3 representations
Signed magnitude representation
Signed 1's complement representation
Signed 2's complement representation
3

4. Sign-magnitude number
 A sign-magnitude
number Z can be
represented as (As, A)
where As is the sign of Z
and A is the magnitude
of Z.
 The leftmost position, As,
is the sign bit.
 The sign bit is either
positive = 0 or negative =
1
Number
Signed-
Magnitude
+3 0 11
+2 0 10
+1 0 01
+0 0 00
-0 1 00
-1 1 01
-2 1 10
-3 1 11
4

5. ADDITION ALGORITHM
When the sign of A and B are same, add the magnitudes and attach
the sign of A to the result.
Otherwise compare the magnitudes and subtract the smaller
number from the larger.
 Choose the sign of result to be same as A if A>B
 or the complement of sign of A if A<B
 if A=B subtract B from A and make the sign of result positive
5

6. SIGNED BIT ADDITION
Operation Add
Magnitudes
Subtract Magnitudes
A>B A<B A=B
( + A ) + ( + B ) + ( A + B )
( - A ) + ( - B ) - ( A + B )
( + A ) + ( - B ) + ( A - B ) - ( B - A ) + ( A - B )
( - A ) + ( + B ) - ( A - B ) + ( B - A ) + ( A - B )
6

7. Flow Chart for Addition Operation
Start Addition
As = Bs
Ar = A + B
Ars = As
A > B
Ar = A – B
Ars = As
A = B
Ar = 0
Ars = 0
Done
Ar = B – A
Ars = Bs
7

8. EXAMPLE
 Example of adding two
magnitudes when the
result is the sign of both
operands:
+3 0 011
+ +2 0 010
+5 0 101
-3 1 011
+ +2 0 010
-( +3 0 011
- 2) 1 010
-(1) 1 001
 Example of adding two
magnitudes when the
result is the sign of larger
magnitude
8

9. SUBTRACTION ALGORITHM
 When the sign of A and B are Different , add the magnitudes and
attach the sign of A to the result.
Otherwise compare the magnitudes and subtract the smaller
number from the larger.
 Choose the sign of result to be same as A if A>B
 or the complement of sign of A if A<B
 if A=B subtract B from A and make the sign of result positive
9

10. SIGNED BIT SUBTRACTION
Operation Add
Magnitudes
Subtract Magnitudes
A>B A<B A=B
( + A ) - ( - B ) + ( A + B )
( - A ) - ( + B ) - ( A + B )
( + A ) - ( + B ) + ( A - B ) - ( B - A ) + ( A - B )
( - A ) - ( - B ) - ( A - B ) + ( B - A ) + ( A - B )
10

11. Flow Chart for Subtract Operation
Ar = B – A
Ars = Bs
Start
Subtraction
Bs = Bs’
As = Bs
Ar = A + B
Ars = As
A > B
Ar = A – B
Ars = As
A = B
Ar = 0
Ars = 0
Done
11

12. EXAMPLE
 Example of Subtracting
two numbers with same
sign bits
+3 0 011
- +2 0 010
+1 0 001
-3 1 011
- +2 0 010
-( +3 0 011
+2) 0 010
-(5) 0 101
 Example of Subtracting
two numbers with
Different sign bits
12

13. Hardware Algorithm
13

14. Hardware Implementation
B Register
Complementer
Parallel Adder
A Register
Bs
E
AVF
As Load Sum
Input Carry
M (ModeControl)
Output Carry
M = 0 output = A+B M = 1 output = A+B’+1= A-B
14

15. EXAMPLE
+3 0 011
- +2 0 010
+( +3 0 011
-2) 1 110
+(1) 0 001
 Example of Subtracting
two numbers with
Different sign bits with
2’s complement
Arithmetic
+3 -> 0011
+2 -> 0010
-2 -> 2’scomp(“+2”)
-> 1110
15

16. 16