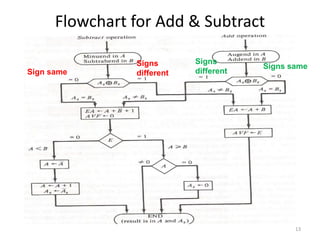
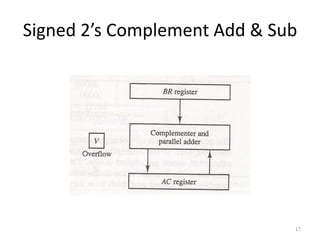
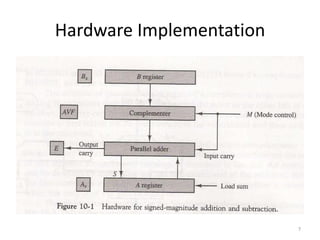
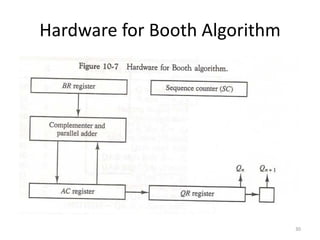
This document discusses different arithmetic operations like addition, subtraction, and multiplication in binary. It covers: 1) Representing negative numbers in signed magnitude and two's complement notation. Subtraction is performed by adding the number to the two's complement of the subtrahend. 2) Hardware implementation of addition and subtraction using registers, sign flip flops, and a parallel adder. Subtraction is achieved by adding the number to the two's complement using a mode control signal. 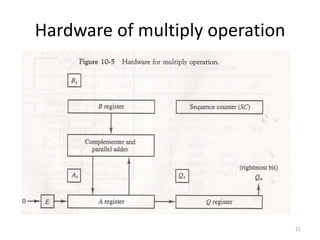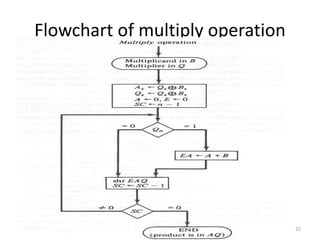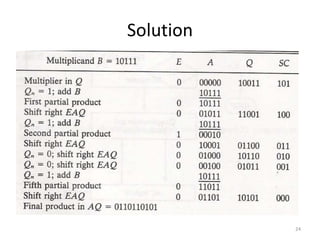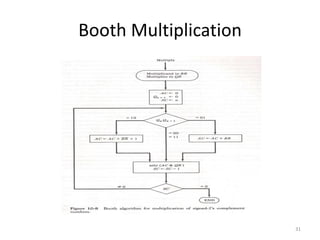3) The Booth algorithm for multiplying signed two's complement numbers, which involves conditionally adding or subtracting the multiplicand from the partial product based on the multiplier bits.

1. Arithmetic Operation
1

2. Addition and subtraction of Signed-
magnitude numbers
2

3. • In the above table, last column is needed to
prevent a negative zero.
• i.e. when 2 equal numbers are subtracted, the
result should be +0 not -0
3

4. Complement data
• suppose we want to find how -28 would be
expressed in two's complement notation.
• 1st we write out 28 in binary form: 0001 1100
• Then we invert the digits. 0 becomes 1, 1
becomes 0 i.e. 1110 0011
• Then we add 1.
• 1110 0100
• That is how one would write -28 in 8 bit
binary. 4

5. Complement data
+33 is represented as:
0010 0001
And -33 is represented as:
1101 1111 which is the 2’s complement of
0010 0001
5

6. Sign Bit
Leftmost bit of a binary number represents
Sign bit
0 for positive
1 for negative
If sign bit is 1, entire number is represented in
2’s complement form
6

7. Hardware Implementation
7

8. • Registers A and B
• Sign Flip Flops As and Bs
• Subtraction is done by adding A to the 2’s
complement of B
• Output carry is transferred to flip Flop E
• AVF(Add-overflow Flip Flop) holds overflow
bit when A and B are added.
8

9. • Addition A+B is done by parallel adder
• S (Sum) output of parallel adder is applied to
input of register A
• Complementer provides Output of B or
Complement of B(depending on state of Mode
control M)
• M signal also applied to input carry of adder.
When M=0, output of B is transferred to
Adder, Input carry is 0, output of adder= sum
A+B
9

10. • When M=1, 1’s complement of B is applied to
adder, input carry is 1, output S=A+B+1
(i.e equal to A plus 2’s complement of B)
Which is equal to subtraction A-B
10

11. Addition
• In addition, an augend and an addend are
added to find a sum.
In the following
6 + 3 = 9
6 is the augend,
3 is the addend
and 9 is the sum:
11

12. Subtraction
• In subtraction, a subtrahend is subtracted
from a minuend to find a difference.
• In the following:
9 – 3 = 6
• 9 is the minuend,
• 3 is the subtrahend,
• and 6 is the difference.
12

13. Flowchart for Add & Subtract
13
Sign same
Signs
different
Signs
different
Signs same

14. Flowchart for Add & Subtract:
Explanation
• 2 signs As and Bs are compared by EX-OR gate
• If output =0 , signs are same
• If output=1, signs are different
• If same signs in ADD (i.e. output=0) : Add
magnitudes
• If different signs in SUBTRACT(output=1) then
Add magnitudes as:
EA A+B
Here EA is register that combines E and A 14

15. • Carry in E after addition constitutes
OVERFLOW if it is =1
• Value of E is transferred to AVF
• If signs are different for ADD, & identical for
SUBTRACT, then MAGNITUDES ARE
SUBTRACTED
• i.e. add A to 2’s complement of B
• AVF cleared to 0(bcoz no overflow occurs in
subtraction)
15

16. E=1 means
• A>=B
• And number in A is correct result
E=0 means
A<B
Then take 2’s complement of value in A
A A+1
16

17. Signed 2’s Complement Add & Sub
17

18. Algo. For adding & subtracting numbers in
signed 2’s complement representation
18

19. MULTIPLICATION
• Multiplication
In multiplication, a multiplicand and
a multiplier are multiplied to find a product.
e.g. In the following equation,
6 x 3 = 18
6 is the multiplicand,
3 is the multiplier
18 is the product.
19

20. Multiplication
20

21. Hardware of multiply operation
21

22. Flowchart of multiply operation
22

23. Practice question 1
Question: Multiplicand= 23
Multiplier=19
Show the contents of E, A, Q, SC during
multiplication process.
23

24. Solution
24

25. Practice question 2
Show the contents of registers E, A, Q and SC
during the process of multiplication of 2 binary
numbers:
11111(multiplicand) and 10101(multiplier).
The signs are not included.
25

26. Solution
26
(final result in AQ)

27. BOOTH ALGORITHM FOR
MULTIPLICATION OF SIGNED 2’s
COMPLEMENT NUMBERS
27

28. Booth Algorithm
• Check multiplier bits and shift partial
product
• Before shifting, multiplicand may be
added/subtracted from partial product or left
unchanged according to following rules
28

29. Rules :
29

30. Hardware for Booth Algorithm
30

31. Booth Multiplication
31

32. Practice Question 1
Booth Multiplication
• Given multiplicand= -9 and multiplier= -13.
Show the step by step multiplication using
Booth Algorithm. Show the contents of AC,
QR, Qn+1 and SC.
32

33. solution
33
Final product stored in AC, QR i.e. 0001110101

34. Practice Question
Show the step by step multiplication process
using booth algorithm for multiplying following
numbers. Assume 5 bit registers that hold
signed numbers. The multiplicand in both cases
is +15
a. (+15) X (+13)
b. (+15) X (-13)
34

35. Solution (a)
35

36. Solution (b)
36