This document provides an extensive overview of radar basics, including fundamental concepts and various radar configurations, such as pulse and continuous wave radar. It covers essential components like antennas, transmitters, and receivers, detailing technologies like magnetrons, traveling wave tubes, and klystrons. Signal processing and applications of radar technology are also discussed, alongside the intricacies of radar measurements and operational theories.













































![SOLO
Receiver Equivalent Noise
Boltzman’s constant
Gain = G1
Noise Figure = F1
Gain = G2
Noise Figure = F2
Gain = Gi
Noise Figure = Fi
The gain of the receiver is iGGGG 21 ⋅=
The noise figure of the receiver is
i
i
GGG
F
GG
F
G
F
FF
2121
3
1
2
1
111 −
++
−
+
−
+=
A radar receiver usually has a pre-amplifier (1) characterized by a low noise figure
(F1) and by a high gain (G1) such that the effect of the noise of other amplifiers is
negligible and This is the Low Noise Amplifier (LNA).1FF ≈
The noise energy (white noise) at the Receiver is [ ]jouleFTkEN 0=
where
Kjoulek
/1038.1 23−
×=
The receiver consists of a number of amplifiers in cascade.
KT
2900 = room temperature
F receiver noise figure
Receiver Noise Power [ ]wattBFTkN 0=
B - Receiver Bandwidth Return to Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-66-320.jpg)



![Radar Equation
Radar Cross Section Definition
SOLO
- Target Radar Cross Section (RCS) [m2
]TGTσ
The incident Power Density (Irradiance) at the target is given by:
2 2 2
/i i i i iS E H H E watt m
µ ε
ε µ
= × = =
r r
The Power Density (Irradiance) intercepted and scattered
by the target is given by: [ ]i TGTS wattσ
The received Power Density (Irradiance) is defined as:
2 2 2
/r r r r rS E H H E watt m
µ ε
ε µ
= × = =
r r
Power scattered by the target in each steradian: ( ) [ ]/ 4 /i TGTS watt strσ π
Solid angle of receiver as seen from the target: [ ]2
/RCVRA R strΩ=
The received Power is given by:
[ ]2
4
i TGT RCVR
S A
watt
R
σ
π
The received Power is given also
by:
2
/r RCVRS A watt m
2
4
i TGT RCVR
r RCVR
S A
S A
R
σ
π
=
2
lim 4 r
TGT
R
i
S
R
S
σ π
→∞
=Since RCS is defined in the Far Field:](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-72-320.jpg)





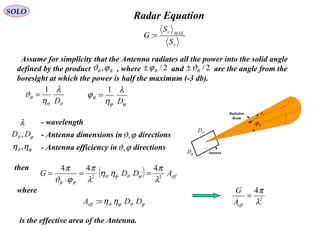
![Far away from the source of radiation (far field)
the electromagnetic fields and are perpendicular
to each other and to the direction of propagation,
and their amplitudes drop off inversely with the Range R.
E
r
H
r
( ) ( ) ( ) 10202101 constRERRERRER =⇒=
( ) ( ) ( ) 20202101 constRHRRHRRHR =⇒=
That means that the electromagnetic field acts as a spherical wave.
Accordingly the irradiance at a range R from an isotropic radiator (radiating uniformly
in all directions) is:
[ ]2
2
/
4
mwatt
R
P
HES rad
r
π
=×=
rr
0
0
0
0 EH
µ
ε
=
where < > means the time average.
A non-isotropic radiator will radiate more in some direction than in others, and the
maximal irradiation will be:
[ ]2
2
/
4
mwattG
R
P
HES rad
MAXMAXr
π
=×=
rr
where G is the Antenna Gain, a measure of the maximum radiation capability of
the Antenna.
SOLO Radar EquationIrradiation](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-85-320.jpg)

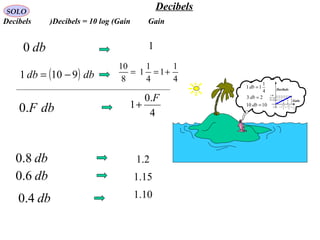
![Radar Equation
The Power Density (Irradiance) at the target is given by:
TRP
TRG
TRR
EV
Target
Transmitter
[ ]2
Pr
2
/
1
4
1
mW
LRL
GP
S
TGTXMTR
opagation
TGTTR
rTransmitte
TR
TRTR
r
→
→
=
π
- Transmitter Power [W]TRP
- Transmitter Antenna Gain in the Target directionTRG
- Transmitter Loss (XMTR+Antenna+Radome) ( > 1 )TRL
- Range Transmitter to Target [m2
]TRR
- Propagation Loss from Transmitter to Target ( > 1 )TGTTRL →
SOLO](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-88-320.jpg)
![Radar Equation
The Power reflected by the target in the receiver direction is:
[ ]WGA
LRL
GP
GASP
TGT
TGTTGT
TGTXMTR
opagation
TGTTRTR
rTransmitte
TR
TRTR
TGTTGTrTGT
σ
π
→
→
==
Pr
2
4
1
- Target Effective area in the Transmitter direction [m2
]TGTA
- Target Gain in the Receiver directionTGTG
- Propagation Loss from Target to Receiver ( > 1 )RCVRTGTL →
The Power Density [W/m2
] received at the Receiver is
[ ]2
Pr
2
/
1
4
1
mW
LR
Pp
RCVRTGT
opagation
RCVRTGTRCVR
TGTRCV
→
→
=
π
Target
Transmitter
Receiver
SOLO
- Target Radar Cross Section (RCS) [m2
]TGT TGT TGTA Gσ =](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-89-320.jpg)
![Radar Equation
[ ]2
Pr
2
Pr
2
/
1
4
11
4
1
mW
LR
GA
LRL
GP
p
RCVRTGT
opagation
RCVRTGTRCVR
TGTTGT
TGTXMTR
opagation
TGTTRTR
rTransmitte
TR
TRTR
RCVR
TGT
→
→
→
→
=
ππ σ
- Propagation Loss at the Receiver ( > 1 )RCVRL
The Power Density [W/m2
] received at the Receiver is
[ ]W
L
A
LR
GA
LRL
GP
LApP
ceiver
RCVR
RCVR
RCVRTGT
opagation
RCVRTGTRCVR
TGTTGT
TGTXMTR
opagation
TGTTRTR
rTransmitte
TR
TRTR
RCVRRCVRRCVRCVR
TGT
RePr
2
Pr
2
1
4
11
4
1
/
→
→
→
→
=
=
ππ σ
The Power [W/m2
] received at the Receiver is
- Effective area in the Receiver Antenna [m2
]RCVRA
SOLO](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-90-320.jpg)
![Radar Equation
[ ]W
L
G
LR
GA
LRL
GP
P
ceiver
RCVR
RCVR
RCVRTGT
opagation
RCVRTGTRCVR
TGTTGT
TGTXMTR
opagation
TGTTRTR
rTransmitte
TR
TRTR
RCVR
TGT
Re
2
Pr
2
Pr
2
4
1
4
11
4
1
π
λ
ππ σ
→
→
→
→
=
the Power [W/m2
] received at the Receiver is
π
λ
4
2
RCVR
RCVR
G
A =
( )
[ ]W
LLLLRR
GGP
P
RCVRRCVRTGTTGTTRTRRCVRTR
TGTRCVRTRTR
RCVR
→→
= 223
2
4π
σλ
Using
or
SOLO](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-91-320.jpg)
![Radar Equation
[ ]W
L
G
LR
GA
LRL
GP
P
ceiver
RCVR
RCVRTGT
opagation
TGTTR
TGTTGT
TGTXMTR
opagation
TGTTR
rTransmitte
TR
TR
RCVR
TGT
Re
2
Pr
2
Pr
2
4
1
4
11
4
1
π
λ
ππ σ
→
→
→
→
=
the Power [W/m2
] received at the Receiver is
( )
[ ]W
LLLR
GP
P
RCVRTGTTRTR
TGTTR
RCVR 243
22
4 →
=
π
σλ
or
SOLO
,RRR RCVRTR ==Collocated Transmitter & Receiver
with a Common Antenna
RCVRTGTTGTTR LL →→ =
GGG RCVRTR ==
Return to Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-92-320.jpg)






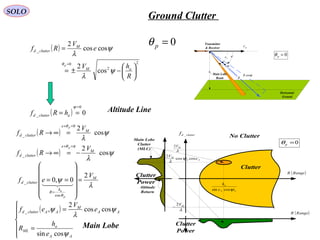
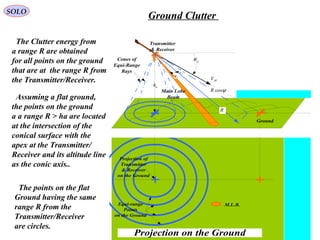
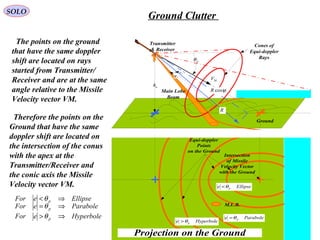
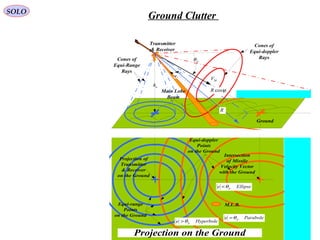
![ah
MV
pθ
e
ψ
R
ψcosR
Ae
Aψ
Horizontal
Ground
Main Lobe
Beam
Transmitter
& Receiver
πθθπθ ≤+≤⇒−≤≤− ppp ee 0
Define a ray R from transmitter
to ground, defined by the angles
e,ψ, relative to Missile velocity
vector.
VM is the Missile (transmitter)
velocity vector, having an angle
θp with the horizontal plane.
( )
≤≤−
≤+≤
≥
+
=
2/2/
0
cossin
πψπ
πθ
ψθ
p
a
p
a
e
hR
e
h
R ( )
ψ
θ 22
cos
1cos
R
h
e a
p −±=+
The doppler frequency shift along the ray R is given by:
( ) ( ) ( )[ ]
ψ
θψθ
λ
ψθθθθ
λ
ψ
λ
cos
sincoscos
2
cossinsincoscos
2
coscos
2
2
2
_
aa
p
a
p
M
pppp
MM
clutterd
h
R
R
h
R
hV
ee
V
e
V
Rf
≥
+
−±=
+++==
SOLO
Ground Clutter](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-100-320.jpg)
![( )
( ) ( )[ ]
+
−±=
+++=
=
R
h
R
hV
ee
V
e
V
Rf
a
p
a
p
M
pppp
M
M
clutterd
θψθ
λ
ψθθθθ
λ
ψ
λ
sincoscos
2
cossinsincoscos
2
coscos
2
2
2
_
( ) p
M
aclutterd
V
hRf θ
λ
ψ
sin
20
_
=
==
( ) ψθ
λ
θ
coscos
20
_ p
M
e
clutterd
V
Rf
p =+
=∞→
( ) ψθ
λ
πθ
coscos
2
_ p
M
e
clutterd
V
Rf
p
−=∞→
=+
Altitude Line
λ
ψ
θ
M
h
R
clutterd
V
ef
p
a
2
0,0
cos
_ =
==
=
clutterdf _
( )RangeR
( )RangeR
Clutter
No Clutter
Clutter
Power
Clutter
Power
Main Lobe
Clutter
(MLC)
Altitude
Return
λ
MV2
p
MV
θ
λ
cos
2
AA
M
e
V
coscos
2
ψ
λ
p
MV
θ
λ
sin
2
p
MV
θ
λ
cos
2
−
( ) ApA
a
e
h
ψθ cossin +
( )
( )
+
=
=
ApA
a
ML
AA
M
AAclutterd
e
h
R
e
V
ef
ψθ
ψ
λ
ψ
cossin
coscos
2
,_
Main Lobe
ah
MV
pθ
e
ψ
R
ψcosR
Ae
Aψ
Horizontal
Ground
Main Lobe
Beam
Transmitter
& Receiver
SOLO
Ground Clutter](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-101-320.jpg)

![SOLO
Ground Clutter
Illuminated Ground Area Resolution Cell : Beam Limitted Case
The Main Beam Clutter (Ground) Area in Range Resolution Cell when
is give (see Figure) by:
( ) ( ) pazcRA θϕτ cos/2/tan2/2Clutter =
Ground
Main Lobe
Beam
Transmitter
& Receiver
( ) ( )2//2/tan2tan τϕθ cR elp <
R – range to ground along beam center
φaz – angular beam width in azimuth
φel – angular beam width in elevation
θp –beam grazing angle
τ – pulse width [sec]
c – speed of light 3 108
m/sec
( )Clutter Clutter pAσ σ θ=
σ – ground reflectivity as function of
grazing angle](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-108-320.jpg)
![SOLO
Clutter
Illuminated Volume Resolution Cell (Pulse Limitted)
The Volume Clutter in Range Resolution Cell is give (see Figure) by:
( )2/
4
2
Clutter τϕϕ
π
cRV elaz=
R – range to ground along beam center
φaz – angular beam width in azimuth
φel – angular beam width in elevation
τ – pulse width [sec]
c – speed of light 3 108
m/sec
Main Lobe
Beam
Transmitter
& Receiver
Choose scatters on the main beam center Groundkk RRuntilkRkR ≥=∆= ,2,1
RADAR
I
k
f
c
where
sV
f =
⋅
= λ
λ
12
r
Their Doppler is given by
According to Range and Doppler of each scatter determine the Range-Doppler cell (i,j) for the
scatter.](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-111-320.jpg)



![SOLO
Multipath Return – Doppler Discrimination
The Target Range-Rate to Seeker is
( )22
ITIT
IITTITIT
hhX
hhhhXX
R
−+
++
=
−
−−
Let compute
Clutter
The Range-Rate of the Mirror of Target to Seeker is
( )( ) ( )
( )
( )
( )
( )
( )[ ] ( )[ ] Mi
Mi
IT
ITITITIT
IITTITITIT
ITIT
IITTITIT
ITIT
IIiTTITIT
MMM
RR
RR
hh
hhXhhX
hhhhXXhh
HHX
HHHHXX
HHX
HHHHXX
RRRRRR
4
4
2222
2
22
2
22
2
22
=
++−+
++
=
=
++
++
−
−+
++
=−=+−
−−
−−
−
−−
−
−−
0
24
3
2
>≈
+
=−
≈+
M
IT
RRR
M
M
M
IT
Mi RR
R
hh
RR
RR
RR
hh
RR
M
..
2
3
GDRR
R
hh
RR M
IT
M ≤≈− If we cannot distinguish between
Target and Target’s Mirror
..
2
3
GDRR
R
hh
RR M
IT
M >≈−
If we can distinguish between
Target and Target’s Mirror and we don’t have a
Multipath problem.
( )22
ITIT
IITTITIT
M
hhX
hhhhXX
R
++
++
=
−
−−
Assume that Target & Mirror Target are in the same Range Gate.
Multipath
Target Return
Target
Ground
A/C
RADAR
Target Multipath Return](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-115-320.jpg)

![SOLO
Multipath Return – Signal Power
Assume that The Target and it’s Mirror can be represented each
by Nsc scatters ( k=1,Nsc)
Clutter
The Mirror signal received by the Seeker from scatter k passes
three paths:
TGTXMTR
opagation
TGTTRk
rTransmitte
TR
trXmtr
LRL
GP
→
→
Pr
2
1
4
1
π1. Transmitted power from Seeker to Target Scatter k at the distance Rk:
2. Reflected by the target scatter k and reaching the ground at the distance ( ) ( )[ ] 2/122
_1 TkIIT
TkI
Tk
k hhX
hh
h
R ++
+
=
GNDTGT
opagation
GNDTGTk
TGTTGT
LR
GA
TGT
→
→
Pr
2
1
1
4
1
πσ
3. Reflected by the ground and reaching the Seeker at the distance ( ) ( )[ ] 2/122
_2 TkIIT
TkI
I
k hhX
hh
h
R ++
+
=
ReceivernPropagatio
2
2
1
4
1
RCVR
RCVR
GNDTGT
RCVRGNDk
GND
L
A
LR
→
→π
σ
π
λ
4
2
RCVR
RCVR
G
A =
Multipath
Target Return
Target
Ground
A/C
RADAR
Target Multipath Return](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-117-320.jpg)
![SOLO
Multipath Return – Signal Power
Therefore the received power from the k scatter mirror is:
Receiver
2
nPropagatio
2
2
Pr
2
1
Pr
2
1
4
1
4
11
4
11
4
1
RCVR
RCVRant
GNDTGT
RCVRGNDk
GND
GNDTGT
opagation
GNDTGTk
kScatterkScatter
TGTXMTR
opagation
TGTTRk
rTransmitte
TR
antXmtr
M
L
GG
LRLR
GA
LRL
GP
P
kScatter
k
π
λ
π
σ
ππ
σ
→
→
→
→
→
→
=
Clutter
( ) ( )[ ] 2/122
_1 TkIIT
TkI
Tk
k hhX
hh
h
R ++
+
= ( ) ( )[ ] 2/122
_2 TkIIT
TkI
I
k hhX
hh
h
R ++
+
=
( )
( )
( )( ) ( )
++
+++++
−=Σ ∑=
Σ
c
cj
gG
L
GG
Pji
jiN
k
ClutterkElkAzproc
trver
Rcvr
Xmtr
k2k1k
k2k1kk2k1k,
1 k2k1k
kscatter
proc
Targ
3
2
0
2
TargetMultipath
RRR
RRRRRR
2exp
RRR
,
L4
,
π
σσεε
π
λ
( )
( )
2
2
2
1
2
2Targ
3
2
0
2
,
4 kkk
ClutterkScatterkElkAz
proc
proc
trver
Rcvr
XmtrM
RRR
g
L
G
L
GG
PP k
σσεε
π
λ Σ
=
or:
where: ( )kElkAzant gGG εε ,0 Σ=
RCVRRCVRGNDGNDTGTTGTTRTRtrver LLLLLL →→→=
proc
proc
RcvrRCVR
L
G
GG
Targ
=
The Target Multipath received signal is obtained by integration (summation) of the
signals from the same range-doppler cell (i,j):
in the same way:
( )
( )
( )( ) ( )
++
+++++
−=∆ ∑=
∆
c
cj
gG
L
GG
Pji
jiN
k
ClutterkElkAzElAzproc
trver
Rcvr
Xmtr
k2k1k
k2k1kk2k1k,
1 k2k1k
kscatter,
proc
Targ
3
2
0
2
Az/ElTargetMultipath
RRR
RRRRRR
2exp
RRR
,
L4
,
π
σσεε
π
λ
Return to Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-118-320.jpg)










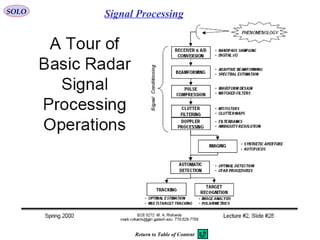







![SOLO
Windowing
Rectangular [ ]
≤≤
=
otherwise
Mn
nw
,0
0,1
Bartlett
(triangular) [ ]
≤<−
≤≤
=
otherwise
MnMMn
MnMn
nw
,0
2/,/22
2/0,/2
Hanning
Hammming
[ ]
( )
≤≤−
=
otherwise
MnMn
nw
,0
0,/2cos5.05.0 π
[ ]
( )
≤≤−
=
otherwise
MnMn
nw
,0
0,/2cos46.054.0 π
Blackman [ ]
( ) ( )
≤≤+−
=
otherwise
MnMnMn
nw
,0
0,/4sin08.0/2cos5.042.0 ππ
Julius Ferdinand von Hann (1839 -1921)
Richard Wesley Hamming (1915 –1998)
Signal Processing](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-142-320.jpg)
![SOLO
Windowing (continue – 1)
cosine
[ ]
≤≤<
−
−
=
otherwise
Mn
M
Mn
nw
,0
0&5.0
2/
2/
2
1
exp
2
σ
σ
Lanczos
[ ]
≤≤
−
=
otherwise
Mn
M
n
nw
,0
0,1
2
sinc
Gauss
[ ]
≤≤
=
−
=
otherwise
Mn
M
n
M
n
nw
,0
0,sin
2
cos
πππ
[ ]
( )
≤≤
−−
=
otherwise
Mn
I
M
n
I
nw
,0
0,
1
2
1
0
2
0
α
α
Kaiser
α=2π
α=3π
Signal Processing](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-143-320.jpg)
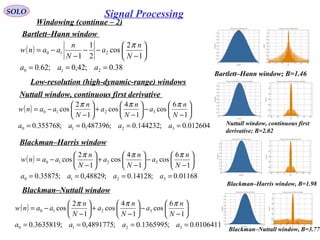
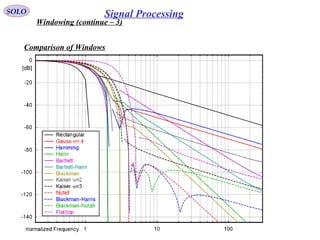
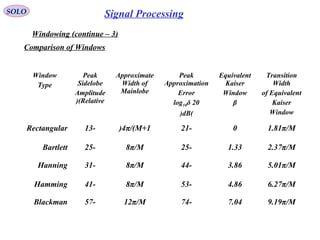
![SOLO
Windowing (continue – 3)
Dolph-Chebyshev window
( ) ( )[ ]
( )
( )[ ]
( ) ( )4,3,2,10cosh
1
cosh
1,,2,1,0,
coshcosh
coscoscos
1
1
1
≈
=
−=
=
=
−
−
−
αβ
β
π
β
ω
ω
α
N
Nk
N
N
k
N
W
WIDFTnw
k
k
The α parameter controls the side-lobe level via the formula:
Side-Lobe Level in dB = - 20 α
The Dolph-Chebyshev Window (or Dolph window) minimizes the Chebyshev norm of
the side lobes for a given main lobe width 2 ωc:
( ) ( ){ }ωωω WWsidelobes cwwww >=∞= ∑
=
∑
maxmin:min 1,1,
The Chebyshev norm is also called the L - infinity norm, uniform norm, minimax
norm, or simply the maximum absolute value.
Signal Processing](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-145-320.jpg)

![SOLO Signal Processing
Generation of Σ , ΔAz, ΔEl Range – Doppler Maps (continue – 1)
The received signal from the scatter k is:
( ) ( )[ ] ( ) ( )ttTktttTkttfCts ddkdk
r
k
r
k ++≤≤++−= τθπ2cos
Ck
r
– amplitude of received signal
td (t) – round trip delay time given by ( )
2/c
tRR
tt kk
d
+
=
θk – relative phase
The received signal is down-converted to base-band in order to extract the quadrature
components. More precisely sk
r
(t) is mixed with: ( ) [ ] τθπ +≤≤+= TktTktfCty kkk 2cos
After Low-Pass filtering the quadrature components of Σk, ΔAz k or ΔEl k signals are:
( ) ( )
( ) ( )
=
=
tAtx
tAtx
kkQk
kkIk
ψ
ψ
sin
cos
( ) ( )
+−≅−=
c
tR
c
R
fttft kk
kdkk
22
22 ππψ
The quadrature samples are given by:
( ) ( )
+−≅=
c
tR
c
R
fjAjAtX kk
kkkkk
22
2expexp πψ
Ak - amplitude of Σk, ΔAz k or ΔEl k signals
ψk - phase of Σk, ΔAz k or ΔEl k signals
( )
+−
+≅+=
c
tR
c
R
fAj
c
tR
c
R
fAxjxtX kk
kk
kk
kkQkIkk
22
2sin
22
2cos ππ](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-157-320.jpg)











![SOLO SEARCH & DETECT MODE
Computation of the Σ Range-Doppler Map, chooses the Detection Threshold
and policy (continue – 2).
DOPPLER
WINDOW
R W
A I
N N
G D
E O
W
R G
A A
N T
G E
E S
DOPPLER
FILTERS
S cells
CFAR
Window
R∆
f∆
Target
Uncertainty
Window
( ) ( ) ( )[ ]∑
∗
+ Σ⋅Σ=
n
j Window
CFARNoiseClutter jiji
n
iC ,,
1
Guard
(Gap)
Window
• Computation of Clutter + Noise Threshold
• Coherent Detection:
( ) ( )
( ) ( ) ClutterThjiNiCIf
ClutternoThjiNiCIf
NoiseClutter
NoiseClutter
⇒+>
⇒+≤
+
+
1,
1,
( ) NoiseThNjiS +≥
Window
yUncertaint
Target,
( ) ( ) ( )[ ]∑
∗
+ Σ⋅Σ=
n
j Window
CFARNoiseClutter jiji
n
iC ,,
1
1. If no Clutter declare a Detection in the (i,j) cell of the Target Window if
ThNoise is chosen to assure a predefined
Probability of Detection pd and of False Alarm pFA
( ) NoiseClutterNoiseClutter ThCjiS ++ +≥
Window
yUncertaint
Target,
2. If Clutter declare a Detection in the (i,j) cell of the Target Window if
ThNoise is chosen to assure a predefined
Probability of Detection pd and of False Alarm pFA](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-169-320.jpg)






















![SOLO Anti – Ballistic Missiles
Sea-Based X-Band Radar
Sea-Based X-Band Radar is a floating, self-propelled,
mobile radar station designed to operate in high winds
and heavy seas. It is part of the United States
Government's Ballistic Missile Defense System.
The Sea-Based X-Band Radar is mounted on a 5th
generation Norwegian-designed, Russian-built CS-50
semi-submersible twin-hulled oil-drilling platform.
Conversion of the platform was carried out at the
AMFELS yard in Brownsville, Texas; the radar mount
was built and mounted on the platform at the Kiewit
yard in Ingleside, Texas, near Corpus Christi. It will be
based at Adak Island in Alaska but can roam over the
Pacific Ocean to detect incoming ballistic missiles.
ST. LOUIS, Jan. 10, 2006 -- Boeing [NYSE: BA]
announced today the arrival in Hawaii of the Sea-
Based X-Band Radar (SBX) built for the U.S. Missile
Defense Agency. This marks an interim stop in the
vessel's transport operation, originating in the Gulf
of Mexico and maneuvering through the Straits of
Magellan, ultimately destined for Adak, Alaska.
http://cryptome.sabotage.org/sbx1-birdseye.htm
Radars for Ballistic Missile Defense
Return to Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-197-320.jpg)



















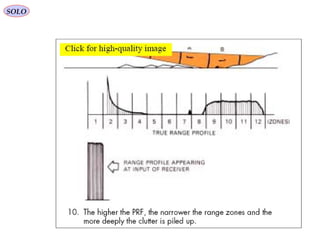

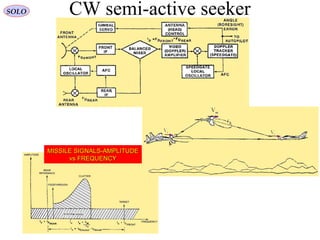
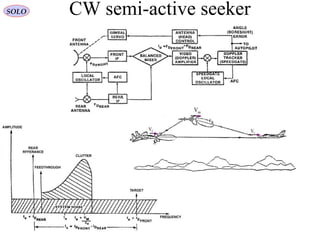
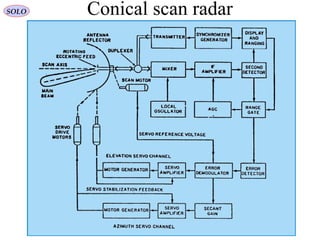







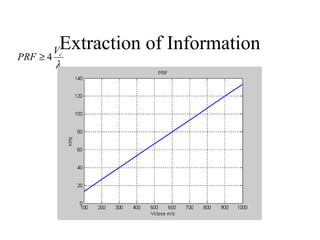


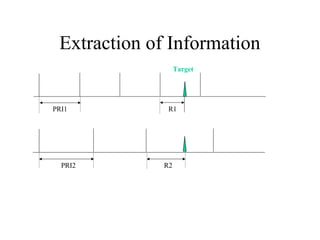

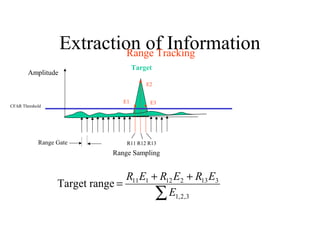
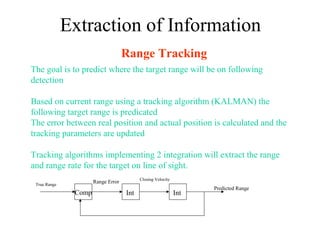
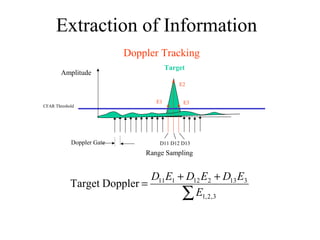


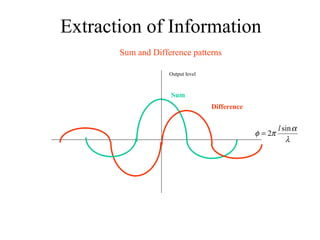

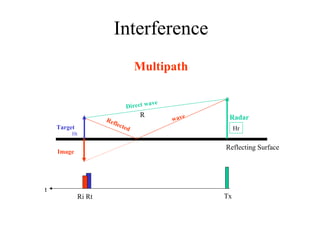



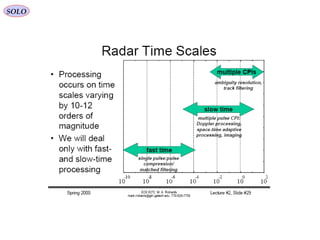
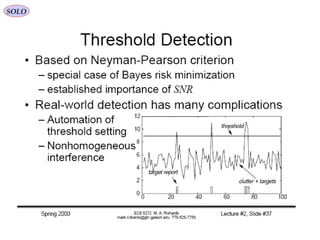


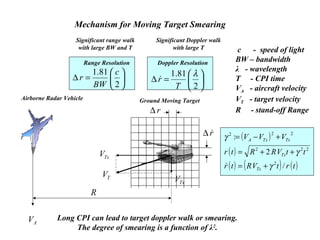


![Range & Doppler Measurements in RADAR SystemsSOLO
The transmitted RADAR RF
Signal is:
( ) ( ) ( )[ ]ttftEtEt 0000 2cos ϕπ +=
E0 – amplitude of the signal
f0 – RF frequency of the signal
φ0 –phase of the signal (possible modulated)
The returned signal is delayed by the time that takes to signal to reach the target and to
return back to the receiver. Since the electromagnetic waves travel with the speed of light
c (much greater then RADAR and
Target velocities), the received signal
is delayed by
c
RR
td
21 +
≅
The received signal is: ( ) ( ) ( ) ( )[ ] ( )tnoisettttftEtE ddr +−+−= ϕπα 000 2cos
To retrieve the range (and range-rate) information from the received signal the
transmitted signal must be modulated in Amplitude or/and Frequency or/and Phase.
ά < 1 represents the attenuation of the signal](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-261-320.jpg)
![Range & Doppler Measurements in RADAR SystemsSOLO
The received signal is:
( ) ( ) ( ) ( )[ ] ( )
( ) ( ) ( )tnoise
c
RR
tRRtftE
tnoisettttftEtE
fc
ddr
+
+
−++−=
+−+−=
=
21
21
0
000
/
000
2
2cos
2cos
00
ϕ
λ
π
πα
ϕπα
λ
If we consider only (c = speed of light) then the frequency of the electromagnetic
wave that reaches the receiver is given by:
c
td
Rd
<<
+
−≈
+
+−=
+
−+
+
−=
c
td
Rd
td
Rd
f
c
td
Rd
td
Rd
ud
d
ff
c
RR
t
c
RR
tf
td
d
f
21
0
21
0~
00
2121
0
1
2
1
2
2
1
ϕ
π
ϕπ
π
λ
+
−=
td
Rd
td
Rd
fd
21
is the doppler frequency shift at the receiver
Christian Johann Doppler first observed the effect in acoustics.](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-262-320.jpg)
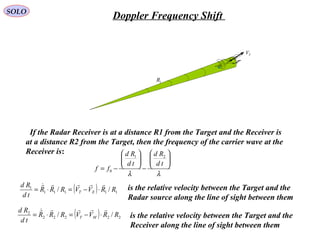
![Matched Filters in RADAR SystemsSOLO
α MV
R
EV
Target
Transmitter&
Receiver
The transmitted RADAR RF
Signal is:
( ) ( ) ( )[ ]ttftEtEt θπ += 00 2cos
( )
c
tR
td
02ˆ ≅
Since the received signal preserve the envelope shape of the known transmitted signal
we want to design a Matched Filter that will distinguish the signal from the receiver noise.
the received signal is: ( ) ( ) ( ) ( )[ ] ( )tnoisetttffttEtE dDdr +−++−≈ ˆˆ2cosˆ 00 θπα
Scaled Down
In Amplitude
Two-Way
Delay
Possible
Phase ModulationDoppler
Frequency
( ) ( )
λ
λ
0
/
0
0 22ˆ
0 tR
f
c
tR
f
fc
D
−=−≅
=
For R1 = R2 = R we obtain that](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-264-320.jpg)
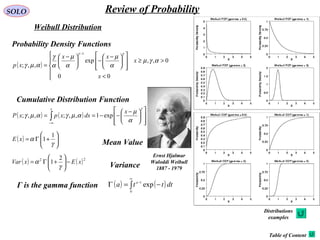
![SOLO Review of Probability
Exponential Distribution
( )
( )
<
≥−
=
00
0exp
;
x
xx
xp
λλ
λ
( ) ( )
( )
( ) ( )
λ
λλ
λλ
λλ
1
expexp
exp
0
0exp
0
=−+−−=
−=
∫
∫
∞
∞
=
−=
∞
dxxxx
dxxxxE
xu
dxxdv
( ) ( ) ( ) 2
22 1
λ
=−= xExExVar
( ) ( )[ ] ( ) ( )
( )[ ]
1
0
0
1exp
expexpexp
−∞
∞
−=−
−
=
−==Φ ∫
λ
ω
λω
λω
λ
λλωωω
j
xj
j
dxxxjxjEX
Probability Density Functions
Cumulative Distribution Function
Mean Value
Variance
Moment Generating Function
( ) ( )
( )
<
≥−−
=−= ∫∞−
00
0exp1
exp;
x
xx
dxxxP
x
λ
λλλ
( ) ( ) 2
0
2
2
22 2
λω ω
=
Φ
=
=
d
d
jxE X
Distributions
examples
Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-265-320.jpg)
![SOLO Review of Probability
Chi-square Distribution
( )
( )
( )
( )
( )
<
≥−
Γ=
−
00
02/exp
2/
2/1
;
2/2
2/
x
xxx
kkxp
k
k
( ) kxE =
( ) kxVar 2=
( ) ( )[ ]
( ) 2/
21
exp
k
X
j
xjE
−
−=
=Φ
ω
ωω
Probability Density Functions
Cumulative Distribution Function
Mean Value
Variance
Moment Generating Function
( )
( )
( )
<
≥
Γ=
00
0
2/
2/,2/
;
x
x
k
xk
kxP
γ
Γ is the gamma function ( ) ( )∫
∞
−
−=Γ
0
1
exp dttta a
( ) ( )∫ −= −
x
a
dtttxa
0
1
exp,γγ is the incomplete gamma function
Distributions
examples](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-266-320.jpg)
![SOLO Review of Probability
Student’s t-Distribution
( ) ( )[ ]
( ) ( )( ) 2/12
/12/
2/1
; +
+Γ
+Γ
= ν
ννπν
ν
ν
x
xp
( )
=
>
=
1
10
ν
ν
undefined
xE
( )
( )
∞
>−
=
otherwise
xVar
22/ ννν
Probability Density Functions
Cumulative Distribution Function
Mean Value
Variance
Moment Generating Function not defined
( ) ( )[ ]
( )
∑
∞
=
−
+
Γ
+Γ
+=
0
2
!
2
3
2
1
2
1
2/
2/1
2
1
;
n
n
n
nn
n
x
x
xP
ν
ν
ννπ
ν
ν
Γ is the gamma function ( ) ( )∫
∞
−
−=Γ
0
1
exp dttta a
( ) ( ) ( ) ( )121: −+++= naaaaa n L
It get his name after W.S. Gosset that wrote
under pseudonym “Student”
William Sealey
Gosset
1876 - 1937
Distributions
examples
Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-267-320.jpg)
![SOLO Review of Probability
Uniform Distribution (Continuous)
( )
>>
≤≤
−=
bxxa
bxa
abbaxp
0
1
,;
( )
2
ba
xE
+
=
( ) ( )
12
2
ab
xVar
−
=
( ) ( )[ ]
( ) ( )
( )abj
ajbj
xjE
−
−
=
=Φ
ω
ωω
ωω
expexp
exp
Probability Density Functions
Cumulative Distribution Function
Mean Value
Variance
Moment Generating Function
( )
>
≤≤
−
−
>
=
bx
bxa
ab
ax
xa
baxP
1
0
,;
Distributions
examples
Moments
Table of Content](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-268-320.jpg)

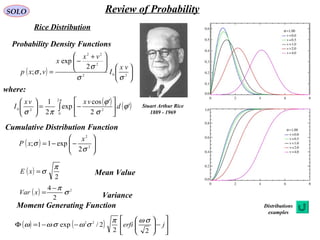
![SOLO Review of Probability
Rice Distribution
The Rice Distribution applies to the statistics of the envelope of the output of a bandpass
filter consisting of signal plus noise.
Example of Rice Distribution
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )[ ] ( ) ( )[ ] ( )tAtntAtn
ttnttntAtnts
SC
SC
00
000
sinsincoscos
sincoscos
ωϕωϕ
ωωϕω
−++=
+++=+
X = nC (t) and Y = nS (t) are gaussian random variables, with zero mean and the same
variances σ2
and φ is the unknown but constant signal phase.
Define the output envelope R and phase Θ:
( )[ ] ( )[ ]
( )[ ] ( )[ ]{ }ϕϕ
ϕϕ
cos/sintan
sincos
1
22
AtnAtn
AtnAtnR
CS
SC
+−=Θ
−++=
−
( ) ( ) ( ) ( )
( )
222
22
22
2
2
2
22
cos
exp
2
exp
22
sin
exp
2
cos
exp,,
σπ
θ
σ
θϕ
σ
σπσ
ϕ
σ
ϕ
θθ
drdrrAAr
ydxdAyAx
ydxdyxpdrdrp XYR
+
−
+
−=
−
−
+
−==Θ
Solution
( ) ( ) ( ) ( )∫∫ +
+
−
+
−== Θ
ππ
θϕ
σ
θϕ
σπσ
θθ
2
0
222
222
0 2
cos
exp
22
exp, d
rArAr
drprp RR](https://image.slidesharecdn.com/1-radarbasic-partii-150115073149-conversion-gate01/85/1-radar-basic-part-ii-272-320.jpg)