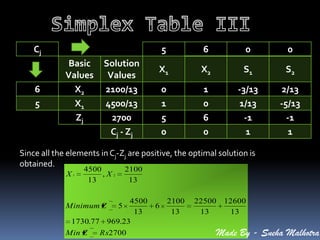
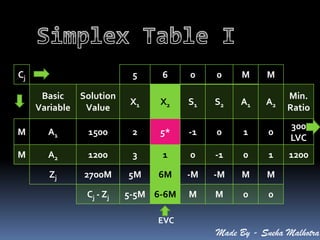
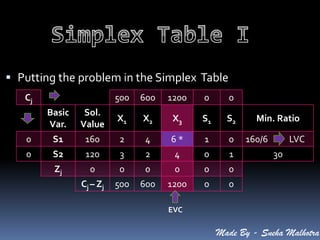
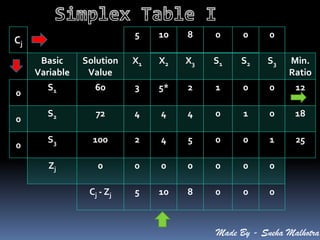
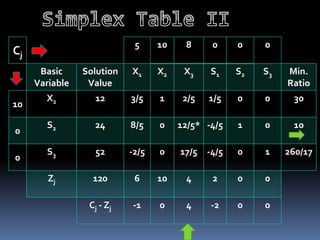
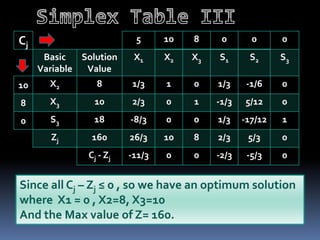
The document describes an optimization problem where a company manufactures 3 products (A, B, C) using precious metals as inputs. The company aims to maximize total profit given daily allotments of platinum and gold. The problem is formulated as a linear programming problem to determine the optimal production quantity of each product that maximizes profit. The simplex method is applied to solve the LPP and determine the maximum profit of Rs. 32,800 can be achieved by producing 8 units of product A and 24 units of product C.

1. Made by:
Sneha Malhotra
B.Com. 3rd yr

2. Made By - Sneha Malhotra

3. A company manufactures 3 types of parts which use precious
metals platinum and gold. Due to shortage of these precious
metals, the govt. regulates the amount that may be used per
day.The relevant data with respect to supply requirements
and profit are shown below:
Daily allotments of platinum & gold are 160 gm and 120 gm
respectively. How should the company divide the supply of
precious metals? What is the optimum profit?
Product Platinum per unit (gm) Gold per unit
(gm)
Profit per unit
(Rs.)
A 2 3 500
B 4 2 600
C 6 4 1200
Made By - Sneha Malhotra

4.  FORMULATION OF LPP
Maximize Z= 500 X1 + 600 X2 + 1200 X3
Subject to 2X 1 + 4X2 + 6X3 ≤ 160
3X1 + 2X2 + 4X3 ≤ 120
Where X1 , X2, X3 ≥ 0
Made By - Sneha Malhotra

5. ADDING SLACK VARIABLES ;S1 and S2
Maximize Z= 500X1 + 600X2 + 1200X3+0S1 + 0S2
Subject to: 2X1 + 4X2 +6X3 +1S1 +0S2= 160
3X1 + 2X2 + 4X3 + 0S1 + 1S2 =120
Where X1 , X2, X3 and S1, S2 ≥ 0
Made By - Sneha Malhotra

6.  Putting the problem in the Simplex Table
Cj 500 600 1200 0 0
Basic
Var.
Sol.
Value
X1 X2 X3 S1 S2 Min. Ratio
0 S1 160 2 4 6 * 1 0 160/6 LVC
0 S2 120 3 2 4 0 1 30
Zj 0 0 0 0 0 0
Cj – Zj 500 600 1200 0 0
EVC
Made By - Sneha Malhotra

7. Calculations for Simplex Table II
 X3 = S1
KeyValue element
S2= Old table values of S2-
[Element above or below the
key element x Value of X3 in
new table]
0
6
0
6
1
6
1
1
6
6
3
2
6
4
3
1
6
2
3
40
6
160
4120
1041
3
2
6
1
40
0144
3
2
3
2
42
3
5
3
1
43
x
x
x
x
x
x
Made By - Sneha Malhotra

8. Cj 500 600 1200 0 0
Basic
Var.
Sol.
Value
X1 X2 X3 S1 S2 Min. Ratio
1200 X3 160/6 1/3 2/3 1 1/6 0 80
0 S2 40/3 5/3* -2/3 0 -2/3 1 8 LVC
Zj 32000 400 800 1200 200 0
Cj – Zj 100 -200 0 -200 0
EVC
Made By - Sneha Malhotra

9. Calculations for Simplex Table III
 X3 = S2
KeyValue element
X3= Old table values of S2-
[Element above or below the key
element x Value of X1 in new table]
8
3
5
3
40
5
3
3
5
1
5
2
3
5
3
2
0
3
5
0
5
2
3
5
3
2
1
3
5
3
5
24
3
72
8
3
1
6
160
5
1
5
3
3
1
0
10
3
30
9
5
2
3
1
6
1
10
3
1
1
5
4
15
12
5
2
3
1
3
2
01
3
1
3
1
x
x
x
x
x
x
Made By - Sneha Malhotra

10. Cj 500 600 1200 0 0
Basic
Var.
Sol.
Value
X1 X2 X3 S1 S2
1200 X3 24 0 4/5 1 27/90 -1/5
500 X1 8 1 -2/5 0 -2/5 3/5
Zj 32800 500 760 1200 160 60
Cj – Zj 0 -160 0 -160 -60
Since all Cj- Zj are negative or zero, so we get
the optimum solution.
X1= No. of units = 8, X3 = No. of units=24
And Max. Profit Z= 500x8 + 600x0 + 1200x24
= 4000 + 0 +28800
Answer Z= Rs. 32800
Made By - Sneha Malhotra

11. ILLUSTRATION 3:
Max Z= 100X1 + 40X2
Subject to 40X1 + 50X2 ≤ 900
9X1 + 4X2 ≤ 180
Where X1 , X2 ≥ 0
ANSWER: Max Z= 100 X1 + 40X2 +0S1 +0S2
Subject to 40X1 + 50X2 +S1 +0S2= 900
9X1 + 4X2 +0S1 +S2 = 180
Where X1 , X2, S1, S2 ≥ 0
Made By - Sneha Malhotra

12. Max Z= 10X1 + 5X2
Subject to 4X1 + 5X2 ≤ 100
5X1 + 2X2 ≤ 80
Where X1 , X2 ≥ 0
ANSWER: Max Z= 10 X1 + 5X2 +0S1 +0S2
Subject to 4X1 + 5X2 +S1 +0S2= 100
5X1 + 2X2 +0S1 +S2 = 80
Where X1 , X2, S1, S2 ≥ 0
Made By - Sneha Malhotra

13. Max Z= 5X1 + 10X2 + 8X3
Subject to 3X1 + 5X2 + 2X3 ≤ 60
4X1 + 4X2 + 4X3 ≤ 72
2X1 + 4X2 + 5X3 ≤ 100
Where X1 , X2 , X3 ≥ 0
ANSWER: Max Z = 5X1 + 10X2 +8X3 +0S1 +0S2+0S3
Subject to 3X1 + 5X2 +2X3 +S1 +0S2 + 0S3= 60
4X1 + 4X2 + 4X3 +0S1 +S2 +0S3= 72
2X1 + 4X2 + 5X3 +0S1 +0S2 +S3= 100
Where X1 , X2, X3 , S1, S2 ,S3 ≥ 0
Made By - Sneha Malhotra

14. Made By - Sneha Malhotra
Cj
5 10 8 0 0 0
Basic
Variable
Solution
Value
X1 X2 X3 S1 S2 S3 Min.
Ratio
0
S1 60 3 5* 2 1 0 0 12
0
S2 72 4 4 4 0 1 0 18
0
S3 100 2 4 5 0 0 1 25
Zj 0 0 0 0 0 0 0
Cj - Zj 5 10 8 0 0 0

15. Cj
5 10 8 0 0 0
Basic
Variable
Solution
Value
X1 X2 X3 S1 S2 S3 Min.
Ratio
10
X2 12 3/5 1 2/5 1/5 0 0 30
0
S2 24 8/5 0 12/5* -4/5 1 0 10
0
S3 52 -2/5 0 17/5 -4/5 0 1 260/17
Zj 120 6 10 4 2 0 0
Cj - Zj -1 0 4 -2 0 0

16. Cj
5 10 8 0 0 0
Basic
Variable
Solution
Value
X1 X2 X3 S1 S2 S3
10 X2 8 1/3 1 0 1/3 -1/6 0
8 X3 10 2/3 0 1 -1/3 5/12 0
0 S3 18 -8/3 0 0 1/3 -17/12 1
Zj 160 26/3 10 8 2/3 5/3 0
Cj - Zj -11/3 0 0 -2/3 -5/3 0
Since all Cj – Zj ≤ 0 , so we have an optimum solution
where X1 = 0 , X2=8, X3=10
And the Max value of Z= 160.

17. Max Z= 30X1 + 40X2 + 20X3
Subject to 10X1 + 12X2 + 7X3 ≤ 10,000
7X1 + 10X2 + 8X3 ≤ 8000
X1 + X2 + X3 ≤ 1000
Where X1 , X2 , X3 ≥ 0
ANSWER: Max Z = 30X1 + 40X2 +20X3 +0S1 +0S2+0S3
Subject to 10X1 + 12X2 +7X3 +S1 +0S2 + 0S3= 10,000
7X1 + 10X2 + 8X3 +0S1 +S2 +0S3= 8000
X1 + X2 + X3 +0S1 +0S2 +S3= 1000
Where X1 , X2,X3 , S1, S2 ,S3 ≥ 0
Made By - Sneha Malhotra

18. Max Z= 3X1 + 5X2 + 4X3
Subject to 2X1 + 3X2 ≤ 8
2X2 + 5X3 ≤ 10
3X1 +2 X2 + 4X3 ≤ 15
Where X1 , X2 , X3 ≥ 0
ANSWER: Max Z = 3X1 + 5X2 +4X3 +0S1 +0S2+0S3
Subject to 2X1 + 3X2 +0X3 +S1 +0S2 + 0S3= 8
0X1 + 2X2 + 5X3 +0S1 +S2 +0S3= 10
3X1 + 2X2 + 4X3 +0S1 +0S2 +S3= 15
Where X1 , X2,X3 , S1, S2 ,S3 ≥ 0
Made By - Sneha Malhotra

19. Solve the following:
Minimize Z = 5X1 + 6X2
Subject to 2X1 + 5X2 ≥ 1500
3X1 + X2 ≥ 1200
X1 & X2 ≥ 0
SOLUTION: Introduction surplus variables S1 & S2 with
zero coefficient and artificial variables A1 & A2 with the “M”
coefficient, the objective function and the constrains will be
as follows:
Minimize Z= 5X1 + 6X2 +0S1 + MA1 + MA2
Subject to 2X1 + 5X2 – S1 + 0S2 + A1 + 0A2 = 1500
3X1 + X2 + 0S1 – S2 + 0A1 + A2 = 1200
When X1,X2,S1,S2,A1,A2 ≥ 0
Made By - Sneha Malhotra

20. Cj 5 6 0 0 M M
Basic
Variable
Solution
Value
X1 X2 S1 S2 A1 A2
Min.
Ratio
M A1 1500 2 5* -1 0 1 0
300
LVC
M A2 1200 3 1 0 -1 0 1 1200
Zj 2700M 5M 6M -M -M M M
Cj - Zj 5-5M 6-6M M M 0 0
EVC
Made By - Sneha Malhotra

21. Calculations for Simplex Table II
 X2 = A1
KeyValue element
A2= Old table values of A2-
[Element above or below the
key element x Value of X2 in
new table]
0
5
0
0
5
0
5
1
5
1
1
5
5
5
2
5
2
300
5
1500
1011
1011
5
1
5
1
10
0111
5
13
5
2
13
90030011200
x
x
x
x
x
x
Made By - Sneha Malhotra

22. Cj 5 6 0 0 M M
Basic
Var.
Sol.
Value
X1 X2 S1 S2 A1 A2 Min.
Ratio
6 X2 300 2/5 1 -1/5 0 - 0 750
M A2 900 13/5* 0 1/5 -1 - 1
4500
----------
13
Zj
1800+
900M
12+13M
--------
5
6
-6+M
----------
5
-M - M
Cj - Zj
13-13M
----------
5
0
6-M
----------
5
M - 0
EVC
LVC
Made By - Sneha Malhotra

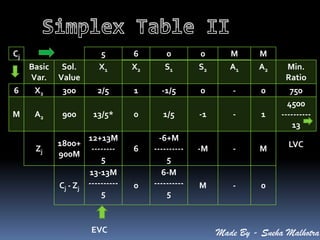
23. Calculations for Simplex Table III
 X1 = A2
KeyValue element
X2= Old table values of X2-
[Element above or below the key
element x Value of X1 in new table]
13
5
13
5
1
13
1
13
5
5
1
0
13
5
0
1
13
5
5
13
13
4500
13
5
900
x
x
x
x
x
13
2
13
5
5
2
0
13
3
13
1
5
2
5
1
10
5
2
1
01
5
2
5
2
13
2100
13
4500
5
2
300
x
x
x
x
x

24. Cj 5 6 0 0
Basic
Values
Solution
Values
X1 X2 S1 S2
6 X2 2100/13 0 1 -3/13 2/13
5 X1 4500/13 1 0 1/13 -5/13
Zj 2700 5 6 -1 -1
Cj - Zj 0 0 1 1
Since all the elements in Cj-Zj are positive, the optimal solution is
obtained.
2700
23.96977.1730
13
12600
13
22500
13
2100
6
13
4500
5
13
2100
,
13
4500
21
RsZMin
ZMinimum
XX
Made By - Sneha Malhotra

25. Min Z= 60X1 + 80X2
Subject to 20X1 + 30X2 ≤ 900
40X2 + 30X3 ≤ 1200
Where X1 , X2 ≥ 0
ANSWER:MinZ =60X1 + 80X2 +0S1 +0S2+MA1+ MA2
Subject to 20X1 + 30X2 -S1 +A1= 900
40X1 + 30X2 +0S1 -S2 +A2= 1200
Where X1 , X2 ,S1, S2 ,A1 ,A2≥ 0
Made By - Sneha Malhotra

26. Min Z= 4X1 + 6X2
Subject to X1 + 2X2 ≥80
3X1 + X2 ≥ 75
Where X1 , X2 ≥ 0
ANSWER: Min Z = 4X1 + 6X2 +0S1 +0S2+MA1+ MA2
Subject to X1 + 2X2 -S1 +0S2 +A1 +0A2= 80
3X1 + X2 +0S1 -S2 +0A1 +A2= 75
Where X1 , X2 ,S1, S2 ,A1 ,A2≥ 0
Made By - Sneha Malhotra

27. Made By - Sneha Malhotra