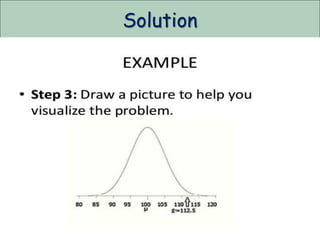
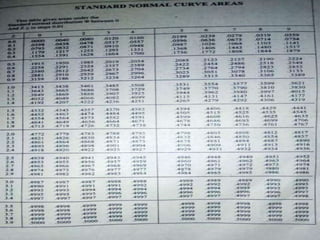
The document discusses the z-test, a statistical procedure used to test the difference between two population means. It provides the formulas and steps to conduct a z-test, including stating the null and alternative hypotheses, finding the z-score, and interpreting the results. An example problem is shown where a z-test is used to determine if the mean IQ scores of students at a school are above average. A second example tests if the mean concentration of a trace element is the same between male and female blood donors.

1. Z- TEST
CHERYL M. ASIA
DISCUSSANT
DEAN MELCHOR JULLANES
PROFESSOR
SEPTEMBER 8, 2019

2. Z-TEST
Z-Test is a statistical procedure used to test an
alternative hypothesis against null hypothesis.
Z-Test is any statistical hypothesis used to determine
whether tow samples’ means are different when the
variances are known and sample is large (n ≥ 30 ).
Z- Test is a comparison of the means of two
independent group samples, taken from one
populations with known variance.

3. Null Hypothesis vs.
Alternative Hypothesis
The null hypothesis ( H0 ) is a hypothesis which a
researcher tries to disprove, reject or nullify.The refers
often to the common view of something;
While, the alternative hypothesis ( Ha ) is what the
researcher really thinks in the cause of a phenomenon.

4. Z- Test Formula

5. Z- Test is used…
 When samples are drawn from random.
When the samples are taken from population are
independent.
When standard deviation is known.
When the number of population is large (n ≥ 30 ).

6. Large Sample is used…
When we perform the statistical test we are trying to
judge the validity of the null hypothesis.We are
doing so with an incomplete view of population. Our
sample is our window into the population.The larger
the sample size the bigger the window. However
without the full view of population there is always
the chance that our sample will lead us to wrong
conclusion.

7. Problem
• A principal at Maria Clara High school claims that the
students in the school are above average
intelligence.
• A random sample of 30 students’ IQ scores have the
mean score of 112. 5. Is there sufficient evidence to
support the principal’s claim?
• The mean population IQ is 100 with standard
deviation of 15.

8. Solution
Step 1:
• State the Null Hypothesis
The accepted fact that the population mean is 100,
so the H0: µ = 100
Step 2:
• State the Alternative Hypothesis
The claim is the students have the above average IQ
scores , so Ha: µ > 100

9. Solution

10. Solution
Step 4
• State the Alpha Level, if you aren’t given the
formula for the alpha level, use 0.05, an
alpha level of 0.05 is equal to the z- score of
is equal to the z- score of 1. 645.
( to calculate the z- score you can useTI-83
calculator)

11. Solution
Step 5:
find the Z using the formula:
For this set of data:
(112,5 – 100) / (15/ √ 30) = 4.56

12. Solution
Step 6:Interpret the result
If step 5 result is (4.56) is greater than step 4
( 1.645) , reject the null hypothesis. If it’s less
than step 4, you cannot reject the
hypothesis. In this case it is greater, so you
can reject the null and principals claim is
right.

14. Z-Test for TWO SAMPLES
• Requirements
Two normally distributed but independent
populations, Ợ is known
Formula:
Where: X1 and X2 are the means of two samples
µ1 - µ2 , hypothesized difference between the
population mean
Ợ1 and Ợ2 are the standard deviation of two
population
n1 and n2 are the size of the two samples

15. Z-Test for Two Sample
Problem
• The amount of certain trace element in blood is
known to vary with the standard deviation of 14.1
ppm ( parts per million) for male blood donors, and
9.5 ppm for female donors.
• Random samples of 75 male and 50 female yield
concentration means of 28 and 33 ppm respectively.
What is the likelihood of populations means of
concentration of the element are the same for men
and women?

16. Z- test for Two Sample
Requirements
Two normally distributed but independent
populations, Ợ is known
Formula:
Null Hypothesis:
H0 = µ1 = µ2
or Ho = µ1 - µ2 = 0
Alternative Hypothesis:
Ha = µ1 ≠ µ2
or Ha = µ1 - µ2 ≠0

17. SolutionGiven:
X1 = 26 , mean for male
X2 = 33 , mean for female
Ợ1 = 14.1 , SD for male
Ợ2 = 9.5 , SD for female
n1 = 75 , sample size for male
And n2 = 50, sample size for female
Substituting the value:

18. Interpretation
• The computed Z- value is negative because the
mean of female was subtracted from the mean of
males.
• But the order of the samples in this computation is
arbitrary – it could be in opposite order, in which
case z will be 2.37 instead of – 2.37. an extreme z-
score from alpha level ( which is 5% = + 1.654 or
– 1.654) will lead to rejection to the null hypothesis.