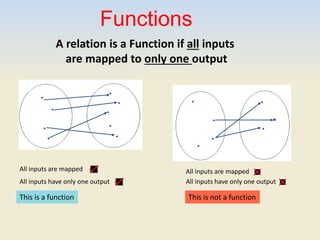
1. A relation is a rule that links one or more inputs to one or more outputs. A relation is a function if each input is mapped to only one output. 2. Functions can be represented graphically using graphs or arrow charts, or non-graphically using sets of ordered pairs. Common functions include those that map states to capitals or people to grandparents. 3. For a function to be injective, no two inputs can map to the same output. To be surjective, every element in the codomain must have some input mapped to it. A function is bijective if it is both injective and surjective.

1. Relations
A Relation is a rule that links
one or more
output to one or more input
An input is an
element in the starter
set.
It can also be called x
value
An output is an
element in the arrival
set.
It can also be called y
value
Inputs Outputs

2. Functions
A relation is a Function if all inputs
are mapped to only one output
This is a function
All inputs are mapped
All inputs have only one output
All inputs are mapped
All inputs have only one output
This is not a function

3. For example…
State Capital
New Jersey Trenton
New York Albany
Colorado Denver
Rhode Island Providence
Person Grandparent
Eric Arthur
Eric Ellie
Maria Camine
Maria Susan
This tab, where each state is
mapped with its capital,
represents a function, because
every state (inputs) has only one
capital (outputs).
This tab instead, that maps every
person with his grandparents, isn’t
a function, because they both have
two grandparents (outputs).

4. x y
5 7
2 9
0 8
-4 6
x y
4 3
2 8
0 8
4 6
Here, each number in the x
(inputs) column has only one
y (output) as an answer, so it
is a function.
Here, the input 4 has an
output of both 3 and 6, so it
can’t be a function.

5. How to represent a function
A function can be represented in three ways:
1-the graph
2-the arrow chart
3-the set of ordered pairs

6. The graph
The graph of a function is a
cartesian coordinate system
where the couples of x and y
values are represented.
this is an example
of the graph of the
function:
y=2x+6

7. The arrow chart
The arrow chart of a function is another graphical representation
The arrows show how the numbers in the domain are mapped into numbers in the
range and represent the function f: y=f(x)

8. The set of ordered pairs
a set of ordered pairs is a non-graphical way to represent a function;
the couples of x and y values will be represented as shown in the following
way:
y=2x+6----> {(1,8),(2,10),(3,12)}
X Y
1 3
2 10
3 12

9. 1 Is the following a function?
Yes
No
1
2
3
4
5
4
3
2
A
B

10. 1 Is the following a function?
1
2
3
4
5
4
3
2
Because each input is mapped into only one output
Correct!!

11. 1
1
2
3
4
5
4
3
2
Is the following a function?
Wrong!
It is a function because each input is mapped into only one output

12. 2 Is the following a function?
City State
Englewood New Jersey
Englewood Colorado
Springfield Maryland
Springfield Illinois
Springfield Montana
Yes
No
A
B

13. 2 Is the following a function?
City State
Englewood New Jersey
Englewood Colorado
Springfield Maryland
Springfield Illinois
Springfield Montana
Correct!!!

14. 2 Is the following a function?
City State
Englewood New Jersey
Englewood Colorado
Springfield Maryland
Springfield Illinois
Springfield Montana
Wrong!

15. Vertical Line Test: if every vertical line you can
draw goes through only 1 point then the relation is a
function.

16. Function Function Not a function
Example

17. Not a function
This isn’t a function
because
the vertical line goes
through
two points.

18. Is this a function?
Yes
No
A
B

19. Is this a function?
Correct!!!

20. Is this a function?
Wrong!

21. Is this a function?
Yes
No
A
B

22. Is this a function?
Correct!!!

23. Is this a function?
Wrong!

24. Is this a function?
Yes
No
A
B

25. Is this a function?
Correct!!!

26. Is this a function?
Wrong!

27. Domain codomain and
range

28. Any set of numbers that is the input of a
relation or function is called the domain.
Any set of numbers that is the output of a
relation or function is called the range.
Domain: {1, 2, 3, 4} Range: {42,
98, 106, 125}

29. f(x) Y=2x+1
3
2
DOMAIN: a set of first element
in a relation ( all of the x values ).
These are also called the
independent variable.
RANGE:the second and actuals
elements in a relation ( all of the
y values ). These are also called
the dependent variable
1
3
4
5
7
9
CODOMAIN: is the set of all possible and second elements in a
relation.

30. • Domain = {Joe, Mike,
Rose, Kiki}
• Range = {6, 5.75, 5,
6.5}
Example
Joe
Mike
Rose
kiki
DOMAIN RANGE
6
5,75
5
6,75

31. Domain (set of all x’s) Range (set of all y’s)
1
2
3
4
5
2
10
8
6
4

32. Which numbers are in the domain?
2
4
6
8
10
10
20
30
40
50
2
10
12
8
20
A
B
C
D
E

33. Which numbers are in the domain?
2
4
6
8
10
10
20
30
40
50
2
10
8
A
B
D

34. Which numbers are in the range?
2
4
6
8
10
10
20
30
40
50
2
10
12
8
20
A
B
C
D
E

35. Which numbers are in the range?
2
4
6
8
10
10
20
30
40
50
10
20
B
E

36. Which numbers are part of the domain?
{(24, 12), (22, 11), (20, 10), (18, 9)}
12
20
24
11
9
A
B
C
D
E

37. Which numbers are part of the domain?
{(24, 12), (22, 11), (20, 10), (18, 9)}
20
24
B
C

38. Which numbers are part of the range?
{(24, 12), (22, 11), (20, 10), (18, 9)}
12
20
24
11
9
A
B
C
D
E

39. Which numbers are part of the range?
{(24, 12), (22, 11), (20, 10), (18, 9)}
12
11
9
A
D
E

40. INJECTIVE, SURJECTIVE and
BIJECTIVE FUNCTIONS.

41. •
•
•
• •
•
• •
X
Y
Let f be a function whose domain is a set X.
The function f is injective if for all a and b in X, if f(a)
= f(b) then a = b; Equivalently, if a ≠ b, then f(a) ≠ f(b).
So….
F(x) is injective (also called one-to-one) if no two
inputs have the same output.

42. This is an INJECTIVE function.
This isn’t an INJECTIVE
function because we can
see that two different
elements ‘3;4’ in the
domain have the same
output ‘C’.

43. To be a one-to-one function, each y value could only be
paired with one x. Let’s look at a couple of graphs.
Look at a y value (for example
y = 3) and see if there is only
one x value on the graph for it.
This is NOT a one-to-one
function
For any y value, a horizontal line
will only intersect the graph once
so will only have one x value
This then IS a one-to-one
function

44. If a horizontal line intersects the graph of an
equation more than one time, the equation
graphed is NOT a one-to-one function.
This is an injective
funtion.
This is NOT an
injective funtion.
This is NOT an
injective funtion.

45. •
•
• •
•
•
•
X
Y
A function f (from set X to Y) is surjective if and only if for
every b in Y, there is at least one a in X.
So…
A function is surjective (onto) if every element in the
codomain (Y) has some element from the domain (X) mapped
on to it.
In other words: f(x) is surjective when the range is equal to
the codomain.

46. It’s surjective because all
elements in the codomain
has an input
It isn’t surjective because
there is an element in the
codomain Y that hasn’t an
input

47. •
•
•
•
•
•
A
B
A function f (from set A to B) is bijective if, for
every y in B, there is exactly one x in A such that
f(x) = y .
So…
A function is bijective if it’s both injective and
surjective.
•Is injective because each input has a
different output.
•is surjective because the range is all
codomain.
It’s BIJECTIVE

48. a
b
c
1
2
This function is:
•injective
•surjective
•bijective
•neither
a
b
c
1
2
3
This function is:
•injective
•surjective
•bijective
•neither

49. Davide
Lia
Ugo
Irene
Marco
Erika
This function is:
•injective
•surjective
•bijective
•neither
Tom
Gigi
Carla
Sammy
Anna
This function is:
•injective
•surjective
•bijective
•neither

50. A: {Maria; Francesca; Vanessa; Gaia}
B: {Edoardo; Andrea; Luca; Davide}
A B
Maria Andrea
Vanessa Edoardo
Francesca Luca
Gaia Davide
This is a function:
•Injective
•Surjective
•Bijective

51. A: {Maria; Vanessa; Gaia}
B: {Edoardo; Andrea; Luca; Davide}
A B
Maria Andrea
Vanessa Edoardo
Gaia Davide
This is a function:
•Injective
•Surjective
•Bijective

52. A: {Maria; Francesca; Vanessa; Gaia; Ilaria}
B: {Edoardo; Andrea; Luca; Davide}
A B
Maria Andrea
Vanessa Edoardo
Francesca Luca
Gaia Edoardo
Ilaria Davide
This is a function:
•Injective
•Surjective
•Bijective