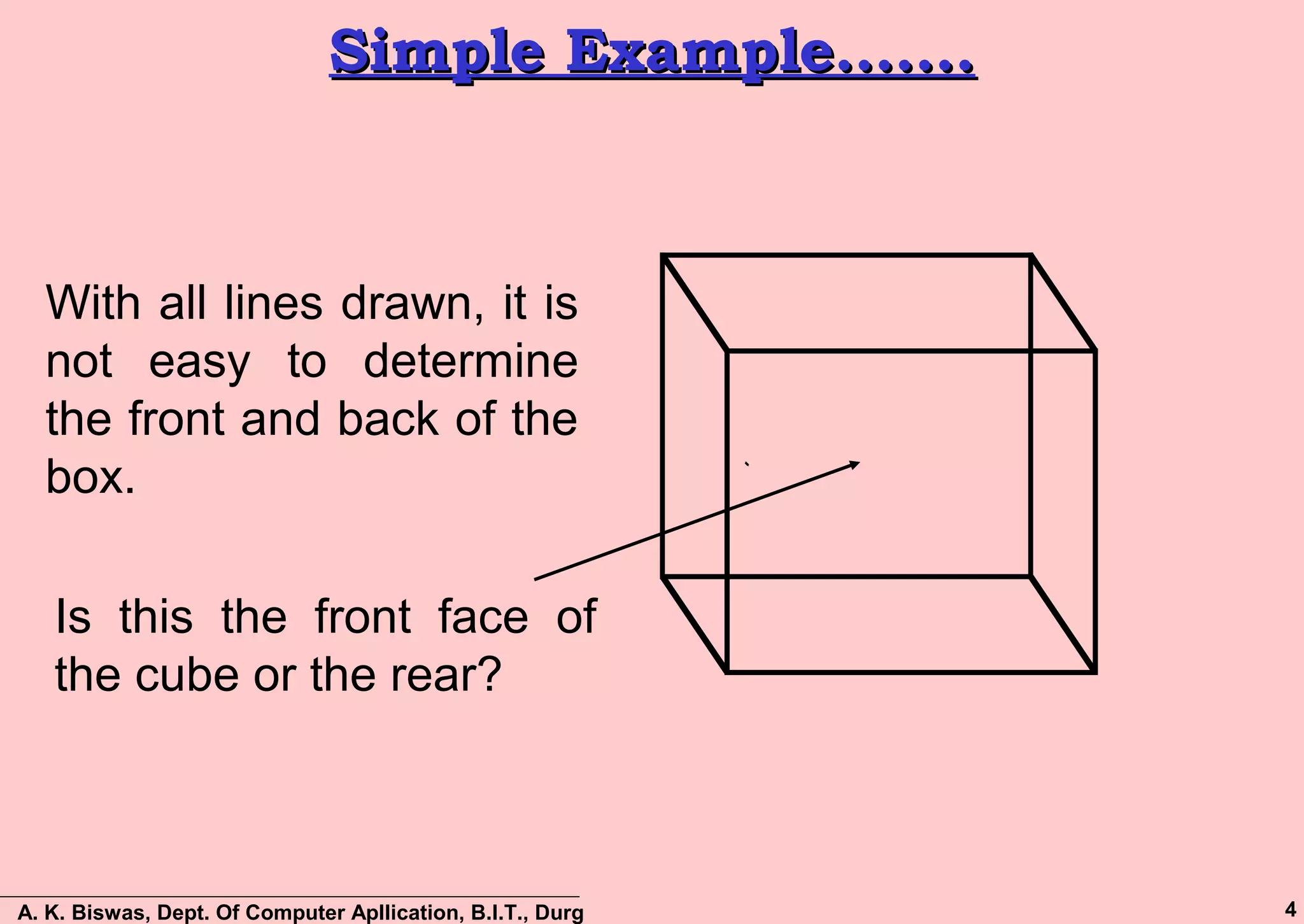
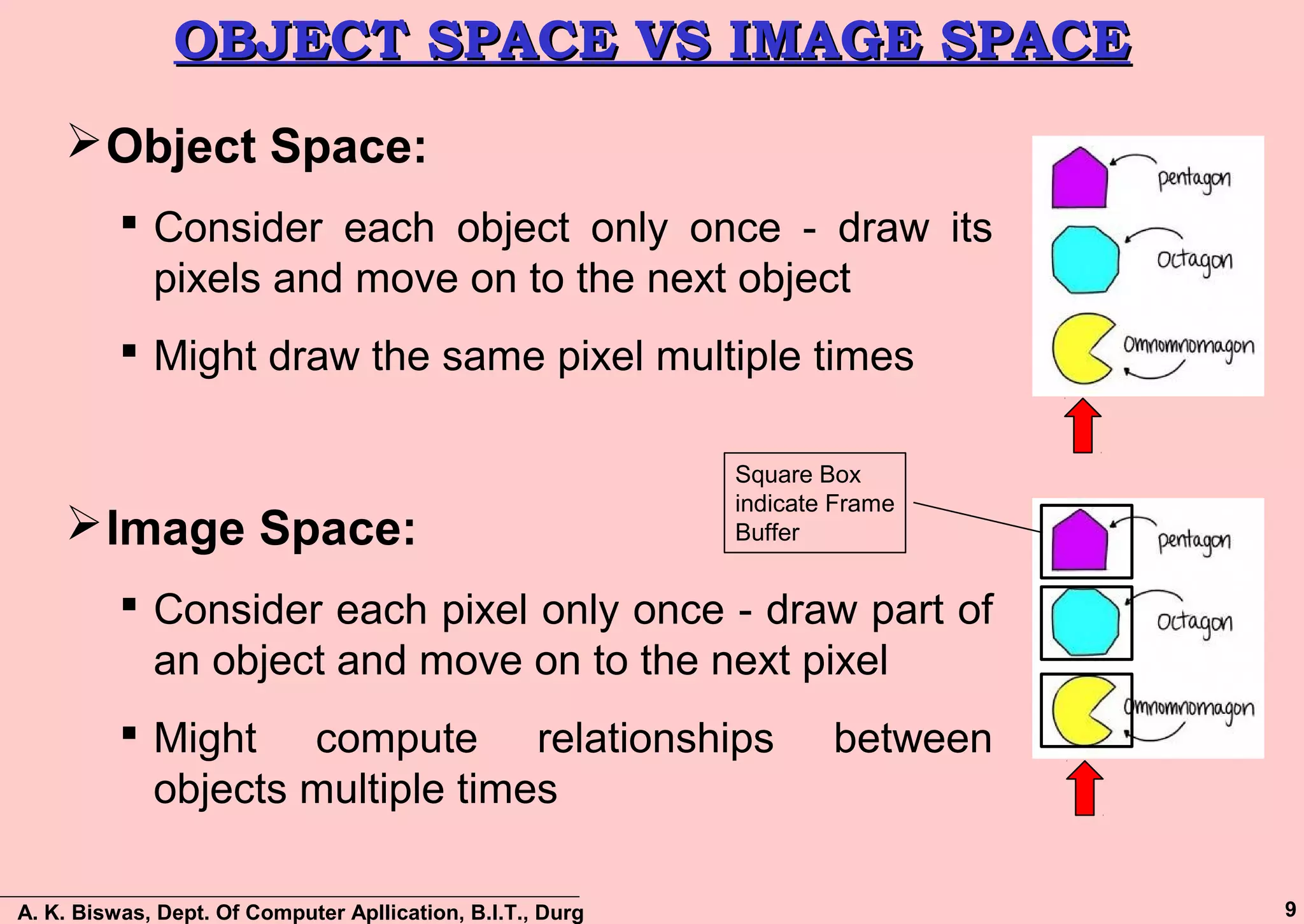
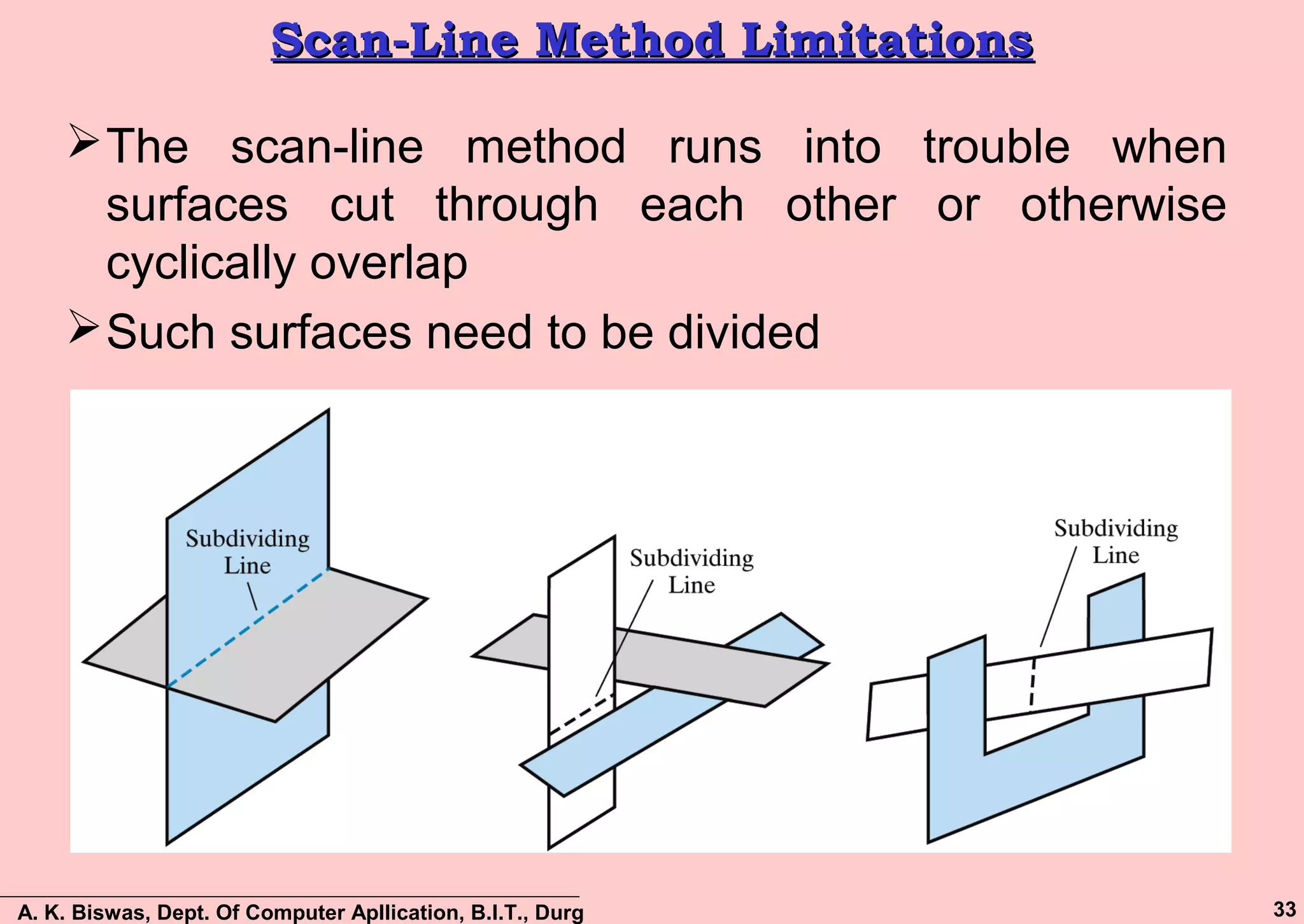
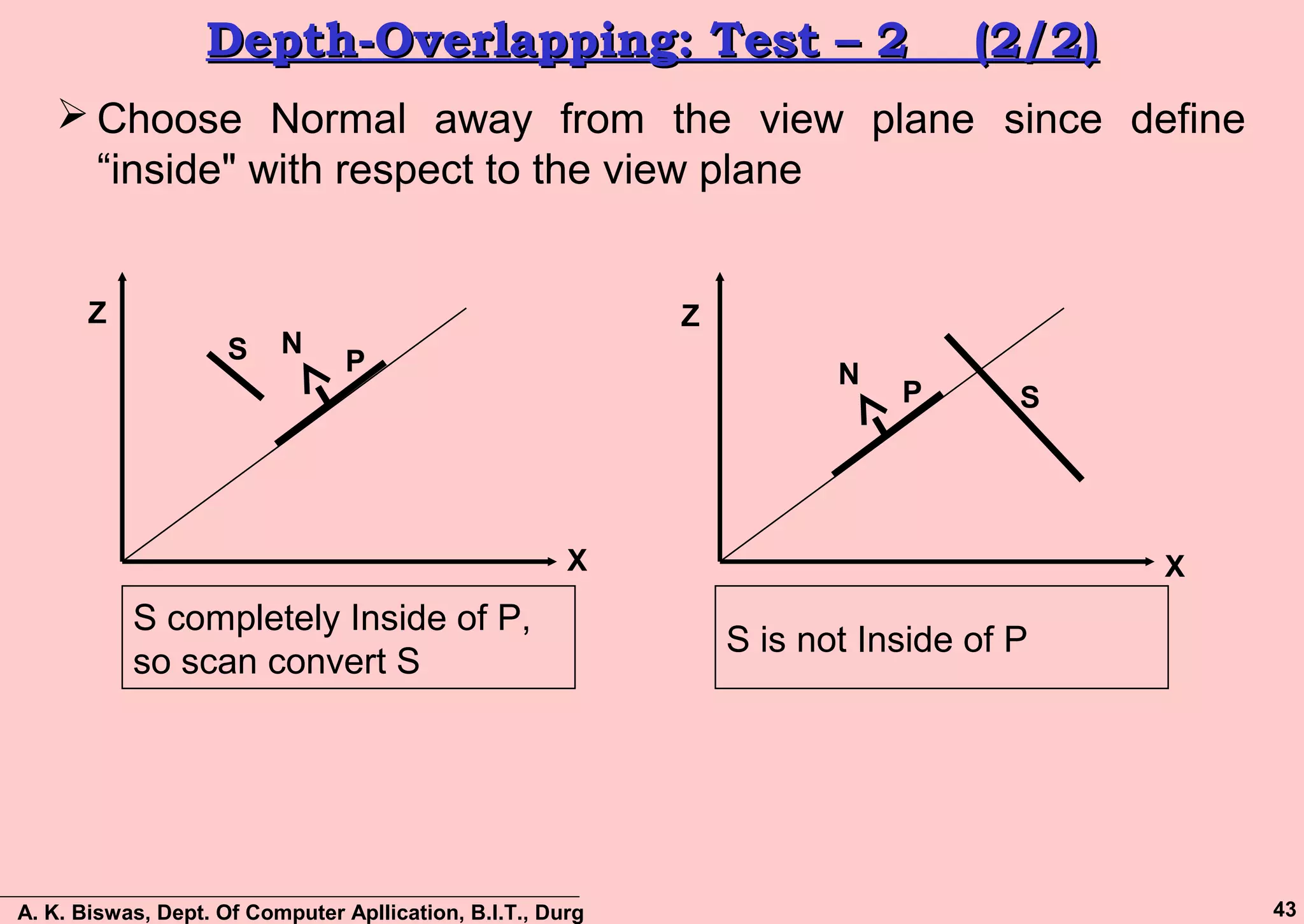
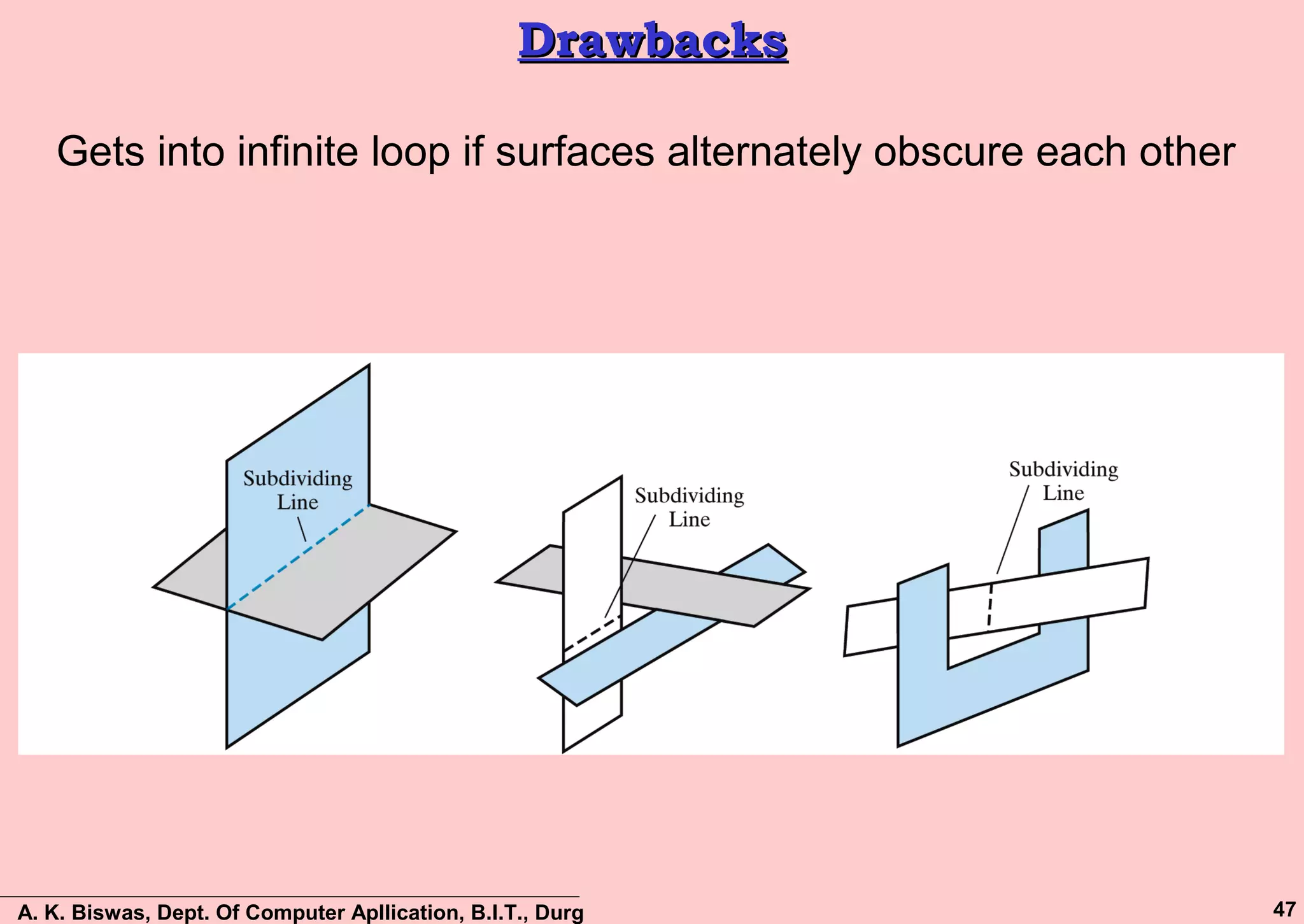
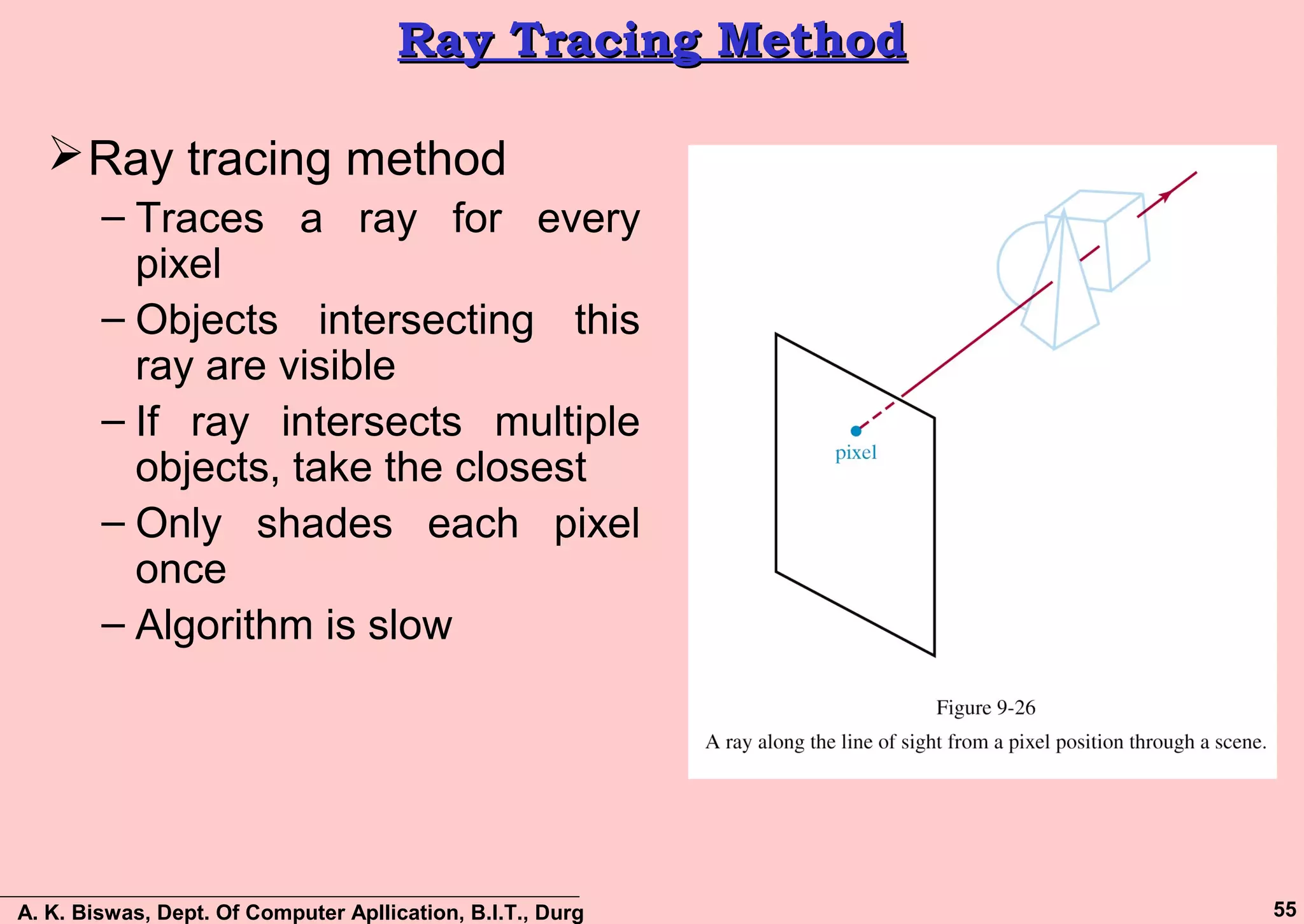
The document discusses various methods for visible surface detection and hidden surface elimination in computer graphics, focusing on approaches like back-face detection, depth-buffer, a-buffer, scan-line method, and depth-sorting. It emphasizes the importance of determining which surfaces are visible from a particular viewpoint to optimize rendering and reduce unnecessary calculations. The document also outlines the benefits and limitations of each method, providing insights into their computational processes and applications.