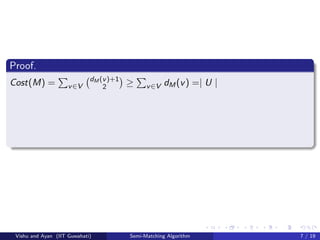
This document summarizes a paper that presents a distributed 2-approximation algorithm for the semi-matching problem. The algorithm aims to match clients (set U) to servers (set V) in a bipartite graph G=(V,U,E). It finds a non-swappable semi-matching M that is a (1+1/α)-approximation of the optimal semi-matching M* in O(Δ5) steps, where Δ is the maximum degree of V. It works by systematically eliminating bad paths from an initial semi-matching M through swapping operations until no bad paths remain.

1. Distributed 2-Approximation Algorithm for the
Semi-Matching Problem
Paper by
A Czygrinow, M Han´ckowiak, E Szyma´nska, W Wawrzyniak
Presentation by
Vishu & Ayan Sengupta
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 1 / 19

2. Introduction
We consider the problem of matching clients with servers.
Also known as Load Balancing Problem.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 2 / 19

3. Introduction
We consider the problem of matching clients with servers.
Also known as Load Balancing Problem.
We will consider bipartite graphs, G = (V , U, E) with the disjoint set of
vertices V and U such that degree of every vertex in U is atleast 1 and E
is the edge relations between them.
∆ is the maximum degree of vertices in V .
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 2 / 19

4. Introduction
We consider the problem of matching clients with servers.
Also known as Load Balancing Problem.
We will consider bipartite graphs, G = (V , U, E) with the disjoint set of
vertices V and U such that degree of every vertex in U is atleast 1 and E
is the edge relations between them.
∆ is the maximum degree of vertices in V .
Here, U is the set of clients, V is the set of servers and E is the set of
available connection between them.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 2 / 19

5. Introduction
We consider the problem of matching clients with servers.
Also known as Load Balancing Problem.
We will consider bipartite graphs, G = (V , U, E) with the disjoint set of
vertices V and U such that degree of every vertex in U is atleast 1 and E
is the edge relations between them.
∆ is the maximum degree of vertices in V .
Here, U is the set of clients, V is the set of servers and E is the set of
available connection between them.
Our goal is to find a set of edges M ⊆ E such that every vertex in U is
incident with exactly one edge in M such that sum of the loads of the
servers (we define as cost(M)) is minimized.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 2 / 19

6. Definitions
A Semi-matching in a bipartite graph G = (V , U, E) is a set of
edges M ⊆ E such that every vertex u ∈ U is incident with exactly
one edge in M.
dM(v) is the Degree of vertex v in the semi-matching M.
The total completion time of a server v ∈ V for its dM(v) clients is
1 + 2 + ... + dM(v) = dM (v)+1
2 .
The cost of the semi-matching M, cost(M) is v∈V
dM (v)+1
2 .
A semi-matching M is non-swappable if for all v, w ∈ V and u ∈ U,
such that vu ∈ M and uw ∈ E M it holds that dM(v) ≤ dM(w) + 1.
A path P = vuw is called a bad path, if dM(v) ≥ dM(w) + 2.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 3 / 19

7. Definitions
For any A, B ⊂ V , we define Bad(A, B) to be the set of all bad paths
xuy such that x ∈ A, u ∈ U and y ∈ B.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 4 / 19

8. Definitions
For any A, B ⊂ V , we define Bad(A, B) to be the set of all bad paths
xuy such that x ∈ A, u ∈ U and y ∈ B.
Note : Bad(V , V ) = φ with respect to a semi-matching implies that
the semi-matching is non-swappable.
We further define Badind (A, B) to be the maximal set of paths from
Bad(A, B) such that for any two paths P, P ∈ Badind (A, B),
Start(P) ∩ Start(P ) = φ and End(P) ∩ End(P ) = φ.
If M is a semi-matching and Z is a set of bad paths then Z M
(same as M Z) is the semi-matching obtaining from M by deleting
the edge vu ∈ M and adding uw for every path vuw ∈ Z. (We often
call this process ”swapping”)
For a semi-matching M, Vk = {v ∈ V |dM(v) = k}.
Similarly, V≤k = {v ∈ V |dM(v) ≤ k}, V<k, V>k and V≥k.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 4 / 19

9. Sketch of Algorithm
We take our message passing model to be synchronous.
Our goal is to get a non-swappable semi-matching M from an optimal
semi-matching M∗, which is (1 + 1
α)-approximation of M∗.
Step 1 : Starts by finding an arbitrary semi-matching M.
Step 2 : Systematically eliminate the bad paths by swapping operation.
Step 3 : Again eliminate bad paths from the newly formed
semi-matching.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 5 / 19

10. Sketch of Algorithm
We take our message passing model to be synchronous.
Our goal is to get a non-swappable semi-matching M from an optimal
semi-matching M∗, which is (1 + 1
α)-approximation of M∗.
Step 1 : Starts by finding an arbitrary semi-matching M.
Step 2 : Systematically eliminate the bad paths by swapping operation.
Step 3 : Again eliminate bad paths from the newly formed
semi-matching.
This process will terminate after finite iterations. We will show that our
algorithm returns a non-swappable semi-matching in O(∆5) steps, where
∆ = maxv∈V dE (v).
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 5 / 19

11. Theorem (1)
For any non-swappable semi-matching M in G = (V , U, E),
Cost(M) ≤ (1 + 1
α )Cost(M∗), where α = max{1, 1
2(|U|
|V | + 1)}
Proof: In order to prove this theorem we need the following result.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 6 / 19

12. Theorem (1)
For any non-swappable semi-matching M in G = (V , U, E),
Cost(M) ≤ (1 + 1
α )Cost(M∗), where α = max{1, 1
2(|U|
|V | + 1)}
Proof: In order to prove this theorem we need the following result.
Fact : For any semi-matching M in G = (U, V , E) it holds
Cost(M) ≥ α | U |, where α = max{1, 1
2(|U|
|V | + 1)}
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 6 / 19

13. Proof.
Cost(M) = v∈V
dM (v)+1
2 ≥ v∈V dM(v) =| U |
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 7 / 19

14. Proof.
Cost(M) = v∈V
dM (v)+1
2 ≥ v∈V dM(v) =| U |
as well as, by Cauchy- Schwartz inequality
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 7 / 19

15. Proof.
Cost(M) = v∈V
dM (v)+1
2 ≥ v∈V dM(v) =| U |
as well as, by Cauchy- Schwartz inequality
Cost(M) = v∈V
dM (v)+1
2
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 7 / 19

16. Proof.
Cost(M) = v∈V
dM (v)+1
2 ≥ v∈V dM(v) =| U |
as well as, by Cauchy- Schwartz inequality
Cost(M) = v∈V
dM (v)+1
2 ≥| V |
v∈V dM (v)
|V |
+1
2
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 7 / 19

17. Proof.
Cost(M) = v∈V
dM (v)+1
2 ≥ v∈V dM(v) =| U |
as well as, by Cauchy- Schwartz inequality
Cost(M) = v∈V
dM (v)+1
2 ≥| V |
v∈V dM (v)
|V |
+1
2
= 1
2 | U | (|U|
|V | + 1)
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 7 / 19

18. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

19. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

20. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Define an auxiliary multi-diagraph D such that for any u ∈ U there is an
arc (vu, v∗
u ) ∈ D if vu = v∗
u .
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

21. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Define an auxiliary multi-diagraph D such that for any u ∈ U there is an
arc (vu, v∗
u ) ∈ D if vu = v∗
u .
We assume that D is connected, as otherwise we could analyze each
component seperately (note that cost(M) is additive).
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

22. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Define an auxiliary multi-diagraph D such that for any u ∈ U there is an
arc (vu, v∗
u ) ∈ D if vu = v∗
u .
We assume that D is connected, as otherwise we could analyze each
component seperately (note that cost(M) is additive).
Let d+
D (v), d−
D (v) denote the out-degree and the in-degree of vertex v
respectively.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

23. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Define an auxiliary multi-diagraph D such that for any u ∈ U there is an
arc (vu, v∗
u ) ∈ D if vu = v∗
u .
We assume that D is connected, as otherwise we could analyze each
component seperately (note that cost(M) is additive).
Let d+
D (v), d−
D (v) denote the out-degree and the in-degree of vertex v
respectively.
Consider two subsets of V.
V + = {v ∈ V : d+
D (v) > d−
D (v)},
V− = {v ∈ V : d−
D (v) > d+
D (v)}.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

24. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Define an auxiliary multi-diagraph D such that for any u ∈ U there is an
arc (vu, v∗
u ) ∈ D if vu = v∗
u .
We assume that D is connected, as otherwise we could analyze each
component seperately (note that cost(M) is additive).
Let d+
D (v), d−
D (v) denote the out-degree and the in-degree of vertex v
respectively.
Consider two subsets of V.
V + = {v ∈ V : d+
D (v) > d−
D (v)},
V− = {v ∈ V : d−
D (v) > d+
D (v)}.
Let d = v∈V+
(d+(v) − d−(v)) = v∈V−
(d−(v) − d+(v)).
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

25. Proof of Theorem 1.
Let M be a non-swappable semi-matching and let M∗ be an optimal
semi-matching in G.
For any u ∈ U set vu, v∗
u in such a way that uvu ∈ M and uv∗
u ∈ M∗.
Define an auxiliary multi-diagraph D such that for any u ∈ U there is an
arc (vu, v∗
u ) ∈ D if vu = v∗
u .
We assume that D is connected, as otherwise we could analyze each
component seperately (note that cost(M) is additive).
Let d+
D (v), d−
D (v) denote the out-degree and the in-degree of vertex v
respectively.
Consider two subsets of V.
V + = {v ∈ V : d+
D (v) > d−
D (v)},
V− = {v ∈ V : d−
D (v) > d+
D (v)}.
Let d = v∈V+
(d+(v) − d−(v)) = v∈V−
(d−(v) − d+(v)).
Clearly, if V+ = V− = φ then cost(M)cost(M∗). In the other case we use
the following theorem about an Eulerian cover by arc-disjoint open
trials.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 8 / 19

26. Theorem
For every connected directed multigraph D with d > 0 there exist(edge
disjoint) open trials P1, P2, ..., Pd which cover D ,i.e. D = d
j=1 Pj and
Pi Pj = φ(edgewise), where the beginnings of P1, P2, ..., Pd are in V +,
while the ends are in V −.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 9 / 19

27. Theorem
For every connected directed multigraph D with d > 0 there exist(edge
disjoint) open trials P1, P2, ..., Pd which cover D ,i.e. D = d
j=1 Pj and
Pi Pj = φ(edgewise), where the beginnings of P1, P2, ..., Pd are in V +,
while the ends are in V −.
Using the above theorem and the above fact, we obtain
cost(M) ≤ cost(M∗)+ | D |≤ (1 + 1
α )cost(M∗).
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 9 / 19

28. Theorem
For every connected directed multigraph D with d > 0 there exist(edge
disjoint) open trials P1, P2, ..., Pd which cover D ,i.e. D = d
j=1 Pj and
Pi Pj = φ(edgewise), where the beginnings of P1, P2, ..., Pd are in V +,
while the ends are in V −.
Using the above theorem and the above fact, we obtain
cost(M) ≤ cost(M∗)+ | D |≤ (1 + 1
α )cost(M∗).
For, arbitrary, non-swappable semi-matching the above theorem yields the
following.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 9 / 19

29. Theorem
For every connected directed multigraph D with d > 0 there exist(edge
disjoint) open trials P1, P2, ..., Pd which cover D ,i.e. D = d
j=1 Pj and
Pi Pj = φ(edgewise), where the beginnings of P1, P2, ..., Pd are in V +,
while the ends are in V −.
Using the above theorem and the above fact, we obtain
cost(M) ≤ cost(M∗)+ | D |≤ (1 + 1
α )cost(M∗).
For, arbitrary, non-swappable semi-matching the above theorem yields the
following.
Corollary 1 : For any non-swappable semi-matching M in G,
cost(M) ≤ 2.cost(M∗).
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 9 / 19

30. SemiMatch Algorithm
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 10 / 19

31. Analysis of Algorithm
Some important facts :
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 11 / 19

32. Analysis of Algorithm
Some important facts :
1. If dM(v) ≥ k + 2, then − 1 ≤ d
(j)
M (v) − dM(v) ≤ 0.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 11 / 19

33. Analysis of Algorithm
Some important facts :
1. If dM(v) ≥ k + 2, then − 1 ≤ d
(j)
M (v) − dM(v) ≤ 0.
2. If dM(v) = k + 1, then d
(j)
M (v) − dM(v) = 0.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 11 / 19

34. Analysis of Algorithm
Some important facts :
1. If dM(v) ≥ k + 2, then − 1 ≤ d
(j)
M (v) − dM(v) ≤ 0.
2. If dM(v) = k + 1, then d
(j)
M (v) − dM(v) = 0.
3. If dM(v) ≤ k, then 0 ≤ d
(j)
M (v) − dM(v) ≤ 1.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 11 / 19

35. Analysis of Algorithm
Some important facts :
1. If dM(v) ≥ k + 2, then − 1 ≤ d
(j)
M (v) − dM(v) ≤ 0.
2. If dM(v) = k + 1, then d
(j)
M (v) − dM(v) = 0.
3. If dM(v) ≤ k, then 0 ≤ d
(j)
M (v) − dM(v) ≤ 1.
4. For every k and i, if Bad(V , V<k) = φ at the beginning of the i-th
iteration (step 3), then Bad(V , V<k) = φ after this iteration.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 11 / 19

36. Analysis of Algorithm
5. Let Bad(V , V<k−1) = φ at the beginning of the k-th iteration (step 2)
for some k. Then for every i ∈ {0, ...2∆} and every v ∈ Vk after steps
4 − 12 of the i-th iteration at least one of the following conditions is
satisfied :
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 12 / 19

37. Analysis of Algorithm
5. Let Bad(V , V<k−1) = φ at the beginning of the k-th iteration (step 2)
for some k. Then for every i ∈ {0, ...2∆} and every v ∈ Vk after steps
4 − 12 of the i-th iteration at least one of the following conditions is
satisfied :
a) Bad(V , v) = φ.
b) | Bad(V , v) | decreases by at least one in the i-th iteration.
c) max{dM(w) | w ∈ Starts(Bad(V , v))} decreases by at least one in
the i-th iteration.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 12 / 19

38. 6. Let Bad(V , V<k−1) = φ at the beginning of the k-th iteration for some
k. Then Bad(V , V≤k) = φ after the k-th iteration.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 13 / 19

39. 6. Let Bad(V , V<k−1) = φ at the beginning of the k-th iteration for some
k. Then Bad(V , V≤k) = φ after the k-th iteration.
7. Fix k, i and assume that Bad(V , V<k) = φ at the beginning of the i-th
iteration (steps 3 − 13). If there exists a bad path vuv such that v ∈ S
and v ∈ Sc for some iteration jo (of the loop 8 − 12) then vuv is a bad
path in every iteration j < jo of the loop 8 − 12.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 13 / 19

40. 6. Let Bad(V , V<k−1) = φ at the beginning of the k-th iteration for some
k. Then Bad(V , V≤k) = φ after the k-th iteration.
7. Fix k, i and assume that Bad(V , V<k) = φ at the beginning of the i-th
iteration (steps 3 − 13). If there exists a bad path vuv such that v ∈ S
and v ∈ Sc for some iteration jo (of the loop 8 − 12) then vuv is a bad
path in every iteration j < jo of the loop 8 − 12.
8. For every iteration of the loop 8 − 12 either at least one vertex on P
changes its state or state S is on its final distination vs.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 13 / 19

41. 6. Let Bad(V , V<k−1) = φ at the beginning of the k-th iteration for some
k. Then Bad(V , V≤k) = φ after the k-th iteration.
7. Fix k, i and assume that Bad(V , V<k) = φ at the beginning of the i-th
iteration (steps 3 − 13). If there exists a bad path vuv such that v ∈ S
and v ∈ Sc for some iteration jo (of the loop 8 − 12) then vuv is a bad
path in every iteration j < jo of the loop 8 − 12.
8. For every iteration of the loop 8 − 12 either at least one vertex on P
changes its state or state S is on its final distination vs.
9. 0 ≤ q(P) ≤ 2∆2.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 13 / 19

42. Analysis of Algorithm
Theorem
C(k, i) ≤ 2∆2.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 14 / 19

43. Analysis of Algorithm
Theorem
C(k, i) ≤ 2∆2.
Proof.
For a fixed k, i and a vertex v ∈ S in step 6, let P be defined as before.
By Fact 9, q(P ) ≤ 2∆2 and, in view of fact 8, in 2∆2 iterations the state
originated at v will reach its final destination. Since every bad path is
obtained from some v ∈ S, after 2∆2 iterations there will be no bad paths
in Y , that is Y = φ.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 14 / 19

44. Analysis of Algorithm
Theorem
After all iterations of the loop 2 − 14, Bad(V , V ) = φ. In particular, the
semi-matching returned in Step 15 is non-swappable.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 15 / 19

45. Analysis of Algorithm
Theorem
After all iterations of the loop 2 − 14, Bad(V , V ) = φ. In particular, the
semi-matching returned in Step 15 is non-swappable.
Proof.
First note that after the k-th iteration, Bad(V , V≤k) = φ. Indeed, by
induction on k, if k = 0, then Bad(V , V−1) = φ and so, by fact 6,
Bad(V , V≤0) = φ. For the inductive step, assume that
Bad(V , V≤k−1) = φ and thus, by fact 6, Bad(V , V≤k) = φ. Since
∆(V ) ≤ ∆ and there are no bad paths ending in vertices of degree at least
∆ − 1, after all iterations of the algorithm we have
Bad(V , V ) = Bad(V , V≤∆−2) = φ.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 15 / 19

46. Related Works
Authors have developed an algorithm using the distributed algorithms
for computing maximal matching problem, such that the
cost(M) ≤ λ.cost(M∗), where λ = min(3.105, ∆|V |
|U| ) and the time
complexity of the algorithm is O(min(∆2, ∆.log4(|V | + |U|))). (DISC
2011, page 200–201)
Authors have also gave an alternative algorithm GREEDYSM, which
is much faster in the case when ∆ is large, the degrees of vertices of
V do not differ much from each other, and the degrees on U are
bounded from above. (DISC 2012, page 219–221)
Harvey, Lov´asz, Ladner and Tamir have proposed two polynomial time
sequential algorithms based on Hungarian method for computing
maximum bipartite graph and cost reducing paths. (Semi-matchings
for bipartite graphs and load balancing, J. Algorithms)
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 16 / 19

47. Further Improvement
In our algorithm we have only considered bad paths of length 2 i.e. paths
of the form vuw. If we could come up with an efficient swapping operation
for bad paths of length greater than 2, then we might get a better
approximation ratio.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 17 / 19

48. References
A Czygrinow, M Han´ckowiak, E Szyma´nska, W Wawrzyniak (2012)
Distributed 2-Approximation Algorithm for the Semi-Matching Problem
DISC 2012 , 210 – 222.
A Czygrinow, M Han´ckowiak, E Szyma´nska, W Wawrzyniak (2012)
Brief Announcement: Distributed Approximations for the Semi-matching Problem
DISC 2011 , 200 – 201.
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 18 / 19

49. The End
Vishu and Ayan (IIT Guwahati) Semi-Matching Algorithm 19 / 19