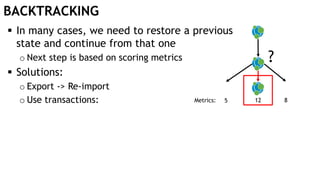
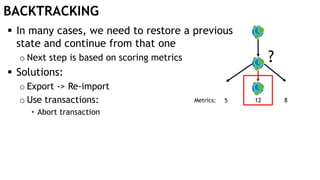
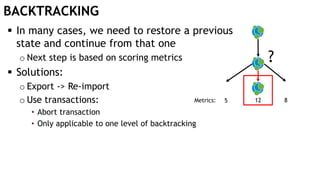
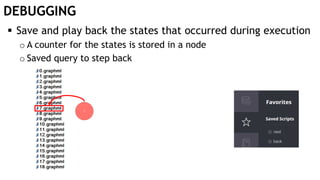
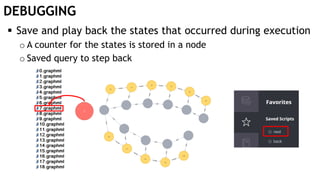
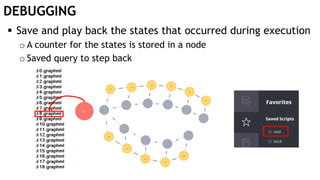
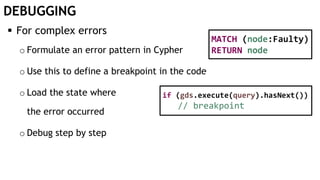
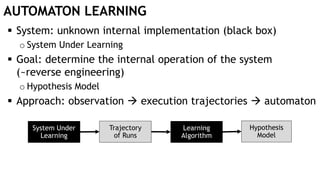
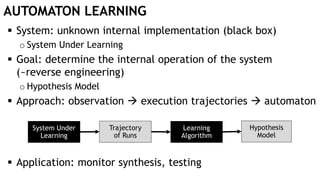
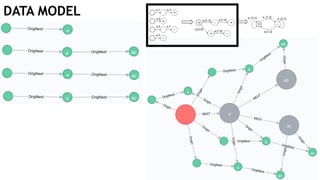
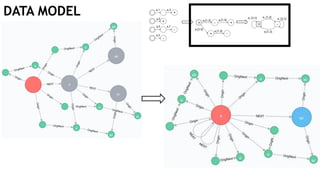
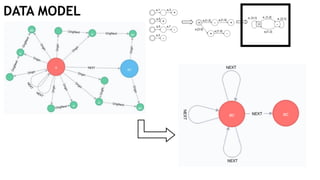
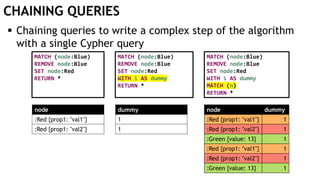
The document discusses learning timed automata using Cypher queries. It provides background on automaton learning, including representing systems as state machines and learning their behavior through observation and experimentation. The goal is to develop a hypothesis model that matches the internal operations of the system under learning. The document outlines the basic automaton learning process and describes an algorithm that repeats splitting inconsistent states, merging similar states, and coloring states to finalize the learned automaton. It also discusses some interesting queries that could be used as part of the learning process in Cypher, such as selecting longest paths and handling inconsistencies that can be transitive when merging states.



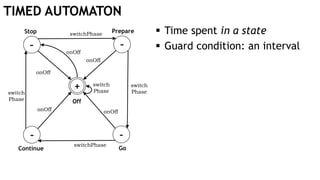
![TIMED AUTOMATON
Time spent in a state
Guard condition: an interval
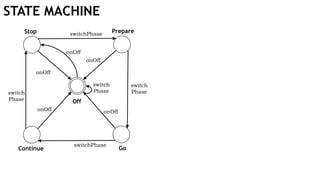
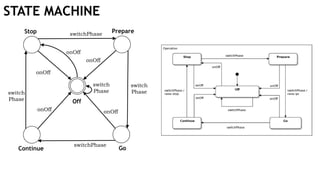
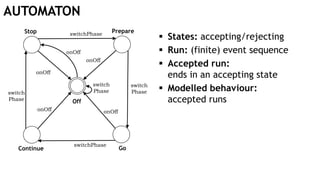
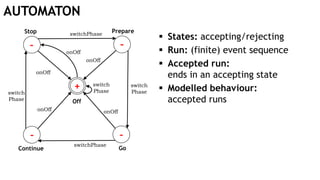
Off
Stop
Continue
Prepare
Go
switchPhase
switchPhase
switch
Phase
onOff
onOff
onOff onOff
onOff
switch
Phase
+
- -
- -
[3,5]
[30,35]
[1,2]
switch
Phase
[30,35]
[0,∞]
[0,∞]
[0,∞]
[0,∞]
[0,∞]
[0,∞]](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-9-320.jpg)




![AUTOMATON LEARNING: THE BASICS
+
-
-
+
a,1
a,5
+
a,3
a,5 a,7
a,2
+ -
a,[1,2]
+
a,[1,5]
+
a,[3,5]
-
a,[1,5]
+ -
a, [1,2]
a,[1,2]
a, [3,5] a, [3,5]](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-16-320.jpg)
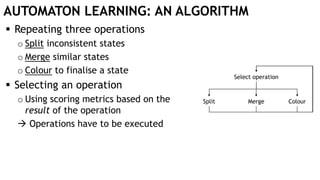
![AUTOMATON LEARNING: AN ALGORITHM
Repeating three operations
o Split inconsistent states
+ -
a,[1,2]
+
a,[1,5]
+
a,[3,5]
-
a,[1,5]
+ +/-
a,[1,5]
+/-
a,[1,5]
+
-
-
+
a,1
a,5
+
a,3
a,5 a,7
a,2](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-17-320.jpg)
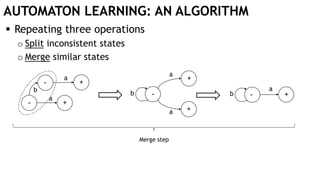







![WHERE NOT «PATTERN»
Finding the beginning of a path
Finding the end of a path
These two can be used to select a complete path
MATCH (u)-[:Next*]->(v) WHERE NOT ()-[:Next]->(u)
MATCH (u)-[:Next*]->(v) WHERE NOT (v)-[:Next]->()
MATCH (u)-[:Next*]->(v)
WHERE NOT ()-[:Next]->(u)
AND NOT (v)-[:Next]->()
u:Next :Next
… …:Next :Next :Next
… …v :Next](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-32-320.jpg)
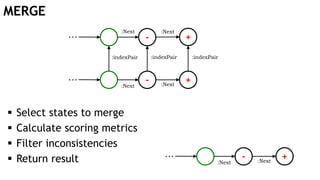
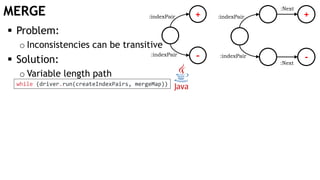
![MERGE +
-
:indexPair
:indexPair
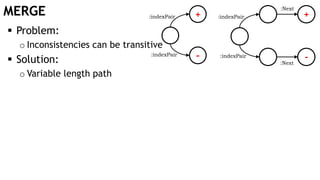
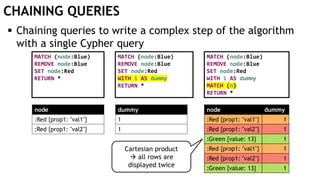
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
:indexPair
:indexPair
+
-:Next
:Next
MATCH (s1:IndexedMerge)-[:IndexPair*..]-(s2:IndexedMerge),
s1p = (s1)-[:Next*0..]->(s12:State), s2p = (s2)-[:Next*0..]->(s22:State)
WHERE id(s1) > id(s2) AND length(s1p) = length(s2p)
AND NOT (s12)-[:IndexPair*0..]-(s22)
WITH s12, s22, s1p, s2p,[s1r IN rels(s1p) | s1r.symbol] AS s1ss, [s2r IN rels(s2p) | s2r.symbol] AS s2ss,
[s1r IN rels(s1p) | s1r.Tmin] AS s1mins, [s2r IN rels(s2p) | s2r.Tmin ] AS s2mins,
[s1r IN rels(s1p) | s1r.Tmax] AS s1maxs, [s2r IN rels(s2p) | s2r.Tmax ] AS s2maxs
WHERE s1ss = s2ss AND s1mins = s2mins AND s1maxs = s2maxs
WITH collect([s12, s22]) as pairs
MATCH ()-[ip:IndexPair]->()
WITH max(ip.index) + 1 as nextIndex, pairs
UNWIND range(0, length(pairs)-1) as idx
WITH pairs[idx][0] as s12, pairs[idx][1] as s22, idx + nextIndex as edgeIndex
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
while (driver.run(createIndexPairs, mergeMap))](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-36-320.jpg)
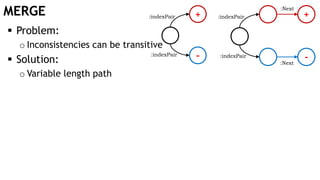
![MERGE
MATCH (s1:IndexedMerge)-[:IndexPair*]-(s2:IndexedMerge),
s1p = (s1)-[:Next*0..]->(s12:State),
s2p = (s2)-[:Next*0..]->(s22:State)
WHERE id(s1) > id(s2) AND length(s1p) = length(s2p)
AND NOT (s12)-[:IndexPair*0..]-(s22)
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Next
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-38-320.jpg)
![MERGE
MATCH (s1:IndexedMerge)-[:IndexPair*]-(s2:IndexedMerge),
s1p = (s1)-[:Next*0..]->(s12:State),
s2p = (s2)-[:Next*0..]->(s22:State)
WHERE id(s1) > id(s2) AND length(s1p) = length(s2p)
AND NOT (s12)-[:IndexPair*0..]-(s22)
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Next
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
Find critical state pairs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-39-320.jpg)
![MERGE
MATCH (s1:IndexedMerge)-[:IndexPair*]-(s2:IndexedMerge),
s1p = (s1)-[:Next*0..]->(s12:State),
s2p = (s2)-[:Next*0..]->(s22:State)
WHERE id(s1) > id(s2) AND length(s1p) = length(s2p)
AND NOT (s12)-[:IndexPair*0..]-(s22)
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Next
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
s1 s1
s2 s2
Find critical state pairs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-40-320.jpg)
![MERGE
MATCH (s1:IndexedMerge)-[:IndexPair*]-(s2:IndexedMerge),
s1p = (s1)-[:Next*0..]->(s12:State),
s2p = (s2)-[:Next*0..]->(s22:State)
WHERE id(s1) > id(s2) AND length(s1p) = length(s2p)
AND NOT (s12)-[:IndexPair*0..]-(s22)
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Next
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
s1 s1
s2 s2
WITH s12, s22, s1p, s2p,
[s1r IN rels(s1p) | s1r.symbol] AS s1ss, [s2r IN rels(s2p) | s2r.symbol] AS s2ss,
[s1r IN rels(s1p) | s1r.Tmin] AS s1mins, [s2r IN rels(s2p) | s2r.Tmin ] AS s2mins,
[s1r IN rels(s1p) | s1r.Tmax] AS s1maxs, [s2r IN rels(s2p) | s2r.Tmax ] AS s2maxs
WHERE s1ss = s2ss AND s1mins = s2mins AND s1maxs = s2maxs
...
Find critical state pairs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-41-320.jpg)
![MERGE
MATCH (s1:IndexedMerge)-[:IndexPair*]-(s2:IndexedMerge),
s1p = (s1)-[:Next*0..]->(s12:State),
s2p = (s2)-[:Next*0..]->(s22:State)
WHERE id(s1) > id(s2) AND length(s1p) = length(s2p)
AND NOT (s12)-[:IndexPair*0..]-(s22)
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Next
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
s1 s1
s2 s2
WITH s12, s22, s1p, s2p,
[s1r IN rels(s1p) | s1r.symbol] AS s1ss, [s2r IN rels(s2p) | s2r.symbol] AS s2ss,
[s1r IN rels(s1p) | s1r.Tmin] AS s1mins, [s2r IN rels(s2p) | s2r.Tmin ] AS s2mins,
[s1r IN rels(s1p) | s1r.Tmax] AS s1maxs, [s2r IN rels(s2p) | s2r.Tmax ] AS s2maxs
WHERE s1ss = s2ss AND s1mins = s2mins AND s1maxs = s2maxs
...
• Paths of same length
• Event sequences of same
lengths, etc.
Find critical state pairs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-42-320.jpg)
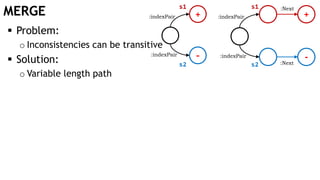
![MERGE
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Nexts1 s1
s2 s2](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-44-320.jpg)
![MERGE
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Nexts1 s1
s2 s2
Mark newly found
index pairs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-45-320.jpg)
![MERGE
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Nexts1 s1
s2 s2
:indexPair :indexPair
Mark newly found
index pairs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-46-320.jpg)
![MERGE
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Nexts1 s1
s2 s2
:indexPair :indexPair
Mark newly found
index pairs
while (driver.run(createIndexPairs, mergeMap))](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-47-320.jpg)
![MERGE
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Nexts1 s1
s2 s2
:indexPair :indexPair
Mark newly found
index pairs
while (driver.run(createIndexPairs, mergeMap))
Repeatedly called from
Java code until fixed-point](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-48-320.jpg)
![MERGE
CREATE (s12)-[:IndexPair {index: edgeIndex}]->(s22)
SET s12:IndexedMerge, s22:IndexedMerge
Problem:
o Inconsistencies can be transitive
Solution:
o Variable length path
+
-
:indexPair
:indexPair
:indexPair
:indexPair
+
-:Next
:Nexts1 s1
s2 s2
:indexPair :indexPair
Mark newly found
index pairs
while (driver.run(createIndexPairs, mergeMap))
Repeatedly called from
Java code until fixed-point](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-49-320.jpg)
![SPLIT
:Origin
:Origin
:Origin
:Origin
[1,6]
1
6
Splits an edge
Based on timestamp: t
o Original transition
The two endpoints…
o Smaller: < t
o Larger: ≥ t
2
:Origin :Origin
+
+
-
+/-](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-50-320.jpg)
![SPLIT
:Origin
:Origin
:Origin
:Origin
[1,6]
1
6
2
:Origin :Origin
Splits an edge
Based on timestamp: 5
o Original transition
The two endpoints…
o Smaller: < t
o Larger: ≥ t
+
+
-
+/-](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-51-320.jpg)
![SPLIT
Splits an edge
Based on timestamp: 5
o Original transition
The two endpoints…
o Smaller: < t
o Larger: ≥ t
Results
[1,4]
[5,6]
+
-](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-52-320.jpg)
![SPLIT
Problem
o Node a is a result of an earlier
merge operation
o The subtree regenerated from
node b should belong to the…
• Larger subtree because of 6
• Smaller subtree because of 1
:Origin
:Origin :Origin
[1,6]
1
6
b
6
:Origin :Origin
…
a](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-53-320.jpg)
![ Solution
o “Shortest” path to node a
o Based on the last number: 6
SPLIT
:Origin
:Origin :Origin
[1,6]
1
6
b
6
:Origin :Origin
…
a](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-54-320.jpg)
![SPLIT
MATCH (r:Red)-[n:Next]->(b:Blue)
WITH r, b, n.Tmax as Tmax, n.Tmin as Tmin, n.symbol as symbol
UNWIND range(Tmin, Tmax-1) AS t
MATCH (b)-[:Next*0..]->(s1:State)-[:Origin]->(so1:OrigState), trace1=(so1)<-[OrigNext*0..]-(redOrigNext:OrigState), (redOrigNext)<-[no1:OrigNext]-(redOrig:OrigState)<-[:Origin]-(r)
WHERE none(x IN nodes(trace1) WHERE (x)<-[:Origin]-(r))
WITH r, b, t, Tmin, Tmax, symbol, s1, no1, so1
MATCH (b)-[:Next*0..]->(s2:State)-[:Origin]->(so2:OrigState), trace2=(so2)<-[OrigNext*0..]-(redOrigNext:OrigState), (redOrigNext)<-[no2:OrigNext]-(redOrig:OrigState)<-[:Origin]-(r)
WHERE none(x IN nodes(trace2) WHERE (x)<-[:Origin]-(r))
WITH t, r, b, s1, s2, toInteger(no1.time)>t as cat1, toInteger(no2.time)>t as cat2, Tmin, Tmax, symbol, so1, so2
WHERE s1 = s2
AND cat1 <> cat2
AND id(so1) < id(so2)
WITH r, b, t, Tmin, Tmax, symbol,
[coalesce(so1.accepting, false), coalesce(so1.rejecting, false)] AS so1ar,
[coalesce(so2.accepting, false), coalesce(so2.rejecting, false)] AS so2ar
WITH
r, b, t, Tmin, Tmax, symbol,
CASE
WHEN so1ar[0] <> so2ar[0] AND so1ar[1] <> so2ar[1] THEN 1
WHEN so1ar = so2ar AND (so1ar = [false, true] OR so1ar = [true, false]) THEN -1 // there is at least one true
ELSE 0
END AS score
WITH r, b, t, sum(score) AS metric, Tmin, Tmax, symbol
ORDER BY metric DESC
LIMIT 1
WITH r, b, t, metric, Tmin, Tmax, symbol
MATCH (b)-[:Next*0..]->(s1:State)-[:Origin]->(so1:OrigState), trace1=(so1)<-[OrigNext*0..]-(redOrigNext:OrigState), (redOrigNext)<-[no1:OrigNext]-(redOrig:OrigState)<-[:Origin]-(r)
WHERE none(x IN nodes(trace1) WHERE (x)<-[:Origin]-(r)) AND toInteger(no1.time)>t
WITH r, b, t, metric, Tmin, Tmax, symbol, collect(so1) as so1s
MATCH (b)-[:Next*0..]->(s2:State)-[:Origin]->(so2:OrigState), trace2=(so2)<-[OrigNext*0..]-(redOrigNext:OrigState), (redOrigNext)<-[no2:OrigNext]-(redOrig:OrigState)<-[:Origin]-(r)
WHERE none(x IN nodes(trace2) WHERE (x)<-[:Origin]-(r)) AND toInteger(no2.time)<=t
RETURN r, b, t, metric, Tmin, Tmax, symbol, so1s, collect(so2) as so2s](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-55-320.jpg)
![SPLIT
:Origin
:Origin :Origin
[1,6]
1
6
6
:Origin :Origin
…
a s2
ao
an
b
Solution
o “Shortest” path to node a
o Based on the last number: 6
MATCH
(a)-[:Next*0..]->(s2:State)-[:Origin]->(b:OrigState),
trace=(b)<-[OrigNext*0..]-(an:OrigState),
(an)<-[no:OrigNext]-(ao:OrigState)<-[:Origin]-(a)
The split candidate in
the original runs](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-56-320.jpg)
![SPLIT
The split candidate in
the original runs
:Origin
:Origin :Origin
[1,6]
1
6
6
:Origin :Origin
…ao
a
an
s2
b
MATCH
(a)-[:Next*0..]->(s2:State)-[:Origin]->(b:OrigState),
trace=(b)<-[OrigNext*0..]-(an:OrigState),
(an)<-[no:OrigNext]-(ao:OrigState)<-[:Origin]-(a)
Solution
o “Shortest” path to node a
o Based on the last number: 6](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-57-320.jpg)
![SPLIT
WHERE none(x IN nodes(trace) WHERE (x)<-[:Origin]-(a))
The shortest possible path, i.e.
a node, from which node a can
only be reached directly.
Solution
o “Shortest” path to node a
o Based on the last number: 6
:Origin
:Origin :Origin
[1,6]
1
6
6
:Origin :Origin
…
a s2
ao
an
b
MATCH
(a)-[:Next*0..]->(s2:State)-[:Origin]->(b:OrigState),
trace=(b)<-[OrigNext*0..]-(an:OrigState),
(an)<-[no:OrigNext]-(ao:OrigState)<-[:Origin]-(a)](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-58-320.jpg)






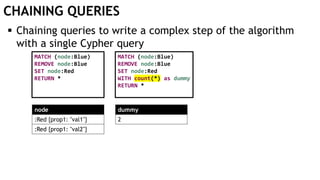
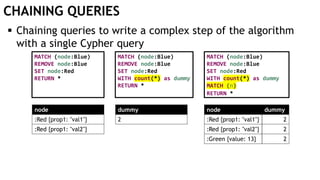
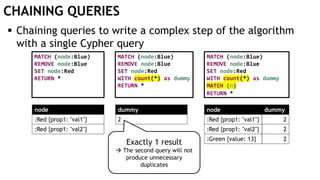
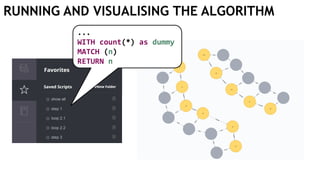
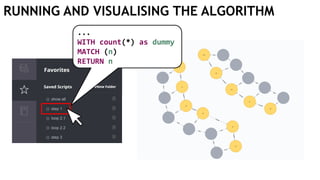
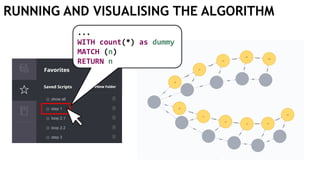
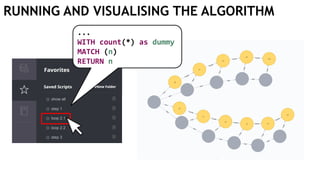
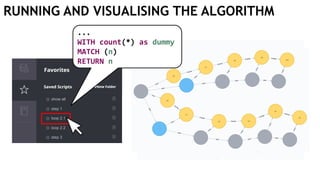
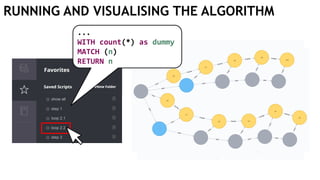
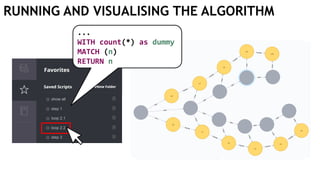
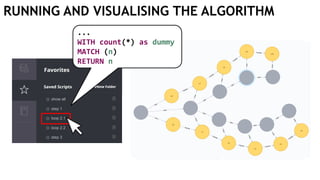
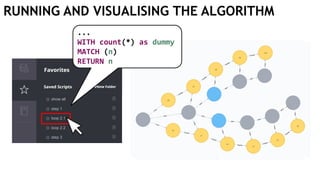
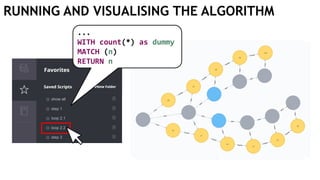
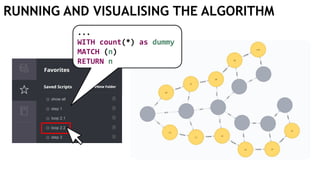
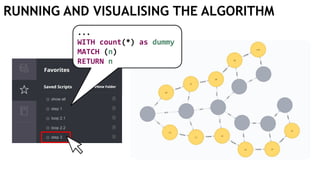
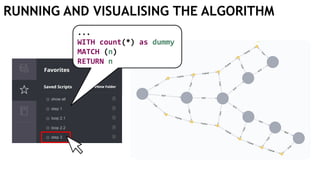

![EXECUTING QUERIES
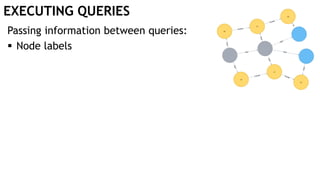
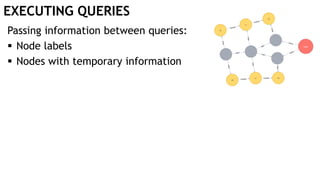
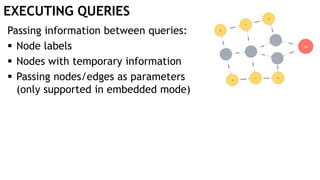
Passing information between queries:
Node labels
Nodes with temporary information
Passing nodes/edges as parameters
(only supported in embedded mode)
redNode num
:Red {prop1: "val1"} 1
WITH $redNode AS redNode
MATCH (g:Green {num: $num})
CREATE (redNode)-[:Edge]->(g)
Exactly
1 result](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-101-320.jpg)
![LOOPS
Many loop-like problems can be solved using lists:
o List comprehensions: [x IN xs WHERE condition | f(x)]
o Reduce: reduce(acc = "", x IN list | acc + x.prop)](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-102-320.jpg)
![LOOPS
Many loop-like problems can be solved using lists:
o List comprehensions: [x IN xs WHERE condition | f(x)]
o Reduce: reduce(acc = "", x IN list | acc + x.prop)
However, loops still might be necessary:
o Run queries from Java code
gds.execute(step1Query);
gds.execute(step2Query);](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-103-320.jpg)
![LOOPS
Many loop-like problems can be solved using lists:
o List comprehensions: [x IN xs WHERE condition | f(x)]
o Reduce: reduce(acc = "", x IN list | acc + x.prop)
However, loops still might be necessary:
o Run queries from Java code
o The loop condition checks the number of rows in the result
while (gds.execute(conditionQuery).hasNext()) {
gds.execute(step1Query);
gds.execute(step2Query);
}](https://image.slidesharecdn.com/ocim4-learning-timed-automata-with-cypher-180531144011/85/Learning-Timed-Automata-with-Cypher-104-320.jpg)