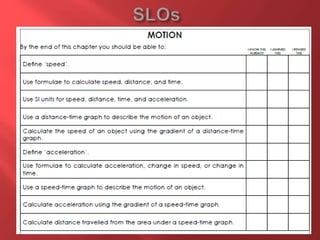
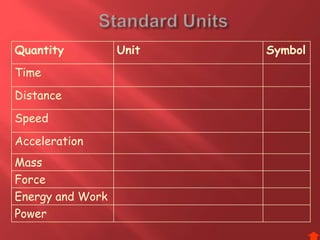
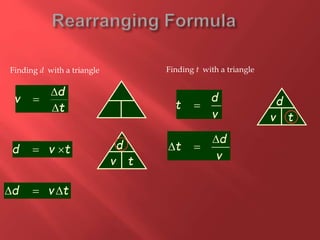
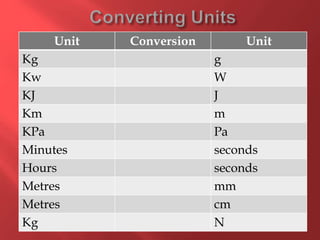
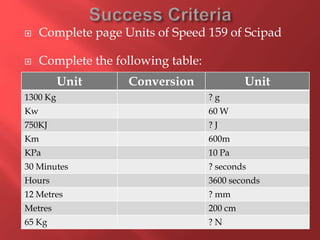
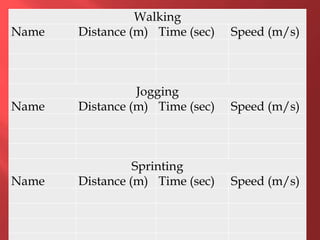
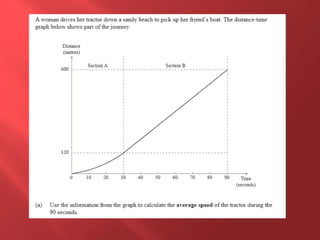
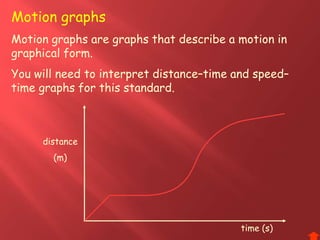
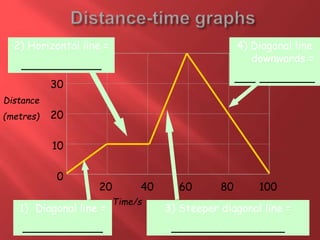
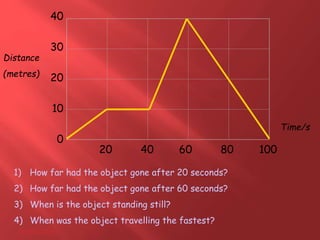
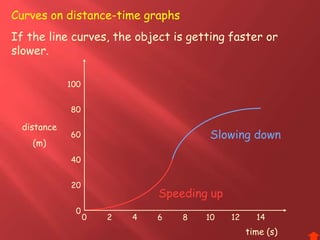
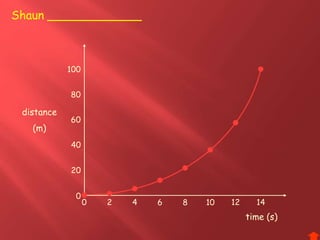
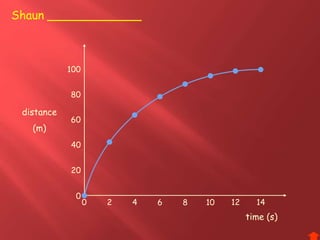
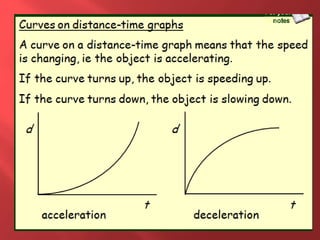
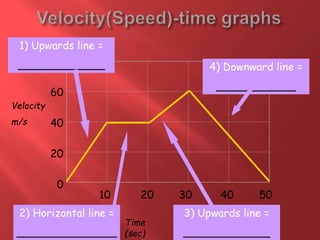
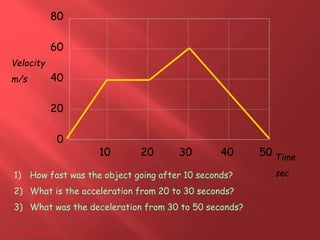
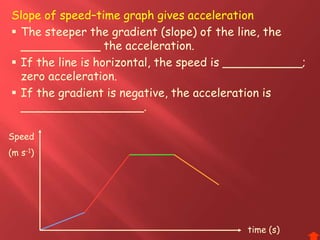
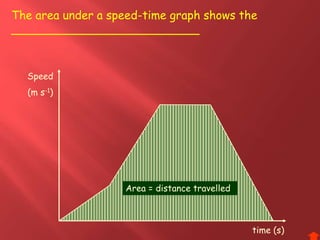
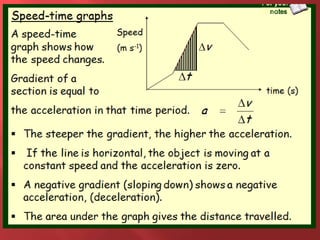
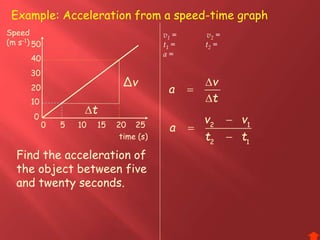
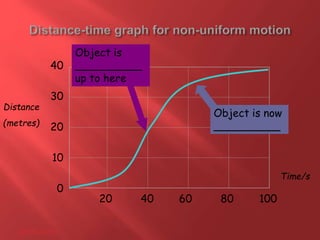
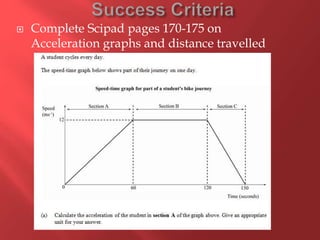
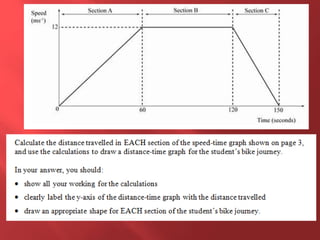
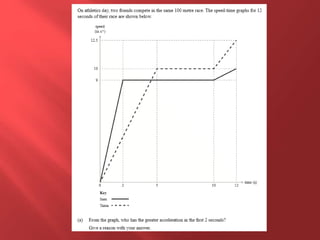
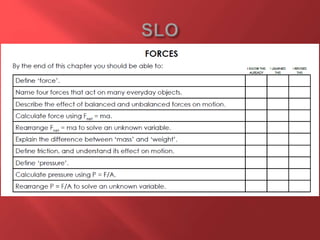
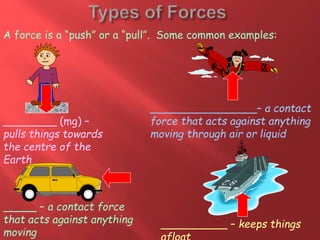
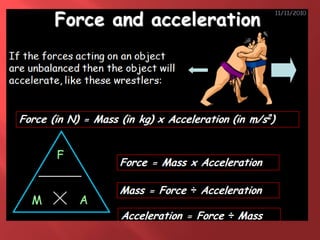
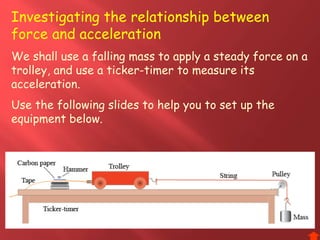
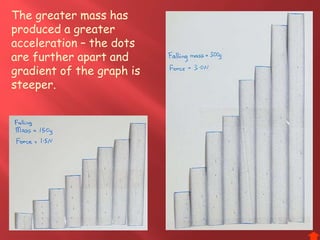
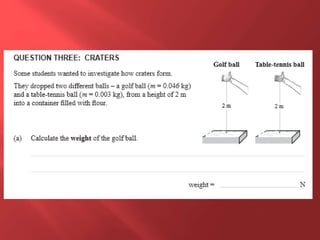
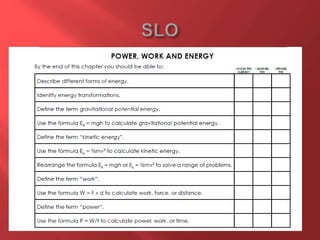
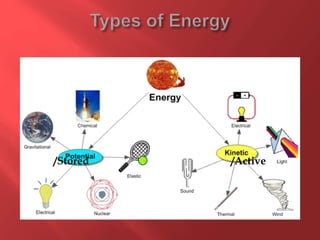
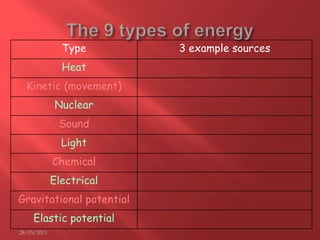
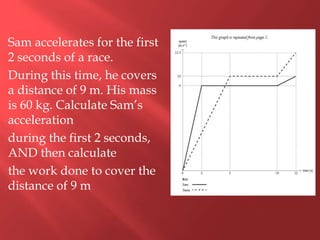
This document provides information about physics concepts related to kinematics including displacement, velocity, acceleration, and their relationships. It defines important terms like speed and acceleration. It presents the key equations for calculating values like speed, acceleration, distance and time. Examples are provided to demonstrate how to set up and solve kinematics problems using the appropriate equations and units. Formulas are given for working with graphs of distance-time and speed-time to determine values and motion. Forces are also introduced along with the key equations for force, mass and acceleration.

1. Year 11
4 External Credits

4. Use SI units for distance, speed, time and
acceleration.

5. Quantity Unit Symbol
Time
Distance
Speed
Acceleration
Mass
Force
Energy and Work
Power

6. t
d
v



d
v
t
d
tv
d v t  d
v t

d v t  
Finding d with a triangle
d
t
v
 d
tv
d
v t

d
t
v

 
Finding t with a triangle

7. Rearranging formulas
Although the formulas are supplied for the exam, they
usually need to be rearranged before being used.
Given: Given:
Given: Given:
d
t
v

  v a t  
F
m
a

work
t
P

d
v
t



v
a
t



F ma
work
P
t

1A 1 Units and formulas
t v
tm

8. If you wanted to know how much you’d grown in the
last year, you’d take your height now and subtract your
height last year:
Change in height = height now – height last year
= 163 cm – 157 cm
= _________
All ‘change in’ calculations in physics are done this way:
change in distance = final distance – initial distance
d = df − di

9. Unit Conversion Unit
Kg g
Kw W
KJ J
Km m
KPa Pa
Minutes seconds
Hours seconds
Metres mm
Metres cm
Kg N

10. _____________________
NOT
 Km/sec or m/hr

11.  Complete page Units of Speed 159 of Scipad
 Complete the following table:
Unit Conversion Unit
1300 Kg ? g
Kw 60 W
750KJ ? J
Km 600m
KPa 10 Pa
30 Minutes ? seconds
Hours 3600 seconds
12 Metres ? mm
Metres 200 cm
65 Kg ? N

12.  Define Speed
http://lgfl.skoool.co.uk/content/keystage3/phys
ics/pc/learnPathLessons/QW5/frameset.htm

13.  An object has speed when it travels a
_____________ in a ___________________.
 ____________ is speed in a given _____________
 Velocity and speed are measured in metres per
second (ms-1) or kilometres per hour (kmh-1)
 Speed and velocity (S or V) = ________________

15. Therefore our formula
Where: v is the symbol for __________
d is the symbol for __________
t is the symbol for __________
t
d
v



is written in an equation as:
timeinchange
distanceinchange
Speed 
The Δ symbol means _____________

16. Speed, distance and time
Distance is how far something moves.
Unit: metre, m
Speed is the rate of change of distance.
Unit: metres per second, m s-1
t
d
v



In equation form this is written as:
Where: v is the symbol for speed, d is the symbol for
distance and t is the symbol for time.
timeinchange
distanceinchange
Speed 
 d = dfinal − dinitial
(Δ means ”change in”.)

17. Scientific calculations
There are a lot of calculations in physics, but once you
master this simple method you will find that they are
all much the same.
1. Sort out the _______ from the question.
2. ____________the relevant formula, rearranging if
necessary (eg to find current instead of voltage).
3. Put the data from the ________ in the formula.
4. __________the answer and write it down with the
correct _________
You will not get ________ marks in an exam unless
you show working (at least steps 2–4).

18. Example: calculating speed
t
d
v



How fast is John moving if he covers in ?
d = ,
s12
m60
v
1-
sm5v
t = , v =s12 s12 see answer
s12 s12
m60 m60
How fast
?
m60
v
m60
1. Sort out the ________.
2. Write the _________.
3. Plug in the ________.
4. Write the answer with
its _________.

19. Example: Calculating speed
t
d
v



How fast is John moving if he covers in ?
d = ,
s12
m60
v
1-
sm5v
t = , v = ?s12 s12
s12
m60 m60
m60
Sort out the data from the question.
Write the relevant formula.
Put the data into the formula.
Calculate the answer and write the correct unit.

20. Example: Calculating distance
d =v =
1-
sm6 t =
How far does Samantha travel if she runs at
for ?
?
How far
1-
sm6
minutes10 minutes10
t
d
v


 Rearranging
d
tvv t
tvd 
d
d 
1-
sm6
Minutes is not an SI unit:
convert it into seconds.

21. Aim:
To find out the walking, jogging and sprinting
speeds in m/s for yourself and members of your
group.
Method:
1. Mark out 20m
2. Have a starter with stop watch
3. Have a person at finish line to raise hand when
person crosses it.
4. Record time in seconds to the nearest whole
second

22. Walking
Name Distance (m) Time (sec) Speed (m/s)
Jogging
Name Distance (m) Time (sec) Speed (m/s)
Sprinting
Name Distance (m) Time (sec) Speed (m/s)

23. 1. The parachutist falls through a distance of 400 m
during the first 60 seconds. Calculate the average
speed of the parachutist during this time.
(remember to show ALL working)
2. Complete scipad pages 160-162 Calculating Speed,
Using Triangles and More Speed Calculations

26.  Use distance time graph to describe the motion
of an object
 Calculate the speed of an object using the
gradient of a distance-time graph.

27. Motion graphs are graphs that describe a motion in
graphical form.
You will need to interpret distance–time and speed–
time graphs for this standard.
distance
(m)
time (s)
Motion graphs

28. 28/05/2015
40
30
20
10
0
20 40 60 80 100
4) Diagonal line
downwards =
____________
3) Steeper diagonal line =
_________________
1) Diagonal line =
____________
2) Horizontal line =
____________
Distance
(metres)
Time/s

29. 28/05/2015
40
30
20
10
0
20 40 60 80 100
1) How far had the object gone after 20 seconds?
2) How far had the object gone after 60 seconds?
3) When is the object standing still?
4) When was the object travelling the fastest?
Distance
(metres)
Time/s

31. If the line curves, the object is getting faster or
slower.
Speeding up
Slowing down
0 2 4 6 8 10 12 14
20
40
60
80
100
distance
(m)
time (s)
0
Curves on distance-time graphs

32. Shaun _____________
0 2 4 6 8 10 12 14
20
40
60
80
100
distance
(m)
time (s)
0

33. Shaun _____________
0 2 4 6 8 10 12 14
20
40
60
80
100
distance
(m)
time (s)
0

35.  Complete Scipad pages Distance – Time graphs
pages 163-167.

36.  Define acceleration
 Use formulae to calculate acceleration, change
in speed or change in time

37. Acceleration is the rate of change of speed:
Acceleration
_____________is when an object either speeds up or
slows down.
timeinchange
speedinchange
onaccelerati 
Acceleration is measured in metres per second
squared, _______________
 Acceleration is ________ when speeding up.
 Acceleration is ___________ when slowing
down.
 Slowing down is also called ___________.

38. In an equation this is written as:
Where: a is the symbol for ___________.
v is the symbol for ___________.
t is the symbol for ____________.
Remember Δ means ”change in”.
t
v
a




39. Example: Calculating acceleration
How quickly is Brian accelerating if he increases his
speed from to in ?
1-
sm10
1-
sm20 s5
1-
sm10
1-
sm20 s5
i) Change in speed
if ddd 
d 
ii) Calculate acceleration
t
d
a



a
v
v

40. Example: Calculating speed from acceleration
t = ,a = ,
t
v
a



If Sam accelerates from rest at for ,
what is his final speed?
tav 
v
v =
Rearranging
v
ta
v
a t

?

2-
sm2.5 s5
final speed
2-
sm2.5 s5
‘From rest’ means his speed started out at zero.

41.  Complete page 168-169 Scipad, Acceleration

42.  Use speed-time graphs to describe the motion
of an object
 Calculate acceleration using the gradient of a
speed-time graph
 Calculate the distance travelled from the area
under a speed-time graph

45. Each strip shows the distance travelled by the trolley
over the 0.1 s interval.
We have made a speed-time graph of the trolley’s
journey as it slowed down.
1B 4 Testing ticker-timers 1B 5 Going dotty

46. 28/05/2015
80
60
40
20
0
10 20 30 40 50
Velocity
m/s
Time
(sec)
1) Upwards line =
_____________
2) Horizontal line =
_______________
3) Upwards line =
_____________
4) Downward line =
____________

47. 28/05/2015
80
60
40
20
0
1) How fast was the object going after 10 seconds?
2) What is the acceleration from 20 to 30 seconds?
3) What was the deceleration from 30 to 50 seconds?
10 20 30 40 50
Velocity
m/s
Time
sec

48. Slope of speed–time graph gives acceleration
 The steeper the gradient (slope) of the line, the
___________ the acceleration.
 If the line is horizontal, the speed is ___________;
zero acceleration.
 If the gradient is negative, the acceleration is
_________________.
Speed
(m s-1)
time (s)

49. Speed
(m s-1)
time (s)
The area under a speed-time graph shows the
__________________________
Area = distance travelled

51. Find the acceleration of
the object between five
and twenty seconds.
v
a
t



v1 = v2 =
t1 = t2 =
a =
2 1
2 1
v v
a
t t



Speed
(m s-1)
time (s)
0
0 5 10 15
20
40
20
10
30
50
25
Δv
t
Example: Acceleration from a speed-time graph

52. 28/05/2015
40
30
20
10
0
20 40 60 80 100
Distance
(metres)
Time/s
Object is
__________
up to here
Object is now
__________

53.  Complete Scipad pages 170-175 on
Acceleration graphs and distance travelled

56.  Complete Scipad pages 176-181, 158
 Complete worksheets
 Complete purple book pages

58.  Define Force
 Name the four forces that act on many
everyday objects

59.  Force (F) has both ___________ and _________
 Force is measured in __________
 Forces are drawn as _________, the arrow head
shows the _________ and the __________ shows
the __________of the force.
28/05/2015

60.  http://lgfl.skoool.co.uk/content/keystage3/Physics/pc/learning
steps/FCDLC/launch.html
28/05/2015

61. 28/05/2015
A force is a “push” or a “pull”. Some common examples:
________ (mg) –
pulls things towards
the centre of the
Earth
________________– a contact
force that acts against anything
moving through air or liquid
__________ – keeps things
_____ – a contact force
that acts against anything
moving

62.  Complete Scipad page 183-
 Section B is a student cycling at a constant
speed:

63.  Describe the effect of balanced and unbalanced
forces on motion

64. The movement or lack of it, of an object depends on
the forces acting on it.
 Balanced forces = ________________________
 Unbalanced forces = ______________________
Whatever direction the force is greatest in will be the
direction, in which the object moves.
28/05/2015

66. Calculate for using F=ma

69. Investigating the relationship between
force and acceleration
We shall use a falling mass to apply a steady force on a
trolley, and use a ticker-timer to measure its
acceleration.
Use the following slides to help you to set up the
equipment below.

70. The dots on the tape get further apart, indicating that
the trolley was accelerating.
Results

71. Mark off every 5th
dot...
... cut up the tape...
... and join the strips
together to make a
speed-time graph.

72. Label your finished graph with the mass used.

73. Repeat the
experiment using a
mass of 300 g.
5 x 50 g weights
plus
1 x 50 g carrier

74. The greater mass has
produced a greater
acceleration – the dots
are further apart and
gradient of the graph is
steeper.

75. The gradient of the
second graph is exactly
double that of the first.
When the force pulling
the trolley doubles, its
acceleration doubles.

76. Force, acceleration and mass
An unbalanced force acting on an object will cause it to
_______________.
We know now that the acceleration produced is
proportional to the force.
We could carry on making ticker-tape graphs to show
the relationship between acceleration and mass for a
constant force.
Another way to think of the relationship between
force, mass and acceleration is to imagine pushing
cars.

77. The greater the force on the car, the f_________ it
will accelerate.
Pushing cars

78. If the forces are equal but the mass is doubled, then
the acceleration __________.

79. Two people pushing two cars has the _______
acceleration as two separate people each pushing one

80. We have seen that acceleration goes up as force goes
up, and acceleration goes up as mass goes down.
Thus:
or
force
acceleration =
mass
WhereF, force is measured in newtons (N)
m, mass, is measured in kilograms (kg)
And a, acceleration, is measured in metres per second
squared (m s–2)

82.  http://multimedia.mcb.harvard.edu/anim_rhi
no.html
 Complete Scipad pages 186-187

83. Explain the Difference between mass and weight

84.  Mass is the bulk of an object, the amount of
__________ there is
 remains ___________ (is unaffected by gravity)
 measured in ___________________
 _______________are used to compare the mass
of two objects

85.  Gravity is a force which
______________(matter) together
 The bigger the masses the greater the
__________
 The acceleration due to earth’s gravitational
pull is _______________

86.  Weight is the force of __________ on a mass
 also known as __________ force
 measured in ________________
 varies depending on the _________acting on a
mass (greater the gravitational force, greater the
weight), which changes on different planets
 Measured with a ___________ in _________

87. WEIGHT = MASS X GRAVITATIONAL FORCE
Weight = mg g = 10 ms-2 on Earth mass = Kg
. . . so when we say my weight is 65Kg we actually
mean . . .
If my mass is 65 Kg and
I weigh (65 Kg X 10 ms-2) 650 Newton’s

88. An astronaut has a mass of 80 kg.
On Earth her weight is given by:
gm Weight
On the Moon g = 1.7 N kg–1 and her
weight is 136 N.
Her mass on the Moon is the same
as it is on Earth: ________.
gm Weight

89.  Complete scipad page 188-189
A car now hangs motionless on the end of a crane’s
cable. The force applied by the crane is 13 000 N.
Use the value of the crane’s force to determine the
mass of the car. Give an appropriate unit for you
answer.
In your answer, you should include an explanation of
the difference between mass and weight.
HINT: Gravity on earth is 10 ms-2 )

91. Define Friction and understand its
effect on motion

92. On Earth, _____________acts as a
__________opposing the motion (it pushes in the
opposite direction to your movement).
Air resistance or friction only happens when an object
is moving.
Friction
forceGoing up
Stopped at the top

93. As the speed of a falling object increases, its air
resistance ________________.
Eventually the friction force (air resistance) is equal
to the __________________.
When the forces are balanced, the object stops
accelerating. Physicists say that the object has
reached ___________.
A parachute has a large surface
area, giving it a high
______________. With the
parachute open, the sky-diver
slows down until the forces again
balance at a much slower
______________

95. Gravity is the force that makes objects _______.
Gravity is __________pulling objects down, whether
they are moving downwards, stationary, or going up.
All falling objects in the same gravitational field will
accelerate at the same rate (_________________).
Gravity and falling
Here an astronaut on the Moon
dropped a hammer and a feather.
Without air resistance, the
hammer and the feather fall with
the same acceleration and land
____________________.
See the drop online.
feather

96.  Complete Scipad page 190-191

97. Calculate pressure using P=F/A
Rearrange P=F/A to solve an unknown variable

98. Where Pressure,
Force,
Area,
Do you weigh less when you stand on
one leg? Of course not. Since your
weight is now spread over a smaller
area, the pressure on the ground under
your foot is greater.

force
pressure
area
Why are wooden
floors often
damaged when
people wear
stiletto heels?
PressureD

99. If you walk through snow in ordinary
shoes, you’ll _________and your
shoes will get wet.
Snow shoes have a
______________that distributes
the weight of the wearer over a
larger area, reducing the
__________ on each patch of snow.
The caterpillar tracks on
military tanks also reduce
the _______ on the ground
by __________ the surface
area of contact.

101.  Complete scipad pages 192-199, 182

104. The image shows an example of a crater produced
by the golf ball. The students found that the golf
ball always produced a deeper crater than the
table-tennis ball.
Explain why the golf ball produces a deeper
crater than the table-tennis ball, even though the
balls are the same size and shape, and dropped
from the same height

106. Describe different forms of energy
Identify energy Transformations

107.  Energy is the ability to __________
 Energy is measured in ____________

108. /Stored /Active

109. 28/05/2015
Type 3 example sources
Heat
Kinetic (movement)
Nuclear
Sound
Light
Chemical
Electrical
Gravitational potential
Elastic potential
Type 3 example sources

110.  Complete Scipad page 201

111. Energy can neither be _________
nor it is _________, however
energy can be ____________-from
one form of energy to any other
form of energy

112. To describe an energy change for a light bulb we need
to do 3 steps:
Electricity Light + heat
1) Write down the starting
energy:
3) Write down what energy
types are given out:
2) Draw an arrow
What are the energy changes for the following…?
1) An electric fire
2) A rock being dropped from a cliff
3) An arrow being fired

113. What are the energy changes for the
following…?
1) An electric fire
1) A rock dropping from cliff
1) An arrow being fired?

114.  Complete Scipad pages 202

115. Define the term gravitational potential
energy
Use the formula Ep=mgh to calculate
gravitational potential energy

116.  Gravitational potential energy is the energy due to
an object’s ______________ above ground.
 To get an object off the ground, _________ must
have been done to move it
 Gravitational Potential Energy Ep
Fw = m x g (mass x gravity (10))
h = height (metres)

117. What factors determine the climber’s
gravitational potential energy (Ep) in
joules?
His __________in metres – the higher
he climbs, the ________ energy he
had to put in, and the greater his Ep.
His ____________in kilograms – the
heavier he is, the _________ energy
is needed to overcome gravity for the
climb.
The _________ due to gravity (g) in
m s–2 – it’d be much _________ to do
this climb on the Moon.
Thus:
ΔEp = m g Δh

118. E.g. 1
Calculate the gravitational potential energy of a
400Kg pile driver if it can fall 3 metres. G =
10NKg-1
Ep = m x g x h
=

119. A weightlifter lifts a 120 Kg barbell 2.4 metres above the
ground.
What is the weight of the barbell (g = 10NKg-1)
Weight Fgravity = mg
=
How much work is done lifting the barbell?
Work = Fd
=
What is the gravitational potential energy of the barbell at the
top of the lift?
Ep = m x g x h
=

120.  Complete Scipad page 203

121. Define the term kinetic energy
Use the formula Ek= 1/2mv2 to
calculate kinetic energy

122. Kinetic energy (Ek) is the energy of ________objects.
The greater an object’s __________, the greater its
kinetic energy.
If two objects are travelling at the same speed, the
one with the greater ___________ has more kinetic
energy.
Where Ek is the kinetic energy in __, m is mass in kg,
v is __________in m s-1.
Notice that when mass is ________, Ek doubles, but
when ________ is doubled, Ek goes up by a factor of
__________ (22). (faster you go the bigger the mess)
Kinetic energy

123.  The energy possessed by a moving object is called
____________
 Kinetic Energy Ek Kinetic Energy = ½ mv2
 M = mass Kg, v = velocity or speed in m/s
 No movement = ________________
 Kinetic energy depends on the ___________of the
velocity, so if velocity is double, kinetic energy
increases four times
 So a car going twice as fast has ______________the
amount of kinetic energy to lose before it will stop
(four times the breaking distance)

124. E.g.
Calculate the kinetic energy of a 5 Kg cat running
at 2m/s
Kinetic Energy = ½ mv2
=
Task:
Complete questions 1-3 purple book page 144

125.  Complete scipad page 204-206
Rosemary skis down a slope in a straight line, as
shown in the diagram below. At the bottom of the
slope, her speed is 8 ms-1. The combined mass of
Rosemary and her skis is 80 kg.
Calculate the kinetic energy of Rosemary and her skis
as she reaches the bottom of the slope when she is
moving at 8 ms-1. Give an appropriate unit for your
answer.

126. The kinetic energy gained by Rosemary when she reached
the bottom of the slope does not equal the energy she had
when she was stationary at the top of the slope.
Explain using the principles of physics why her energy at
the top of the slope and her energy at the bottom of the
slope are not equal.
In your answer, you should:
 name the type of energy Rosemary has at the top of the
slope
 calculate the difference between her kinetic energy at
the bottom of the slope and her energy at the top of the
slope
 justify the difference between her kinetic energy at the
bottom of the slope and her
energy at the top of the slope.

127. Define the term work
Use the formula W=Fxd to calculate
work, force or distance

128.  Work is done when a _______________an object over a
distance
 If work is done to an object, then ___________is
transferred
 The gain in energy is _____________ to the work done
 Work is in joules (J), Energy is in joules (J)
 Work done = _______________
 Work done =

No movement = no work!

129. E.g.
Calculate the work done when a 12 N force moves an
object through 0.2 m
W = Fd
 Complete questions 1-4 on page 135 purple book

130.  Complete scipad page 207-208
A crane lifting a car from the bottom of a cliff.
The cable of the crane pulls the car with a force of
14 000 N for 25 seconds but is not able
to move it
Explain why no work has been done on the car
even though the cable pulls with a force of
14 000 N for 25 s.

131. Sam accelerates for the first
2 seconds of a race.
During this time, he covers
a distance of 9 m. His mass
is 60 kg. Calculate Sam’s
acceleration
during the first 2 seconds,
AND then calculate
the work done to cover the
distance of 9 m

133. Define the term power
Use the formula P= W/t to calculate
power, work or time

134.  Power is a measure of ________________at which
work is done or energy is supplied or used.
 Power P watts
E.g.
A weight lifter lifts a weight in 3.5 seconds. The work
done is 2880J (this can be calculated from Wk = Fd).
Calculate the power that his muscles generated.
P = W/t
=
 Complete questions -4 on page 150 purple book

135.  Complete Scipad pages 209-215
A force of 16 000 N is used to pull a car upwards
using a crane. The car is lifted 24 m over a period
of 80 s.
Calculate the power output of the crane to pull
the car up 24 m. Give an appropriate unit for your
answer. (HINT: you need to calculate work done
first)