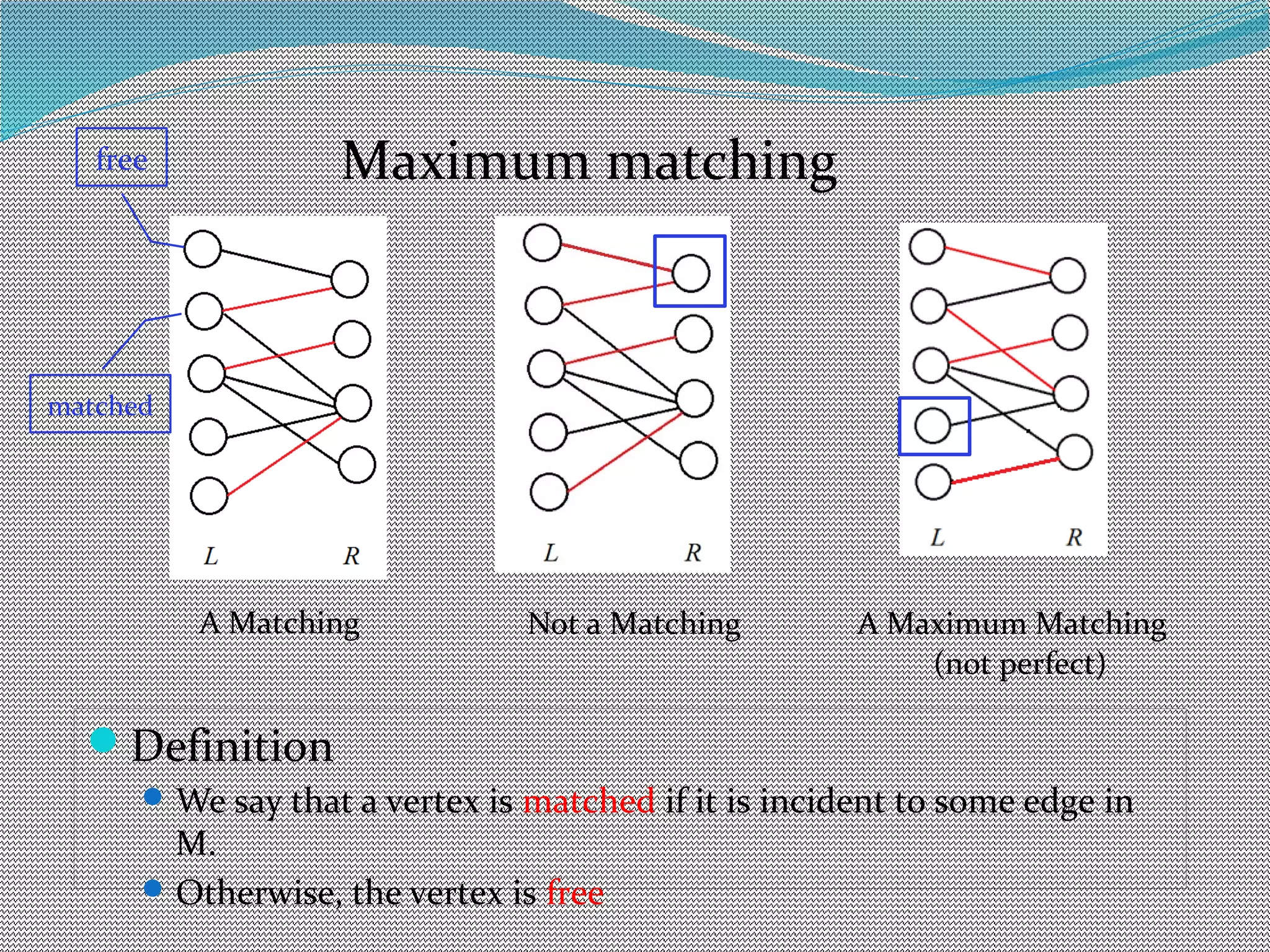
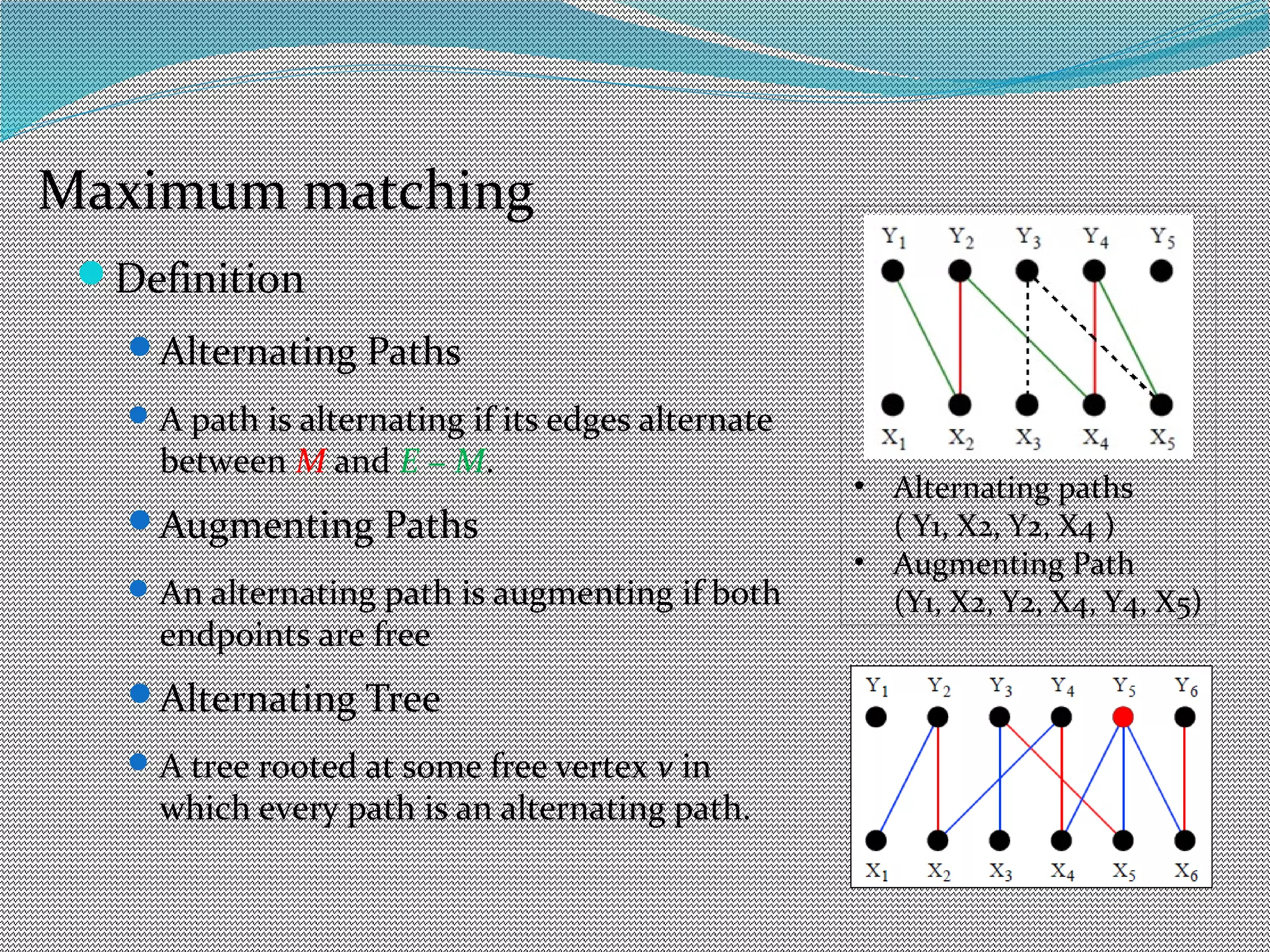
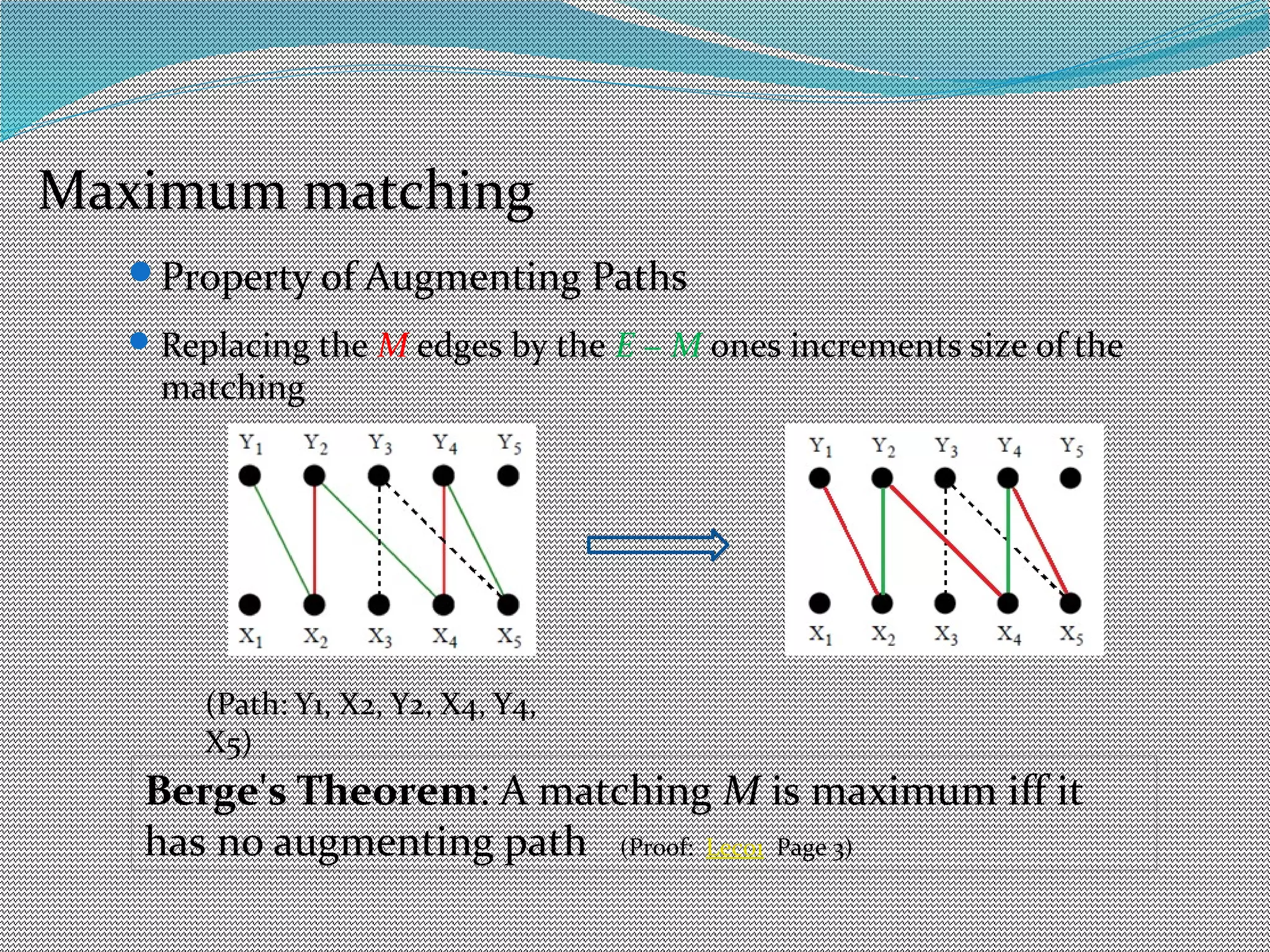
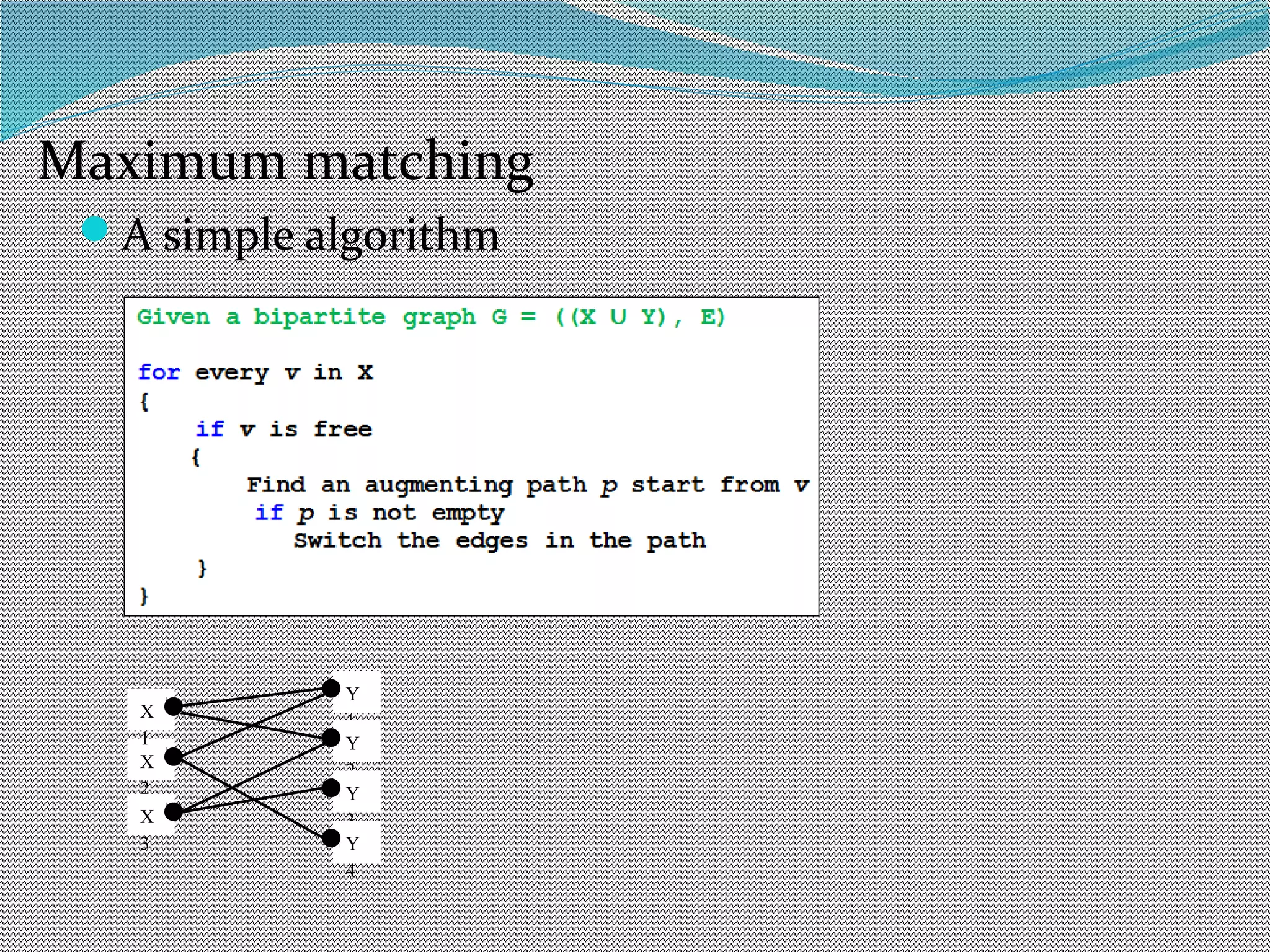
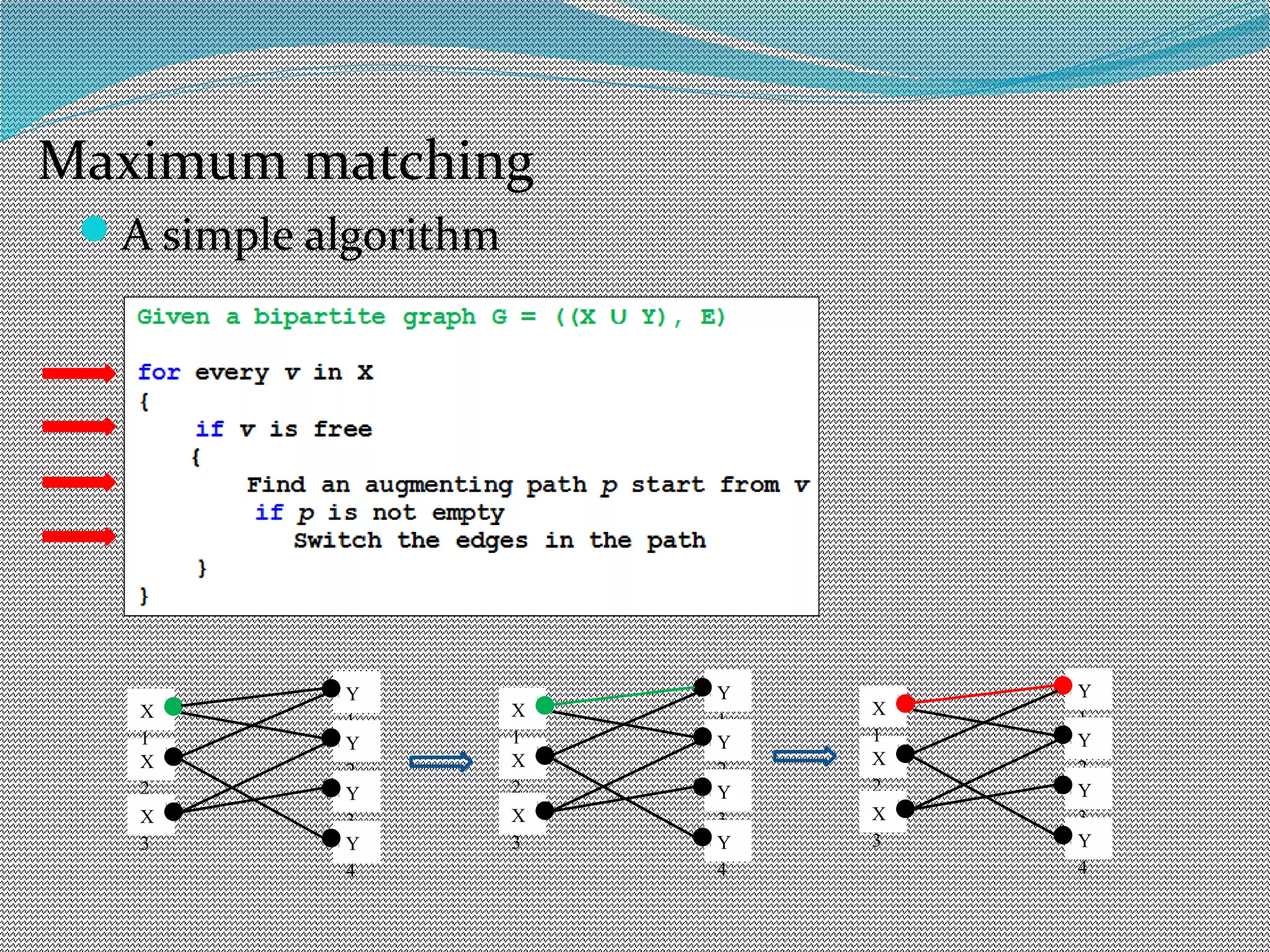
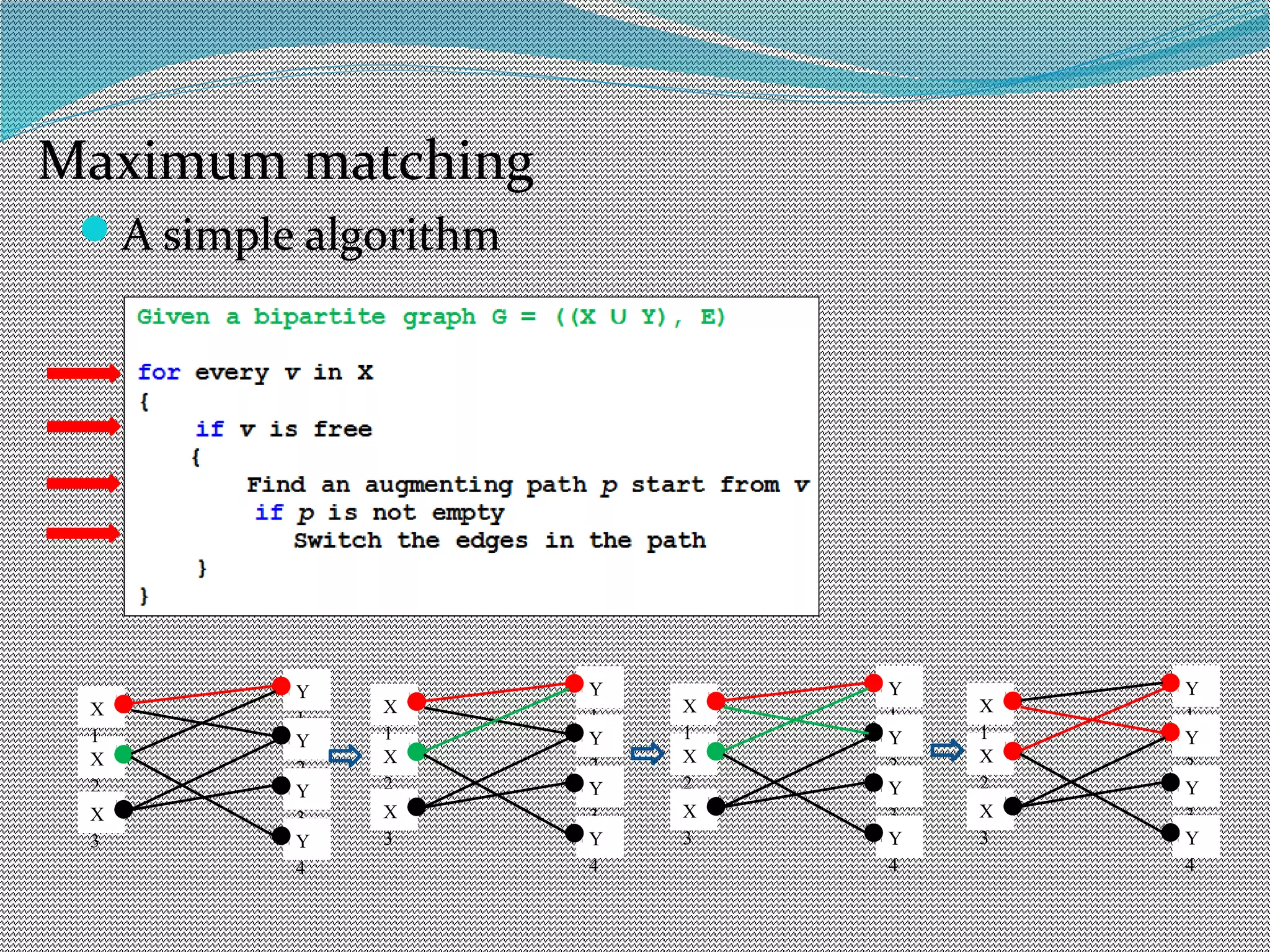
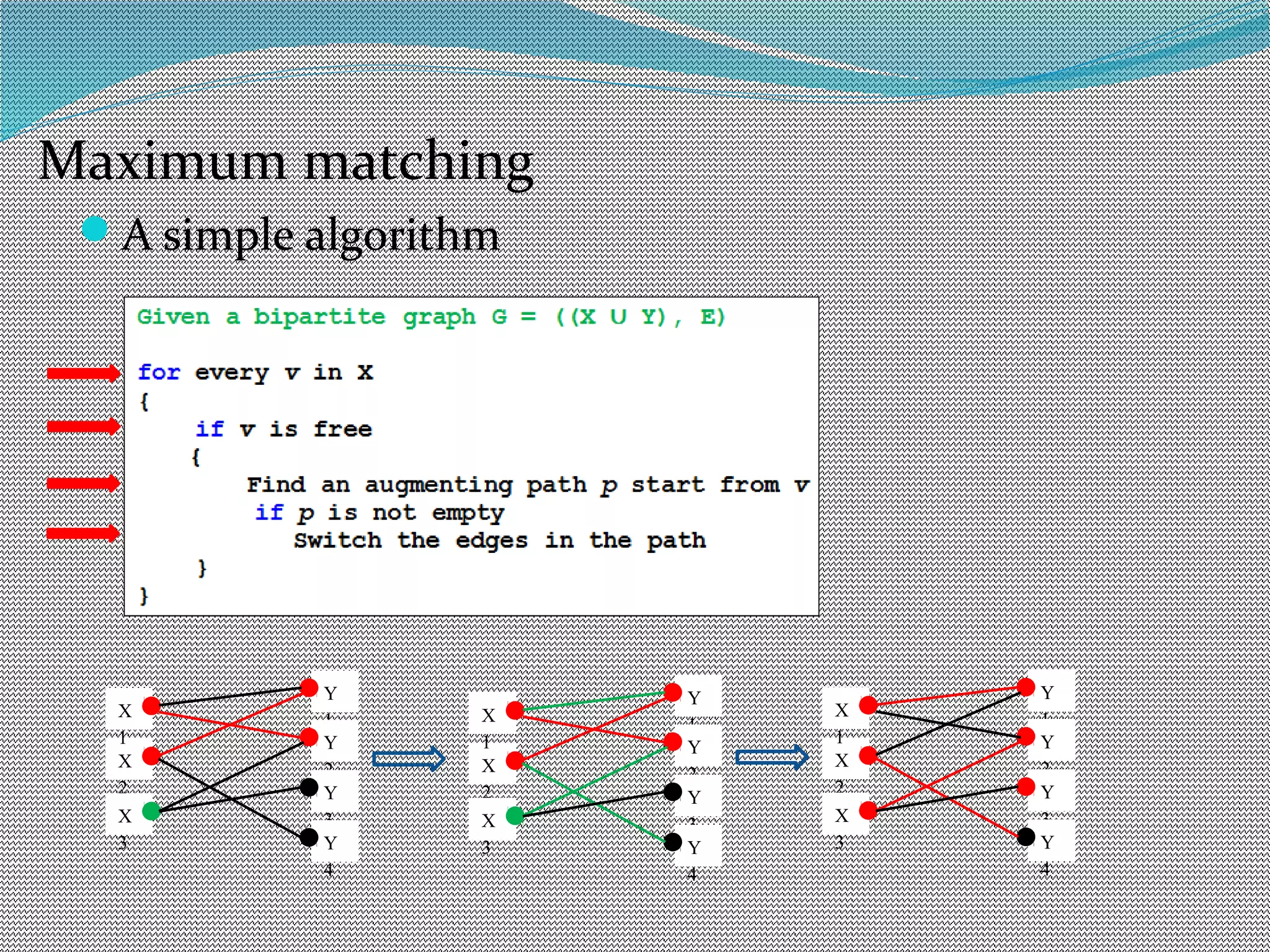
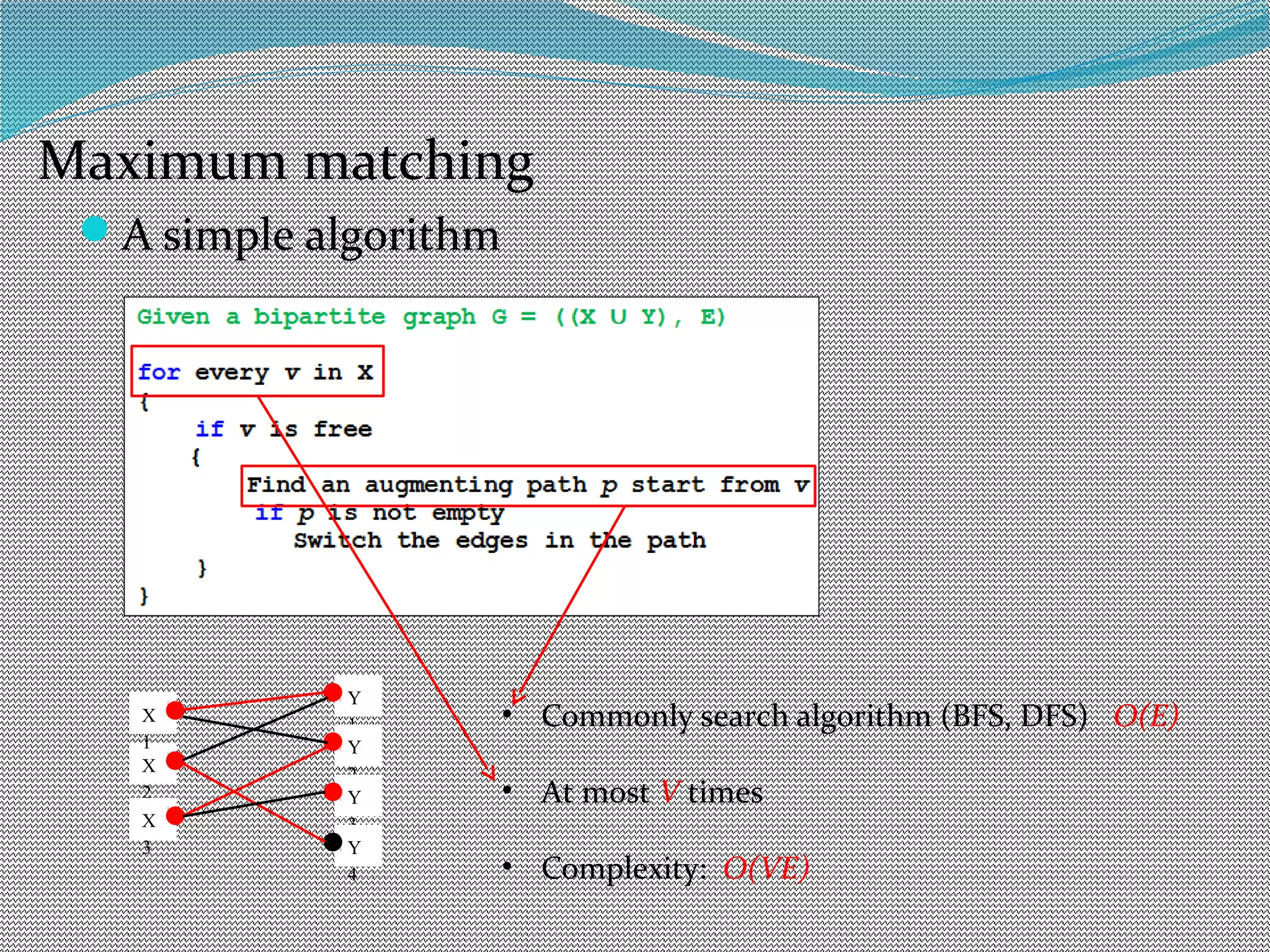
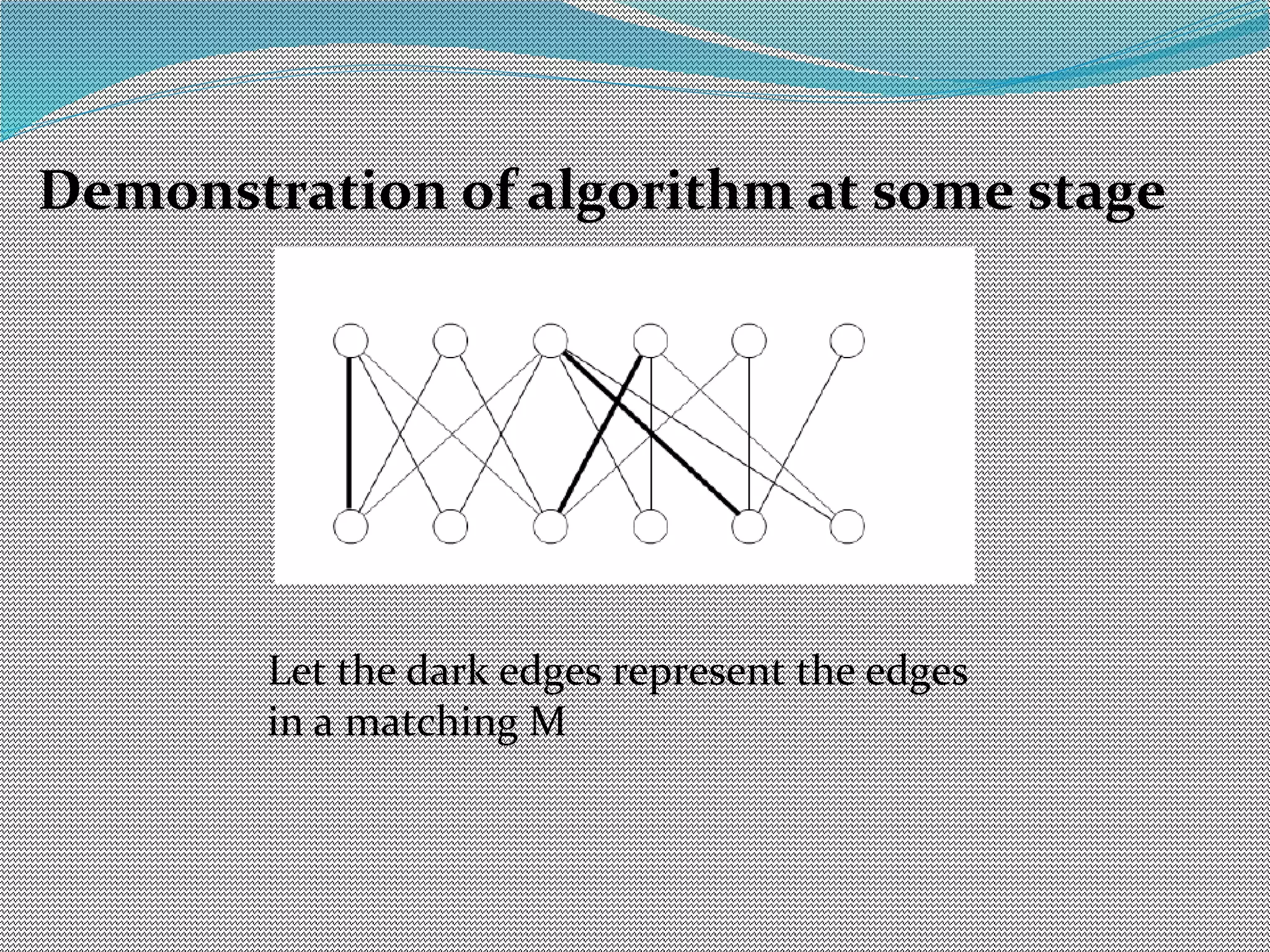
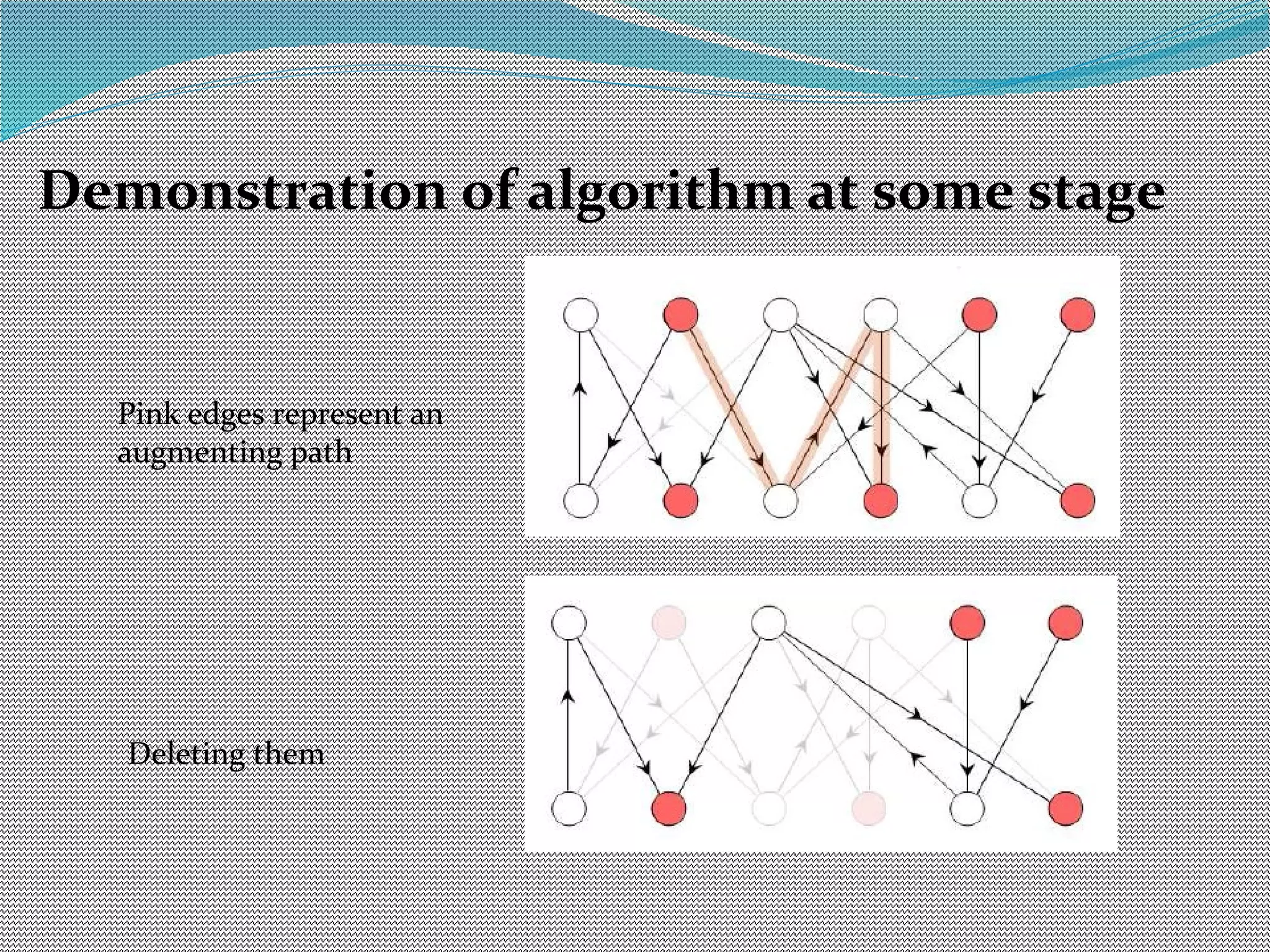
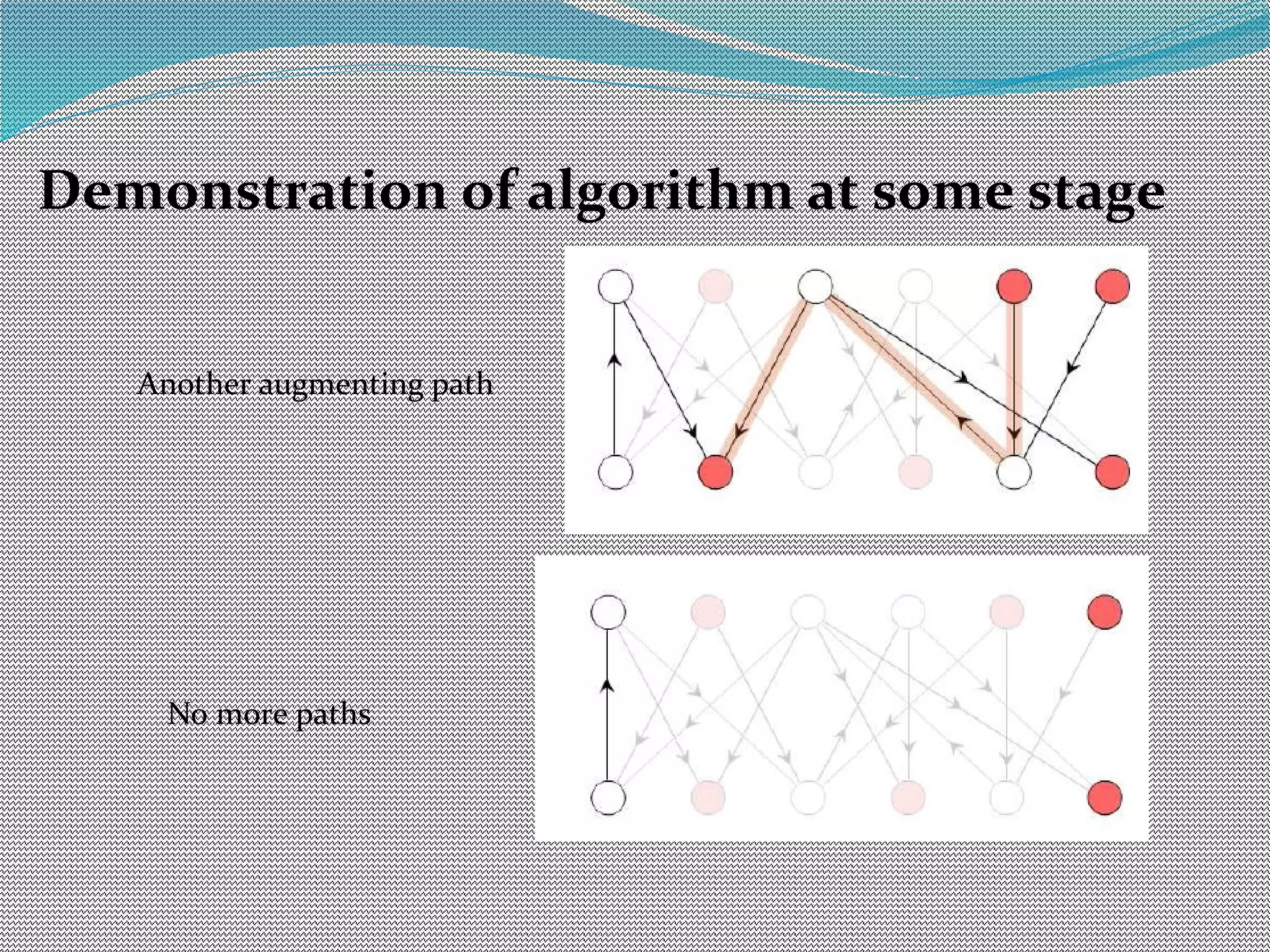
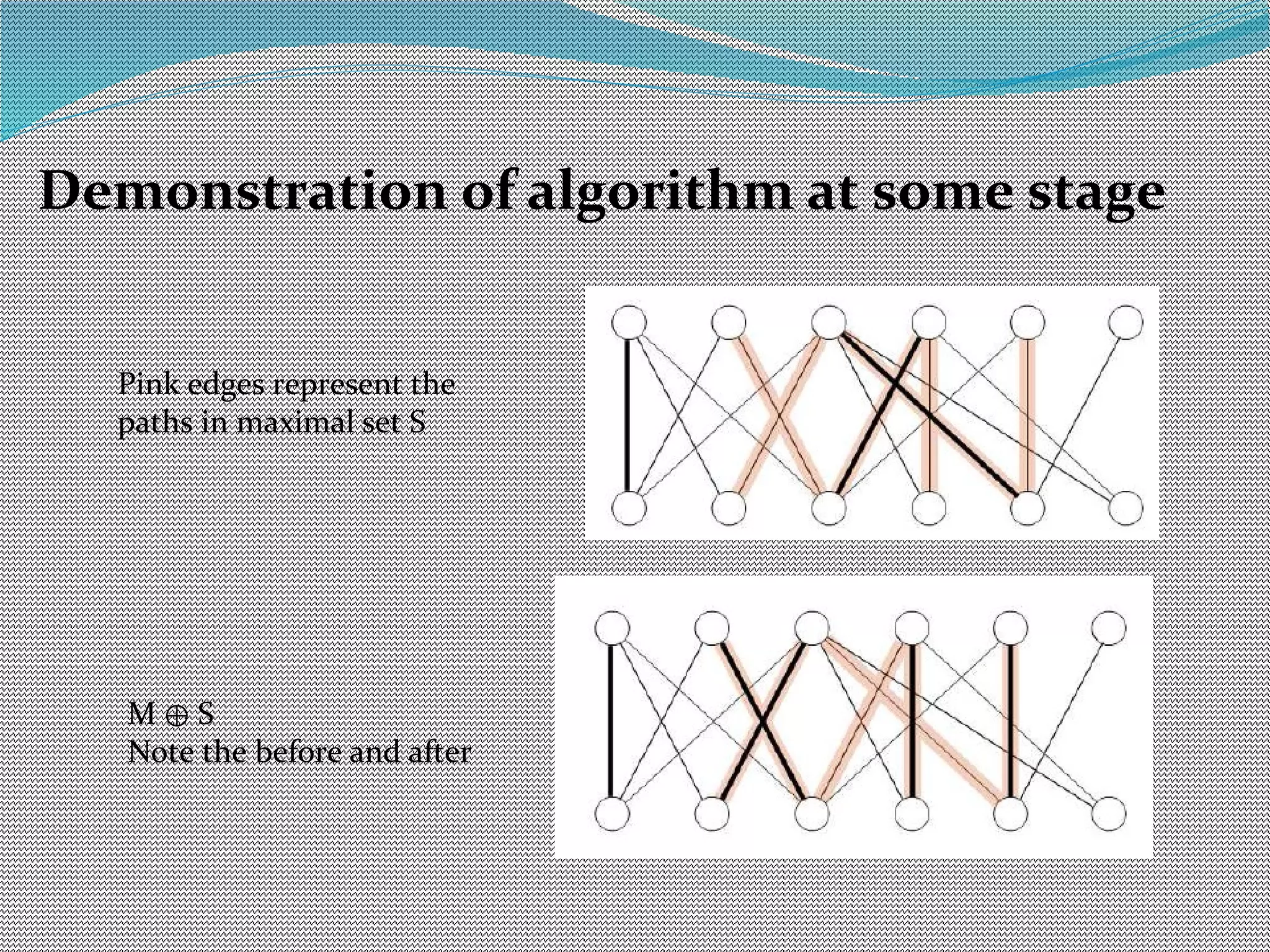
The document discusses algorithms for maximum matchings in bipartite graphs. It defines bipartite graphs and matchings. A simple algorithm finds augmenting paths and increments the matching size in each iteration, having complexity O(VE). The more efficient Hopcroft-Karp algorithm finds a maximal set of shortest augmenting paths and augments along all paths simultaneously in each iteration, achieving complexity O(√V√E). It demonstrates the algorithm augmenting the matching by alternating along paths in the maximal set.

1. Combinatorial Algorithms
(Algorithms in Bipartite Graphs)

2. Introduction
Algorithms in unweighted bipartite graph
Maximum matching
A simple algorithm
Hopcroft-Karp algorithm
Outline

3. Definition
A graph G = (V, E) is bipartite if there exists partition
V = X Y∪ with X Y =∩ ∅ and E X × Y⊆ .
Bipartite Graph types
Unweighted
Weighted
For every edge e E∈ , there is a
weight w(e) .
Introduction

4. Example:
There are a set of boys and a set of girls.
Each boy only likes girls and each girl only likes boys.
A common friend wants to match each boy with a girl such that
the boy and girl are both happy – but they both will only be
happy if the boy likes the girl and the girl likes the boy.
Is it possible for every situation?
Introduction
We can use a bipartite graph
to model this problem

5. Problem
Testing bipartiteness
Matching
Maximum matching problem
Introduction

6. Maximum matching

7. Definition
Matching
A Matching is a subset M E⊆ such that ∀v V∈ at most one
edge in M is incident upon v
– Maximum matching
– A Maximum Matching is matching M such that everyother
matching M′ satisfies |M′| ≤ |M|.
– Unweighted graph: |M|= the number of edges
– Weighted graph: |M|=
– Perfect Matching
– A matching which matches all vertices of the graph
Maximum matching

8. A Matching A Maximum MatchingNot a Matching
Definition
We say that a vertex is matched if it is incident to some edge in
M.
Otherwise, the vertex is free
matched
free
(not perfect)
Maximum matching

9. Definition
Alternating Paths
A path is alternating if its edges alternate
between M and E − M.
Augmenting Paths
An alternating path is augmenting if both
endpoints are free
Alternating Tree
A tree rooted at some free vertex v in
which every path is an alternating path.
• Alternating paths
( Y1, X2, Y2, X4 )
• Augmenting Path
(Y1, X2, Y2, X4, Y4, X5)
Maximum matching

10. Property of Augmenting Paths
Replacing the M edges by the E − M ones increments size of the
matching
(Path: Y1, X2, Y2, X4, Y4,
X5)
Berge's Theorem: A matching M is maximum iff it
has no augmenting path (Proof: Lec01 Page 3)
Maximum matching

11. A simple algorithm
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
Maximum matching

12. A simple algorithm
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
Maximum matching

13. A simple algorithm
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
Maximum matching

14. A simple algorithm
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
Maximum matching

15. A simple algorithm
• Commonly search algorithm (BFS, DFS) O(E)
• At most V times
• Complexity: O(VE)
X
2
X
3
X
1
Y
1
Y
2
Y
3
Y
4
Maximum matching

16. Hopcroft-Karp Algorithm
An algorithm to find the maximum matching given a
bipartite graph
Gordon

17. Introduction
• The Hopcroft-Karp algorithm was published in
1973
• It is a matching algorithm that finds a
maximum matching in bipartite graphs
• The main idea is to augment along a set of
vertex-disjoint shortest augment paths
simulatenously
• The complexity is O(√|V||E|)
• In this section, some Theorems and Lemmas
from graph theory will be stated without
showing the proof.

18. Definition
• We let the set A B denote the symmetric⊕
difference of the set
• A B = (A B) – (A B)⊕ ∪ ∩
• A maximal set of vertex-disjoint minimum
length augmenting path is defined as follows :
 It is a set of augmenting path
 No two path share a same vertex
 If the minimum length augmenting path is of
length k, then all paths in S are of length k
 If p is an augmenting path not in S, then p
shares a vertex with some path p’ in S

19. Algorithm
The algorithm of Hopcroft and Kraft is as follows :
Given a graph G = (X Y),E)∪
1) Let M = {} ,
2) Find S = {P1 , P2 , … Pk}
3) While S ≠ {}
M = M S⊕
Find S
4) Output M

20. Demonstration of algorithm at some stage
Let the dark edges represent the edges
in a matching M

21. Demonstration of algorithm at some stage
Pink edges represent an
augmenting path
Deleting them

22. Demonstration of algorithm at some stage
Another augmenting path
No more paths

23. Demonstration of algorithm at some stage
Pink edges represent the
paths in maximal set S
M S⊕
Note the before and after