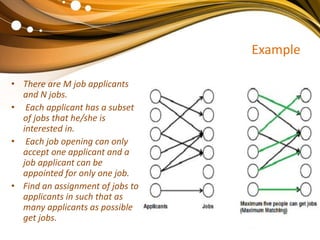
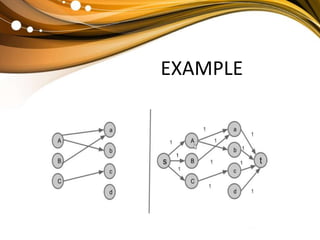
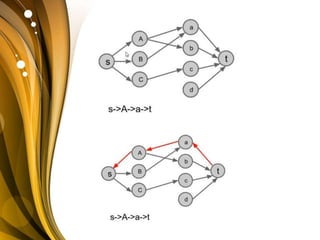
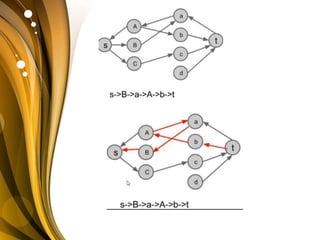
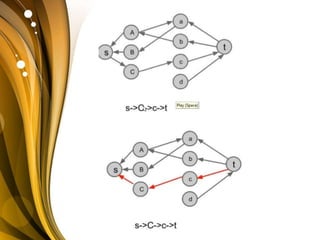
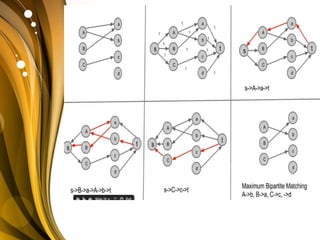
The document discusses the bipartite matching problem. It defines a bipartite graph as a graph whose vertices can be divided into two disjoint sets such that edges only connect vertices in different sets. A matching in a bipartite graph is a set of edges with no shared endpoints. The goal is to find a maximum matching, which is a matching with the greatest possible number of edges such that adding any other edge would violate the matching criteria. An example of this problem is matching job applicants to jobs where each applicant can be assigned only one job and each job only one applicant.

1. BIPARTITE
MATCHING PROBLEM
Prepared by
GEETHU RANGAN
MTECH TECHNOLOGY MANAGEMENT
DEPT OF FUTURE STUDIES
UNIVERSITY OF KERALA

2. Bipartite Matching
• A matching in a Bipartite Graph is a set of the
edges chosen in such a way that no two edges
share an endpoint.
• A maximum matching is a matching of maximum
size (maximum number of edges).
• In other words, a matching is maximum if any
edge is added to it, it is no longer a matching.
There can be more than one maximum
matchings for a given Bipartite Graph.

3. Example
• There are M job applicants
and N jobs.
• Each applicant has a subset
of jobs that he/she is
interested in.
• Each job opening can only
accept one applicant and a
job applicant can be
appointed for only one job.
• Find an assignment of jobs to
applicants in such that as
many applicants as possible
get jobs.

4. Bipartite Matching
• A Bipartite Graph G = (V,E) is a
graph in which the vertex set V
can be divided into two disjoint
subsets X and Y such that every
edge e ६ E has one end point in
X and the other end point in Y .
• A matching M is a subset of
edges such that each node in V
appears in at most one edge in
M.

7. EXAMPLE

12. THANK YOU