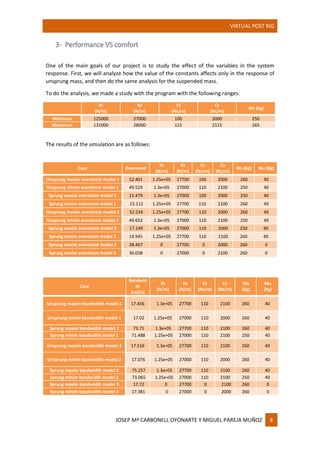
This document describes the development and implementation of a virtual suspension analysis system called the Virtual Post Rig. The system aims to analyze and characterize suspension parameters and response through computer simulation, providing advantages over physical testing such as lower cost and faster experimentation. The system models the vehicle suspension using different levels of simplification. It obtains transfer functions relating sprung and unsprung mass response to road inputs. These are used to calculate performance metrics and compare suspension designs, balancing performance and comfort factors.

1. VIRTUAL POST RIG
Mathematics and computing engineering
Development and implementation of a suspension
analysis system
Josep Mª Carbonell Oyonarte y Miguel
Pareja Muñoz
ETSEIAT-UPC

2. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 1
Contents
1- Introduction .......................................................................................................................... 2
1.1- Simplifications ............................................................................................................... 3
1.2- Modelization ................................................................................................................. 3
1.3- Goals.............................................................................................................................. 5
2- Program................................................................................................................................. 6
2.1- Theoretical approach......................................................................................................... 6
2.2- Performance Index............................................................................................................. 7
3- Performance VS comfort....................................................................................................... 8
3.1- Performance....................................................................................................................... 9
3.2- Comfort............................................................................................................................ 10
4- Model validation ................................................................................................................. 11
5- Acknowledgements............................................................................................................. 14
6- Literature............................................................................................................................. 15

3. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 2
1- Introduction
This project arises from the need to analyze and characterize the parameters and response of
a suspension system of a vehicle. Currently it is imperative to have a vision of the system and
in order to get it, there are plenty of facilities "Post Rig", a mechanism which transmits
vibrations to the vehicle and a sensor system monitors its response. These facilities have a set
of advantages and disadvantages:
Instead, what we propose is the creation of a virtual system in which, from the parameters of
the desired vehicle and the desired input, the temporary and frequency response of the
vehicle is obtained, where we can see the most important features. This improves both actual
Rig Post disadvantages discussed above:
 It is very economical. Only the computational power required by the program is
needed.
 It is extremely fast, being able to obtain system responses varying any parameter in a
simulation.
We obviously have the disadvantage that we are no longer working on the real car, but on a
simulation, where a number of simplifications and idealizations that we will discuss below have
been made.
Pros
• It works directly on the
vehicle. Therefore, there
are no modeling or
simplification errors.
Cons
• It is extremely expensive,
being a method available
to very few companies.
• Few set up variations.
During the time that last
test, you can make a few
changes in the system
parameters because they
are time consuming.

4. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 3
1.1- Simplifications
As we only want to study the vertical response of the vehicle, we use the model called ¼. This
means that the system is treated as if it were only connected to the ground by one point, and
the entire mass rests on a suspension. This simplification prevents obtaining the
characterization of the longitudinal and lateral movements, outside our goal.
We do not consider the suspension geometry, it would be impossible to introduce to the
program the lots of existing different geometries.
1.2- Modelization
Model 1
For our program we have decided to rely on the most accurate and most used academically
model. It is as follows:
We see that in this case we model the tire as a spring + shock set, because from academic
studies to date is the model that has a response more similar to the actual tire.

5. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 4
We have set out to assess the validity of two models more:
Model 2
In this model, also commonly used, the tire is modeled as a spring only. It is as follows:
Model 3
This is the most basic model. Hardly used in industry or in academic studies, only
educationally. It is as follows:

6. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 5
1.3- Goals
 Get both temporary and frequency response of a given suspension system. To study
their behavior.
 To study the influence of all parameters in the response of the suspension system of a
vehicle.
 To study the validity of the different possible models of suspension.
 Performance Index calculation of assessing the quality of the suspension.

7. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 6
2- Program
2.1- Theoretical approach
We have obtained the transfer functions of the system, i.e., the relationship between the
vertical response of the suspended mass (car) or the unsprung mass (absorber) versus soil
variation laying move the car.
To do this, we extracted the dynamics equations for each of the models discussed above.
After, we have passed from the time domain to the frequency domain using Laplace
transforms and finally obtained the transfer function of the system.
Then the process followed for the model 1, displayed in Figure 1, is shown, by way of example:
𝑀𝑠 𝑧̈ 𝑠 − 𝐶𝑠(𝑧𝑠̇ − 𝑧 𝑢̇ ) − 𝐾𝑠(𝑧𝑠 − 𝑧 𝑢) = 0
𝑀 𝑢 𝑧̈ 𝑢 − 𝐶𝑠(𝑧 𝑢̇ − 𝑧𝑠̇ ) − 𝐾𝑠(𝑧 𝑢 − 𝑧𝑠) + 𝐾𝑡(𝑧 𝑢 − 𝑧 𝑔) + 𝐶𝑡(𝑧 𝑢̇ − 𝑧 𝑔̇ ) = 0
𝑍𝑠 𝑀𝑠 𝑠2
− 𝐶𝑠 𝑠(𝑍𝑠 − 𝑍 𝑢) − 𝐾𝑠(𝑍𝑠 − 𝑍 𝑢) = 0
𝑍 𝑢 𝑀 𝑢 𝑠2
− 𝐶𝑠 𝑠(𝑍 𝑢 − 𝑍𝑠) − 𝐾𝑠(𝑍 𝑢 − 𝑍𝑠) + 𝐾𝑡(𝑍 𝑢 − 𝑍 𝑔) + 𝐶𝑡 𝑠(𝑍 𝑢 − 𝑍 𝑔) = 0
 Unsprung mass versus ground
𝑍 𝑢
𝑍 𝑔
(𝑠) =
𝐶𝑠 𝐶𝑡 𝑠2
+ (𝐾𝑡 𝐶𝑠 + 𝐾𝑠 𝐶𝑡)𝑠 + 𝐾𝑡 𝐾𝑠
𝑀 𝑢 𝑀𝑠 𝑠4 + (𝑀𝑠 𝐶𝑡 + 𝐶𝑠(𝑀 𝑢 + 𝑀𝑠))𝑠3 + (𝐾𝑠(𝑀 𝑢 + 𝑀𝑠) + 𝐾𝑡 𝑀𝑠 + 𝐶𝑠 𝐶𝑡)𝑠2 + (𝐾𝑡 𝐶𝑠 + 𝐾𝑠 𝐶𝑡)𝑠 + 𝐾𝑡 𝐾𝑠
 Sprung mass versus ground
𝑍𝑠
𝑍 𝑔
(𝑠) =
𝑀𝑠 𝐶 𝑡 𝑠3+(𝐶 𝑡 𝐶 𝑠+𝐾𝑡 𝑀𝑠)𝑠2+(𝐾𝑡 𝐶 𝑠+𝐾𝑠 𝐶𝑡)𝑠+𝐾𝑡 𝐾𝑠
𝑀 𝑢 𝑀𝑠 𝑠4+(𝑀𝑠 𝐶 𝑡+𝐶 𝑠(𝑀 𝑢+𝑀𝑠))𝑠3+(𝐾𝑠(𝑀 𝑢+𝑀𝑠)+𝐾𝑡 𝑀𝑠+𝐶 𝑠 𝐶 𝑡)𝑠2+(𝐾𝑡 𝐶 𝑠+𝐾𝑠 𝐶𝑡)𝑠+𝐾𝑡 𝐾𝑠
Dynamics equations
(time domain)
Dynamics equations
(frequency domain,
because s=jw)
Laplace transforms

8. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 7
Overshoot
This value is the maximum value of the response to a step input less the end value of the
stabilized response, divided by the final value.
Bandwidth
This value is the frequency at which the response has a gain of about -3dB regarding the gain
at very low frequencies.
Steady state error
This value is the difference between the response of the system and the entrance to it, once
passed the transition period of stabilization.
.
2.2- Performance Index
We defined this value as the sum of distances from the response of the unsprung mass to an
input impulse regarding ground divided by the number of points assessed.
This parameter provides an assessment of the quality of the system, being higher as smaller
this value. In this way, we can compare two completely different suspensions just by looking at
this value.

9. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 8
3- Performance VS comfort
One of the main goals of our project is to study the effect of the variables in the system
response. First, we will analyze how the value of the constants affects only in the response of
unsprung mass, and then do the same analysis for the suspended mass.
To do the analysis, we made a study with the program with the following ranges:
Kt
(N/m)
Ks
(N/m)
Ct
(Ns/m)
Cs
(Ns/m)
Ms (Kg)
Minimum 125000 27000 100 2000 250
Maximum 131000 28000 115 2115 265
The results of the simulation are as follows:
Case Overshoot
Kt
(N/m)
Ks
(N/m)
Ct
(Ns/m)
Cs
(Ns/m)
Ms (Kg) Mu (Kg)
Unsprung maxim overshoot model 1 52.401 1.25e+05 27700 100 2000 260 40
Unsprung minim overshoot model 1 49.529 1.3e+05 27000 110 2100 250 40
Sprung maxim overshoot model 1 15.479 1.3e+05 27000 100 2000 250 40
Sprung minim overshoot model 1 13.112 1.25e+05 27700 110 2100 260 40
Unsprung maxim overshoot model 2 52.534 1.25e+05 27700 110 2000 260 40
Unsprung minim overshoot model 2 49.652 1.3e+05 27000 110 2100 250 40
Sprung maxim overshoot model 2 17.249 1.3e+05 27000 110 2000 250 40
Sprung minim overshoot model 2 14.945 1.25e+05 27700 110 2100 260 40
Sprung maxim overshoot model 3 38.467 0 27700 0 2000 260 0
Sprung minim overshoot model 3 36.038 0 27000 0 2100 260 0
Case
Bandwid
th
(rad/s)
Kt
(N/m)
Ks
(N/m)
Ct
(Ns/m)
Cs
(Ns/m)
Ms
(Kg)
Mu
(Kg)
Unsprung maxim bandwidth model 1 17.456 1.3e+05 27700 110 2100 260 40
Unsprung minim bandwidth model 1 17.02 1.25e+05 27000 110 2000 260 40
Sprung maxim bandwidth model 1 73.71 1.3e+05 27700 110 2100 260 40
Sprung minim bandwidth model 1 71.488 1.25e+05 27000 110 2100 250 40
Unsprung maxim bandwidth model 2 17.516 1.3e+05 27700 110 2100 260 40
Unsprung minim bandwidth model 2 17.076 1.25e+05 27000 110 2000 260 40
Sprung maxim bandwidth model 2 75.257 1.3e+05 27700 110 2100 260 40
Sprung minim bandwidth model 2 73.065 1.25e+05 27000 110 2100 250 40
Sprung maxim bandwidth model 3 17.72 0 27700 0 2100 260 0
Sprung minim bandwidth model 3 17.381 0 27000 0 2000 260 0

10. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 9
The optimum values for the system to be analyzed are small Overshoot and large Bandwidth.
This will produce a low amplitude response and quickly eliminate oscillation.
If we want to maximize vehicle performance, we must optimize the response of the unsprung
mass, because we are interested in the tire contact as long as possible. But if we study the
vehicle's comfort, we optimize the response of the suspended mass, seeking to obtain the
smallest possible oscillation.
3.1- Performance
For unsprung mass, we can evaluate the Overshoot decreases when:
 Kt, that is, hardness of the tire increases.
 Ks, that is, hardness of the spring decreases.
 Ct
 Cs
 Ms
As for the Bandwidth, this increases when:
 Kt
 Ks
 Ct
So in terms of optimize the performance, we use hard tires, shock absorbers with a great Cs,
and reduce to a minimum the suspended mass. Regarding the spring rate, high hardness
observed that provoke a larger Overshoot, but also increase the speed of dissipation. We
should study each case.
We present the graphs of the response of the unsprung mass of model 1 obtained with the
program:

11. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 10
3.2- Comfort
When we look at the suspended mass, we note that to decrease the Overshoot must:
 Kt
 Ks
 Ct
 Cs
 Ms
And to increase the Bandwidth we must:
 Kt
 Ks
 Ct
 Ms
We found that there is difference between the response of the sprung mass and unsprung. If
we want to optimize comfort, we assemble a stiffer springs, dampers with high Cs, increase
suspended mass, and particularly assess the choice between soft and hard tires.
Finally, to get a clearer idea of the system response, we present the graphs of the suspended
mass obtained from Model 1 with the program:

12. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 11
4- Model validation
At the beginning of our program, we have taken as reference the most exhaustive ¼ vehicle
model. This is because most accurate studies use it, but we set as one of the objectives to
assess the accuracy of the assumptions and simplifications done in the other two models
studied. To do this, our program takes all graphics for each model, so you can make a visual
assessment of the differences in the response of each, and also calculate the error in the
values of maximum Overshoot and minimum Bandwidth (as they are the most damaging for
the system) committed by models 2 and 3. Presenting the values obtained in the previous
simulation:
Model Bandwidth Error Overshoot Error
Model 2 2.2054 11.44
Model 3 75.686 148.51
As we can see, the model 2 is acceptable in calculating the Bandwidth, because it has a
2.2054% error regarding the value obtained with the model 1, but differs much more on the
maximum Overshoot.
Model 3 presents a big mistake in calculating the Bandwidth minimum, but it is absolutely
useless to calculate the Overshoot.
Here are the graphs obtained for each model, to make a visual recognition of differences in the
response:
UNSPRUNG MASS
SPRUNG MASS

13. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 12
As a conclusion, we can safely say that the model 3 is totally useless to make a minimally
serious study of the system, since it has some mistakes too high.

14. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 13
As for the model 2, we see that the differences are not so great. We should make an
assessment in each individual case whether it is advantageous to win the precision you get
with Model 1, or if that is more advantageous to sacrifice precision in order to get a lower
complexity and computation time by eliminating the tire damper, using model 2.

15. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 14
5- Acknowledgements
We want to finish the project by thanking all the help provided by Prof. Joseba Quevedo. It has
always been open to any consultation, encouraging us to get a job where you meet our goals
one step beyond our comfort zone.

16. VIRTUAL POST RIG
JOSEP Mª CARBONELL OYONARTE Y MIGUEL PAREJA MUÑOZ 15
6- Literature
 Estudio del comportamiento dinámico de un vehículo utilizando la herramienta
simmechanics de Matlab; Iván Mula, Universidad Carlos III de Madrid.
 Comandos de Matlab útiles para la asignatura de Control; Analía Pérez Hidalgo;
Universidad Nacional de San Juan.
 Los Sistemas de Suspensión Activa y Semiactiva: Una Revisión; Jorge Hurel Ezeta,
Anthony Mandow, Alfonso García Cerezo; Revista Iberoamericana de Automática e
Informática industrial.
 Aerodinámica y Aero Post Rig aplicados al Diseño de Coches de Competicion; Timoteo
Briet