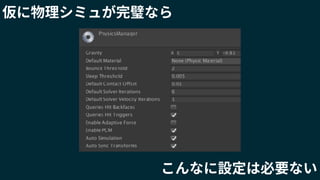
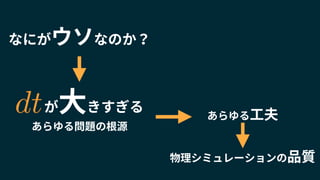
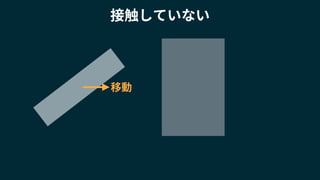
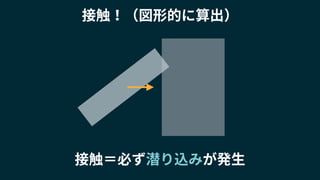
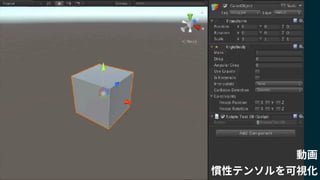
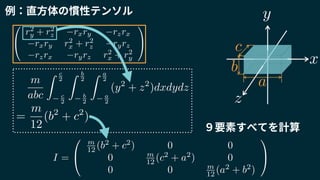
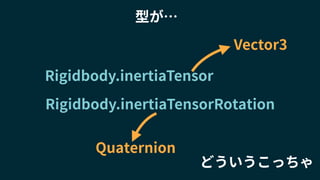
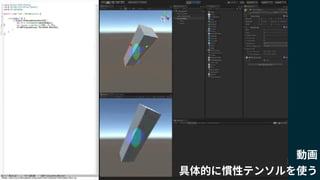
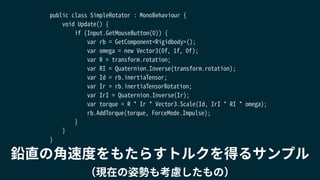
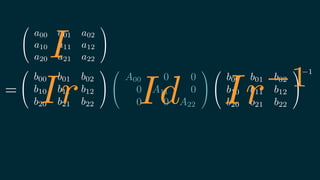2018/1/25に開催されたUnity道場 物理シミュレーション完全マスター の講演スライドです。
講師:安原 祐二( ユニティ・テクノロジーズ・ジャパン合同会社 )
ゲームのみならず様々なアプリケーションにおいて、物理挙動の導入は品質の向上や開発の効率化につながります。Unityに搭載されている物理シミュレーションはたいへん優れたもので、その原理を理解することでより一層表現力が高まるでしょう。この講演では、物理の初歩を丁寧に解説しつつ、プロの現場で応用されるテクニックについてお話しします。
こんな人にオススメ
・UnityでRigidbodyを使用したことのあるプログラマ
・物理シミュレーションの概観を知りたい方
得られる知見
・コンピュータにおける物理シミュレーションの原理
・物理シミュレーションを扱う上での注意点
・物理シミュレーションの具体的な応用例
関連動画:
[Unity道場 札幌スペシャル]プロが教える脱初心者スクリプト術!
https://youtu.be/FqjM9oujyNE
Unityのイベント資料はこちらから:
https://www.slideshare.net/UnityTechnologiesJapan/clipboards




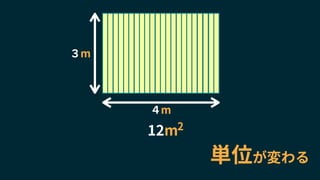




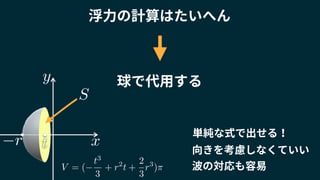
![例:球の体積(部分)
r
S
t
V =
Z t
r
Sdx
=
Z t
r
⇡(r2
x2
)dx
= ⇡[r2
x
x3
3
]t
r
= ⇡{r2
t
t3
3
( r2
r
r3
3
)}
= (
t3
3
+ r2
t +
2
3
r3
)⇡
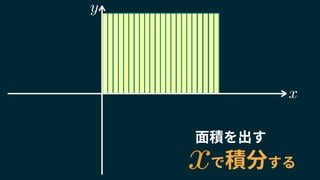
円の面積を重ねる
呪文
理解
x
y](https://image.slidesharecdn.com/20180125-180124100216/85/Unity-17-320.jpg)


































![指定終端速度 を得るための外力
[Unity]RigidbodyのDragから終端速度を得る
https://qiita.com/yuji_yasuhara/items/1f438f0f27f5ef854a73参
考
:質量
:Drag
m
k
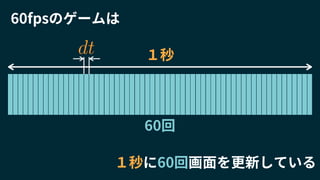
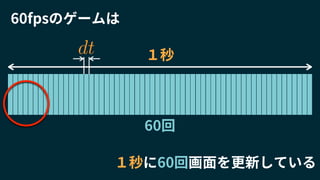
F =
1 dt
vmk
k
v F](https://image.slidesharecdn.com/20180125-180124100216/85/Unity-70-320.jpg)
![〜実践的な物理入門〜
https://www.youtube.com/watch?v=FqjM9oujyNE
[Unity道場 札幌スペシャル]
プロが教える脱初心者スクリプト術!
参
考](https://image.slidesharecdn.com/20180125-180124100216/85/Unity-71-320.jpg)