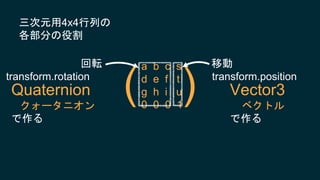
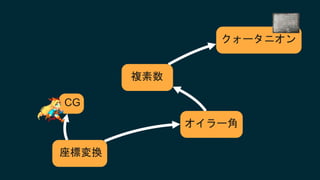
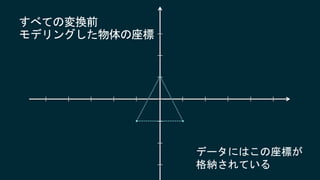
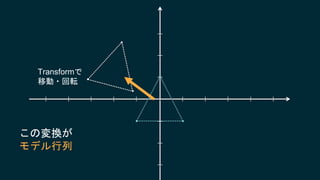
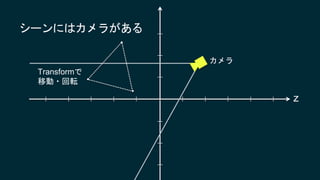
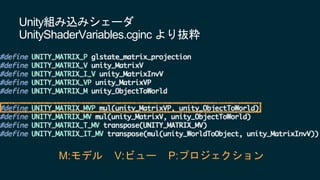
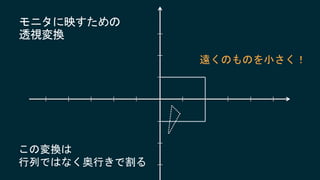
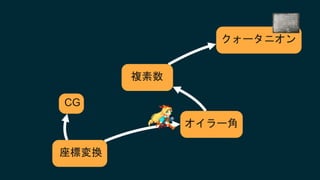
2017/6/3に開催されたUnity道場 博多スペシャルの講演スライドです。
講師:安原 祐二(ユニティ・テクノロジーズ・ジャパン合同会社)
講演動画:https://youtu.be/uKWLPU8gfIY
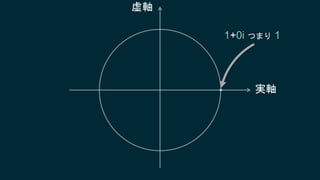
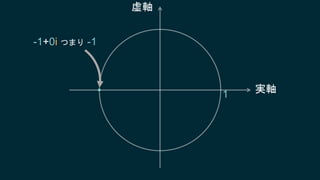
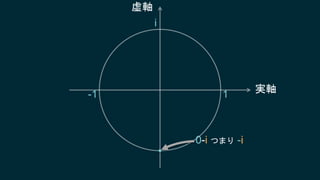
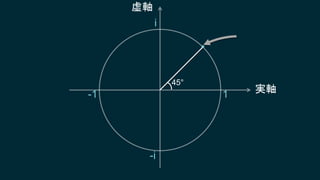
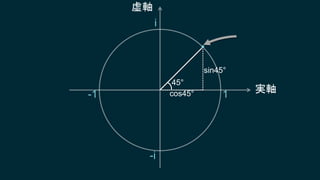
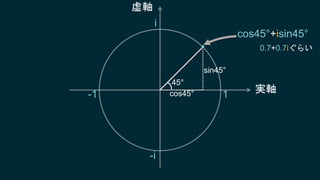
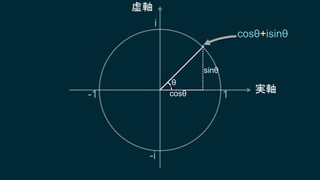
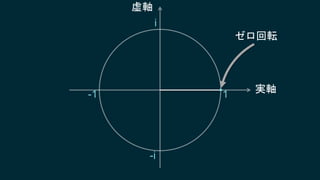
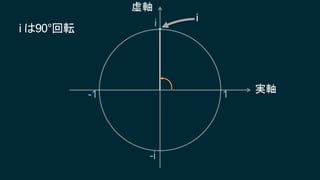
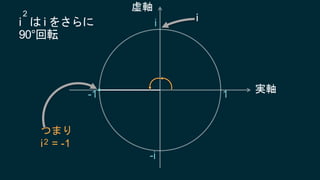
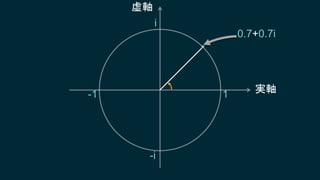
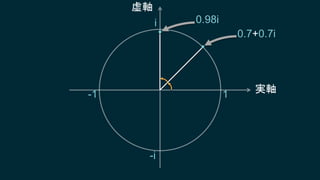
知ってはいるけれどピンとこない、知ってはいるけれどピンとこない、そんなクォータニオンについて基本となる概念からたっぷりと、丁寧に説明していきます。行列についても解説しますので、これからシェーダプログラミングに取り組もうとするエンジニアにも役に立つ内容です。数学に苦手意識のある人も、この機会にマスターしてしまいましょう!
こんな人におすすめ
・プログラマ全般および数学に興味のある人
受講者が得られる知見
・クォータニオンの意味
・行列とクォータニオンの関係
・数学的な背景
Unityのイベント資料はこちらから:
https://www.slideshare.net/UnityTechnologiesJapan/clipboards


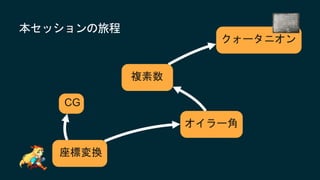



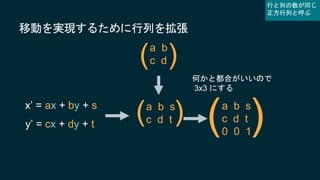
![こういう式にしてみよう
x’ = ax + by
y’ = cx + dy
P’(x’, y’) = [変換]P(x, y)](https://image.slidesharecdn.com/unity-yasuhara-170616125618/85/Unity-2017-10-320.jpg)



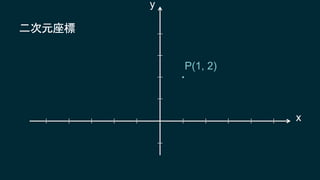
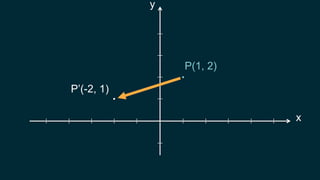
![変換を行列Mとして
P(1, 2) P’(-2, 1)
変換
P’=MP
P’(x’, y’) = [変換]P(x, y)](https://image.slidesharecdn.com/unity-yasuhara-170616125618/85/Unity-2017-14-320.jpg)
![a b
c d( )P’= P
変換を行列Mとして
P(1, 2) P’(-2, 1)
変換
P’=MP
P’(x’, y’) = [変換]P(x, y)](https://image.slidesharecdn.com/unity-yasuhara-170616125618/85/Unity-2017-15-320.jpg)