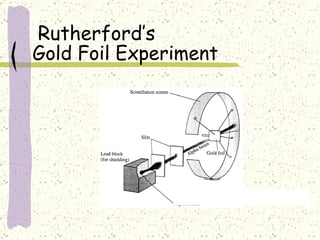
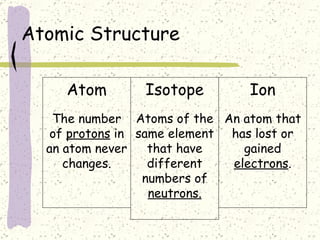
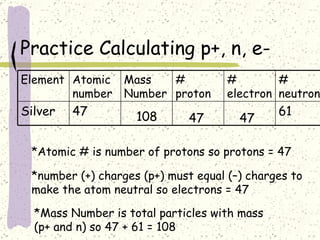
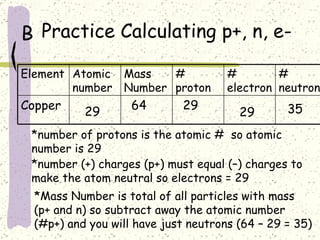
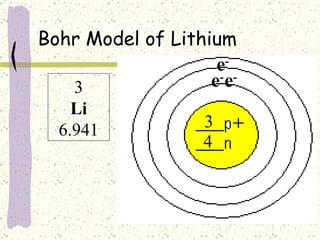
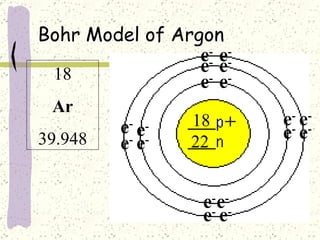
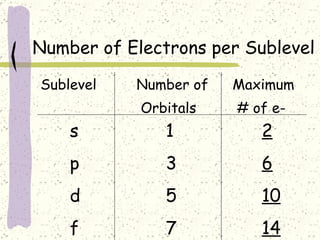
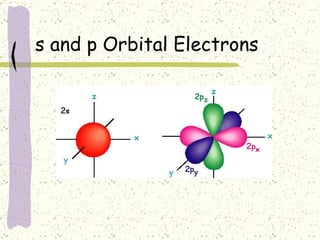
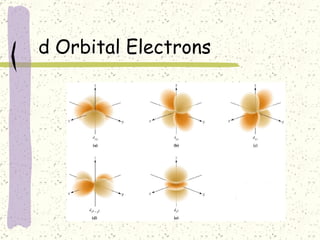
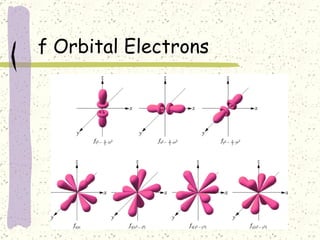
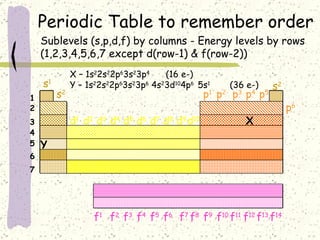
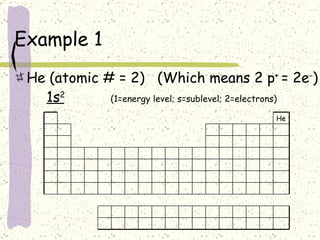
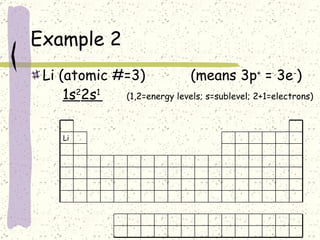
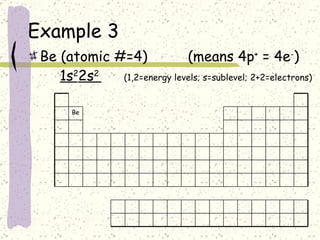
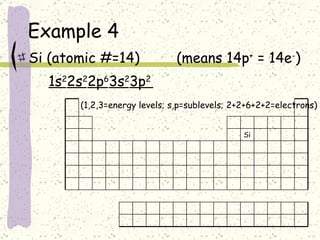
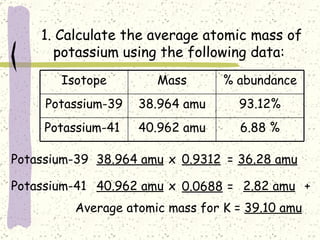
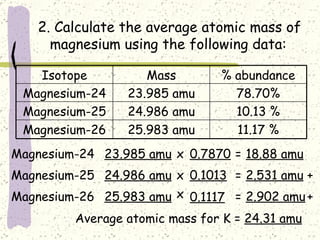
This document provides a brief history of the atomic theory, from early philosophers' ideas to the modern quantum model. It describes Democritus' idea of indivisible atoms, Dalton's model of atoms as solid spheres, Thomson's discovery of electrons, Rutherford's gold foil experiment showing the nucleus, Bohr's planetary model, and the modern electron cloud/quantum model with protons and neutrons in the nucleus and electrons in clouds outside. It also discusses atomic structure, isotopes, ions, atomic mass, and calculating atomic properties using atomic number and mass number.

1. Chemistry Unit Three Atomic Structure

2. A Brief History of the Atomic Theory

3. Democritus 400 B.C. Greek philosopher Coined the term “atomos” which means, Indivisible . All matter is made of atoms. Atoms are hard , solid particles , made of the same material but are of different shapes and sizes.

4. John Dalton 1803 English Chemist Atoms are solid , neutral spheres. Atoms of same element are the same . Atoms of different elements are different . Compounds form from the joining of atoms of two or more elements.

5. J.J. Thomson 1897 English Chemist. Atoms are made of even smaller particles . Called the Plum Pudding Model ( Chocolate Chip Cookie Dough Model ) Positively charged material through which negative particles are scattered. Since atoms are neutral , therefore, there must be (+) particles too, but Thomson never found them . Cathode Ray Experiments; discovered the electron.

6. Ernest Rutherford 1911 British physicist Gold Foil experiment. Atom has a small, dense positively charged center called the Nucleus . Negative electrons are scattered outside the nucleus. Most of the atom is empty space If an atom was the size of a baseball stadium, the nucleus would be the size of a marble . .

7. Gold Foil Experiment Rutherford’s

8. A beam of + particles (alpha particles) shot through a thin sheet of gold foil. Most particles passed straight through. (Most of atom is empty space.) A few were deflected. (Positive core-similar charges repel each other.) Very few bounced off. (Solid core is very small.)

9. Neils Bohr 1913 Danish Scientist Planetary model. Electrons are held in place by the attraction between them and the + charged nucleus. Each electron occupies a specific energy level and orbit the nucleus like planets circling the sun. Labeled each energy level by a quantum number.

10. Electrons are not discreet particles moving in discreet orbits. The probable location of an electron depends on how much energy it has. Electrons seem to be everywhere at once, like the moving blades of a fan. Wave Model

11. Electron Cloud Model Positively charged protons and neutral neutrons are held together with a huge amount of energy forming the nucleus of the atom. Negatively charged electrons move rapidly around the outside of the nucleus forming “clouds” of negative charge . Most of the mass of the atom is in the nucleus. Quantum Model

12. Atomic Structure Found in the Nucleus Found in the Nucleus Found outside the nucleus Has 1 amu of mass Has 1 amu of mass Has 0 amu of mass Has a positive charge Has a negative charge Has no charge (neutral) Electrons (e-) Neutrons (n) Protons (p+)

13. Atomic Structure Atom The number of protons in an atom never changes. Isotope Atoms of the same element that have different numbers of neutrons. Ion An atom that has lost or gained electrons .

14. Atomic Mass Average Atomic Mass – the average mass of all of the isotopes of an element. Decimal number. Mass Number – the total number of protons and neutrons in the nucleus of an atom. Whole number.

15. Atomic Structure Atomic Number = the number of protons . Equal to the number of electrons. Atomic Mass = the number of protons and neutrons added together . Atomic Mass – Atomic Number = the number of neutrons .

16. 6 C 12.011 Atomic Number = 6 6 protons = 6 electrons 6 p+ = 6 e- (atom is neutral) Atomic Mass = 12 12 p+ and n -6 p+ 6 neutrons Calculating Numbers of Protons, Neutrons and Electrons.

17. Practice Calculating p+, n, e- *Atomic # is number of protons so protons = 47 *number (+) charges (p+) must equal (–) charges to make the atom neutral so electrons = 47 *Mass Number is total particles with mass (p+ and n) so 47 + 61 = 108 47 47 108 61 47 Silver # neutron # electron # proton Mass Number Atomic number Element

18. B Practice Calculating p+, n, e- *number of protons is the atomic # so atomic number is 29 *number (+) charges (p+) must equal (–) charges to make the atom neutral so electrons = 29 *Mass Number is total of all particles with mass (p+ and n) so subtract away the atomic number (#p+) and you will have just neutrons (64 – 29 = 35) 35 29 29 29 64 Copper # neutron # electron # proton Mass Number Atomic number Element

19. Practice Calculating p+, n, e- Remember  e- = p+ (to make atom neutral)  #p+ is atomic number  p+ + n = mass number  Mass number – atomic number = n 50 50 119 2 2 2 5 5 5 Is # p+ + = - (neutral) + = - (neutral) p + + n Is # p+ Mass # - atomic # Mass #- n + = - (neutral) Is # p+ 6 11 Boron 2 4 Helium 69 50 Tin # neutron # electron # proton Mass Number Atomic number Element

20. Bohr Models p + & n in nucleus e - in energy levels around nucleus 3 energy levels -1 st has up to 2e - -2 nd has up to 8e - -3 rd has up to 8e - e - e - e - e - e - e - e - e - e - e - e - e - e - e - e - e - e - e -

21. Bohr Model of Lithium 3 4 e - e - e - 3 Li 6.941

22. Bohr Model of Argon 18 22 e - e - e - 18 Ar 39.948 e - e - e - e - e - e - e - e - e - e - e - e - e - e - e -

23. Electron Configuration Shows the distribution of electrons among the orbitals of an atom. Describes where the electrons are located and how much energy each one has.

24. Rules for Electron Configuration Aufbau Principle - Electrons enter orbitals of lowest energy level first. Pauli Exclusion Principle – An orbital can hold a maximum of 2 electrons. To occupy the same orbital, the 2 electrons must spin in opposite directions. Hund’s Rule - one electron enters each orbital until each orbital contain one electron with parallel spins before a second electron is added.

25. Determining Electron Configurations Quantum Numbers describe the amount of energy in that level. The lower the number, the less energy it has. (n = 1, 2, 3, 4, etc.) Sublevels are divisions of the principle energy levels. The main sublevels are called s , p , d and f . Each sublevel has a different shape caused by the different energy levels.

26. Number of Electrons per Sublevel Sublevel Number of Maximum Orbitals # of e- s 1 2 p 3 6 d 5 10 f 7 14

27. s and p Orbital Electrons

28. d Orbital Electrons

29. f Orbital Electrons

30. Periodic Table to remember order s 1 s 2 s 2 p 1 p 2 p 3 p 4 p 5 p 6 d 1 d 2 d 3 d 4 d 5 d 6 d 7 d 8 d 9 d 10 f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 f 10 f 11 f 12 f 13 f 14 Sublevels (s,p,d,f) by columns - Energy levels by rows (1,2,3,4,5,6,7 except d(row-1) & f(row-2)) 1 2 3 4 5 6 7 X – 1s 2 2s 2 2p 6 3s 2 3p 4 (16 e-) Y – 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5s 1 (36 e-) X Y

31. Example 1 He (atomic # = 2) (Which means 2 p + = 2e - ) 1s 2 (1=energy level; s=sublevel; 2=electrons) He

32. Example 2 Li (atomic #=3) (means 3p + = 3e - ) 1s 2 2s 1 (1,2=energy levels; s=sublevel; 2+1=electrons) Li

33. Example 3 Be (atomic #=4) (means 4p + = 4e - ) 1s 2 2s 2 (1,2=energy levels; s=sublevel; 2+2=electrons) Be

34. Example 4 Si (atomic #=14) (means 14p + = 14e - ) 1s 2 2s 2 2p 6 3s 2 3p 2 (1,2,3=energy levels; s,p=sublevels; 2+2+6+2+2=electrons) Si

35. Lewis Dot Structures One more type of atomic model… (In addition to Bohr models and electron configurations) Consists of the element’s symbol and the atom’s valence electrons. Symbol = kernel (represents the protons, neutrons and full electron shells). Dots = valence electrons.

36. Lewis Dot Structures Con’t B B = Kernel (The protons, neutrons and full electron shells.) Valence shell electrons

37. You can use the Electron Configuration to get the Lewis Dot Structure… Ca 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 Locate the highest quantum number. (4) Add the s and p orbital electrons, and place them around the element symbol. (2) Ca

38. One Final Example Tin 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 6 5s 2 4d 10 5p 2 Locate the highest quantum number (5) Add the s and p orbital electrons (4) Sn

39. How to place electrons on a Lewis Dot First two dots represent the s orbital electrons and are placed at the top of the element’s symbol. Then the p orbital electrons are placed in this order: right, bottom, left, right, bottom, left.

40. Ne 1 2 3 4 5 6 7 8 So, it goes like this…

41. Percent Abundance The percentage of how much one specific isotope of an element is found in nature. FORMULA: % abundance = amount of one isotope total amount of all isotopes

42. Average Atomic Mass (How the number ends up on the periodic table!!) 1 st  Mass of one isotope x % abundance in decimal form (watch SIG FIGS!!) 2 nd  Do this for each isotope of that element 3 rd  Then add all individual isotopes together to get the average atomic mass.

43. 1. Calculate the average atomic mass of potassium using the following data: Potassium-39 38.964 amu x 0.9312 = 36.28 amu Potassium-41 40.962 amu x 0.0688 2.82 amu = + Average atomic mass for K = 39.10 amu 6.88 % 40.962 amu Potassium-41 93.12% 38.964 amu Potassium-39 % abundance Mass Isotope

44. 2. Calculate the average atomic mass of magnesium using the following data: Magnesium-24 23.985 amu x 0.7870 = 18.88 amu Magnesium-25 24.986 amu x 0.1013 2.531 amu = + Average atomic mass for K = 24.31 amu + Magnesium-26 25.983 amu x 0.1117 = 2.902 amu 11.17 % 25.983 amu Magnesium-26 10.13 % 24.986 amu Magnesium-25 78.70% 23.985 amu Magnesium-24 % abundance Mass Isotope