This document introduces Reed-Solomon codes. It describes Reed-Solomon codes as word-oriented, non-binary BCH codes that are simple, robust, and perform well for burst errors. It explains that a Reed-Solomon code block length is N=2m-1, with a capacity to correct t errors using 2t parity check words. The document outlines the generator polynomial, encoding, decoding procedures including syndrome calculation, Berlekamp-Massey algorithm, Chien search, and Forney algorithm. It concludes with potential future tasks related to Reed-Solomon codes.

1. Introduction to
Reed-Solomon Code
Peng Xu
C5000 Software Development Group
Texas Instruments Inc.
Stafford, Texas

2. What is Reed-Solomon Code?
♦ Word-oriented non-binary BCH code
♦ Simplicity, Robustness and good
performance for burst errors
♦ Code block length N = 2 − 1
m
♦ t errors correcting capacity with 2t parity
check words
♦ Galois Field based coding technique

3. Generator Polynomial
♦ The generator polynomial determines the
properties of the code:
G(x) = (x −α m0 +1
)(x −α m0 +2
) (x −α m0 +2t
)
2t −1
= x + g2t−1x
2t
+ + g1x + g0x 0
where α is a primitive element of GF ( 2 m )
m0 is some integer usually set to 0

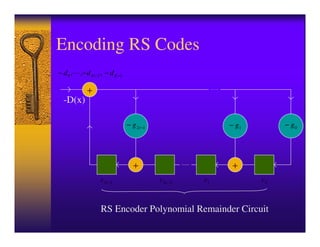
4. Encoding RS Codes
C ( x) = D( x) ⋅ x 2t − [ D( x) ⋅ x 2t mod G ( x)]
where C(x) is the transmitted codeword polynomial, of
degree N-1
D(x) is the user data polynomial, of degree K-1
G(x) is the generator polynomial of the code, of
degree 2t
and N – K = 2t
d K −1 d K − 2 d1 d0 c2t −1 c2t − 2 c1 c0
User Data Parity

5. Encoding RS Codes
− d0 , ,− d K − 2 , − d K −1
+
-D(x)
− g 2t −1 − g1 − g0
+ +
c2t −1 c2 t − 2 c1 c0
RS Encoder Polynomial Remainder Circuit

6. Decoding RS Codes
let R(x) = C(x) + E(x)
where R(x) is the received message polynomial with errors
C(x) is the transmitted correct codeword polynomial
E(x) is the unknown error polynomial
let S(x) = R(x) mod G(x) = E(x) mod G(x)
where S(x) is the syndrome of the received message
G(x) is the generator polynomial of the code

7. RS Decoding Procedure
1. Calculate Syndrome Ei = r(αi ) i = 0,1,...,2t −1
2. Calculate Error Locator Polynomial Λ (x)
using Berlekamp–Massey algorithm
3. Determine the roots of Λ (x) which are related
to the error locations using Chien Search
4. Calculate the coefficients of the error evaluator
polynomial Ω(x) using Forney Algorithm
5. Calculate the error magnitude
6. Recover the corrected codeword

8. Syndrome &
Error Locator polynomial
Syndrome Ei = r (α i ) i = 0,1,...,2t − 1
Error Locator polynomial v
Λ( x) = ∏ (1 − α ) = 1 + Λ1 x1 +
ljx
Λv xv
j =1
where the are the index of the errors
lj v
Et −1 E0 Λ1 Et
=
E2t −2 Et −1 Λ t E2t −1

9. Berlekamp-Massey Algorithm
This algorithm was developed by Berlekmap
and Massey to solve the problem of
determining the error locator polynomial.
It reduces the complexity from O(t 3 ) of
matrix inversion to O(t 2 ) .

10. Chien Search
Factoring the roots of the error locator
polynomial is typically done by evaluating
it at every point and testing to see if the
result is zero.
The Chien search is a way of doing this
which has a fairly regular structure.

11. Forney algorithm
Error Evaluator polynomial
E ( x)Λ( x) = Ω( x)( x n − 1)
Error Value
α k Ω(α − k )
ek =
Λ′(α −k )

12. Future Tasks
♦ More flexible generator polynomial?
♦ More Logarithm tables of GF?
♦ Convert C54x to C55x codes?
♦ Application Notes?
♦ More…