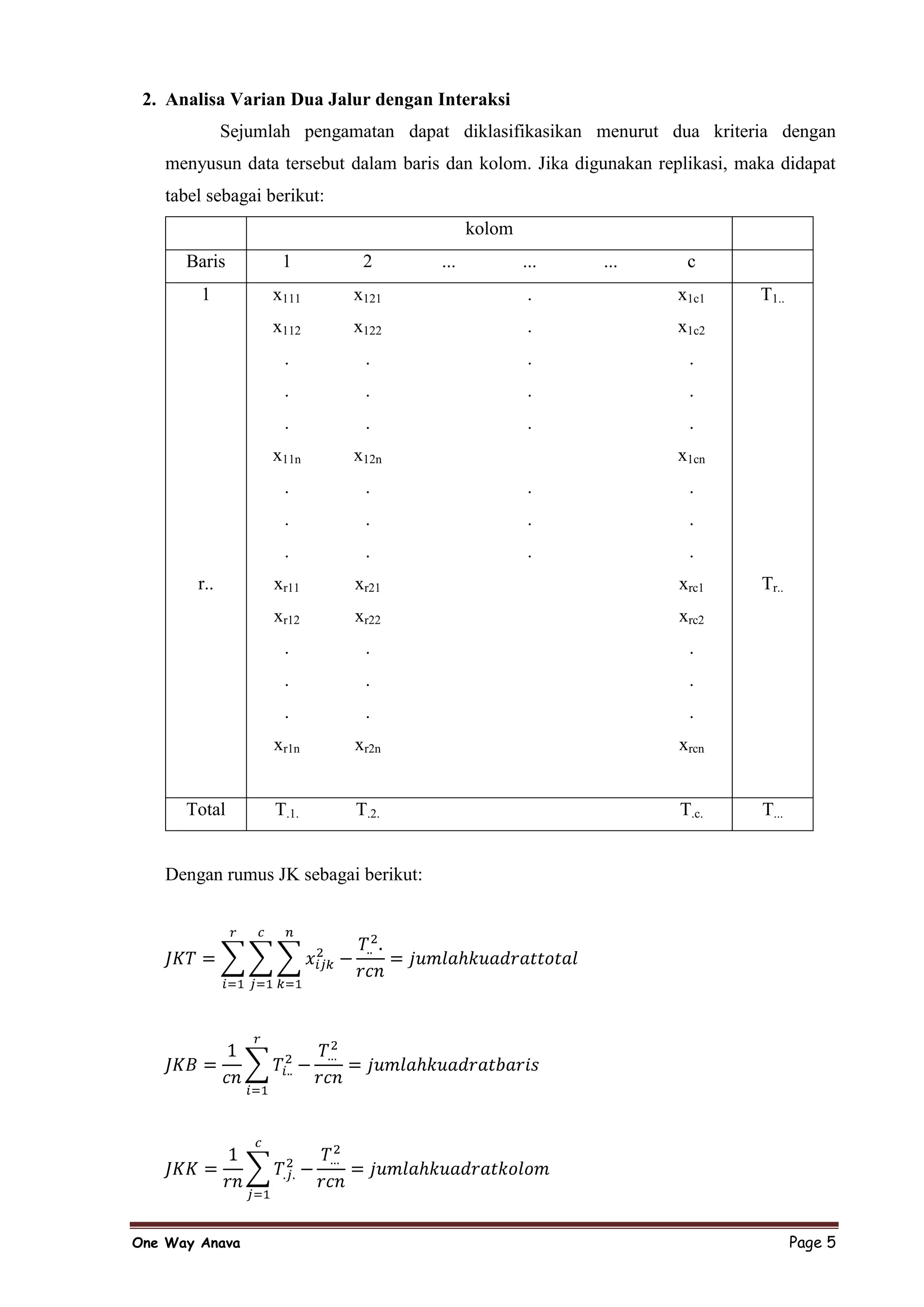
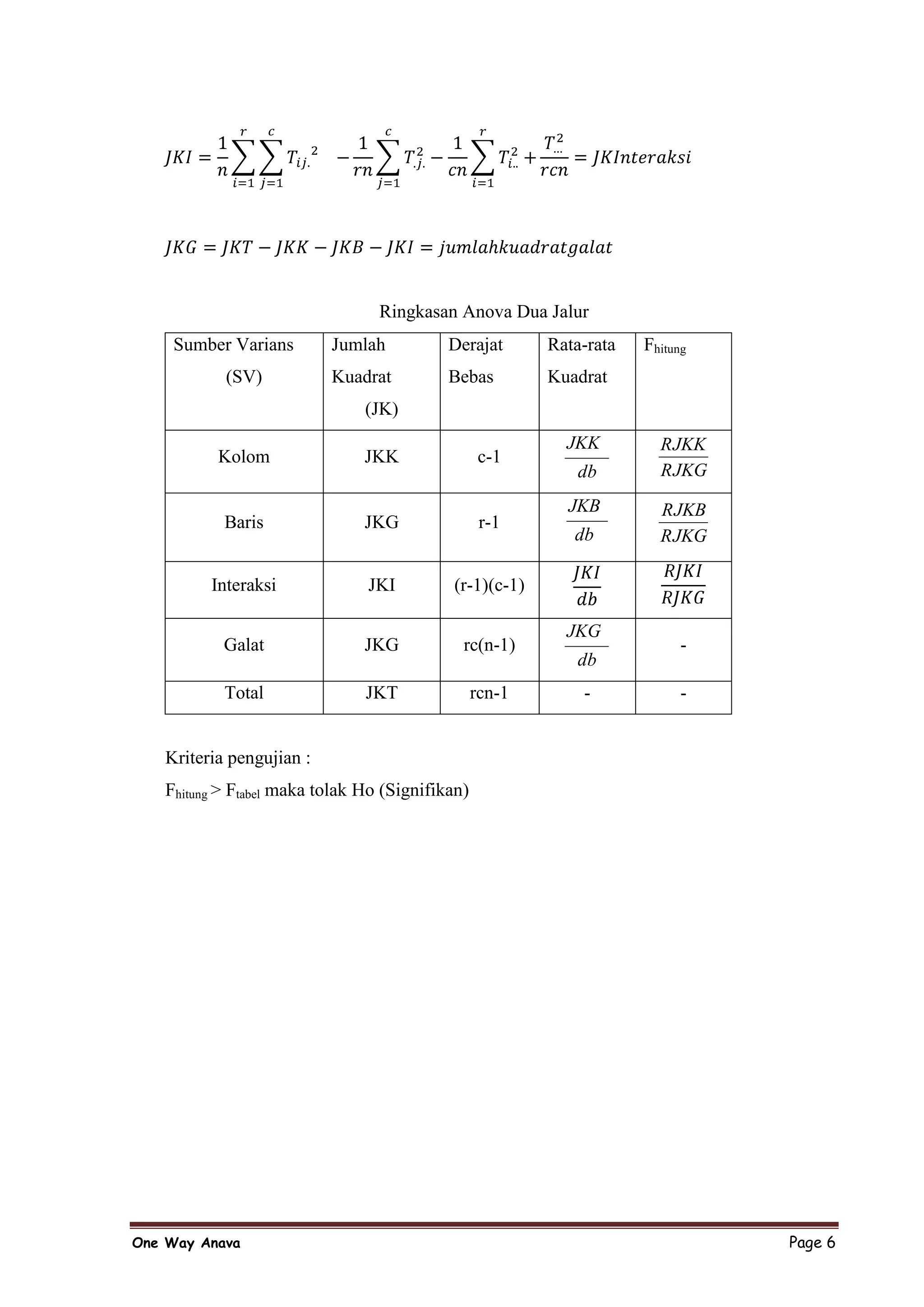
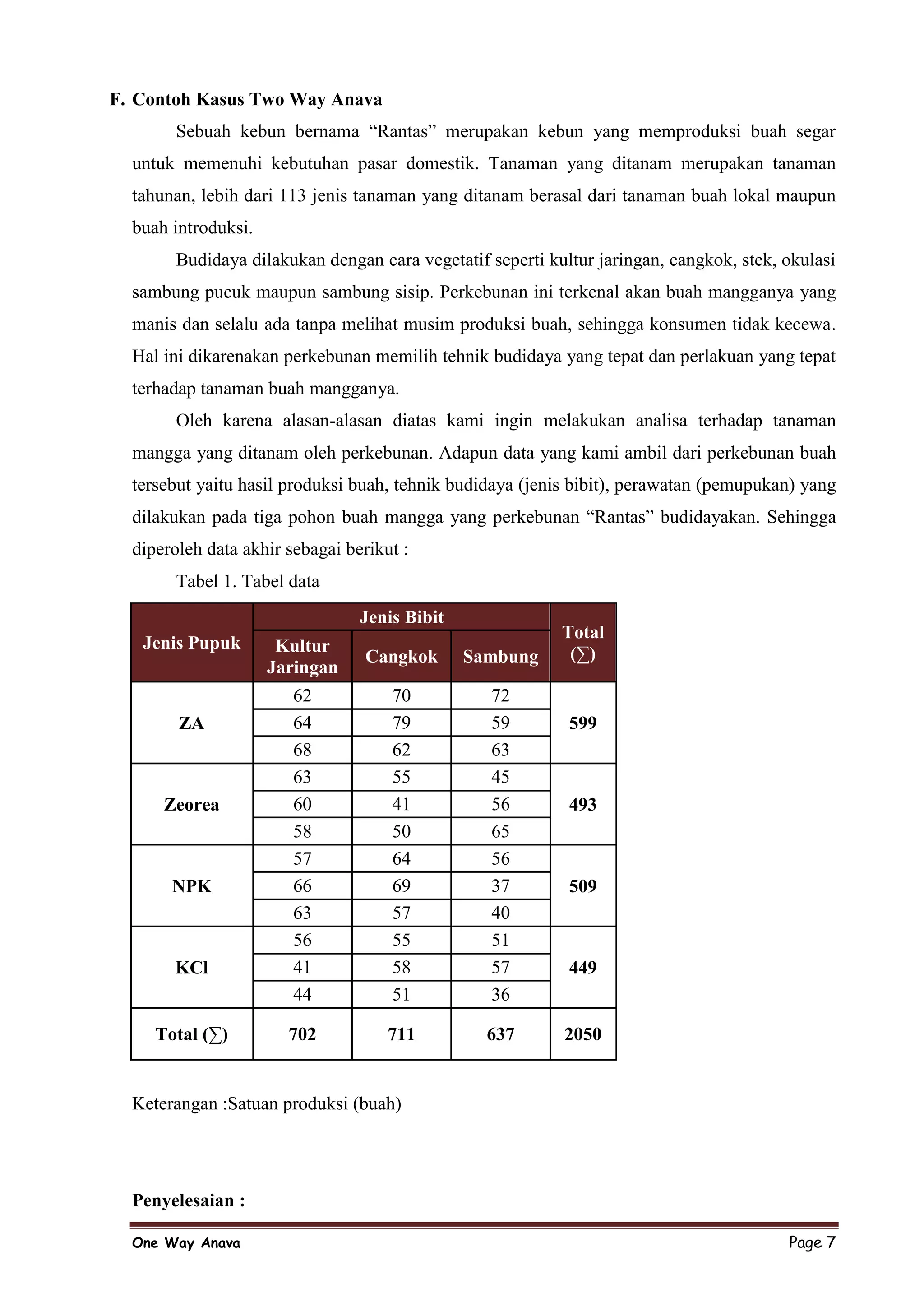
Ringkasan dokumen tersebut adalah: Dokumen tersebut membahas analisis ragam dua arah (two way ANOVA) untuk menguji perbedaan rata-rata hasil produksi buah mangga yang dipengaruhi oleh tiga jenis pupuk dan tiga jenis bibit tanaman. Hasilnya menunjukkan ada perbedaan signifikan antara rata-rata hasil produksi ketiga jenis pupuk, tetapi tidak untuk jenis bibit atau interaksinya.

1. MAKALAH STATISTIKA
TWO WAY ANAVA
Disusun Oleh :
KELOMPOK 3
FERI CHANDRA NIM : 201111004
IRMAN NIM : 201111016
HENDRA YOGI A.R. NIM : 201111001
HUSNUL HIDAYAT NIM : 201111031
WAHYU AKBAR A. NIM : 201111018
PROGRAM STUDI
BUDIDAYA PERKEBUNAN KELAPA SAWIT
POLITEKNIK KELAPA SAWIT CITRA WIDYA EDUKASI
2012

2. TWO WAY ANAVA
A. Pengertian
Analisis ragam atau analysis of variance (anava) adalah suatu metode untuk
menguraikan keragaman total data menjadi komponen-komponen yang mengukur berbagai
sumber keragaman. Secara aplikatif, anava digunakan untuk menguji rata-rata lebih dari dua
sampel berbeda secara signifikan atau tidak.
Two way anava merupakan pengujian hipotesis komparatif untuk data ordinal dari k
sampel (lebih dari dua sampel) yang berkorelasi. Two way anava dapat di bedakan atas dua,
yaitu two way anava tanpa Interaksi dan two way anava dengan interaksi. Dalam anava dua
jalur setiap variabel di bagi lagi ke dalam kelompok tertentu yang memiliki karakteristik
khusus. Dengan demikian, akan ada kluster-kluster yang lebih kecil dari setiap variabel.
B. Tujuan
1. Untuk mengetahui dan memahami uji statistik dengan menggunakan anava, terutama
anavadua arah.
2. Untuk mengetahui persoalan dan masalah-masalah yang berkaitan dengan uji anavadua
arah dalam kehidupan sehari-hari.
3. Agar dapat menyelesaikan persoalan uji anavadua arah dan menarik kesimpulan yang
sesuai dengan persoalan yang diujikan.
C. Jenis Varians
1. Varians Sistematik
Varians sistematik adalah variasi pengukuran karena adanya pengaruh alami atau buatan
manusia yang menyebabkan terjadinya peristiwa dapat diduga atau diramalkan dalam
arah tertentu. Misalnya seorang anak yang memperoleh makanan cukup bergizi secara
sistematik akan mempengaruhi pertumbuhan yang lebih baik dibandingkan anak
kekurangan gizi.salah satu varians sistematik adalah varians antar kelompok atau varians
eksperimental. varians ini menggambarkan adanya perbedaan atau variasi sistematik
antara kelompok-kelompok hasil pengukuran.
2. Varians Galat
Varians galat adalah varians yang terdapat di dalam kelompok data. digunakan untuk
menganalisis dua atau beberapa perlakuan/percobaan terhadap suatu obyek.
One Way Anava Page 2

3. D. Asumsi Dasar Anava
1. Kenormalan
Setiap harga dalam sampel berasal dari distribusi normal, sehingga distribusi skor sampel
dalam kelompok pun hendaknya normal. Kenormalan dapat diatasi dengan
memperbanyak sampel dalam kelompok, karena semakin banyak n maka distribusi akan
mendekati normal. Apabila sampel tiap kelompok kecil dan tidak dapat pula diatasi
dengan jalan melakukan transformasi.
2. Kesamaan Variansi
Masing-masing kelompok hendaknya berasal dari populasi yang mempunyai variansi
yang sama. Untuk sampel yang sama pada setiap kelompok, kesamaan variansi dapat
diabaikan. Tetapi, jika banyaknya sampel pada masing-masimg kelompok tidak sama,
maka kesamaan variansi populasi memang sangat diperlukan.
3. Penamatan Bebas
Sampel hendaknya diambil secara acak (random), sehingga setiap pengamatan
merupakan informasi yang bebas.
E. Analisis Two Anava
Dalam penyelesaian kasus two way anava ini, terdapat dua metode yang digunakan
yaitu two way anava tanpa interaksi dan two way anava dengan interaksi.
1. Analisis Two Way Anava Tanpa Interaksi
Sejumlah pengamatan dapat diklasifikasikan menurut dua kriteria dengan
menyusun data tersebut dalam baris dan kolom.
Kolom
Baris 1 2 ... j ... c
1 x11 x12 x1j x1c T1.
2 x21 x22 x2j x2c T2.
. . . . .
i . . . .
. . . . .
r xr1 xr2 xrj xrc Tr.
Total T.1 T.2 T.j T.c T..
One Way Anava Page 3

4. Dengan rumus JK sebagai berikut:
Ringkasan Anova Dua Jalur
Sumber Varians Jumlah Derajat Rata-rata Fhitung
(SV) Kuadrat Bebas Kuadrat
(JK)
JKK RJKK
Kolom JKK c-1
db RJKG
JKB RJKB
Baris JKB r-1
db RJKG
JKG
Galat JKG (r-1)(c-1) -
db
Total JKT rc-1 - -
Kriteria pengujian :
Fhitung > Ftabel maka tolak Ho (Signifikan)
One Way Anava Page 4

5. 2. Analisa Varian Dua Jalur dengan Interaksi
Sejumlah pengamatan dapat diklasifikasikan menurut dua kriteria dengan
menyusun data tersebut dalam baris dan kolom. Jika digunakan replikasi, maka didapat
tabel sebagai berikut:
kolom
Baris 1 2 ... ... ... c
1 x111 x121 . x1c1 T1..
x112 x122 . x1c2
. . . .
. . . .
. . . .
x11n x12n x1cn
. . . .
. . . .
. . . .
r.. xr11 xr21 xrc1 Tr..
xr12 xr22 xrc2
. . .
. . .
. . .
xr1n xr2n xrcn
Total T.1. T.2. T.c. T...
Dengan rumus JK sebagai berikut:
One Way Anava Page 5

6. Ringkasan Anova Dua Jalur
Sumber Varians Jumlah Derajat Rata-rata Fhitung
(SV) Kuadrat Bebas Kuadrat
(JK)
JKK RJKK
Kolom JKK c-1
db RJKG
JKB RJKB
Baris JKG r-1
db RJKG
Interaksi JKI (r-1)(c-1)
JKG
Galat JKG rc(n-1) -
db
Total JKT rcn-1 - -
Kriteria pengujian :
Fhitung > Ftabel maka tolak Ho (Signifikan)
One Way Anava Page 6

7. F. Contoh Kasus Two Way Anava
Sebuah kebun bernama “Rantas” merupakan kebun yang memproduksi buah segar
untuk memenuhi kebutuhan pasar domestik. Tanaman yang ditanam merupakan tanaman
tahunan, lebih dari 113 jenis tanaman yang ditanam berasal dari tanaman buah lokal maupun
buah introduksi.
Budidaya dilakukan dengan cara vegetatif seperti kultur jaringan, cangkok, stek, okulasi
sambung pucuk maupun sambung sisip. Perkebunan ini terkenal akan buah mangganya yang
manis dan selalu ada tanpa melihat musim produksi buah, sehingga konsumen tidak kecewa.
Hal ini dikarenakan perkebunan memilih tehnik budidaya yang tepat dan perlakuan yang tepat
terhadap tanaman buah mangganya.
Oleh karena alasan-alasan diatas kami ingin melakukan analisa terhadap tanaman
mangga yang ditanam oleh perkebunan. Adapun data yang kami ambil dari perkebunan buah
tersebut yaitu hasil produksi buah, tehnik budidaya (jenis bibit), perawatan (pemupukan) yang
dilakukan pada tiga pohon buah mangga yang perkebunan “Rantas” budidayakan. Sehingga
diperoleh data akhir sebagai berikut :
Tabel 1. Tabel data
Jenis Bibit
Total
Jenis Pupuk Kultur
Cangkok Sambung (∑)
Jaringan
62 70 72
ZA 64 79 59 599
68 62 63
63 55 45
Zeorea 60 41 56 493
58 50 65
57 64 56
NPK 66 69 37 509
63 57 40
56 55 51
KCl 41 58 57 449
44 51 36
Total (∑) 702 711 637 2050
Keterangan :Satuan produksi (buah)
Penyelesaian :
One Way Anava Page 7

8. 1. Membuat Hipotesa
a. Ha : Terdapat perbedaan rata-rata produksi dari penggunaan bibit.
Ho : semua rata-rata bibit sama.
b. Ha : Terdapat perbedaan rata-rata produksi dari penggunaan pupuk.
Ho : semua rata-rata pupuk sama.
c. Ha : Terdapat perbedaan rata-rata interaksi antara pupuk dan bibit.
Ho : semua rata-rata interaksi sama
Taraf signifikan 5%
2. Menghitung JKT, JKB, JKK, JKI, dan JKG
a. Jumlah Kuadrat Total (JKT)
622+642+682+632+602+582+572+662+632+562+412+442+702+792+622+552+412+502+64
2
+692+572+552+582+512+722+592+632+452+562+652+562+372+402+512+572+362 –
2
(2050 :36)
= 3645,89
b. Jumlah Kuadrat Baris (JKB)
(5992+4932+5092+4492 : 9) – (20502:36)
= 118059,1 - 116736,1
= 1323
c. Jumlah Kuadrat Kolom (JKK)
(7022+7112+6372 : 12) – (20502:36)
= 117007,8– 116736,1
= 271,72
d. Jumlah Kuadrat Interaksi (JKI)
((1942+1812+1862+1412+2112+1462+1902+1642+1942+1662+1332+1442) : 3) –
118059,1 - 117007,8+ 116736,1
= 119108 -118059,1 - 117007,8+ 116736,1
= 777,2
e. Jumlah Kuadrat Galat (JKG)
3645,89- 271,72- 1323 - 777,2 = 1273,97
3. Mencari Nilai Fhitung
One Way Anava Page 8

9. Jumlah
Sumber Varians Derajat Rata-rata Fhitung
Kuadrat
(SV) Bebas Kuadrat
(JK)
Baris 1323 3 441 8,31
Kolom 271,72 2 135,86 2,56
Interaksi 777,2 6 128,7 2,42
Galat 1273,97 24 53,08 -
Total 3645,89 35 - -
4. Mencari Nilai Ftabel (5%)
a. Ftabel JKB = (3,24)  3,01
b. Ftabel JKK = (2,24)  3,40
c. Ftabel JKI = (6,24)  2,51
5. Menarik Kesimpulan
a. Kriteria Pengujian
Fhitung≤ Ftabel, maka tolak Ha dan terima H0 berarti tidak signifikan.
b. Kesimpulan
a. Fhitung≥ Ftabel, atau 8,31≥3,01 maka tolak H0 dan terima Ha(Terdapat perbedaan rata-
rata produksi dari penggunaan bibit)
b. Fhitung≤ Ftabel, atau 2,56≤3,40 maka tolak Ha dan terima H0(semua rata-rata pupuk
sama)
c. Fhitung≤ Ftabel, atau 2,42≤ 2,51 maka tolak Ha dan terima H0Terima Ho (semua rata-
rata interaksi sama)
Dari hasil kesimpulan menyatakan bahwa terdapat perbedaan rata-rata hasil produksi untuk
jika digunakan ketiga jenis pupuk, maka harus digunakan uji lanjut untuk mengetahui letak
perbedaannya.
6. Uji Wilayah Berganda
Untuk mengetahui nilai tengah mana saja yang berbeda nyata dapat digunakan Uji Wilayah
Berganda Duncan. rumusnya sebagai berikut :
One Way Anava Page 9

10. Rp :wilayah terstudentkan nyata terkecil.
7. Menghitung nilai rata-rata produksi masing-masing pupuk :
A = 702/12 = 58,50
B = 711/12 = 59,25
C = 637/12 = 53,08
Mengurutkan nilai rata-rata dari yang terkecil sampai yang terbesar :
53,08 58,50 59,25
Diketahui RJKG= 53,08 dengan db= 24 dan taraf signifikan 5%, sehingga dapat diringkas :
P 2 3 4 5
rp 2,919 3,066 3,160 3,226
Rp 6,14 6,44 6,64 6,77
Dengan membandingkan wilayah nyata terkecil itu dengan selisih rata-rata sampel yang
telah diurutkan didapat sebagai berikut :
1) maka tidak berbeda.
2) maka berarti B> C
3) maka berarti A> C
8. Kesimpulan, dari hasil analisis data diatas, terdapat 2 perbedaan rata-rata produksi buah
mangga dalam penerapan penggunaan bibit pada kebun “Rantas”.
Saran, untuk itu perlu dikaji lebih lanjut perbedaan produksi buah mangga tersebut, cari
produksi yang lebih baik dari perbedaan yang ada dan tanggapi lebih lanjut hal tersebut
sehingga dapat memperoleh hasil produksi yang maksimal.
DAFTAR PUSTAKA
One Way Anava Page 10

11. http://statistikpendidikanii.blogspot.com/2009/01/perbedaan-one-way-anava-dan-two-
way.html. Diakses pada tanggal 2 Juli 2011
http://www.pdf4me.net/pdf-data/anova-dua-jalur.phpDiakses pada tanggal 2 Juli 2011
http://kelompok7iiiastatistikadasar.blogspot.com/2009/11/anova.htmlDiakses pada tanggal
2 Juli 2011
One Way Anava Page 11