Downloaded 628 times
Uploaded byTorang Aritonang
Ppt anova k elompok 6
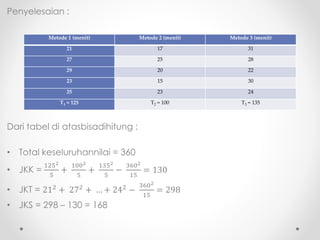
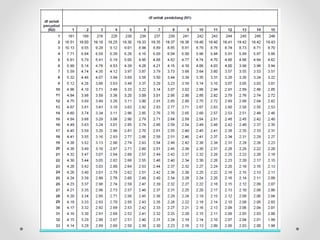
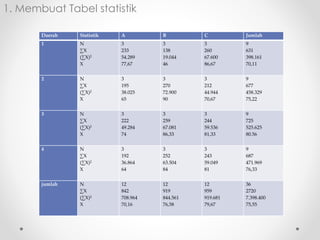
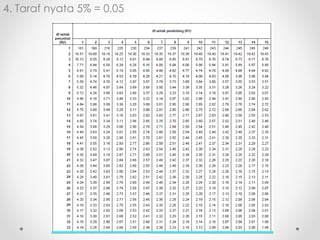
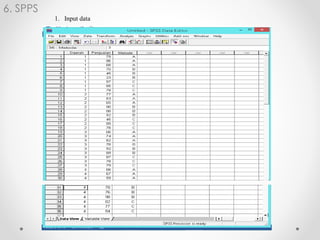
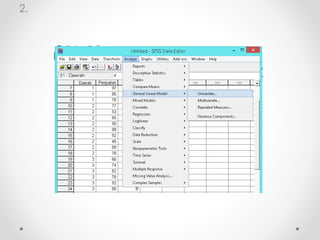
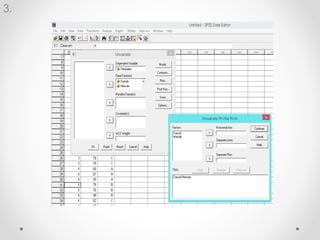
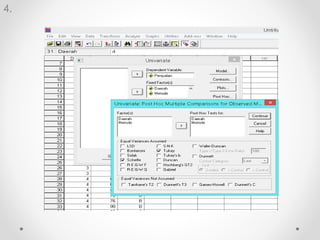
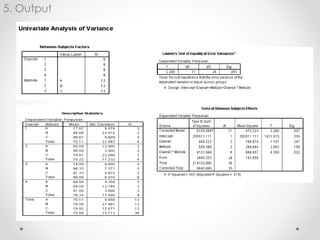
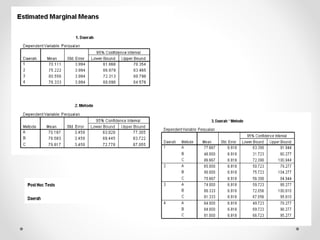
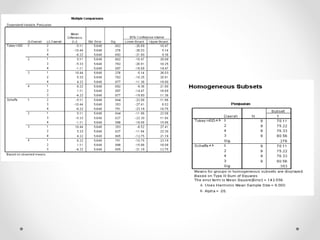
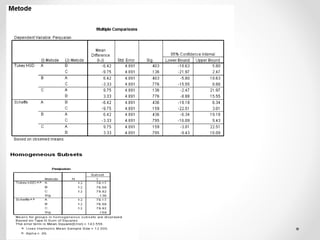
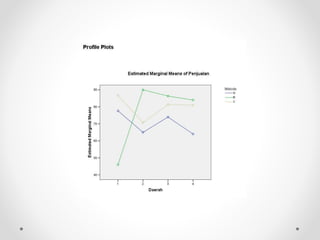
Dokumen ini membahas analisis varians (ANOVA), sebuah metode statistik untuk membandingkan ragam dari beberapa kelompok sampel. ANOVA digunakan untuk menguji pengaruh faktor-faktor tertentu terhadap variabel dependen dan memerlukan asumsi seperti normalitas dan homoskedastisitas. Contoh perhitungan dan analisis ANOVA satu arah dan dua arah juga dijelaskan, serta kesimpulan dari penelitian mengenai metode belajar terhadap prestasi siswa.
Ppt anova k elompok 6
- 1. ANALYSIS OF VARIANCE Kelompok4 Abrar Muharman 3334131932 Alfia Nurhasana 3334141268 Giana Trinovita 3334130282 Hery Robiyantoro 3334130512 M. Dimaz 3334140330 Mohammad Fajar 3334121980 Rifky Wijaya 3334130273 Tri Alif Shandy 3334130142
- 2. Anova Anova adalah suatumetode analisis statistika yang termasuk ke dalam cabang statistika inferensi. Disebut sebagai analisis ragam, karena dalam prosesnya ANOVA memilah-milah keragaman menurut sumber-sumber yang mungkin. Sumber keragaman inilah yang akan digunakan sebagai pembanding untuk mengetahui sumber mana yang menyebabkan terjadinya keragaman tersebut.
- 3. Beberapa asumsi yangharus dipenuhi pada uji Anova: • Sampel berasal dari kelompok yang independen • Data masing-masing kelompok berdistribusi normal • Varian antar kelompok harus homogen, dikenal sebagai homoskedastisitas • Komponen-komponen dalam modelnya bersifat aditif (saling menjumlah).
- 4. Uji hipotesis denganAnova digunakan, setidaknya karena beberapa alasan berikut: • Memudahkan analisa atas beberapa kelompok sampel yang berbeda dengan resiko kesalahan terkecil. • Mengetahui signifikansi perbedaan rata-rata (μ) antara kelompok sampel yang satu dengan yang lain. • Analisis varians relatif mudah dimodifikasi dan dapat dikembangkan untuk berbagai bentuk percobaan yang lebih rumit.
- 5. Contoh Perhitungan Anova 1. •Rata-rata keempatdata ∑𝑓𝑥 𝑛 = 75 + 71,25 + 77,5 + 68,75 4 = 73,125 • JumlahKuadrat-kuadrat(JK)(𝑥 − ∑𝑓𝑥 𝑛 )2= 75 − 73,125 2 + (71,25 − Produk A B C D Rata Rata 75 71,25 77.5 68,75
- 6. 2. • Rata-rata A ∑𝑓𝑥 𝑛 = 3,2+ 3,6 + 4,0 + 3,8 4 = 3,65 • Rata-rata B ∑𝑓𝑥 𝑛 = 2,5 + 2,9 + 2,4 + 3,0 4 = 2,7 • Rata-rata data 𝑋 = 4 3,65 + 4(2,7) 8 = 6,35 • JumlahKuadrat (JK) 𝐴 = 4 3,65 2 = 53,29 𝐵 = 4(2,7)2 = 29,16 • JK dikoreksi 53,29 + 29,16 = 82,45 • Variansi 𝐽𝐾 𝑑𝑖𝑘𝑜𝑟𝑒𝑘𝑠𝑖 𝐷𝑒𝑟𝑎𝑗𝑎𝑡 𝐾𝑒𝑏𝑒𝑏𝑎𝑠 = 82,45 3 = 27,48 Baja A 3,2 3,6 4,0 3,8 Baja B 2,5 2,9 2,4 3,0
- 7. Anova satu arah Anovasatu arah digunakan ketika variabel dependen-nya univariat dengan pengaruh satu faktor. Maksud dari kasus ini yaitu untuk menguji perbedaan rata-rata lebih dari dua sampel dimana dalam melakukan analisis hanya bisa satu arah.
- 8. Asumsi-asumsi anova satuarah : • Populasi yang akan diuji berdistribusi normal. • Varians dari populasi-populasi tersebut adalah • sama. • Sampel tidak berhubungan satu dengan yang lain.
- 9. Contoh Perhitungan Anova1 arah Metode 1 (menit) Metode 2 (menit) Metode 3 (menit) 21 17 31 27 25 28 29 20 22 23 15 30 25 23 24 Sebuah penelitian dilakukan untuk mengetahui apakah ada pengaruh perbedaan metode belajar pada tingkat prestasi siswa. Ada tiga metode belajar yang akan diuji. Diambil sampel masing-masing 5 guru untuk mengerjakan pekerjaannya, lalu dicata waktu yang digunakan (menit) sebagai berikut: Ujilah dengan α = 0,05 apakah ada pengaruh perbedaan metode belajar pada waktu yang digunakan?
- 10. Penyelesaian : Dari tabeldi atasbisadihitung : • Total keseluruhannilai = 360 • JKK = 1252 5 + 1002 5 + 1352 5 − 3602 15 = 130 • JKT = 212 + 272 + … + 242 − 3602 15 = 298 • JKS = 298 – 130 = 168 Metode 1 (menit) Metode 2 (menit) Metode 3 (menit) 21 17 31 27 25 28 29 20 22 23 15 30 25 23 24 T1 = 125 T2 = 100 T3 = 135
- 12. Tabel Anova • PengujianHipotesis 𝐻0 = 𝜇1 = 𝜇2 = ⋯ = 𝜇 𝑘 𝐻 𝑎 : Tidak semuanya sama(𝑠𝑒𝑡𝑖𝑑𝑎𝑘𝑛𝑦𝑎 𝑎𝑑𝑎 𝜇𝑖 ≠ 𝜇 𝑗 𝑢𝑛𝑡𝑢𝑘 𝑖 ≠ 𝑗) • Statistik Uji = Fhitung = 4,64 • Karena Fhitung> Ftabel maka tolak Ho • Kesimpulan: Ada pengaruh perbedaan metode kerja pada waktu yang digunakan. Sumber Derajat Jumlah Varian Fhitung Ftabel Keragaman Bebas Kuadrat (Ragam) AntarKolom 2 130 65 4,64 F(2,12) = 3,89 Sisaan 12 168 14 14 298
- 13.
- 15. Anova 2 arah Anovadua arah mempertimbangkan 2 faktor yang mengakibatkan terjadinya penyimpangan (dispersi) dan nilai-nilai yang dihitung dengan standar deviasi atau varians. Apabila design yang dikembangkan untuk mencari ada tidaknya perbedaan dari 2 variabel bebas, dan masing-masing variable bebas dibagi dalam beberapa kelompok, maka design yang dikembangkan tersebut sering disebut dengan Anova dua arah.
- 16. Ada beberapa asumsiyang dipakai dalam Anova dua arah : • Setiap skor dalam sel harus berdistribusi normal. Asumsi ini dapat sedikit diabaikan jika sample tiap sel cukup banyak . • Variasi Skor pada setiap sel hendaknya homogen atau sama • Skor yang ada bebas dari pengaruh variable yang tidak teliti.
- 17. Contoh soal :Berikutini merupakan contoh kasus dalam bidang pemasaran, apakah daerah dan metode pemasaran mempunyai hubungan dengan jumlah hasil penjualan. Metode A B C Daerah 1 79 23 85 86 45 97 68 70 78 2 53 90 45 77 92 78 65 88 89 3 66 89 79 74 78 87 82 92 78 4 67 98 82 66 78 77 59 76 84
- 18. 1. Membuat Tabelstatistik Daerah Statistik A B C Jumlah 1 N ∑X (∑X)2 X 3 233 54.289 77,67 3 138 19.044 46 3 260 67.600 86,67 9 631 398.161 70,11 2 N ∑X (∑X)2 X 3 195 38.025 65 3 270 72.900 90 3 212 44.944 70,67 9 677 458.329 75,22 3 N ∑X (∑X)2 X 3 222 49.284 74 3 259 67.081 86,33 3 244 59.536 81,33 9 725 525.625 80.56 4 N ∑X (∑X)2 X 3 192 36.864 64 3 252 63.504 84 3 243 59.049 81 9 687 471.969 76,33 jumlah N ∑X (∑X)2 X 12 842 708.964 70,16 12 919 844.561 76,58 12 959 919.681 79,67 36 2720 7.398.400 75,55
- 19. 2. Membuat tabelRumus Unsur Persiapan Anova Sumbe r Variasi Jumlah Kuadrat Derajat bebas Rata-rata kuadrat Fo Rata- rata Baris Rata- Rata Kolom Interak si 𝐽𝐾𝐵 = 398.161 + 458.329 + 525.625 + 471.696 9 − 7.398.400 36 = 498,222 𝐽𝐾𝐾 = 708.964 + 844.561 + 919.681 12 − 7.398.400 36 = 589,389 JK 𝐵𝐾 = ∑ (∑𝑋 𝐵 )2 𝑛 𝐵 – (∑𝑋 𝑇 )2 𝑁 – JKB – JKK = (54.289 + 19.044 + 67.600 + 38.025 + 72.900 + 44.944 + 49.284 + 67.081 + 59.536 + 36.864 + 63.504 + 59.049)/3 − 7.398.400 36 − 498,222 − 589,389 =4107,944 𝑏 − 1 = 4 − 1 = 3 𝑘 − 1 = 3 − 1 = 2 ( 𝑏 − 1)( 𝑘 − 1) = 3𝑥2 = 6 𝑆1 = JK 𝐵 𝑑𝑏 𝐵 = 498.22 3 = 166,047 𝑆2 = JK 𝐾 𝑑𝑏 𝐾 = 589,389 2 = 294,694 𝑆3 = JK 𝐵𝐾 𝑑𝑏 𝐵𝐾 = 4107,944 6 = 684,657 𝑓1 = 𝑆1 𝑆4 = 166,047 143,556 = 1,1566 𝑓1 = 𝑆2 𝑆4 = 294,694 143,556 = 2,052 𝑓1 = 𝑆3 𝑆4 = 684,657 143,556 = 4,769 Total (T) Error JKT = ∑(𝑋 𝑇)2 - (∑𝑋 𝑇)2 𝑁 == (79)2 + (86)2 + ⋯ … + (77)2(84)2 − 7.398.400 36 = 8640,889 JKE = JKT − JKB − JKK − JK 𝐵𝐾 = 8640,889 − 498,222 − 589,389 − 4107,944 = 3445,334 𝑛 − 1 = 36 − 1 = 35 ( 𝑛 − 𝑏𝑘) = 36 − 4.3 = 24 𝑆4 = JK 𝐸 𝑑𝑏 𝐸 = 3445,334 24 = 143,556
- 20. 3. Hipotesis • 𝑓1:𝐻0 ′ = ∝1 = ∝2= ∝3= ∝4= 0 𝐻1 ′ = 𝑠𝑒𝑘𝑢𝑟𝑎𝑛𝑔 − 𝑘𝑢𝑟𝑎𝑛𝑔𝑛𝑦𝑎 𝑎𝑑𝑎 𝑠𝑎𝑡𝑢 𝛼1 ≠ 0 • 𝑓2: 𝐻0 ′′ = 𝛽1 = 𝛽2 = 𝛽3 = 𝛽4 = 0 𝐻1 ′′ = 𝑠𝑒𝑘𝑢𝑟𝑎𝑛𝑔 − 𝑘𝑢𝑟𝑎𝑛𝑔𝑛𝑦𝑎 𝑎𝑑𝑎 𝑠𝑎𝑡𝑢 𝛽𝑗 ≠ 0 • 𝑓3: 𝐻0 ′′′ = (∝ 𝛽)11 = (∝ 𝛽)12= (∝ 𝛽)13= ⋯ = (∝ 𝛽)43= 0 𝐻′1 ′′ = 𝑠𝑒𝑘𝑢𝑟𝑎𝑛𝑔 − 𝑘𝑢𝑟𝑎𝑛𝑔𝑛𝑦𝑎 𝑎𝑑𝑎 𝑠𝑎𝑡𝑢 (∝ 𝛽)𝑖𝑗 ≠ 0
- 21. 4. Taraf nyata5% = 0,05
- 22. • 𝑓1 >𝑓∝ 𝑏−1;𝑏𝑘 𝑛−1 • 𝑓1 > 𝑓0,05 4−1;4(3)2 • 𝑓1 > 𝑓0,05 3;24 • 𝑓1 > 3,01 → 𝐻0 ′ 𝑑𝑖𝑡𝑜𝑙𝑎𝑘 • 𝑓2 > 𝑓∝ 𝑘−1;𝑏𝑘 𝑛−1 • 𝑓2 > 𝑓0,05 3−1;4(3)2 • 𝑓2 > 𝑓0,05 2;24 • 𝑓2 > 3,40 → 𝐻0 ′′ 𝑑𝑖𝑡𝑜𝑙𝑎𝑘 • 𝑓3 > 𝑓∝ 𝑏−1 (𝑘−1);𝑏𝑘 𝑛−1 • 𝑓3 > 𝑓0,05 4−1 (3−1);4(3)2 • 𝑓3 > 𝑓0,05 6;24 • 𝑓3 > 2,51 → 𝐻0 ′′′ 𝑑𝑖𝑡𝑜𝑙𝑎𝑘 • 𝑓1 = 𝑆1 𝑆4 = 166,047 143,556 = 1,1566 < 𝑓1𝑡𝑎𝑏 𝑚𝑎𝑘𝑎 𝐻0 ′ 𝑑𝑖𝑡𝑒𝑟𝑖𝑚𝑎 • 𝑓2 = 𝑆2 𝑆4 = 294,694 143,556 = 2,052 < 𝑓2𝑡𝑎𝑏 𝑚𝑎𝑘𝑎 𝐻0 ′′ 𝑑𝑖𝑡𝑒𝑟𝑖𝑚𝑎 • 𝑓3 = 𝑆3 𝑆4 = 684,657 143,556 = 4,769 > 𝑓3𝑡𝑎𝑏 𝑚𝑎𝑘𝑎 𝐻0 ′ 𝑑𝑖𝑡𝑜𝑙𝑎𝑘
- 23. 5. Kesimpulan Metode penjualansecara siginifikan tidak berpengaruh terhadap penjualan produk , begitu juga dengan daerah penjualan yg cukup berpengaruh pada penjualan produk, tetapi tidak terjadi interaksi antara daerah dan metode penjualan.
- 24. 6. SPPS 1. Inputdata
- 25.
- 26.
- 27.
- 28.
- 33.